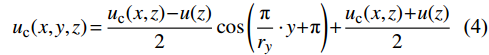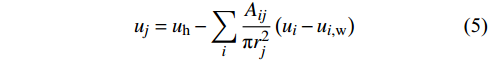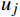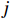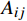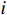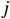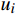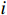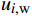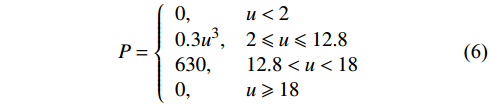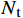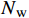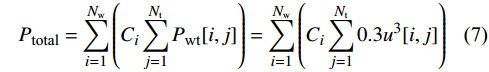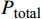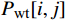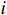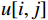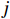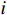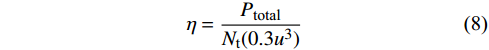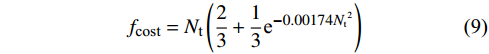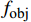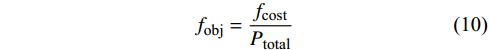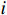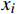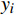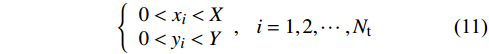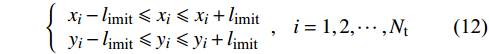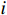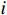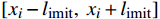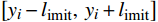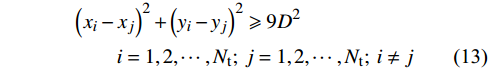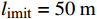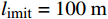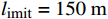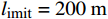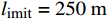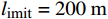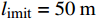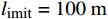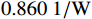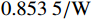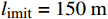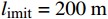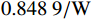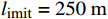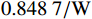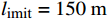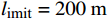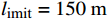Hierarchical wind farm layout optimization considering different constraint conditions
-
摘要:
为了提高风电场布局优化中尾流模型预测精度,以便能够较好预测风机安装台数和最大限度降低度电成本,本文基于改进三维尾流模型,考虑风力机处于不同约束区间,采用分级优化策略对2 km × 2 km风电场进行精确布局优化。首先,利用网格法对风电场进行第一阶优化;其次,考虑不同约束区间,采用坐标法对第一级优化结果进行第二阶优化。研究表明:与Jensen尾流模型相比,改进后的三维尾流模型可以更合理地优化风电场布局;考虑收敛速度及度电成本,当约束区域为limit = 150、200 m时,第二阶算法迭代速度较快,优化后其度电成本为0.8498/W,相比第一阶优化结果,降低了3.33%。
Abstract:Low prediction accuracy of wake model for wind farm layout and the impact of different constraint regions on the optimization results hinder the accurate prediction of the wind turbine number and minimize the energy cost. Based on an improved 3D wake model, a 2 km × 2 km wind farm layout is optimized using a hierarchical optimization strategy by taking different constraint conditions into account. The coordinate method is used to perform the second-order optimization on the first-order optimization results obtained by the grid method. It is shown that compared to the Jensen wake model, an improved 3D wake model is more reasonable to optimize the wind farm layout. Considering the convergence speed and the power cost, when the constraint interval is
limit=150and200m , the second-order algorithm has a faster iterative speed, and the power cost is 0.8498/W, which is 3.33% lower than the first-order optimization. The optimized layout shield light on the wind turbines installation.-
Keywords:
- wind farm layout /
- constraint regions /
- improved wake model /
- hierarchical optimization /
- power cost /
- wind turbine
-
0. 引 言
风电场的微观布局优化是指确定某一风电场区域内风力机的最佳安装位置,以减小风力机之间的干扰,并尽可能多地捕获风能。在风电场布局的优化过程中,上游风力机尾流将会对下游风力机的能量捕获造成影响,因此,准确预测尾流风速至关重要。Jensen尾流模型[1]是一种经典的半经验尾流模型,目前已得到了广泛的应用。Tao等[2]提出了一种新的三维高斯尾流模型,并将其应用于风电场布局,结果表明,该方法能够对其进行高效而合理的优化。宋翌蕾等[3]提出的三维尾流模型考虑了来流风切变效应的影响,并在多组地表粗糙度情况下验证了该模型的准确性。汪泉等[4]修正了风切变效应对尾流区域速度分布的影响,由此提出了一种改进的三维尾流模型,并通过风洞实验数据验证了所提模型的准确性。
风电场布局优化往往以度电成本极小和风电场总功率极大为目标。Grady等[5]利用遗传算法优化风电场的微观布局,采用Jensen尾流模型模拟风电场中上游风力机的尾流效应,并根据预安装机组的机型特征计算得到了风电场的总发电量。Long等 [6]提出了一种数据驱动的进化算法,在保持解性能的同时可以减少计算时间。Lei 等[7]提出了一种具有自适应策略的粒子群优化方法,并用于优化风电场布局。结果表明:在安装有25台风机的风电场中,所提出的方法在4种风况下获得的最佳平均转换效率分别为89.92%、92.90%、95.39%和90.75%。Wang[8] 针对同一风电场,分别采用网格法和坐标法进行风电场布局优化,发现采用坐标法得到的布局,其能量输出要比网格法好。Yang和Najafi[9]采用启发式-梯度算法对风电场布局进行多阶段优化,结果表明:对于离散化-连续多阶段模型,采用该方法其年均发电量可以提高6.20%。蒋秋俊等[10]基于网格-坐标法采用一维尾流模型对2 km × 2 km的标准风电场进行风力机布局优化,随后,将其应用到不规则的实际风电场中,并对第二次优化的约束区间进行了研究,结果表明,所提出的方法可有效提高总发电量。徐佳楠等[11]提出了一种自适应权重的遗传-粒子群优化算法,结果表明:运用此改进算法优化后的风电场单位发电成本为2016元,相比优化前减少了232元;年发电量为
8.26×104 kW⋅ h,比优化前提高了8.54×103 kW⋅ h;此外,尾流损失减少了1.12%。张子良等[12]提出了一种几何约束条件下海上风电场智能布局优化方法,结果表明,相比于原始布局方案,考虑海缆铺设成本增加的布局优化方案可将风电场年发电量提升2.13%~2.64%。此外,还有学者[13-15]在风电场布局优化问题上做出了卓有成效的研究工作。然而,上述研究大都是对优化算法进行改进或就网格法与坐标法的优缺点进行对比。虽然部分风电场布局优化也采用了网格法-坐标法这一分阶段优化方法,但是利用改进三维尾流模型来预测尾流风速并考虑不同约束优化区间的风电场分级优化策略鲜有相关报道。本文采用改进三维尾流模型来预测尾流风速,考虑了不同约束区间对优化结果的影响,利用两级优化策略对2 km×2 km风电场布局进行分级优化。首先,利用网格法进行第一级优化,确定风电场的风力机数量,并与Jensen尾流模型优化结果进行对比分析,以验证该改进模型在风电场布局优化的准确性。其次,考虑不同约束区间,利用坐标法进行第二级精确优化,考虑优化度电成本及收敛效率,从而确定更加精准的风电机组布局位置。
1. 改进三维尾流模型
在一维Jensen尾流模型的基础上,建立了二维Jensen尾流模型[1],其表达式如下:
风速预测步:u∗=uh[1−2a(1+kwakex/xr1r1)2] (1) 风速校正步:uc∗(x,z)=(uh−u∗)cos(πrzr+π)+u∗ (2) 式中:uh为风机入流风速;r1为初始尾流半径,
r1=rd√(1−a)/(1−2a) ,rd为风轮半径,a为轴向因子,a=(1−√1−CT)/2 ,CT为风力机推力系数;kwake为尾流扩张系数;x为风力机下游尾流区域与风力机之间的距离;rz为风力机下游x位置处的尾流区域半径。二维Jensen尾流模型没有考虑来流风切变的影响,而来流风切变将会影响风力机垂直方向的速度分布,如图1所示。三维尾流模型用风切变函数来表达入流风速特性,如式(3)所示:
u(z)=uref(zzref)α (3) 式中:
zref 为风力机参考高度;uref 为参考高度处的入流风速;α 为风切变系数。在考虑来流的风切变情况下,改进三维尾流模型表达式如下:
uc(x,y,z)=uc(x,z)−u(z)2cos(πry⋅y+π)+uc(x,z)+u(z)2 (4) 式中:uc(x, z)为风机尾流在垂直方向上的速度分布,u(z)为风速恢复到受风切变效应影响的来流风速,ry为水平方向上尾流区域半径。
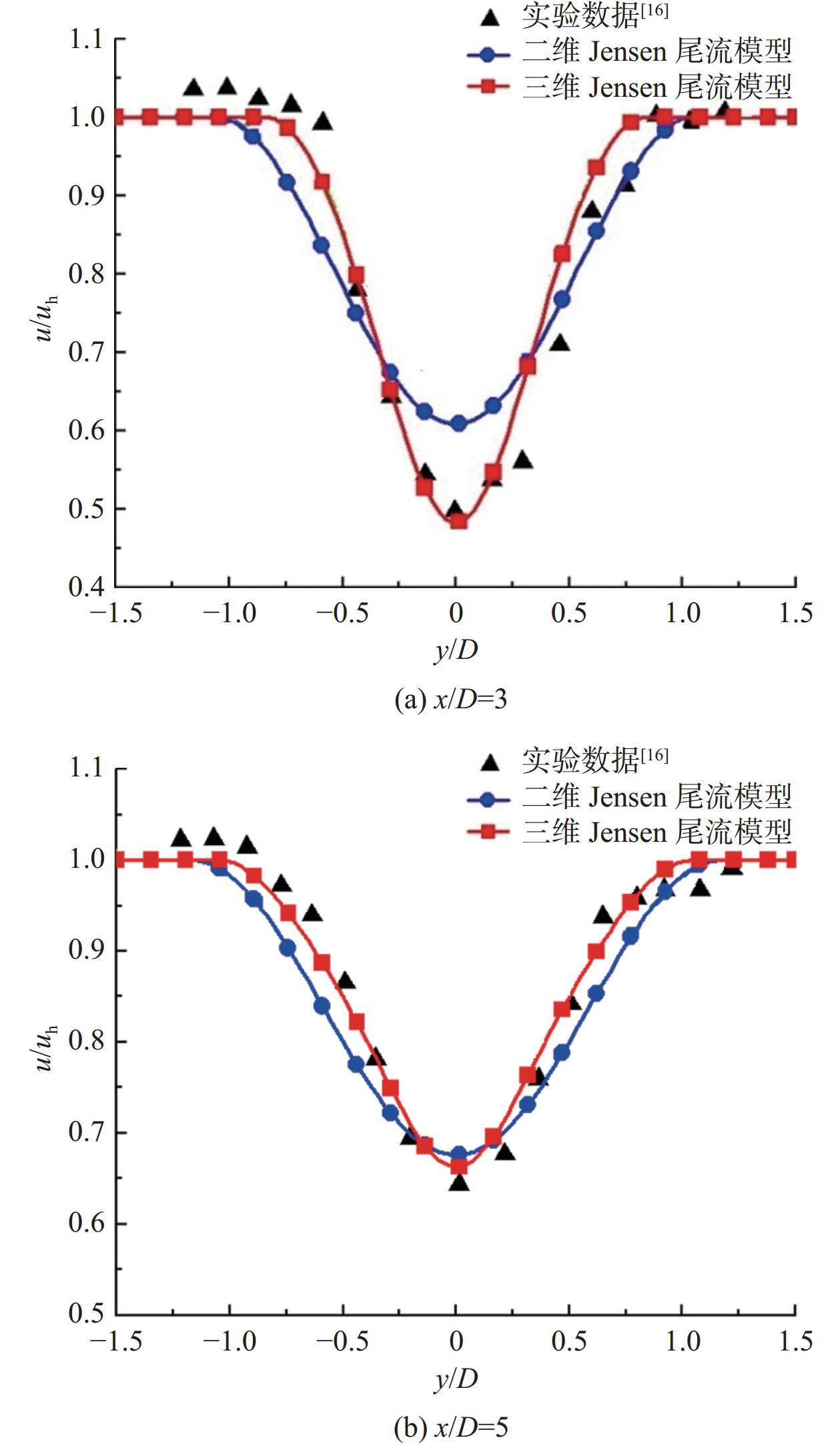
为了比较三维尾流模型与二维尾流模型对计算结果的影响,本文根据Gao等[16]的研究数据,选取轮毂高度处的来流风速10.4 m/s、湍流强度14%、风力机推力系数0.68为计算条件,根据式(1)和(3)分别计算了二维尾流模型和三维尾流模型的速度分布,如图2所示。通过与文献[16]实验数据对比可知:在x/D = 3位置处(D为风轮直径),三维尾流模型较好地描述了尾流区域速度分布,而二维尾流模型明显高估了尾流的恢复速度;在x/D = 5位置处,三维尾流模型的速度分布与实验数据更加吻合,表明了该三维尾流模型的合理性。
2. 风电场布局优化问题及目标函数
2.1 布局优化中的问题描述
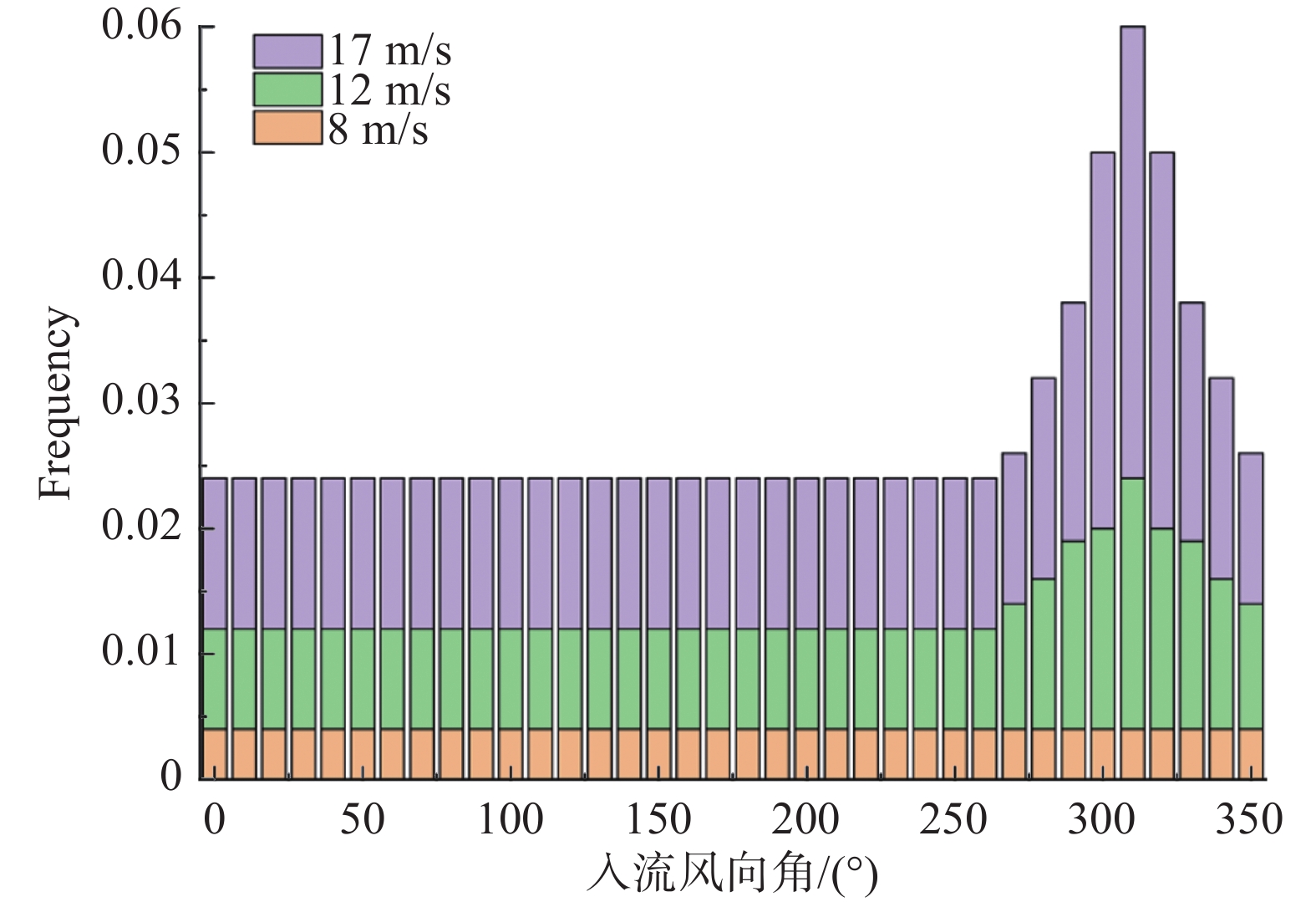
本文对目标风电场进行微观布局优化设计,为了便于对比,采用与Grady等[5]提出的相同的物理模型。优化的目标风电场为2 km × 2 km的平坦地形,风力机具体参数如表1所示,同时考虑变风速变风向工况,其3种不同风速情况下的风资源分布如图3所示,其中,纵坐标表示入流风的频率,入流风速分别为8、12、17 m/s,并将入流风向离散为36个风向,每个风向角间隔10°,作为横坐标,并假设各风向发生的概率相等。
表 1 风电场及风力机参数Table 1. Caculating parameters of wind turbine and wind farms参数 值 风轮直径d/m 40 推力系数CT 0.88 轮毂高度h/m 60 切入风速/(m·s–1) 2 切出风速/(m·s–1) 18 风电场的表面粗糙度z0/m 0.3 2.2 风电场尾流模型叠加
尾流叠加模型是将单个风力机的尾流速度与来流风速进行组合。大型风电场中风力机可能会受多个上游风力机的尾流干扰,因此,在计算风电场整体功率时,需考虑尾流叠加效应。本文引入尾流叠加计算公式[17],以确定下游风机的入流速度,如式(5)所示:
uj=uh−∑iAijπr2j(ui−ui,w) (5) 式中:
uj 为下游风力机j 感应到的平均风速,Aij 为上游风力机i 的尾流区域对下游风力机j 转子的遮挡面积,rj为下游风力机j在水平方向上的尾流区域半径,ui 为上游风力机i 处的平均风速,ui,w 为上游风力机i 在下游风力机j 处的平均尾流风速。2.3 目标函数的构建
假设本文研究的目标风电场中只存在一种风力机,其功率计算公式如式(6)所示:
P={0,u<20.3u3,2⩽ (6) 式中u为风力机的平均风速,m/s。当风速低于2 m/s时,入流风速低于风力机的启动风速,此时功率为0;当风速处于2 m/s到12.8 m/s之间时,入流风速与风力机的输出功率为幂函数关系;当风速处于12.8 m/s到18 m/s之间时,风力机的输出功率为630 kW。当风速高于18 m/s时,入流风速高于切出风速,风力机停止工作。
为了便于对比,将1 h风力机的输出功率作为单位输出功率。若风电场中存在
N\mathrm{_{t\mathrm{ }}} 台预安装的风力机,风资源含有N\mathrm{_w} 个风向,则风电场的总功率为:{P_{{\text{total}}}} = \sum\limits_{i = 1}^{{N_{\text{w}}}} {\left(C_i\sum\limits_{j = 1}^{{N_{\text{t}}}} {{P_{{\text{wt}}}}[i,j]} \right)} = \sum\limits_{i = 1}^{{N_{\text{w}}}} {\left(C_i\sum\limits_{j = 1}^{{N_{\text{t}}}} {0.3{u^3}[i,j]} \right)} (7) 式中:
{P_{{\text{total}}}} 为风电场总的单位输出功率,{P_{{\text{wt}}}}[i,j] 为第j台风力机在第i 个风向中的输出功率,u[i,j] 为第j 台风力机在第i 个风向中的平均风速, Ci代表风向的发生概率。风能利用率也是评估风电场效率的关键指标,可以表示为:
\eta = \frac{{{P_{{\text{total}}}}}}{{{N_{\text{t}}}(0.3{u^3})}} (8) 成本估算模型认为投资成本与风电场中布置风力机总数有关,为了方便计算,无量纲化成本估算模型为单位1,其表达式为:
{f_{{\text{cost}}}} = {N_{\text{t}}}\left(\frac{2}{3} + \frac{1}{3}{{\text{e}}^{ - 0.00174{N_{\text{t}}}^2}}\right) (9) 因此,以单位输出功率的度电成本为目标函数
{f_{{\text{obj}}}} ,可以表示为:{f_{{\text{obj}}}} = \frac{{{f_{{\text{cost}}}}}}{{{P_{{\text{total}}}}}} (10) 3. 基于一阶网格法的风电场布局优化
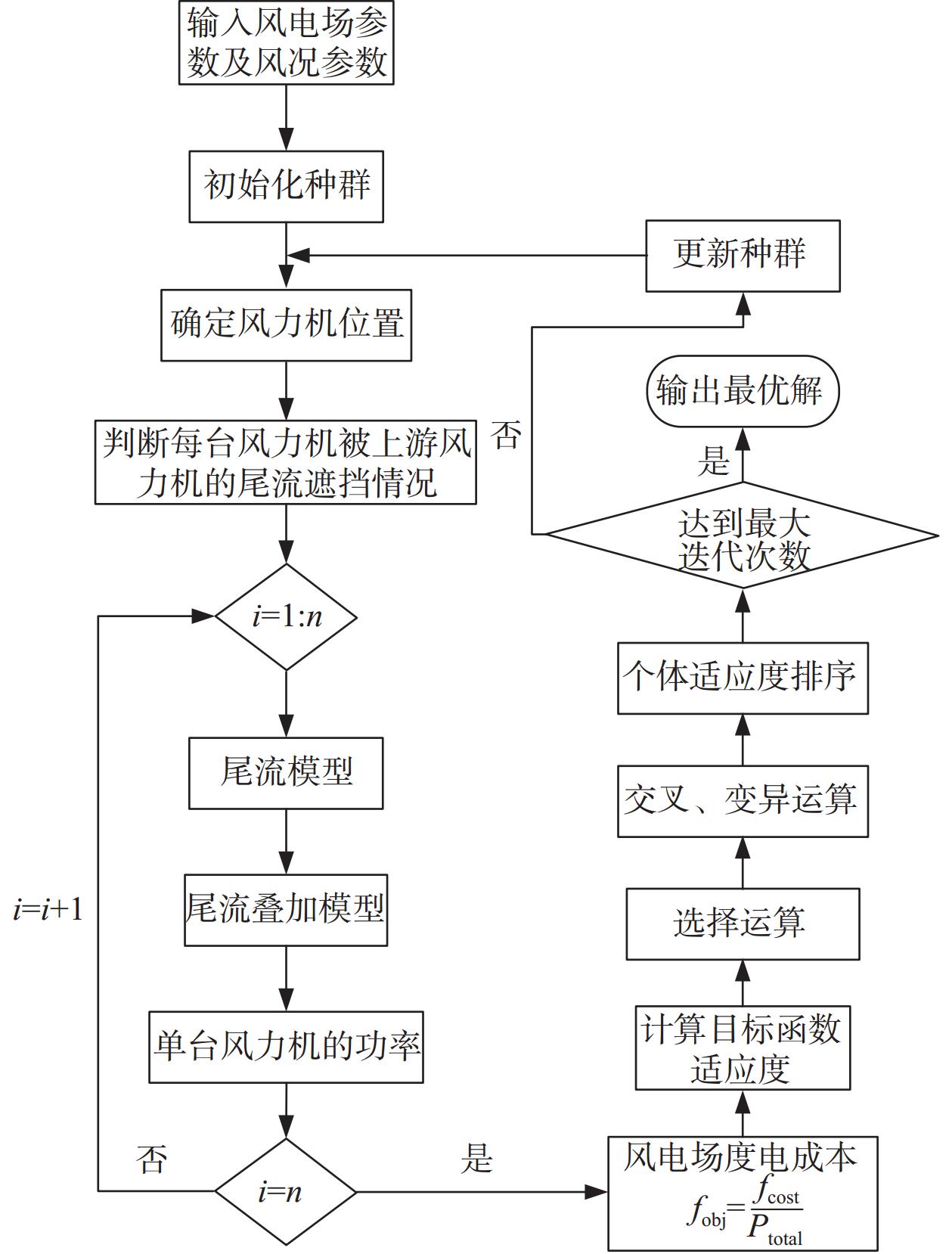
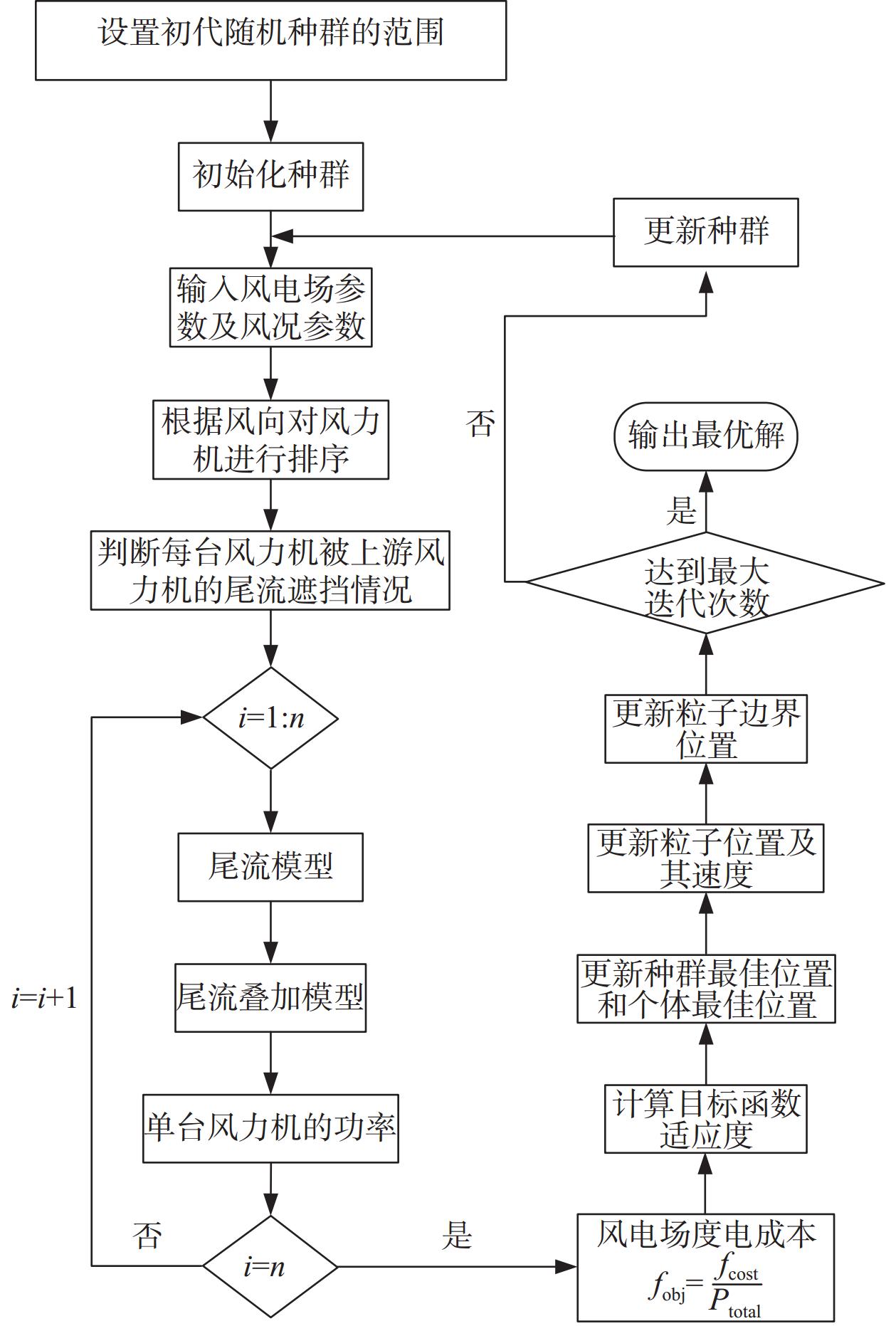
首先利用网格法对风电场布局进行第一阶优化。网格法将风电场离散为N × N的网格,假设风力机安装在网格中心,风电场有N2个安装点。用0代表网格中不存在风力机,用1代表网格中存在风力机,这将产生一个包含N2个元素的二进制字符串,然后采用遗传算法进行优化。图4为使用遗传算法优化风电场布局的流程图,其具体过程为:(1)输入风电场参数及风力机参数;(2)创建初始种群,种群中每个个体的维度为N2,每一个体表示一种可能的布局,种群中每个元素为[0,1]之间的随机数,并对每个元素进行取整运算;(3)确定风电场中风力机的个数及位置;(4)计算在对应风资源下风电场中的度电成本;(5)计算适应度值,并对种群中的个体进行交叉和变异运算;(6)将新的布局代入到第(4)步,直至收敛。
考虑到风电场的运行安全,风力机的间距通常设置为3D以上。将2 km×2 km的风电场划分为10×10的网格,任意相邻的两个网格中心的最小距离为200 m,其距离大于3D,所以任意相邻的两个网格中心都可以布置风力机。
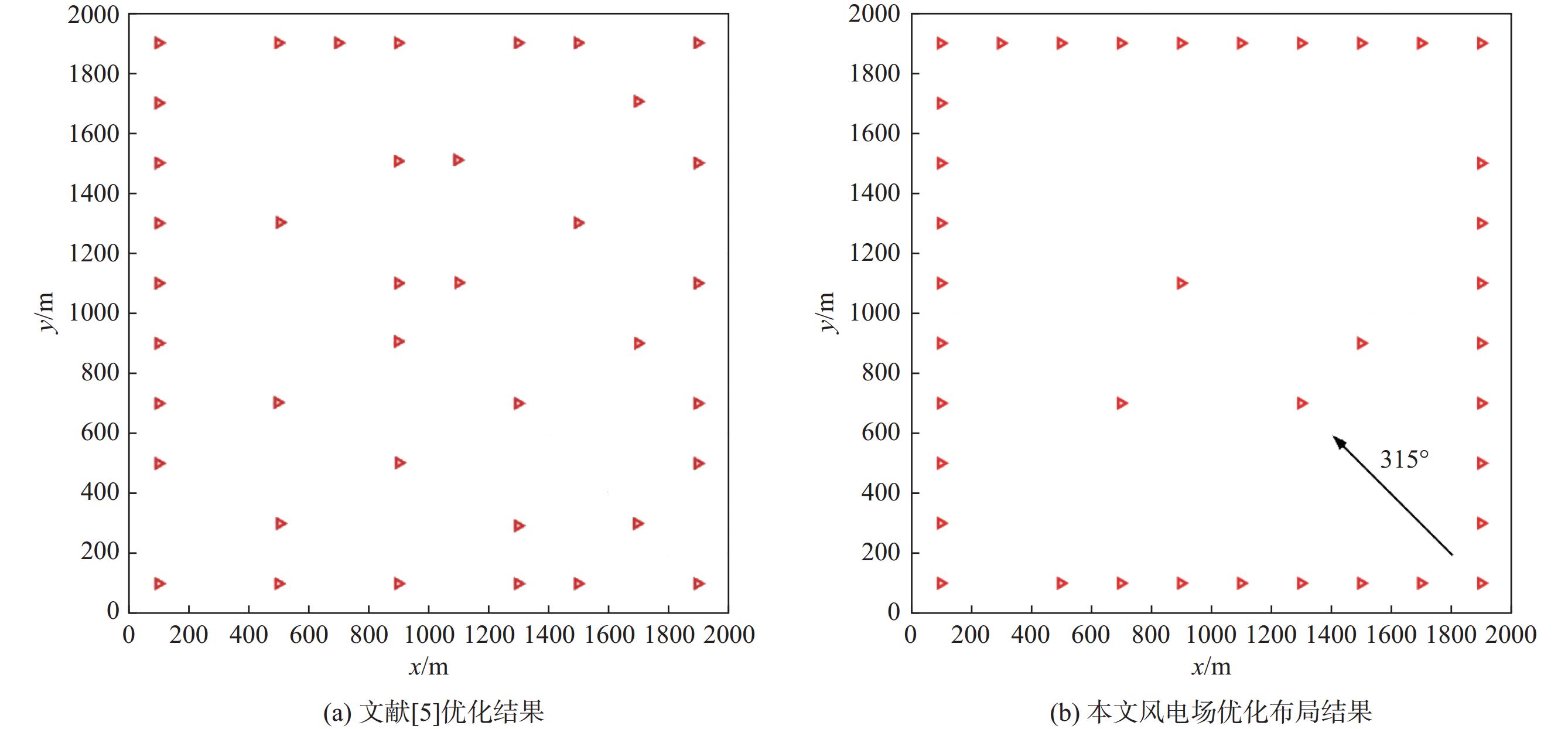
图5为一阶网格法风电场布局优化结果图,并与Grady等[5]二维结果进行了对比。由于风资源分布中主风向为280°到350°之间,在这个方向上风力机布置最密集,图5(b)中箭头表示风电场入流风向为315°。通过对比可知:本文基于三维尾流模型优化出的风电场布局主要沿着风电场的轮廓边缘布置,而中间布置的风力机只有4台;而二维尾流模型使得较多的风力机布置在中间,主要原因是其高估了尾流恢复速度(如图2所示)。因此本文采用的三维尾流模型的尾流分布特点与实验数据更加吻合,优化出的风电场布局更加合理。
表2为基于一阶网格法优化得到的风电场配置,与文献[5]的研究结果相比:风电场中风力机个数为38台,少1台;度电成本为0.878 2/W,略有增加。造成风电场中度电成本偏高及风电场效率偏低的原因是Grady等采用的是常规的二维尾流模型,在预测尾流速度分布时偏高,即二维Jensen尾流模型高估了尾流区域的速度恢复,导致风电场中下游风机能够获得较大的入流风速,使得总功率及风电场效率增加,度电成本降低。而本文采用的是考虑风切变效应的三维尾流模型,它能够合理评估风电场中尾流区域的速度恢复,使得计算的风电场总功率及效率较为合理。
表 2 不同尾流模型优化结果对比Table 2. Comparison of optimization results of different wake models变风速变风向 Ref.[5] 三维尾流模型 风力机个数 39 38 总功率/kW 32038 30373 度电成本/W–1 0.840 3 0.878 2 风电场效率/% 86.62 84.28 4. 基于约束区间的二阶布局优化
4.1 风电场二阶优化模型
网格法的优势是可推导出风电场中最佳的风力机安装个数,计算量较小,而缺点在于风力机安装在网格中心,限制了风力机布局的精确位置。坐标法[13]相较于网格法可以更加准确地确定风电场中风力机的最佳安装位置,但需要预先确定风电场中风力机的最佳安装台数。因此,本节采用坐标法对第一阶优化结果(已确定最佳台数)进行进一步优化。坐标法的优化策略为:假设风力机
i 在风电场中的安装点为(x_i ,y_i ),通过算法不断地在风电场区间中搜索风力机的最佳安装位置。由于不同的约束区间会对采用坐标法的优化布局结果产生影响,因此本文通过研究不同的约束区间对迭代速度与优化结果的影响确定风电场布局的准确位置,从而进一步提高风电场度电成本及总功率。
坐标法的第二阶优化过程中,约束条件如下:
\left\{ \begin{array}{l} 0 < {x_i} < X\\ 0 < {y_i} < Y \end{array}, \ \ \right.i = 1,2, \cdots ,{N_{\rm t}} (11) \left\{ {\begin{array}{*{20}{c}} {{x_i} - l_{\text{imit}} \leqslant {x_i} \leqslant {x_i} + l_{\text{imit}}} \\ {{y_i} - l_{\text{imit}} \leqslant {y_i} \leqslant {y_i} + l_{\text{imit}}} \end{array}},\ \ \right.{i = 1,2, \cdots ,{N_{\mathrm{t}}}} (12) 式(11)中X与Y分别代表风电场的长与宽,表示风力机被约束在风电场内。式(11)表示风力机
i 被限制在以当前坐标为基础预先确定的约束区间中,其中limit设置为5个不同的值,分别为50、100、150、200、250 m。x坐标的约束区间表示第i 台风力机限定在\left[ {{x_i} - l_{\text{imit}},\;{x_i} + l_{\text{imit}}} \right] 之间,y坐标的约束区间被限定在\left[ {{y_i} - l_{\text{imit}},\; {y_i} + l_{\text{imit}}} \right] 之间。\begin{split} &{{{\left( {{x_i} - {x_j}} \right)}^2} + {{\left( {{y_i} - {y_j}} \right)}^2} \geqslant 9{D^2}}\\ &\qquad {i = 1,2, \cdots ,{N_{\mathrm{t}}};\;j = 1,2, \cdots ,{N_{\mathrm{t}}}}; \; i \ne j \end{split} (13) 式(13)表示两台风力机之间最小的间距为3D。
图6为第二阶风电场布局优化算法的优化流程,和第一阶优化算法的主要区别为种群中个体的差别。在第一阶算法中,种群中的个体代表着网格中是否有风力机,第二阶算法中,种群的个体代表着风力机的坐标。种群个体的设定主要为:(1)提取网格法最优解中风力机的坐标,设置每台风力机的约束区间;(2)在每台风力机的约束区间内随机生成新的种群,种群中每个新个体中第[1, n]个元素为每台风力机的x坐标,第[n+1,2n]个元素为每台风力机的y坐标,且新个体必须满足约束条件,种群大小为个体维度的5倍;(3)以度电成本为目标函数,后续优化流程与网格法相同。
4.2 风电场二阶优化结果
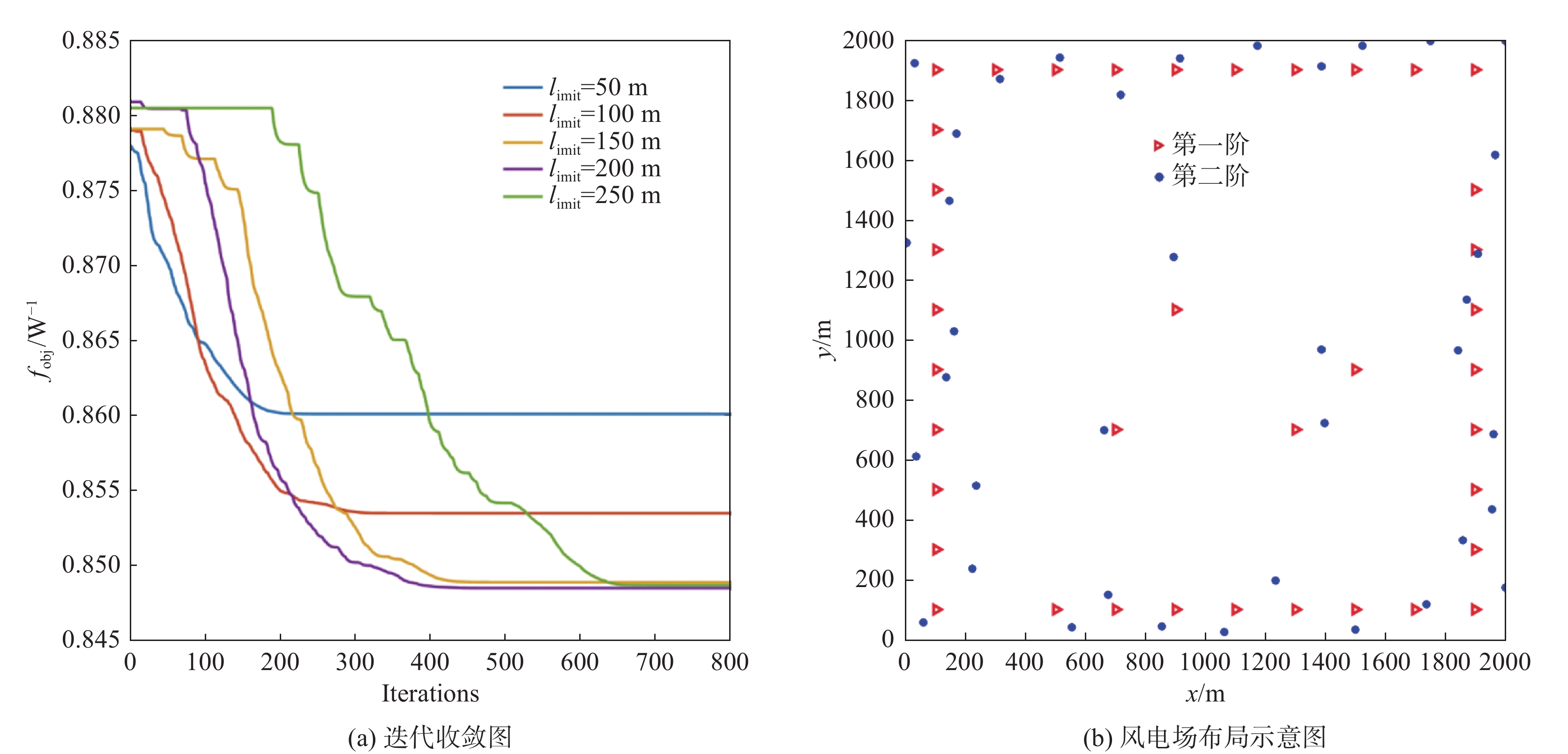
由于风速不恒定,风资源在280°~350°之间分布更加密集。第一阶算法优化后的风电场布局中,风力机主要沿着风电场的边缘布置。图7(a)为考虑不同约束条件下的第二阶风电场布局优化迭代图,图中纵坐标表示度电成本。由图可知:当约束条件限定为
l_{\text{imit}} = 50\;{\text{m}} 与l_{\text{imit}} = 100\;{\text{m}} 时,优化幅度较小;当约束条件限定为l_{\text{imit}} = 150\;{\text{m}} 与l_{\text{imit}} = 200\;{\text{m}} 时,迭代400次左右收敛,且优化幅度较大;当约束条件限定为l_{\text{imit}} = 250\;{\text{m}} 时,迭代650次左右收敛。图7(b)为约束区域
l_{\text{imit}} = 200\;{\text{m}} 时二阶风电场优化布局结果示意图。其中红色三角形为第一阶算法优化后的风力机位置,位于网格中心,蓝色点为第二阶算法优化后的风力机位置。相较于第一阶网格法优化结果,第二阶优化算法优化后风力机布置在网格中心的连线周围,这样可以更好地避免上游风力机尾流速度的影响。表3为不同约束区间二阶风电场布局优化结果对比。当第二阶算法约束区域限定为
l_{\text{imit}} = 50\;{\text{m}} 与l_{\text{imit}} = 100\;{\text{m}} 时,其度电成本在第一阶算法基础上分别降低了2.06%与2.81%,分别为0.860\;1 / {\mathrm{W}} 与0.853\;5 / {\mathrm{W}} 。当第二阶算法约束区域限定为l_{\text{imit}} = 150\;{\text{m}} 与l_{\text{imit}} = 200\;{\text{m}} 时,其度电成本均为0.848\;9/{\mathrm{W}} ,在第一阶优化算法的基础上降低了3.33%。当第二阶算法约束区域限定为l_{\text{imit}} = 250\;{\text{m}} 时,其度电成本最低为0.848\;7/{\mathrm{W}} ,在第一阶算法结果基础上降低了3.34%。表 3 不同约束区间二阶布局优化算法结果对比Table 3. Comparison of second-order layout optimization with different search intervals限制范围/m 度电成本/W–1 风电场效率/% 功率输出/kW ±0 0.878 2 84.28 30373 ±50 0.860 1 85.95 30999 ±100 0.853 5 86.61 31226 ±150 0.848 9 87.09 31384 ±200 0.848 9 87.09 31384 ±250 0.848 7 87.11 31387 综合考虑度电成本提升幅度和优化时间,当约束区域为
l_{\text{imit}} = 150\;{\text{m}} 与l_{\text{imit}} = 200\;{\text{m}} 时,第二阶优化算法计算效率较高,且目标函数优化结果理想,其度电成本较第一阶优化结果降低了3.33%。5. 结 论
本文基于改进的三维尾流模型和尾流叠加模型预测风电场中各风机的尾流速度,并通过实例验证了该三维尾流模型的准确性。采用网格法对风电场布局进行第一阶优化,在第一阶优化结果中,采用改进的三维尾流模型优化得到的风电场度电成本略高于Grady的研究结果,而总功率较Grady的结果略低。
第二阶风电场布局中采用坐标法确定合理的约束区间及微观布局。考虑5个不同的约束区间,并以第一阶风电场布局结果作为初始条件进行进一步优化,发现当约束区域为
l_{\text{imit}} = 150\;{\text{m}} 与l_{\text{imit}} = 200\;{\text{m}} 时,第二阶算法迭代速度较快,且其度电成本可进一步降低,相比第一阶风电场优化结果,降低了3.33%。 -
表 1 风电场及风力机参数
Table 1 Caculating parameters of wind turbine and wind farms
参数 值 风轮直径d/m 40 推力系数{C_T} 0.88 轮毂高度h/m 60 切入风速/(m·s–1) 2 切出风速/(m·s–1) 18 风电场的表面粗糙度{z_0}/m 0.3 表 2 不同尾流模型优化结果对比
Table 2 Comparison of optimization results of different wake models
变风速变风向 Ref.[5] 三维尾流模型 风力机个数 39 38 总功率/kW 32038 30373 度电成本/W–1 0.840 3 0.878 2 风电场效率/% 86.62 84.28 表 3 不同约束区间二阶布局优化算法结果对比
Table 3 Comparison of second-order layout optimization with different search intervals
限制范围/m 度电成本/W–1 风电场效率/% 功率输出/kW ±0 0.878 2 84.28 30373 ±50 0.860 1 85.95 30999 ±100 0.853 5 86.61 31226 ±150 0.848 9 87.09 31384 ±200 0.848 9 87.09 31384 ±250 0.848 7 87.11 31387 -
[1] JENSEN N O. A note on wind generator interaction [M]. Roskilde, Denmark: Risø National Laboratory, 1983.
[2] TAO S Y, XU Q S, FEIJÓO A, et al . Wind farm layout optimization with a three-dimensional Gaussian wake model[J]. Renewable Energy,2020 (159 ):553 −569 . doi: 10.1016/j.renene.2020.06.003[3] 宋翌蕾, 田琳琳, 赵宁 . 风力机三维尾流模型的提出与校核[J]. 太阳能学报,2021 ,42 (2 ):129 −135 .SONG Y L, TIAN L L, ZHAO N . Proposal and validation of a new 3D wake model for wind turbine[J]. Acta Energiae Solaris Sinica,2021 ,42 (2 ):129 −135 (in Chinese).[4] 汪泉, 柳柏杨, 胡聪, 等 . 改进风力机三维尾流模型及其风速预测准确性研究[J]. 可再生能源,2023 ,41 (6 ):773 −779 .WANG Q, LIU B Y, HU C, et al . Research on improved 3D wake model of wind turbine and accuracy of wind speed prediction[J]. Renewable Energy Resources,2023 ,41 (6 ):773 −779 (in Chinese).[5] GRADY S A, HUSSAINI M Y, ABDULLAH M M . Placement of wind turbines using genetic algorithms[J]. Renewable Energy,2005 ,30 (2 ):259 −270 . doi: 10.1016/j.renene.2004.05.007[6] LONG H, LI P K, GU W . A data-driven evolutionary algorithm for wind farm layout optimization[J]. Energy,2020 ,208 :118310 . doi: 10.1016/j.energy.2020.118310[7] LEI Z Y, GAO S C, WANG Y R, et al . An adaptive replacement strategy-incorporated particle swarm optimizer for wind farm layout optimization[J]. Energy Conversion and Management,2022 ,269 :116174 . doi: 10.1016/j.enconman.2022.116174[8] WANG L Y . Comparative study of wind turbine placement methods for flat wind farm layout optimization with irregular boundary[J]. Applied Sciences,2019 ,9 (4 ):639 . doi: 10.3390/app9040639[9] YANG P Y, NAJAFI H . A comparative study of multi-stage approaches for wind farm layout optimization[J]. Journal of Energy Resources Technology,2022 ,144 (10 ):101302 . doi: 10.1115/1.4053869[10] 蒋秋俊, 郑海涛, 杨庆山, 等 . 基于网格-坐标化遗传算法的风电场布局优化[J]. 太阳能学报,2022 ,43 (8 ):266 −272 .JIANG Q J, ZHENG H T, YANG Q S, et al . Wind farm layout optimization based on grid-coordinate genetic algorithm[J]. Acta Energiae Solaris Sinica,2022 ,43 (8 ):266 −272 (in Chinese).[11] 徐佳楠, 张天瑞, 李玉龙 . 基于自适应遗传-粒子群优化算法的风电场微观选址优化[J]. 科学技术与工程,2023 ,23 (16 ):6917 −6922 .XU J N, ZHANG T R, LI Y L . Micro-location and optimization of wind farm based on the adaptive GA-PSO algorithm[J]. Science Technology and Engineering,2023 ,23 (16 ):6917 −6922 (in Chinese).[12] 张子良, 郭乃志, 易侃, 等 . 几何约束条件下海上风电场布局优化方法研究[J]. 太阳能学报,2023 ,44 (2 ):116 −122 .ZHANG Z L, GUO N Z, YI K, et al . Investigation of offshore-wind-farm layout optimization under geometrical constraints[J]. Acta Energiae Solaris Sinica,2023 ,44 (2 ):116 −122 (in Chinese).[13] MORENO S R, PIEREZAN J, SANTOS COELHO L, et al . Multi-objective lightning search algorithm applied to wind farm layout optimization[J]. Energy,2021 ,216 :119214 . doi: 10.1016/j.energy.2020.119214[14] CHEN K X, LIN J, QIU Y W, et al . Joint optimization of wind farm layout considering optimal control[J]. Renewable Energy,2022 ,182 :787 −796 . doi: 10.1016/j.renene.2021.10.032[15] GUALTIERI G . Comparative analysis and improvement of grid-based wind farm layout optimization[J]. Energy Conversion and Management,2020 ,208 :112593 . doi: 10.1016/j.enconman.2020.112593[16] GAO X X, LI B B, WANG T Y, et al . Investigation and validation of 3D wake model for horizontal-axis wind turbines based on filed measurements[J]. Applied Energy,2020 ,260 :114272 . doi: 10.1016/j.apenergy.2019.114272[17] PORTÉ-AGEL F, WU Y T, CHEN C H . A numerical study of the effects of wind direction on turbine wakes and power losses in a large wind farm[J]. Energies,2013 ,6 (10 ):5297 −5313 . doi: 10.3390/en6105297 -
期刊类型引用(0)
其他类型引用(4)





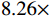

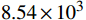

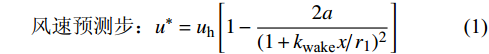
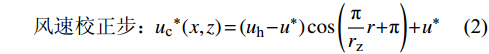
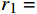
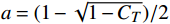
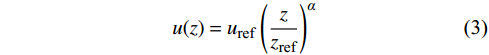
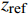
 下载:
下载: