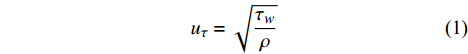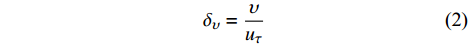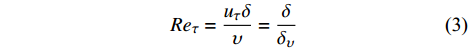Progress and outlook of plasma-based turbulent skin-friction drag reduction
-
摘要: 飞机摩擦阻力可占巡航总阻力的一半以上,减小飞机湍流条件下的摩擦阻力对于提升飞机巡航性能、降低燃油消耗具有重要意义。等离子体激励是等离子体在电磁场力作用下运动或气体放电产生的压力、温度、物性变化等对气流施加的一种可控扰动。采用等离子体激励减小飞机湍流摩擦阻力具有结构重量代价小、易于智能控制等诸多优势,受到国内外广泛关注。鉴于此,按照等离子体激励特性及其与湍流边界层的相互关系,将等离子体湍流减阻方法分为非定常激励、定常激励等类型,并梳理了其研究历程与进展。在平板湍流边界层中,等离子体激励能够诱导大尺度流向涡,产生输运作用,使摩擦阻力减小40%以上;在巡航迎角工况下的翼型上,激励同样能在20 m/s的来流速度下使翼型总阻力减小13.7%。发展新型高效能、高强度等离子体激励方法,实现高雷诺数、强逆压梯度气流环境下的湍流减阻,融入机器学习,推动开环控制向智能自适应发展,是等离子体湍流减阻技术未来的发展方向。Abstract: Aircraft friction drag accounts for more than half of the total cruising drag; thus, turbulent friction drag reduction is vital to improving flight performance and reducing flight costs. Plasma actuation is a controllable disturbance of pressure, temperature, and physical property changes caused by discharging gas or the moving plasma subjected to electromagnetic force. Compared to other turbulent friction drag reduction methods, plasma actuation has many advantages, such as lightweight and intelligent control capability, so it has received widespread attention. This paper provides a detailed overview of the development history and research progress of the plasma-based turbulent drag reduction method. In flat-plate turbulent boundary layers, plasma actuation can reduce friction drag by more than 40% by inducing large-scale vortical structures that enhance transportation. For airfoils at cruising angles of attack, plasma actuation can reduce the total drag of airfoils by up to 13.7% at a freestream velocity of 20 m/s. Developing new efficient plasma drag reduction actuation methods, adapting to flows with high Reynolds numbers and strong pressure gradients, and developing from open-loop blind control to intelligent adaptive control combining artificial intelligence, are the future development trends of the plasma-based turbulent drag reduction method.
-
0. 引 言
飞行阻力是飞机发展中面临的永恒问题。减小飞行阻力能显著增大飞机航程与航时,减小环境污染与燃油消耗,降低飞行成本。对于民用飞机,以波音747为例,在航程不变的前提下,每增加1%的阻力,则年燃油消耗量将增加约4.5×105 L[1-2]。对于军用大飞机和长航时无人机,飞行阻力也是影响其作战时间、任务载荷和作战半径的关键参数。在国际竞争逐步加剧,对我国军事能力要求不断提高,同时“碳中和”与“碳达峰”战略发展全面深化的大背景下,减小飞行阻力对于我国军用/民用飞机的发展都具有重要意义。
飞机飞行阻力从大的方面可分为两类:一类是由压强在来流方向上的投影造成的阻力,即广义的压差阻力;另一类是由飞机表面切应力造成的阻力,即摩擦阻力。如图1所示,以巡航状态的高亚声速大型运输机为例,上述两大类阻力约各占50%,其中广义的压差阻力又可继续分为由机翼气动力在来流方向上的分量造成的诱导阻力(约占30%)、由机翼表面边界层分离导致的机翼压差阻力(约占15%),以及后体阻力等其他阻力来源(约占5%)[2-3]。为减小飞机飞行阻力,研究者们针对不同的阻力构成发展了多种流动控制方法。
流动控制是指采用主动或被动的手段干预流场使其产生预期改变的方法[4-6]。针对机翼压差阻力,可通过涡流发生器[7]、机翼前缘吹/吸气[8]和等离子体激励[9]等方式抑制机翼表面边界层分离,从根源上减小压差阻力。针对诱导阻力和后体阻力等来源,则一般仅可采用气动外形优化或安装翼尖小翼等方法对其进行抑制[10-12]。在图1所示的各阻力来源中,摩擦阻力占比最大。除优化气动外形外(如层流机翼设计),采用流动控制的手段减小摩擦阻力的方法一般可分为两类:一是通过推迟边界层转捩,使飞机表面更大面积的边界层尽量处于摩擦阻力较小的层流状态以减小总摩擦阻力;二是在边界层转捩为湍流后,通过对湍流边界层内部结构的调控,减小湍流条件下的摩擦阻力[12-13]。
常用的推迟边界层转捩的方法有壁面抽吸和使用柔性复合材料蒙皮等[12],同时也有采用等离子体激励抑制圆锥边界层转捩的研究[14]。但在雷诺数较大的情况下,在飞机表面保持大面积的层流区难度较大,因此湍流边界层减阻成为流动控制领域的研究热点。自20世纪60年代 Kline等[15]发现湍流边界层中的近壁面相干结构以来,针对相干结构的调控,研究者们发展了复杂壁面[16-18]、边界层吹/吸[19-20]和展向壁面振荡[21-22]等多种湍流减阻方法,并取得了丰富的成果。基于介质阻挡放电(dielectric barrier discharge,DBD)的等离子体激励是一种新型的主动流动控制方法,具有结构简单、响应快、控制灵活等优点[23-24],有望以较小的结构与重量代价实现较好的减阻效果,成为一种理想的湍流边界层减阻手段。因此,DBD等离子体激励在湍流边界层减阻中的应用受到了国内外研究人员的广泛关注,同时也发展了多种DBD等离子体激励方式,并取得了良好的控制效果。
由于在等离子体湍流减阻技术发展过程中,对其他典型的湍流减阻方法多有借鉴,因此本文首先对除等离子体激励外的典型湍流边界层减阻方法进行简述;然后在此基础上详细论述国际上等离子体湍流减阻技术的研究进展,梳理发展脉络;最后对需要进一步深入研究的关键科学和技术问题,以及等离子体湍流减阻技术的发展趋势进行展望,以期为等离子体湍流减阻研究提供参考。
1. 典型湍流摩擦减阻方法
为寻求湍流边界层中随机流动行为的“稳定”规律,20世纪60年代以来,研究者们对湍流边界层中的流动结构进行了大量研究,结果表明,在边界层内部距离壁面的不同高度层中,存在不同的湍流相干结构与湍流行为,这些相干结构与湍流行为在湍流生成和摩擦阻力产生过程中作用显著[25-27]。采用流动控制手段对湍流相干结构进行调控,抑制湍流产生,是湍流摩擦减阻的重要思路。
在湍流边界层中,通常定义摩擦速度(uτ)和黏性长度尺度(δυ)作为边界层内层与黏性相关的速度尺度和长度尺度。二者的定义如下:
uτ=√τwρ (1) δυ=υuτ (2) 其中:τw为壁面切应力;ρ为空气密度;υ为空气的运动黏度。
基于上述黏性尺度定义的雷诺数称为摩擦雷诺数(Reτ):
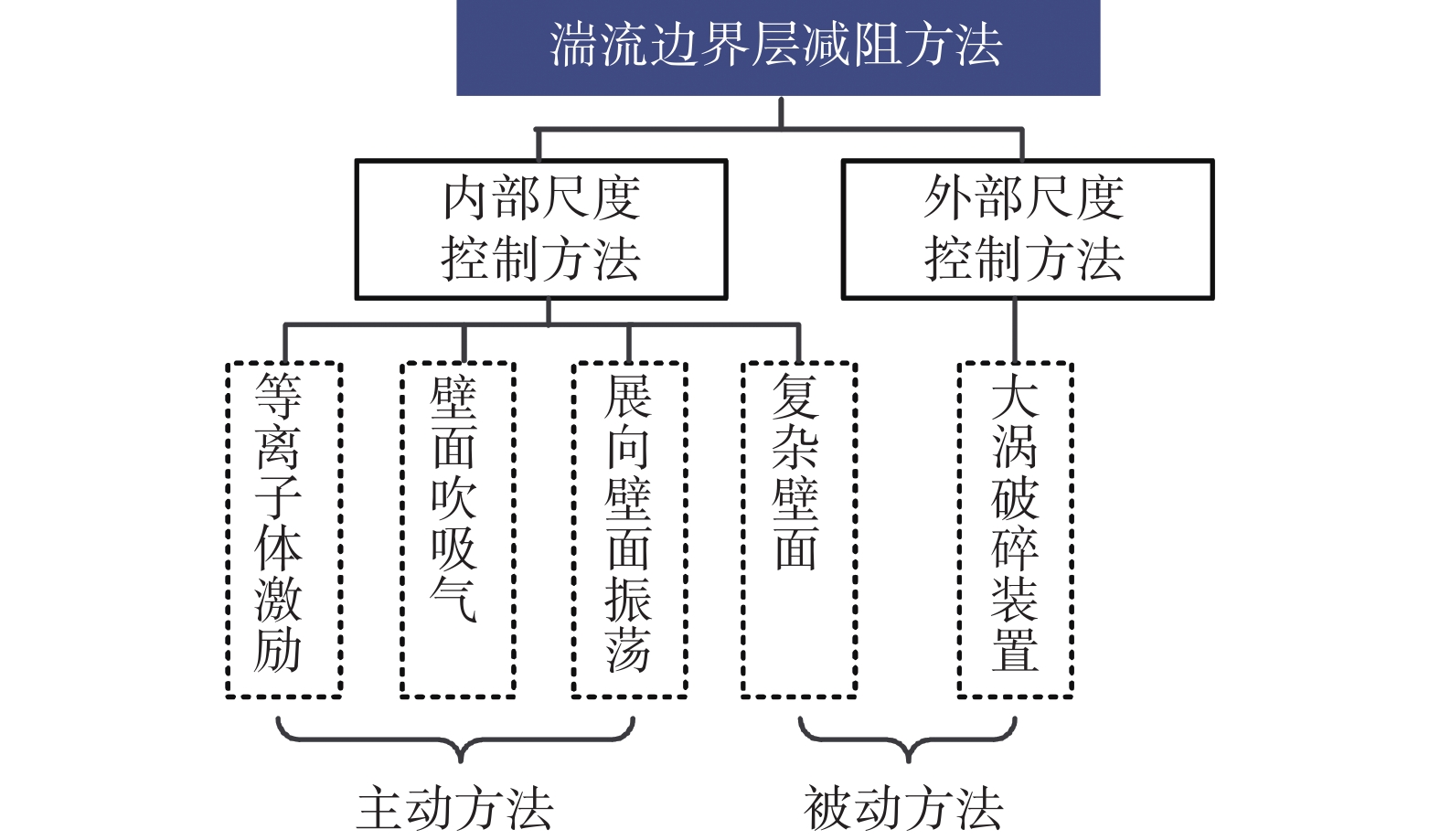
Reτ=uτδυ=δδυ (3) 其中,δ为边界层厚度。根据控制对象和控制机理的不同,一般可将湍流边界层减阻方法分为内部尺度控制方法和外部尺度控制方法两大类:内部尺度控制方法主要针对近壁面自维持过程或发卡涡结构对近壁面湍流行为进行控制;外部尺度控制方法主要通过控制边界层外区大尺度结构来对近壁面流动产生影响,进而影响壁面切应力[28]。内部尺度控制方法主要包括复杂壁面、壁面吹/吸和展向壁面振荡等;外部尺度控制方法则主要以大涡破碎装置为代表。典型主/被动湍流减阻方法的分类如图2所示。
1.1 复杂壁面
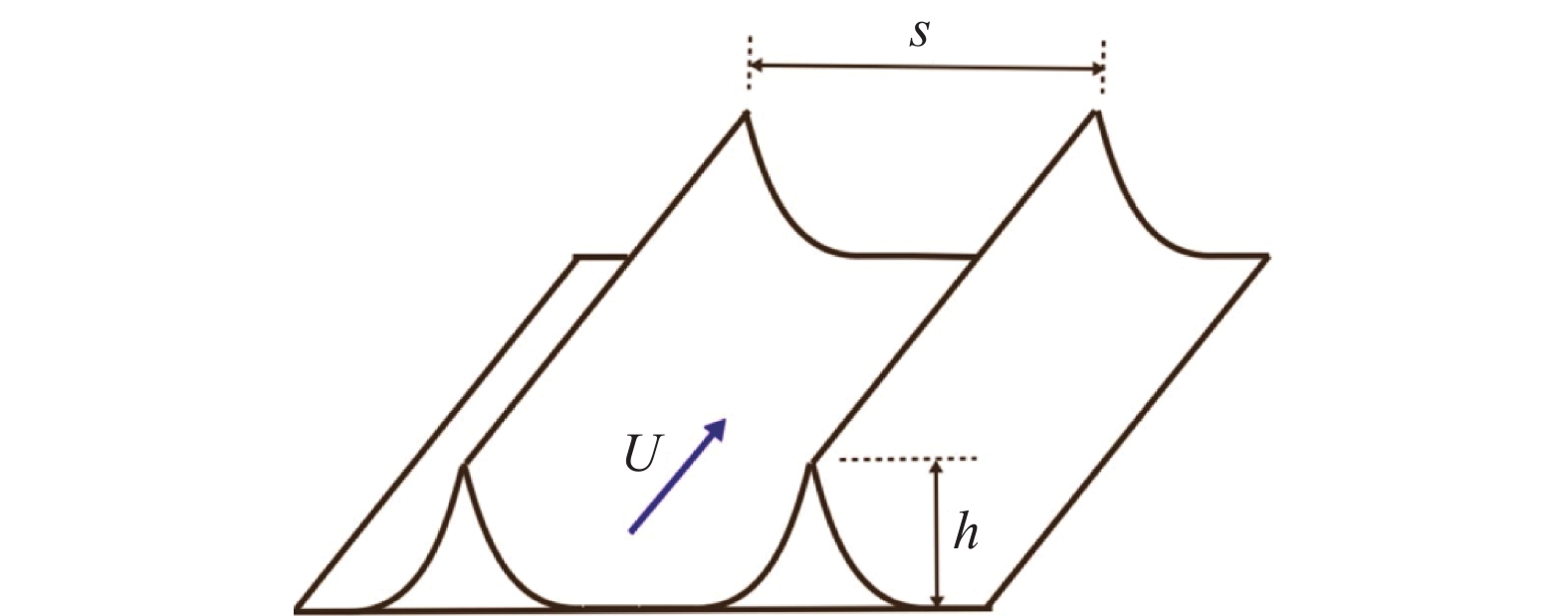
复杂壁面是指通过对壁面结构进行处理,影响近壁面湍流相干结构,从而实现减阻的被动流动控制方法,主要包括小肋(又名沟槽)、阵列凹坑、超疏水壁面和黏弹性的硅橡胶涂层等,其中小肋研究最为广泛[29]。小肋一般指壁面处沿展向周期性布置的流向突起或凹槽,如图3所示,其可通过抑制低速条带展向运动,减少猝发事件的发生,进而减小壁面摩擦阻力[30-32]。通常,当小肋高度为h = 8δυ~12δυ、相邻小肋展向间距s = 15δυ~20δυ时,减阻效果最好,能使摩擦阻力减小约8%~10%[16]。小肋等复杂壁面减阻方法的优点是无需能量消耗,缺点是当偏离设计状态时其减阻效果迅速减弱,这成为限制其应用的重要因素。
1.2 壁面吹/吸
壁面吹/吸是指,通过在壁面附近施加展向或法向射流以及采用边界层抽吸等方法控制边界层底层流动结构,进而实现减阻目的的方法。与复杂壁面等被动控制方法相比,壁面吹/吸属于主动流动控制方法,能够有针对性的设计控制策略对近壁面相干结构进行调控,实现更好的控制效果。基于吹/吸气以减弱边界层相干结构为目标进行反向反馈控制能够产生20%~30%的减阻效果[33-35]。此外,采用多孔介质表面进行法向均匀微吹气(如图4)能够实现50%~70%的局部相对减阻量[36-38]。壁面吹/吸方法减阻效果好、控制灵活,同时可实现多种复杂的控制策略,但也存在供气系统复杂、减阻代价高、多孔介质难以维护等问题。
1.3 展向壁面振荡
20世纪90年代,大量研究表明,瞬间变化的展向压力梯度能够有效降低边界层中的湍流生成和雷诺应力[39-42]。受此启发,研究者们开始采用非定常的展向壁面运动(如图5)进行减阻研究,自此展向壁面振荡减阻方法蓬勃发展。对于展向壁面振荡减阻方法,壁面振荡周期约为Tosc+=Tosc uτ2/υ ≈100[42]、振荡幅值Zosc+=Zosc uτ/υ ≈ 30时减阻效果最为显著[43],可实现40%左右的摩擦减阻量。展向振荡的壁面能够在湍流边界层黏性底层顶端诱导展向正涡量,展向正涡量与底层负涡量相抵消,减小底层法向速度梯度,进而减小摩擦阻力[44]。展向壁面振荡方法减阻效果好,但由于其机械结构复杂,且振荡过程中机械能损失较大,其减阻代价较大,难以实现减阻能量收益。
1.4 外部尺度控制方法
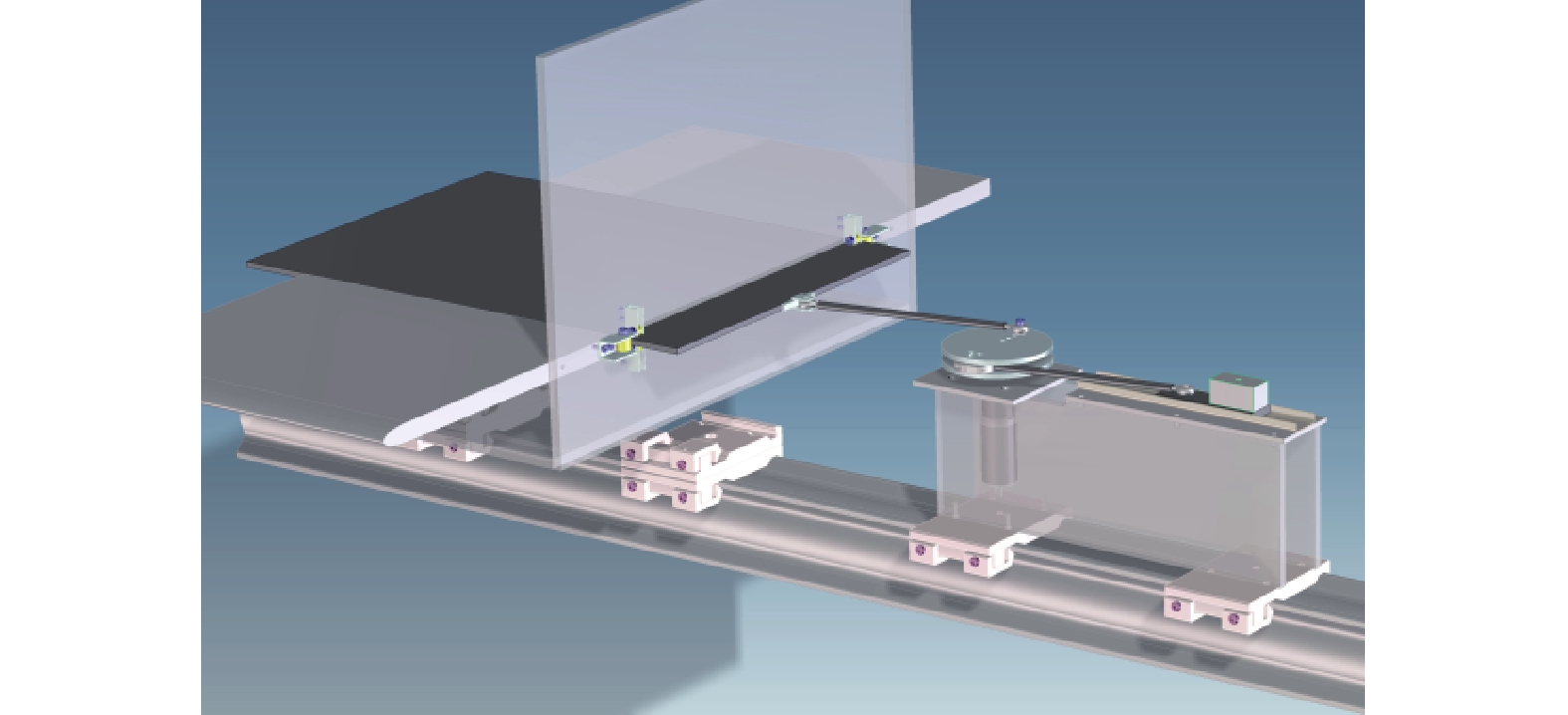
外部尺度控制方法主要以大涡破碎(large-eddy breakup, LEBU)装置为代表。LEBU装置一般由在湍流边界层一定高度处沿流向水平布置的薄平板构成,平板厚约0.002δ、长约0.8δ,布置高度在0.1δ~0.7δ之间,属于被动控制方法,旨在抑制边界层中的法向速度脉动,同时产生更多的小尺度结构,以实现减阻目的[46-48](如图6所示)。研究表明,采用LEBU装置能够有效抑制大尺度外区结构,使黏性底层厚度增加,猝发事件频率降低,进而使湍流摩擦阻力减小约20%[28]。LEBU装置无需能量输入,但其缺点在于在减小湍流摩擦阻力的同时,还会引入装置本身造成的型阻(属于压差阻力),同时该装置在实际边界层中的安装也较难实现。
2. 等离子体湍流摩擦减阻方法概述
采用等离子体激励进行流动控制的研究始于20世纪50年代,研究者们利用射频放电产生等离子体进行高速飞行器的激波减阻研究[49-50]。随后,采用介质阻挡放电(DBD)等离子体激励进行流动控制的研究逐渐兴起[51]。1998年,美国田纳西大学的Roth等[52-53]采用DBD对边界层进行了有效调控,引起了学界的广泛关注,自此,关于等离子体流动控制的研究大量涌现[23]。
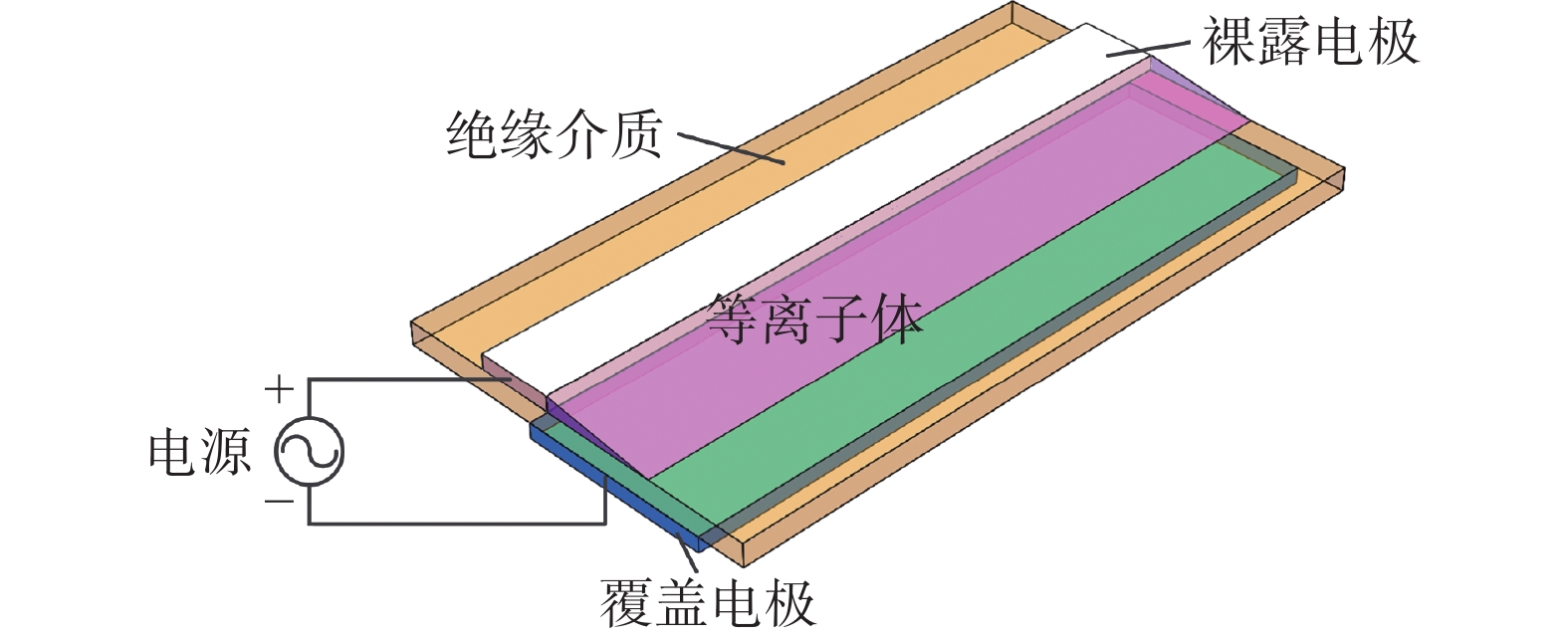
典型的DBD等离子体激励单元如图7所示,包括DBD激励器和高压电源两大部分。其中,DBD激励器由两条交错布置的条状电极以及将二者隔开的绝缘介质层组成,当高压电源产生的高电压施加到电极上时,介质层表面的空气便会电离形成等离子体[54]。
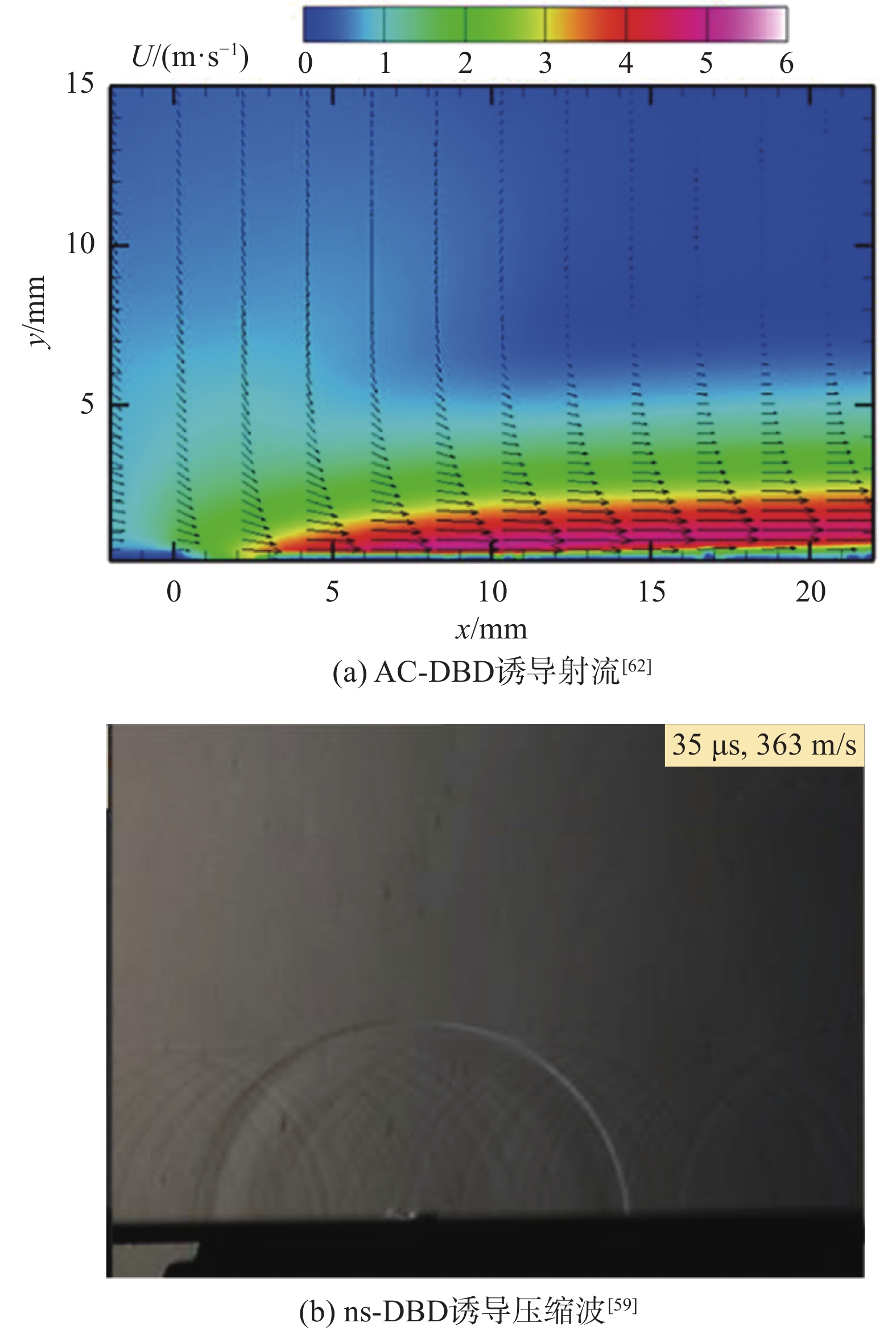
流动控制中,常用于驱动DBD的高压波形主要有两种:正弦波高压(AC-DBD)[23]和高压纳秒脉冲(ns-DBD)[55]。大量研究表明,AC-DBD主要通过持续的交变电场加速等离子体中的带电粒子,带电粒子与空气分子碰撞,从而在流场中产生射流和体积力作用[56-57]。AC-DBD诱导的射流结构,如ns-DBD,由于其脉宽较小,无法有效加速带电粒子,因此无法产生体积力[58-59],但由于其脉冲上升沿很陡,能够在上升沿处产生极强的电离,从而能够在200 ns左右的时间尺度内[60]产生60~160 K的局部温升[55],此加热时间尺度小于流场的声学时间尺度(≈300 ns)[61],因此能够在流场中诱导产生压缩波。AC-DBD诱导射流与ns-DBD诱导冲击波分别如图8(a,b)所示[59,62]。
此前,基于DBD的流动控制研究大多集中在翼型与机翼的大迎角流动分离控制方面。当把DBD激励器布置到机翼前缘时,AC-DBD的射流和体积力作用(或称动量效应)与ns-DBD的瞬时加热作用能够在机翼大迎角分离流场中诱导产生展向涡,使分离剪切层动态重附,或通过加速层流边界层转捩和促进内部流动掺混等途径抑制边界层分离,提高翼型大迎角状态下的升阻力性能[63-65]。研究表明,AC-DBD与ns-DBD诱导的动量效应与瞬时加热作用在翼型分离流场中的响应十分相似[66],但由于放电诱导速度的限制(<10 m/s)[67],AC-DBD仅能在Ma<0.4的情况下有效抑制流动分离[68],而ns-DBD在Ma = 0.74时仍有显著的流动控制效果[55]。目前,经多年发展,采用DBD进行大迎角分离控制的研究已能在小型无人机上成功应用,并进行了多次飞行验证,取得了良好的效果[69-70]。然而,该方法仅能通过抑制大迎角流动分离增大升力、减小机翼的压差阻力,在摩擦阻力主导的小迎角巡航状态下无法起到流动控制效果。由于客机、运输机、长航时无人机等多型飞机的绝大部分飞行时间均处于巡航状态,极少出现失速边缘的强分离、大迎角飞行,DBD等离子体流动控制技术的上述特点严重限制了其工程应用。近年来,由于飞行减阻的强烈需求和DBD的多种优势,采用DBD进行湍流摩擦减阻的研究重新成为新的研究热点。
基于等离子体放电的灵活性,研究者们在借鉴多种湍流边界层控制方法的基础上,基于DBD单元设计了不同的放电波形与电极结构,发展了多种等离子体湍流减阻方法,代表性的实验减阻效果如表1所示。综合分析,上述等离子体湍流减阻方法主要可分为非定常方法和定常方法等两大类,具体阐述如下。
表 1 不同等离子体湍流减阻方法的代表性实验减阻效果Table 1. Representative experimental results of different plasma-based turbulent drag reduction methods方法分类 高压波形 工作模式 研究对象 减阻效果 Reτ或Rec 来流速度/(m·s–1) 非定常方法 高压正弦波 展向振荡激励 零压梯度平板 >45% 475 1.75 [71] 展向行波激励 零压梯度平板 45% 475 1.75[71] 定常方法 高压正弦波 展向单侧激励 零压梯度平板 10% 572 2.4 [72] 展向对冲激励 零压梯度平板 26% 572 2.4[72] 展向对冲激励 翼型 - 2.07×106 170[73] 展向单侧激励 翼型 64% 4.97×104 5[74] 展向单侧激励 翼型 13.7% 1.99×105 20[74] 流向定常激励 零压梯度平板 65.1% - ≈ 4.5[52-53] 脉冲直流 展向单侧激励 零压梯度平板 - - 2.5[75] 展向单侧激励 零压梯度平板 >70% ≈ 2014 17.4[76] 展向单侧激励 零压梯度平板 ≈ 18% ≈ 4508 52.1[76] 展向单侧激励 逆压梯度平板 42% - 27.1[77] 展向对冲激励 零压梯度平板 ≈ 68% ≈ 4106 17.4[76] 展向对冲激励 零压梯度平板 ≈16% ≈ 6856 34.7[76] 3. 非定常等离子体减阻方法
非定常等离子体减阻方法主要包括展向振荡放电激励和展向行波放电激励两种。由于与来流相比,等离子体激励诱导的射流速度很小,因此绝大多数非定常等离子体减阻方法均沿展向(即垂直来流方向)产生射流,以期产生更强的扰动。
2000年,受展向壁面振荡湍流减阻方法的启发[78],美国麻省理工学院的Du等[79-80]通过直接数值模拟(direct numerical simulation, DNS)研究发现,在湍流边界层中施加“展向行波”能够有效抑制甚至完全消除近壁面条带结构,使湍流摩擦阻力减小50%以上,同时,在近壁面施加展向振荡的流动也能使条带和涡结构显著减弱,如图9所示。在数值模拟研究之外,他们还采用分布式的小电磁块,对展向行波和展向振荡流的减阻效果在盐溶液流动中进行了实验验证,实现了超消耗能量5倍的能量节省,该成果在Science期刊上发表[79],并被《流体力学年鉴》重点介绍[81],引起了广泛关注。Du等采用的“展向行波”和“展向振荡流”即为近壁面输运/振荡的体积力作用,这与AC-DBD的作用效果不谋而合。
3.1 展向振荡放电激励
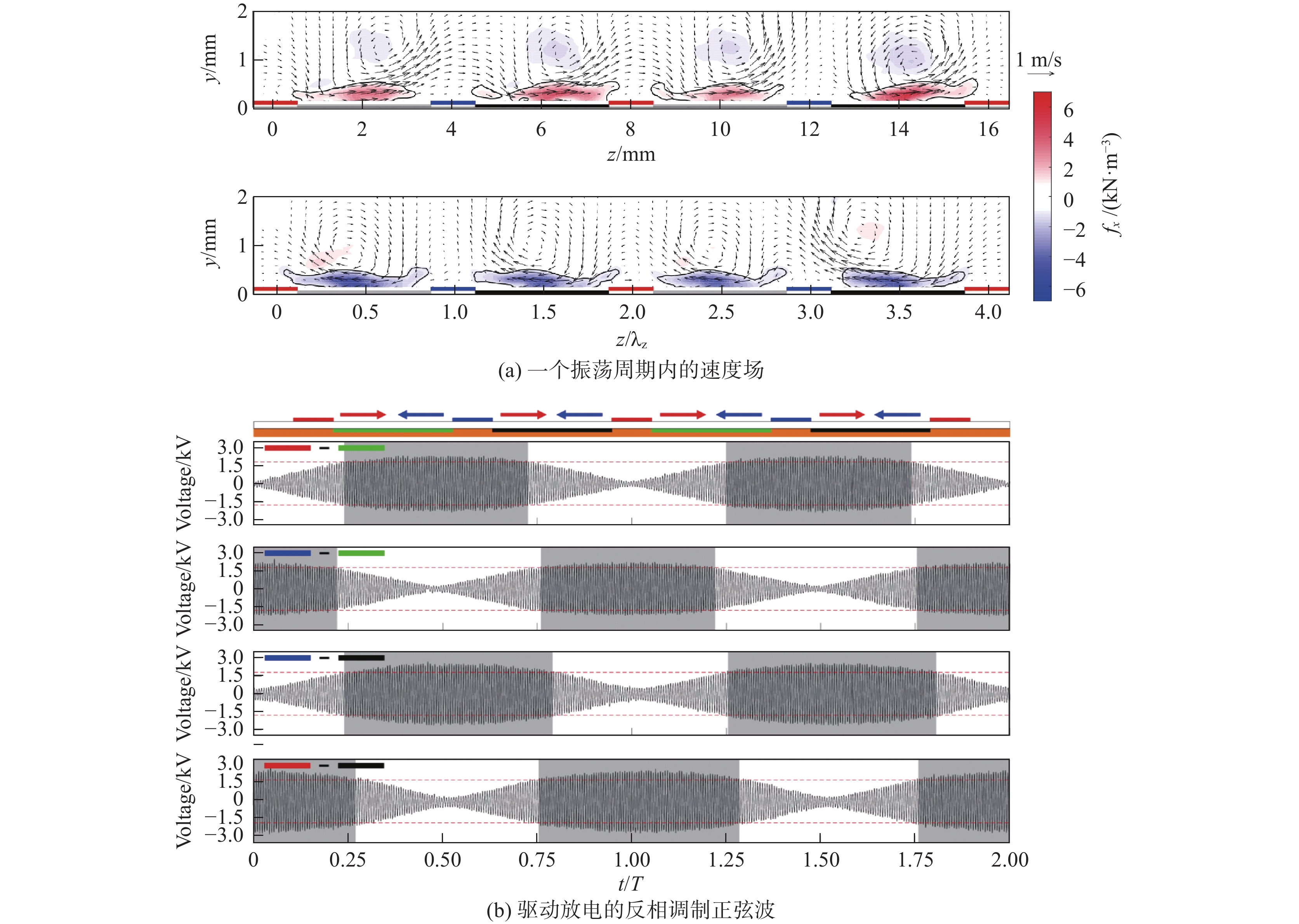
在Du等的研究之后,2003年,NASA兰利研究中心的Wilkinson[82]将两束正弦波高压叠加,形成一组占空调制的正弦波,然后在覆盖电极两侧各布置一条裸露电极,将两组反相的调制正弦波分别施加到两条裸露电极上,从而形成两侧交替放电的振荡DBD激励(如图10所示),产生振荡的体积力,模拟展向壁面振荡和展向振荡流的作用效果。在此基础上,采用热线探针与皮托管对不同振荡频率下的DBD诱导展向速度进行了测试,结果表明,随振荡频率的增大,放电诱导速度迅速衰减,放电诱导振荡仅能在低频情况下(<100 Hz)产生。因此,Wilkinson得出结论:由于有效振荡频率和强度的限制,DBD并不适合用于湍流减阻。随后,研究者们纷纷转向采用DBD控制流动分离的研究。此外,近期Hehner等[83-84]同样采用正弦波叠加的方法实现了振荡体积力,并对其特性进行了测试。
2006年,英国诺丁汉大学的Jukes和Choi等[85]在摩擦雷诺数Reτ = uτ δ/υ = 380(来流速度U∞ = 1.8 m/s)的条件下,通过热线探针测量平板湍流边界层速度剖面,然后根据湍流边界层对数律对速度剖面对数区进行拟合,进而对振荡DBD作用下的边界层湍流切应力进行了评估。结果发现,放电能够产生超过45%的相对减阻量,且减阻效果随振荡频率的增大而增强,显示出等离子体湍流减阻技术的巨大潜力。Jukes推测等离子体激励的减阻机理为:在边界层中诱导流向涡,与边界层底层准流向涡相互作用,破坏近壁面自维持过程,并且破坏边界层底层与外区间的联系,抑制发卡涡的生成,从而使边界层底层湍流强度减小,扫掠和猝发事件减弱,进而实现减阻。
对于展向振荡放电激励,除在时间域上产生振荡体积力外,在空间上进行振荡放电同样能有效减阻。英国华威大学的Elam[86]基于文献[87]的DBD模型,在Reτ = 200的条件下,采用DNS的方法对比了时间和空间振荡的放电在湍流边界层中的减阻效果。结果表明,时间振荡的减阻效果优于空间振荡,使湍流切应力减小41%,且随放电单元展向间距的增大,减阻效果逐渐减弱。近期,瑞典查尔姆斯理工大学的Altıntaş等[88]也采用DNS研究了流向空间振荡激励的减阻效果(如图11),在Reτ = 180和550的条件下分别减阻13%和11%,减阻效果随激励器展向间距的增大而减弱,与Elam的结论一致。
展向间距和振荡频率是影响振荡DBD减阻效果的关键参数。Jukes等[85]的研究表明,减阻效果随有效振荡频率的增大而不断增强,且激励器展向间距越小,减阻效果也越好。英国帝国理工学院的Mahfoze等[89]的DNS研究发现,Reτ = 475时,大展向间距的振荡放电使摩擦阻力增加75%,而仅打开一侧的放电则能使阻力减小33%;放电通过抑制高速流体的扫掠来抑制湍流的产生,进而减小摩擦阻力。近期,米兰理工大学的Alessio[90]进一步对不同展向间距的振荡放电进行了对比,并进一步强调了提高振荡放电强度与有效频率的必要性。
为提高振荡放电的有效频率,空军工程大学团队[91]采用锁相二维粒子图像测速(two-dimensional particle image velocimetry, 2D-PIV),对振荡DBD诱导流动的形成机理、演化规律和频率特性进行了研究与优化,并基于动量方程建立了振荡DBD诱导射流特性的解析模型。结果表明,随振荡频率的增加,射流发展时间和射流传播距离缩短,放电诱导流场由周期性振荡的展向射流转变为稳定在激励器中间的准定常法向射流,其展向射流速度与影响范围均迅速减小。在此基础上,对解析模型进行了验证,并提出了振荡DBD激励器的设计准则:在设计激励器时,应使射流传播距离尽量大,并满足射流传播距离大于低压电极宽度的一半。
3.2 展向行波放电激励
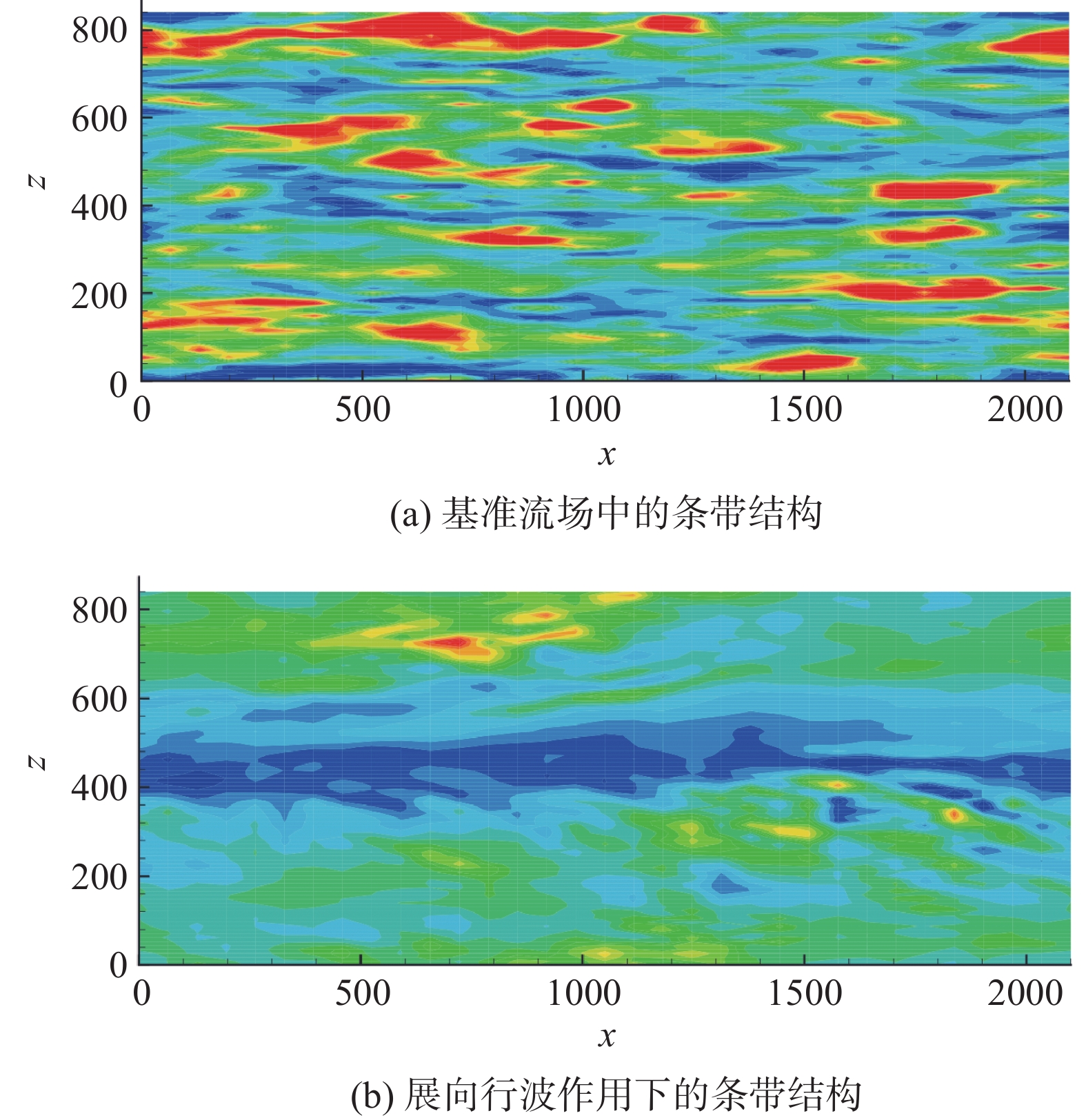
除展向振荡放电外,受Du等[79-80]的研究启发,Choi等 [71]采用多个正弦波电源依次驱动展向DBD阵列的各个单元,实现了如图12所示的展向输运体积力作用(即展向行波),并在与文献[85]相似的来流状态下(Reτ = 475、U∞=1.75 m/s),采用相同的流动测试方法对振荡和行波DBD阵列对湍流边界层及其壁面切应力的影响进行了研究。结果表明,行波DBD阵列也能产生与振荡DBD相似的减阻效果,使壁面切应力减小45%。Choi认为,放电诱导涡结构在展向行波放电减阻中起重要作用,但具体机理并不明确。
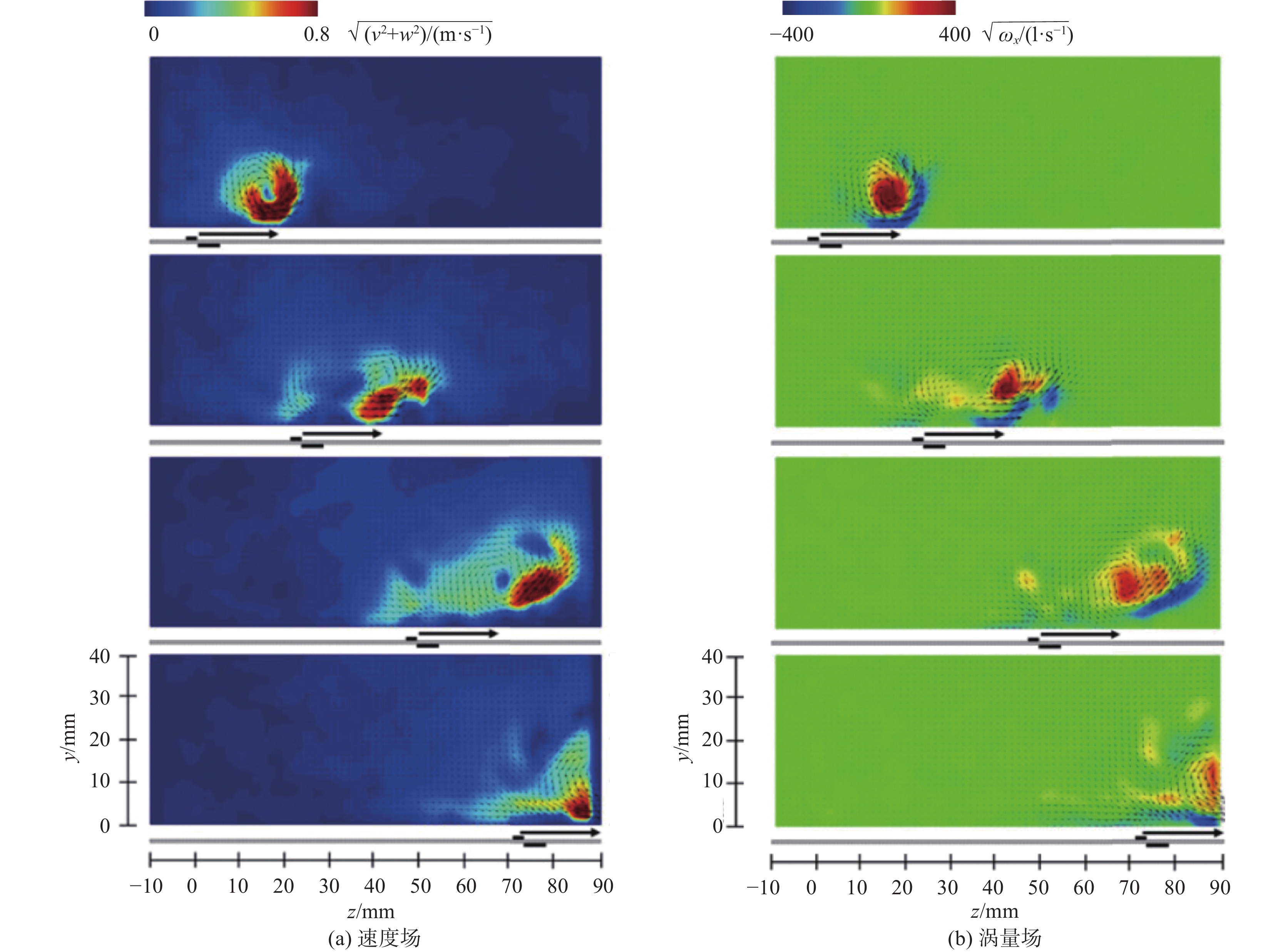
对于展向行波放电激励,Whalley等[92-93]采用PIV、热线风速仪等多种测试手段对放电诱导流动特性及其对湍流边界层的影响进行了系统研究。结果表明,在静止条件下,放电产生沿展向运动的单个启动涡,其运动距离可达100 mm;在平板湍流边界层中(Reτ = 435、U∞= 1.7 m/s),放电产生的展向输运的流向涡将黏性底层的低速流体沿展向铺展[94],同时使边界层原有的流向涡合并,导致近壁面低速流体在合并后的流向涡的诱导作用下抬升,并绕此流向涡运动[95],从而形成宽大的低速流体带,使近壁面低速条带消除。该实验结果与Du等[79]与Huang等[96]的DNS结果相似。在摩擦阻力层面,上述低速流体带处的壁面切应力与基准状态相比发生强烈的展向扭曲,与Zhao等[97]基于柔性壁面实现展向行波减阻的DNS结果一致。
目前,关于展向非定常式等离子体减阻方法的研究普遍能够产生超40%减阻效果,显示出等离子体湍流减阻方法的潜力。但是,由于等离子体激励强度本身的限制以及高频振荡下放电诱导展向速度的衰减作用,当前采用非定常式等离子体减阻方法的有效来流速度均仅为U∞ = 1~2 m/s;同时,在能量方面,放电消耗的能量超过其通过减阻所节省的能量的1×104倍[85],离实际应用尚有较大差距,因此还需对激励强度和减阻效果作进一步优化。
4. 定常等离子体减阻方法
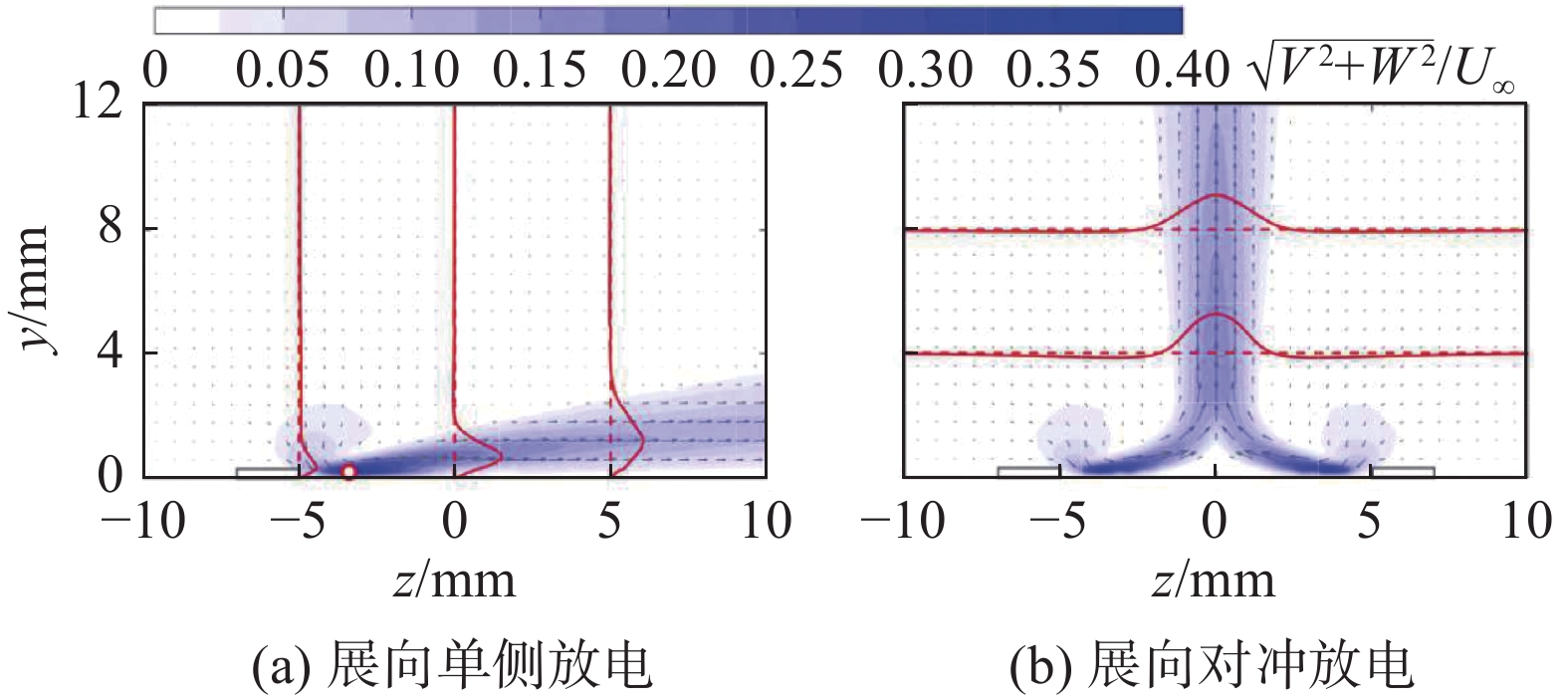
定常等离子体减阻方法是指不对放电波形进行调制,直接沿展向持续放电的减阻方法。与非定常方法相比,定常方法产生的时均扰动更强,将射流沿展向和流向布置均能有效减阻,因此其主要可分为展向定常减阻方法和流向定常减阻方法两大类,其中展向定常等离子体减阻方法可进一步分为展向单侧放电激励和展向对冲放电激励两种类型。展向单侧放电激励指仅在覆盖电极一侧放电产生等离子体,形成如图13(a)所示的单侧沿面射流,在边界层中产生类似展向吹气的作用效果;而展向对冲放电激励指在覆盖电极两侧同时产生等离子体,形成如图13(b)所示的对冲作用,在边界层中产生类似法向吹气的作用效果[26]。
非定常等离子体减阻方法主要基于高压波形的调制方式进行区分,但上述各类型的定常等离子体减阻方法的区别主要在于激励器的构型和布置形式。在驱动激励器工作的高压波形方面,采用高压正弦波(AC-DBD)或脉冲直流高压(pulsed-DC DBD)驱动相应激励器工作,均可实现上述不同类型的定常等离子体激励。为与上文保持一致,本节仍采用基于高压波形的分类进行阐述。
4.1 基于AC-DBD的展向定常放电激励
1998年,Roth等[52-53]进行DBD边界层调控时即采用了对冲式的展向定常等离子体激励方法,然而其结果表明,在雷诺数为1 × 105~1 × 106时展向对冲放电激励将使平板阻力增加。近年来,展向定常放电激励的减阻效果才逐渐显现。
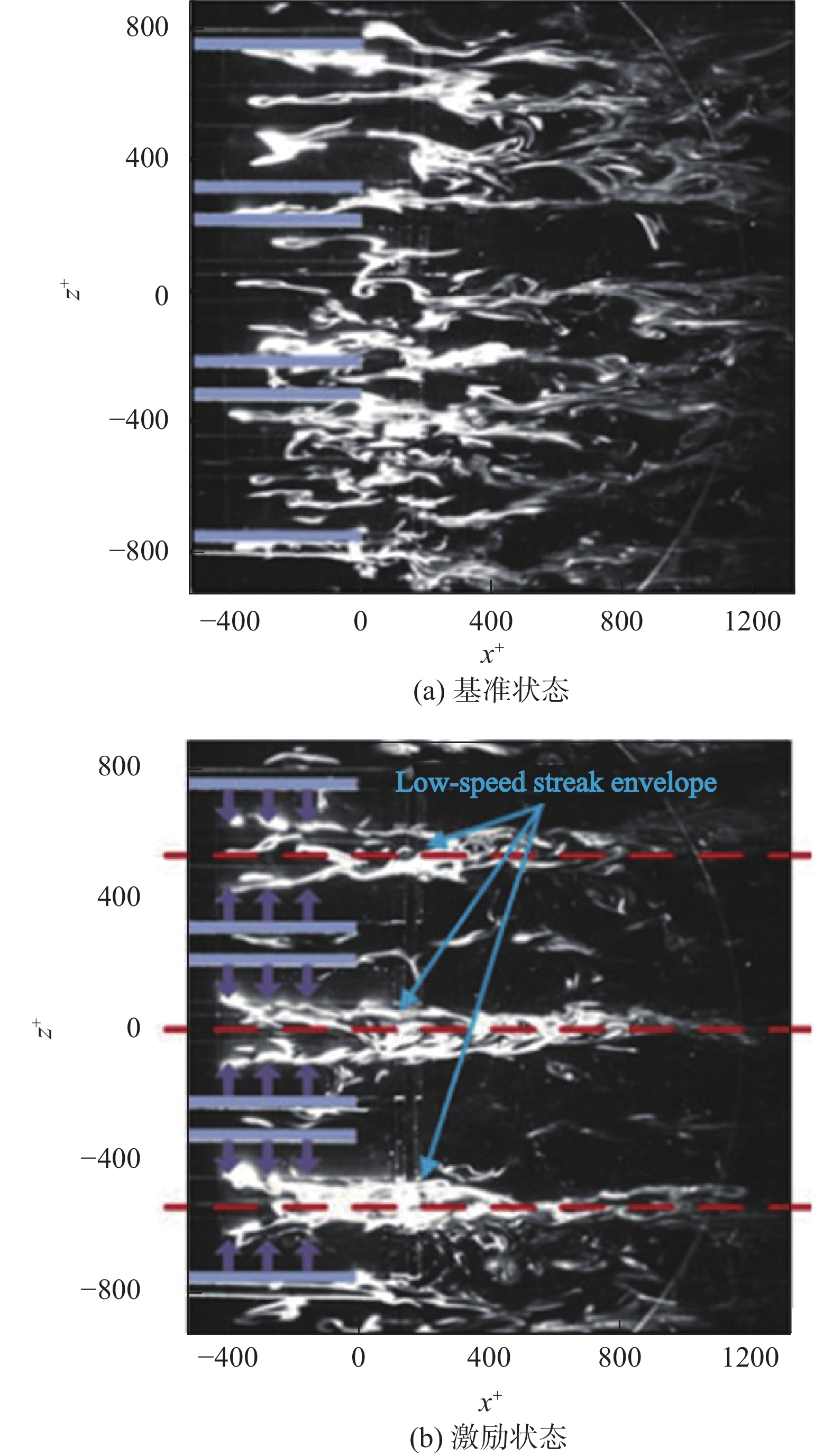
哈工大深圳研究生院的周裕教授团队[99]基于AC-DBD,采用测力、PIV、热线风速仪等多种测试手段,对不同间距的展向对冲放电激励和展向单侧放电激励在平板湍流边界层中的减阻效果开展了大量研究。结果表明,大间距的展向对冲放电激励减阻效果最好,且减阻效果随激励器流向长度的增大而增强,在U∞ = 2.4 m/s时能够减阻24%~26%[72,100-102]。放电在边界层中诱导方向相反的流向涡,稳定低速条带并使其向中间靠拢,形成狭长的低速条带群(如图14所示),在降低湍动能生成的同时减小流速,从而实现减阻的目的[72,101]。上述展向对冲放电聚拢条带结构的作用与Roth等的报道一致[52-53],但由于流场与放电条件的不同,减阻效果也不同。为进一步降低系统能量消耗,该团队对放电波形进行占空调制,并对减阻效果进行了测试。结果表明,占空调制放电激励将使低速条带不断聚拢分散,形成波浪式的条带分布,此时的减阻效果较定常放电激励弱,但由于占空比的影响,消耗功率更低[101]。近期,该团队还将前馈的比例微分控制系统引入到湍流减阻实验中,系统以最佳方案对激励器放电电压进行调节,在几乎不影响减阻效果的基础上使放电功率减小30%[103]。
西北工业大学的郑海波[104]采用热线测速的方法研究了放电频率对展向对冲放电激励的减阻效果的影响,结果表明,存在最佳放电频率200 Hz,在U∞ = 10.7 m/s时实现7.4%的局部相对减阻量。
为探究等离子体激励减小平板湍流摩擦阻力的作用机理,空军工程大学团队[75,98]基于高分辨的Stereo-PIV方法,对振荡放电、展向单侧放电、展向对冲放电三种激励方式在湍流边界层中诱导的流动结构、壁面切应力时空分布、湍流统计量、湍流猝发行为特征的变化进行了研究与对比。结果表明,三种激励方式均能在湍流边界层中诱导出比近壁面准流向涡尺度更大的流向涡,尽管该流向涡系的三维结构因激励方式而异,但均在湍流边界层中产生了明显的上扫和下洗作用,二者分别与减阻和增阻效果相对应,如图15所示。湍流边界层中的阻力变化主要是由激励诱导流向涡带来的动量输运造成,黏性项和湍流输运项的影响相对较小。在此基础上,建立了等离子体激励作用下的流向涡输运模型,模型计算与实验结果吻合良好,进而实现了对等离子体激励控制边界层及其摩擦阻力的作用效果的预测,为等离子体湍流减阻激励设计与效能评估提供了支撑。
4.2 基于脉冲直流DBD的展向定常放电激励
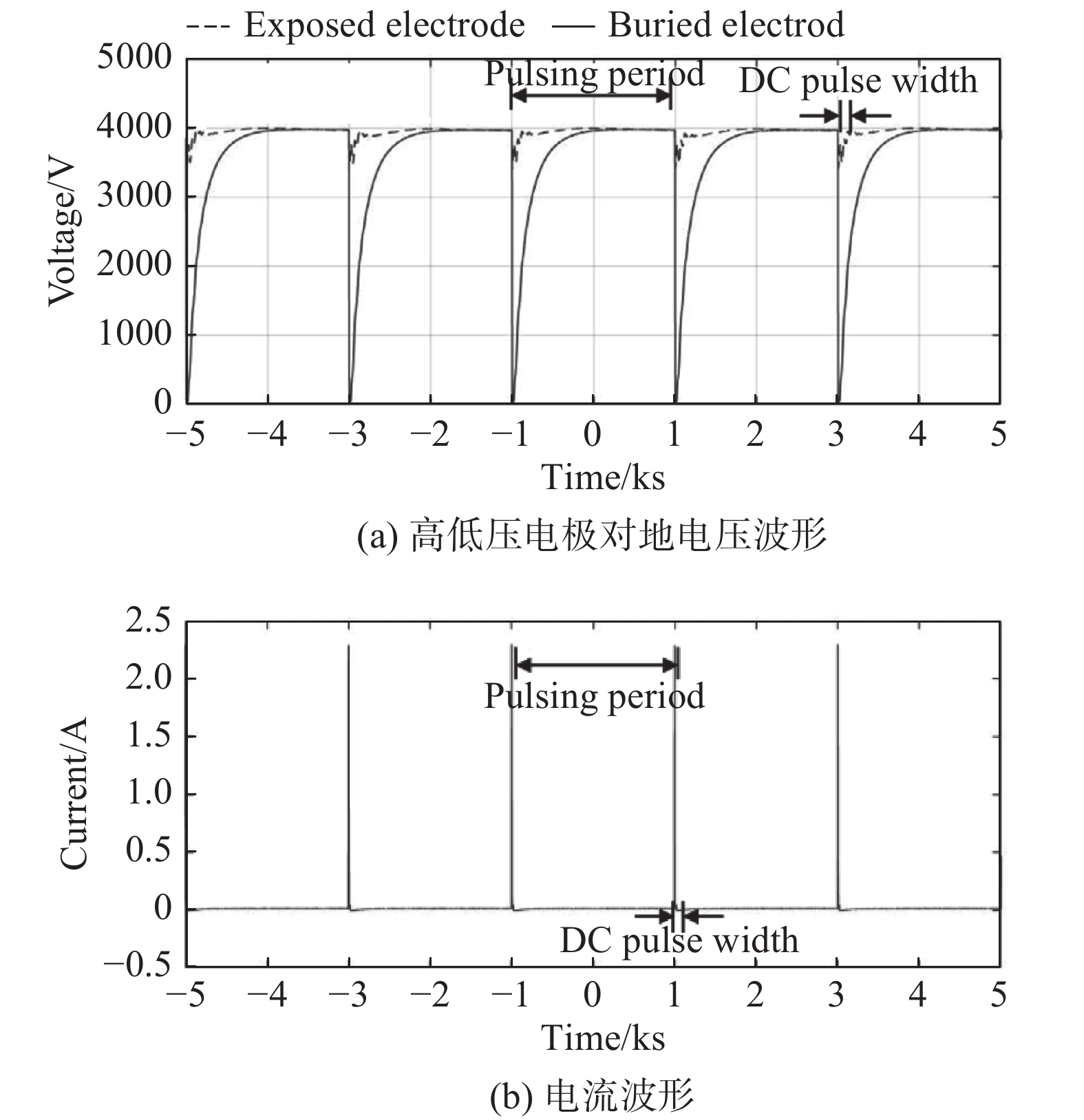
在展向定常等离子体减阻的研究中,除典型的AC-DBD外,还有一种新型放电波形,即脉冲直流(Pulsed-DC)放电波形。该波形于2016年由美国圣母大学的McGowan等[105]提出,并用于驱动DBD激励器。在放电电路中,将激励器裸露电极始终保持直流高压不变,低压电极在连接直流高压的基础上周期性接地,即可形成如图16所示的脉冲直流波形。McGowan等[105]的研究表明,使用该放电波形驱动DBD能够产生高达300 mN/m的体积力,比相似参数下的典型AC-DBD诱导体积力(约10 mN/m[56-57,67,106])高1个数量级。随后,McGowan等[105,107]将其应用到压气机叶片的流动分离控制中,并取得了良好的效果。
2019年,同一团队的Thomas等[76]将Pulsed-DC DBD应用到湍流减阻中,将激励器电极在平板湍流边界层中沿流向布置,采用高精度测量传感器(量程0.5N,精度0.08%),直接测量单侧定常和双侧对冲两种激励方式下的湍流摩擦阻力变化。结果表明,U∞ = 17.4 m/s时,激励使平板摩擦阻力减小70%以上,而当来流速度提高至U∞ = 52.1 m/s时,仍能产生约18%的减阻效果。放电电压越大,激励器单元展向间距越小,减阻效果越好。同时,由于所测得的Pulsed-DC DBD功耗极小(<1 W/m),放电通过减阻节省的功率可达所消耗功率的3倍以上,如图17所示。该项研究成果是惊人的,其将等离子体湍流减阻方法的有效来流速度提高了1个数量级,接近实际小型无人机的巡航速度,同时也实现了显著的净能量节省。
随后,该团队对脉冲直流放电特性及其湍流减阻机理进行了进一步研究。结果表明,在放电特性方面,Pulsed-DC DBD能够诱导产生12 m/s的瞬时速度,同时产生半圆形弱压缩波[76]。Sontag等[108]采用Shack-Hartmann 波前传感 (wavefront sensor WFS)方法对Pulsed-DC DBD在静止条件下的诱导速度进行了研究,发现放电诱导对流速度仅有0.96 m/s,同时其对边界层的影响并不显著,该结果与McGowan[105]与Thomas[76]等的实验并不相符。
在减阻机理方面,Duong等[109]的研究表明,放电使边界层速度脉动整体降低,通过基于热线测量的变量间隔时间平均(variable interval time averaging,VITA)的条件采样分析[110]发现,放电有效减小了上抛和猝发事件的频率,但对扫掠事件影响不大[109],而对热线数据的脉动速度象限分析表明放电同时减小边界层扫掠和上抛事件的频率[111]。Duong等[112]提出采用Pulsed-DC DBD减小湍流摩擦阻力的预期机理为:放电在边界层底层诱导展向射流,减小该处垂直于壁面的涡量分量,在条带瞬态增长(streak transient growth, STG)过程中抑制近壁面准流向涡的生成,进而破坏近壁面自维持过程,同时抑制条带结构的产生,减小湍流生成与壁面切应力。Cain等[113]通过改变边界层的湍流涡黏度,采用雷诺平均N-S方程(RANS)方法模拟了Pulsed-DC DBD使摩擦阻力减小后对民机和无人机模型飞行性能的影响,结果表明,放电能使民机燃油消耗减小12%以上,或使无人机作战半径翻倍。
上述基于Pulsed-DC DBD的研究取得了显著的控制效果,吸引了国际上的广泛关注,然而除美国圣母大学外,尚未有其他团队对该结果进行有效重复或验证。相反,日本东京农工大学的Nakai等[114]的研究表明,与圣母大学的结果不同,Pulsed-DC DBD产生的体积力仅为O(0.1 mN/m) 量级,诱导射流速度也小于1 m/s。在减阻效果方面,美国普林斯顿大学的Starikovskiy和莫斯科物理技术研究院的Aleksandrov等[115]在其综述文章中分析称,按文献[76]所示规律对曲线进行少量延伸即会得到负阻力(超100%的减阻效果,如图18所示),这显然是不符合物理规律的。Starikovskiy等[115]认为,上述问题可能是等离子体激励在平板表面诱导的流动分离干扰阻力测试而造成的,文献[76]的准确性及其结果产生的具体原因还需进一步验证与研究。
为验证Pulsed-DC DBD诱导体积力与减阻的能力,揭示作用机理,空军工程大学团队[116-117]从放电特性、诱导射流形态、体积力、冲击波和加热特性等多个角度对Pulsed-DC DBD进行了综合诊断与分析,并采用高分辨Stereo-PIV对Pulsed-DC DBD与湍流边界层的相互作用进行了分辨。结果表明,Pulsed-DC DBD的放电功率与典型的ns-DBD类似,处在O(10 W/m)量级,而其诱导体积力总体较同等参数下的AC-DBD低,处在O(1 mN/m)量级。Pulsed-DC DBD能在放电两侧同时诱导沿面射流,同时产生冲击波,但其最大射流速度仅在O(0.1 m/s)量级,该速度量级与Sontag等[108]的结果一致。Pulsed-DC DBD诱导冲击波、射流和体积力的机理为:在陡前沿处将空气快速电离产生等离子体,短时间内释放大量热量,并诱导产生冲击波;随后,等离子体中的带电粒子在电压缓慢下降阶段的高压维持电场中加速并与空气分子碰撞,产生动量效应。Pulsed-DC波形中的快前沿和大脉宽是其驱动DBD产生动量效应的主导因素,其高压直流的作用并不关键。上述拥有快前沿和大脉宽的高压波形称为“快升缓降”(fast-rise-slow-decay, FRSD)波形[117]。
在减阻效果与机理方面,Pulsed-DC DBD对湍流边界层的作用效果与AC-DBD基本相同,均是通过在边界层中所诱导的流向涡带来的动量输运改变壁面摩擦阻力,而黏性项和湍流输运项对阻力的影响相对较小[75, 98]。
4.3 流向定常等离子体减阻方法
流向定常等离子体减阻方法是指不对放电波形进行调制,直接沿流向持续放电的减阻方法,可分为逆气流放电激励、顺气流放电激励以及双侧放电激励等类型。除展向定常激励外,Roth等[52-53]同样采用了流向定常激励进行边界层调控。结果表明,逆气流激励使平板摩擦阻力增大,而顺气流激励使阻力减小,阻力减小量与激励阵列诱导的体积力之和相近,在来流速度约4.5 m/s时减阻65.1%,如图19所示,图中Erms=3 kV表示激励器上的电压的均方根为3 kV。上述减阻效果可理解为激励产生的推力对阻力的直接抵消。
2019年,西北工业大学的武斌等[118]将阵列式AC-DBD诱导射流沿流向布置于平板湍流边界层中,采用热线风速仪对流向定常放电下游的边界层速度剖面进行测试,并对速度剖面对数区进行拟合,计算壁面切应力,研究放电对平板摩擦阻力的影响。结果表明,与Roth等[52-53]的结果不同,逆气流与顺气流激励均能减阻,且逆气流放电的减阻效果比顺气流放电更好,U∞ = 14.1 m/s时使局部湍流切应力减小8.78%。激励能够使边界层底层速度减小,但更具体的减阻机理仍需进一步研究。
由于DBD诱导射流速度有限[67],同时边界层中流向速度远大于展向速度,因此,与展向放电方法相比,流向定常等离子体减阻方法也存在控制效果随来流速度的增大而迅速衰减的问题。
5. 翼型等离子体湍流减阻的探索
除在平板上的零压力梯度的湍流边界层(zero pressure gradient turbulent boundary layer, ZPGTBL)中进行研究外,为将等离子体湍流减阻技术推向应用,研究者们还进行了压力梯度条件下的湍流减阻以及巡航迎角状态下的翼型减阻研究。
在有逆压梯度(adverse pressure gradient, APG)的平板湍流边界层中,美国圣母大学的Yates等[77]采用对数区速度拟合的方法计算阻力,研究了Pulsed-DC DBD的减阻效果。结果表明,逆压梯度为223 Pa/m、U∞ = 27.1 m/s时,减阻效果仍可达42%。西北工业大学的李跃强等[73]采用MEMS热膜方法测试了Ma = 0.3~0.5范围内、贴附在NACA0012翼型表面的双侧对冲式AC-DBD激励器下游的摩擦阻力(如图20),这是等离子体湍流减阻方法在翼型上的首次尝试,但遗憾的是并未取得减阻效果。
空军工程大学团队[74-75]将展向阵列DBD应用到0°与6°迎角下的NACA0012翼型上,基于尾迹测量,对单侧定常放电、双侧对冲放电、振荡放电作用下的翼型总阻力的变化规律进行了研究,并初步探讨了翼型减阻机理。结果表明,当来流速度为U∞ = 5 m/s和20 m/s时,单侧定常放电激励可分别使翼型总阻力减小64%和13.7%;双侧对冲放电激励使阻力略有增加;振荡放电激励则介于二者之间,且随振荡频率的增大,减阻效果减弱。
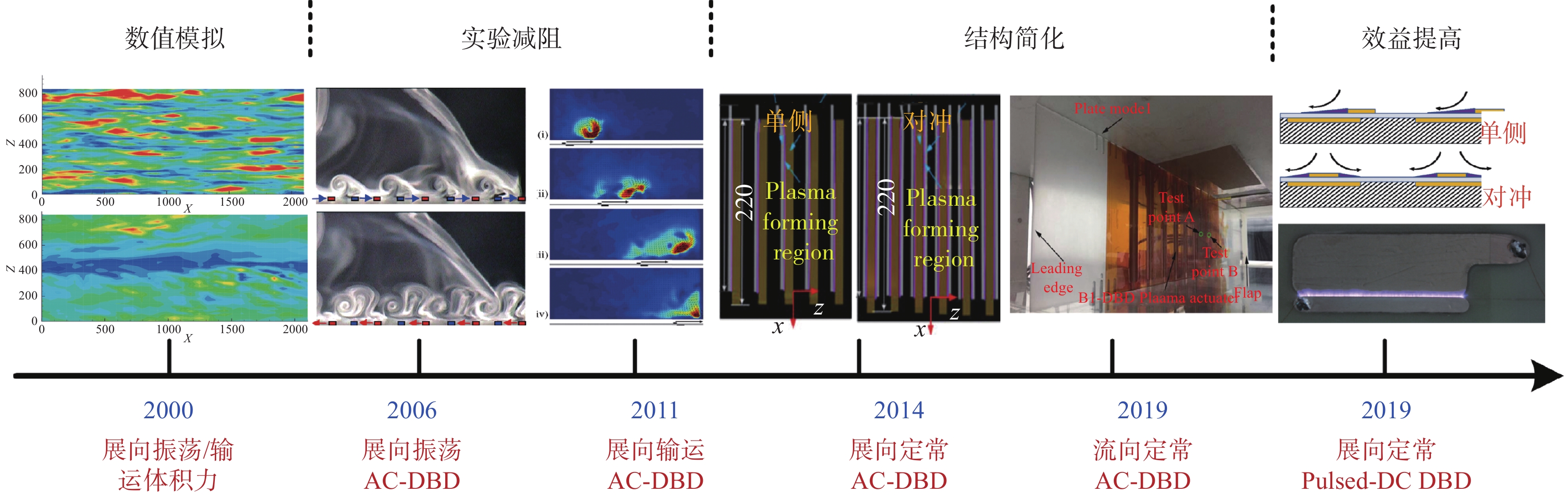
进一步,基于射流速度(v)、来流速度(U∞)和展向电极组间距(L)等参数,构建了反映空间尺度影响的无量纲电极组间距(L+ = L/δυ)和反映激励强度影响的射流速度比(r = v/U∞)等无量纲参数,并提炼了影响翼型减阻量的无量纲相图(如图21所示)。结果表明:r较小时(r < 0.05),激励强度过弱,无法对阻力产生影响;r > 0.05时,在对数坐标系下,阻力变化量随r和L+线性增加;r = 0.05属于状态的边界,可归于影响较小的区间。基于上述参数影响规律,对减阻量构成、湍流减阻机理和减阻效率进行了分析,相关结论可为翼型等离子体湍流减阻系统的优化设计提供理论支撑。等离子体湍流减阻技术的发展历程可初步总结为图22。
6. 展 望
本节从激励方法、应用环境与控制策略三个方面对等离子体湍流减阻技术的发展进行展望。
6.1 激励方法:发展新型高效能等离子体减阻激励方法
湍流减阻的目的在于节约能耗,进而增大飞机的航程和航时、减少燃油燃烧带来的环境污染和碳排放。因此,对于等离子体激励等主动湍流减阻方法而言,以更小的能耗产生更强的减阻效果(即更高的效能)是其永恒的发展目标。
激励方法是减阻效果产生的根源。在现有的主动湍流减阻方法中,虽然等离子体湍流减阻装置的结构重量大大简化,但是由于其有效减阻来流速度低,目前基于AC-DBD的等离子体湍流减阻方法所能实现的能量收益极其有限;而脉冲直流激励虽然减阻能量节省效果显著,但其效果尚未得到验证。因此,发展新型高效能等离子体减阻激励方法成为提高等离子体湍流减阻效能的根本途径,也是当前等离子体湍流减阻技术发展的首要需求。
解决上述问题主要有以下两个方向:一是基于现有减阻机理,提高等离子体激励的产生效益;二是创新减阻机理,发展新型等离子体激励方式。
首先,在提高等离子体激励本身的产生效益方面,综合上文分析可见,各类等离子体湍流减阻方法均是通过在流场中产生各种形式(流向、展向;定常、非定常)的动量效应(射流与体积力作用)以实现减阻效果。因此,基于现有减阻机理,通过优化等离子体激励驱动波形、改进等离子体激励器结构等方法提高激励本身产生动量效应的效能是提高减阻效能最直接的方法。例如,文献[105,117]中针对脉冲直流、快升缓降等波形的研究即是在波形优化方面的尝试,文献[91]对振荡放电高频工作特性的优化则是面向激励系统的整体提升。除上述方法外,还可通过减小激励器裸露电极宽度从而增强放电区域电场,来提高体积力产生效益;或通过增大激励器组密度等方法,提高单位面积内的放电长度,增大单位减阻面积内的体积力强度,从而实现更强的减阻效果。
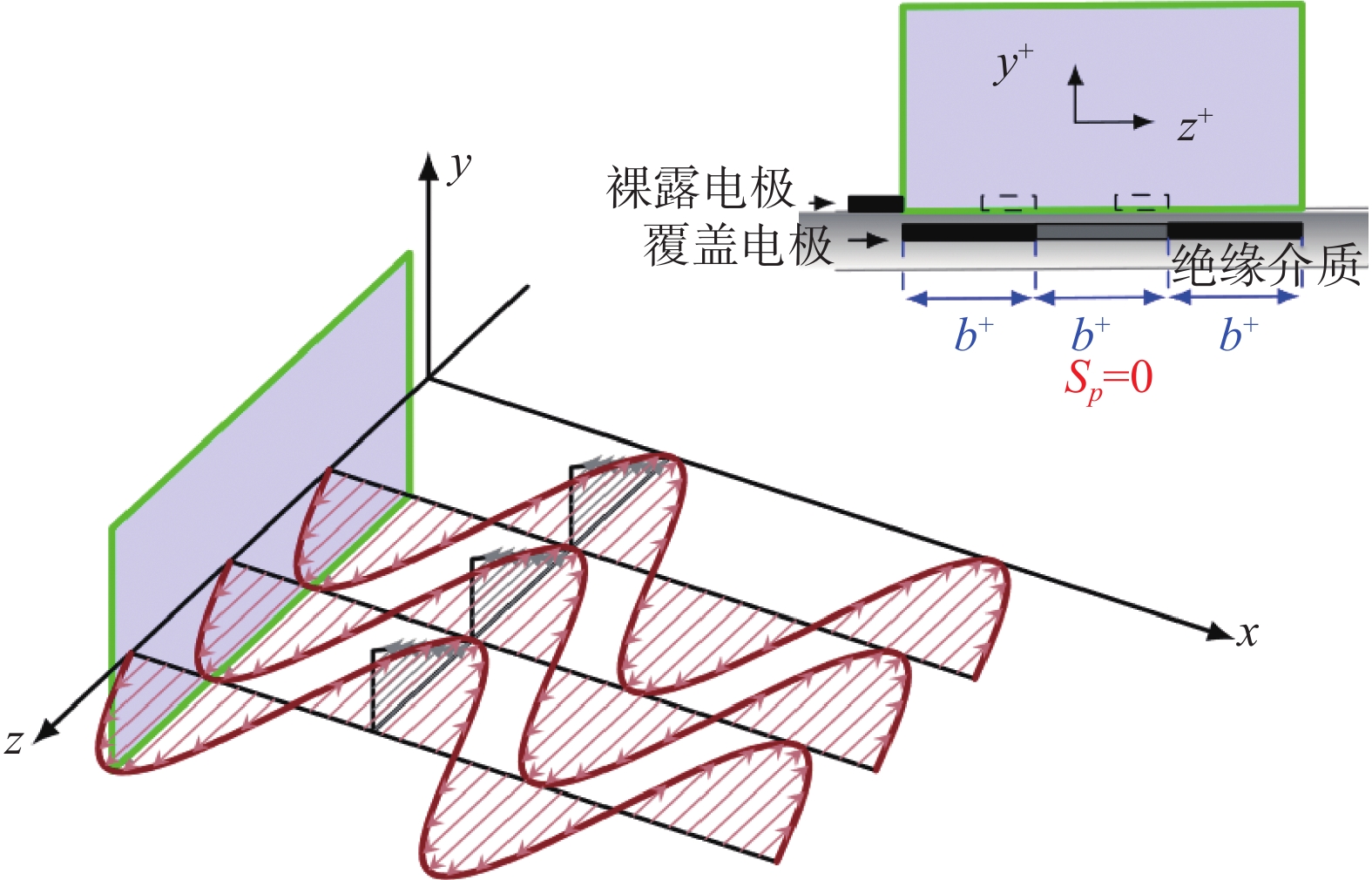
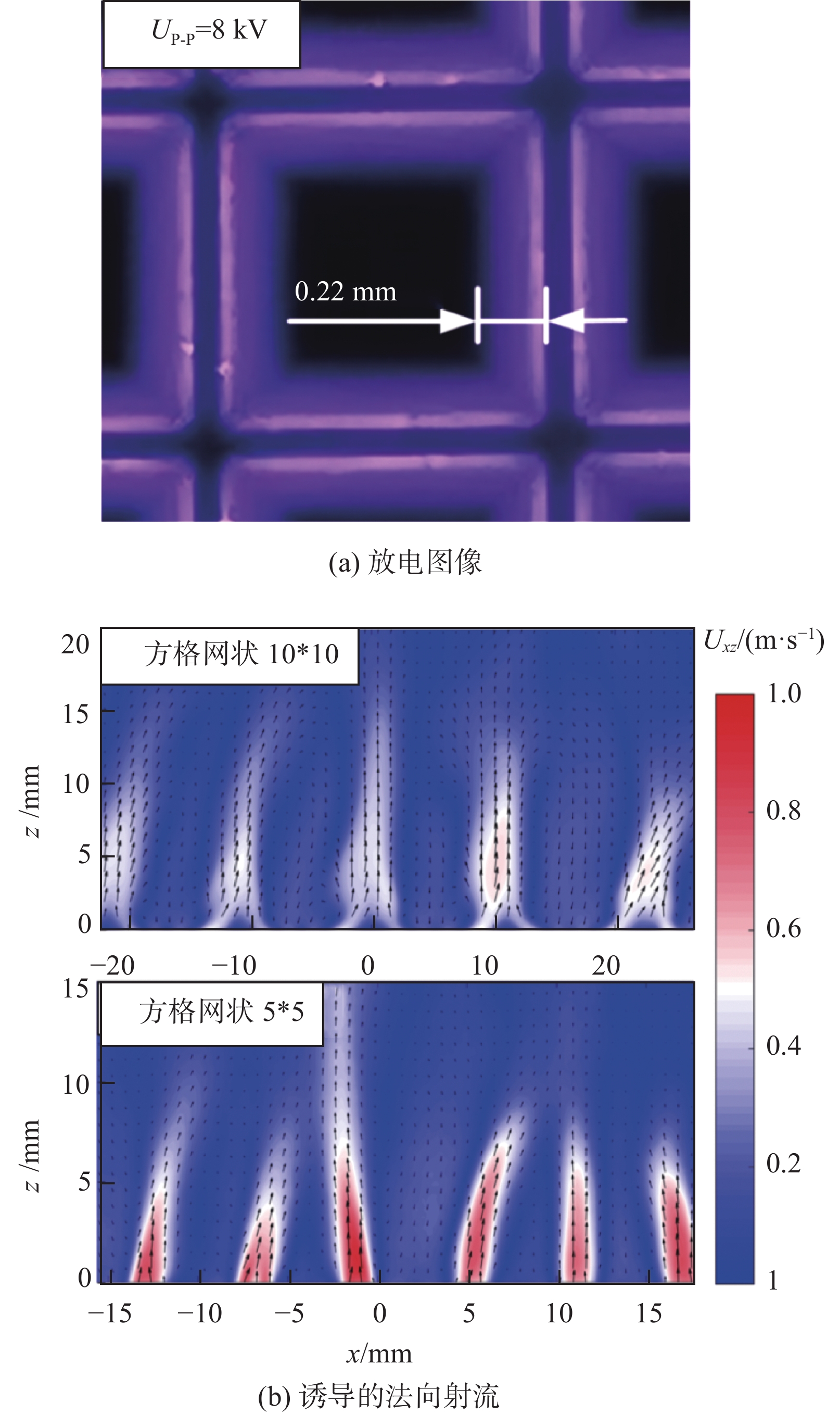
其次,在发展新型等离子体激励方式、创新减阻机理方面,基于等离子体激励的灵活性,可以广泛借鉴其他主/被动湍流减阻方法的作用机理,并采用等离子体激励进行模拟与实现,在现有的等离子体激励产生效益的基础上,创新减阻途径,实现提高减阻效能的目的。例如,可以通过设计方格网状的裸露电极,通过方格电极四周向中央放电的对冲作用,产生法向射流,模拟微吹气减阻的作用效果,如图23所示;或通过设计小型的环形电极单元,模拟粗糙元或壁面凹坑的作用效果,以期进一步提高等离子体湍流减阻效益。
6.2 应用环境:面向高雷诺数强逆压梯度气流环境进行拓展
当前,绝大多数的等离子体湍流减阻研究均在理想的零压力梯度平板湍流边界层(ZPGTBL)中进行,但在飞机的实际飞行中,由于弯曲型面与飞行迎角的存在,湍流边界层均面临强烈且复杂的压力梯度,上述ZPGTBL的理想情况几乎不存在。在实际飞行条件下,受压力梯度带来的黏性尺度与湍流脉动变化等因素的影响,等离子体湍流减阻效果将有所降低[77]。此外,除基于脉冲直流放电的研究外,大多数等离子体湍流减阻研究均以探寻机理为目标,所采用的来流速度仅为O(1 m/s)量级,与实际工程应用相差甚远。因此,面向高雷诺数、强逆压梯度气流环境的研究是等离子体湍流减阻技术走向应用前的必经之路。在复杂压力梯度条件下如何提高湍流减阻效果?在巡航迎角工况的翼型或机翼上,等离子体激励对各部分阻力(摩擦阻力、压差阻力等)的影响如何?这些是亟待回答的问题。
针对翼型减阻问题,文献[74-75]进行了一定的探索,验证了等离子体激励在巡航迎角工况下有效减小翼型总阻力的能力,并阐明了无量纲参数影响规律,证明了等离子体湍流减阻方法在翼型流场等较复杂情况下的应用前景,但等离子体激励对各部分阻力的影响还需进一步研究,作用机理也需进一步揭示。为提高等离子体激励在压力梯度条件下的作用效果,可以根据湍流边界层黏性尺度的变化,适应性地改变等离子体激励的空间尺度,始终保证二者的匹配关系,进而实现更高效的减阻。
6.3 控制策略:由开环控制向智能自适应发展
与展向壁面振荡、吹/吸气等主动湍流减阻方法不同,等离子体湍流减阻方法是基于电信号的方法,具有响应快、控制灵活等优点。在当今人工智能与控制技术飞速发展的时代,将以往等离子体湍流减阻中的开环控制向智能自适应控制发展,能够充分发挥等离子体减阻技术的优势,提高减阻效能,是必然的发展趋势。
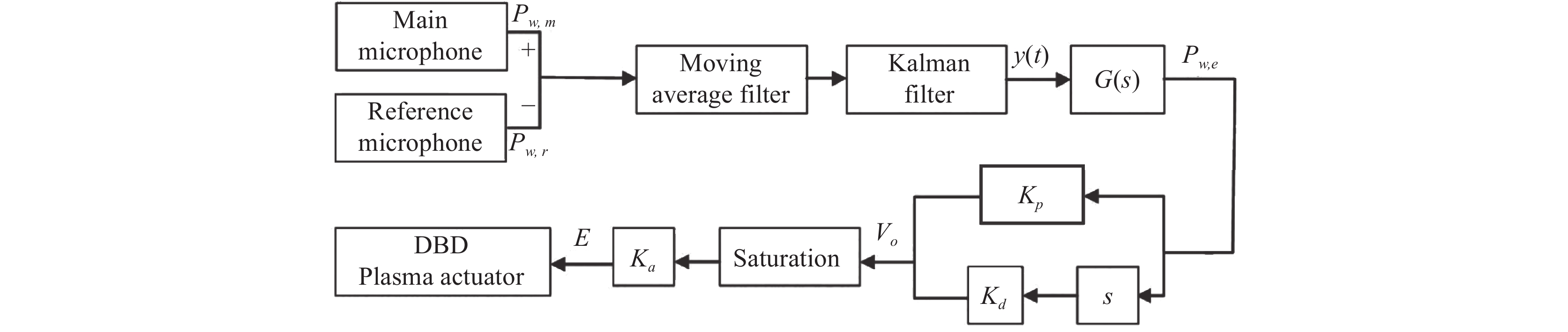
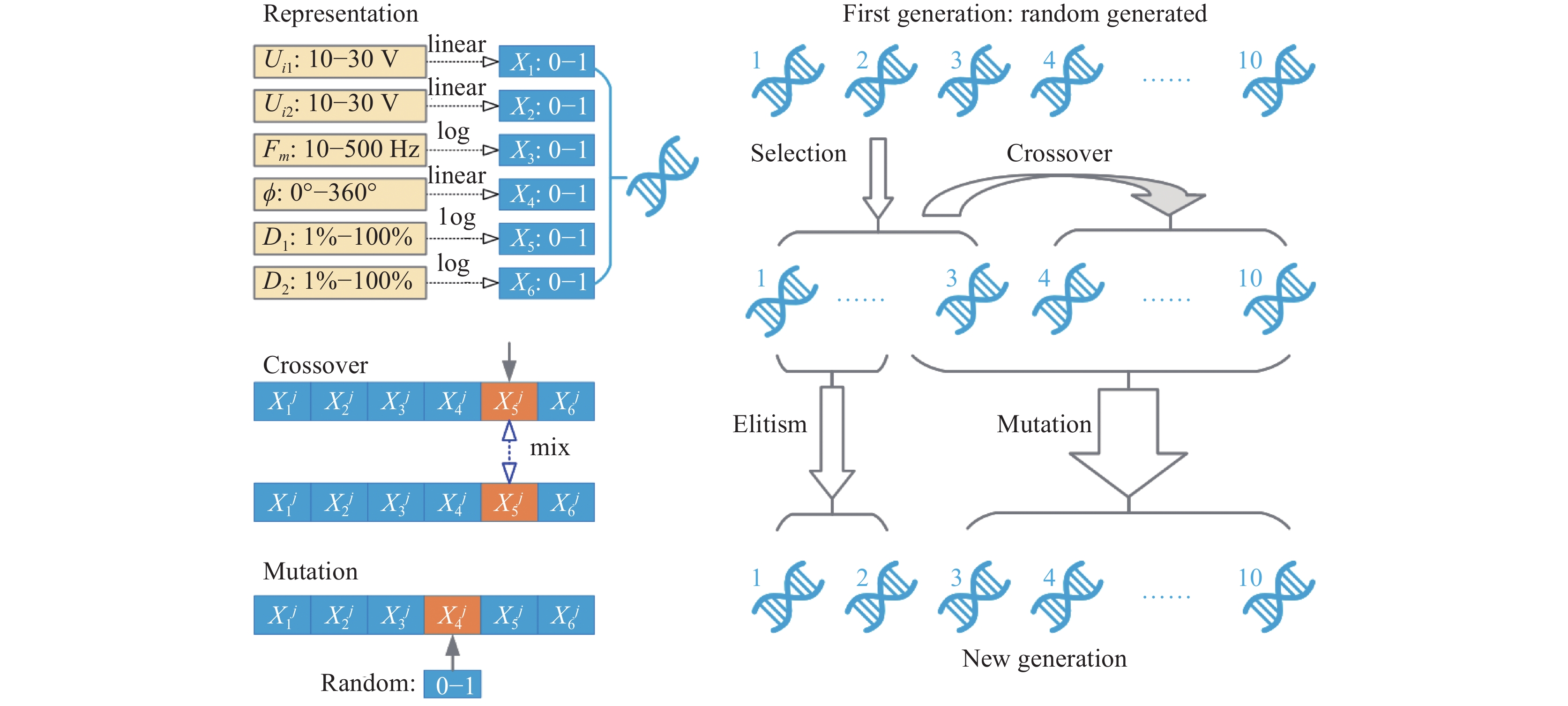
目前,研究者们已对采用自适应控制方法优化等离子体湍流减阻效果进行了初步探索。文献[103]将如图24所示的前馈比例微分控制系统引入湍流减阻的控制与优化中,保证系统以最佳方案对激励器放电电压进行调节,在几乎不影响减阻效果的基础上,使放电功率减小30%,图中G(s)表示经过滤波后的脉动压力信号y(t)的拉普拉斯变换。文献[119]基于遗传算法(如图25)与代理模型等多种方法,对振荡放电等离子体激励的电压、频率、相位、占空比等多个参数进行智能优化,实现了40%的减阻效果,能量效益也得到极大提升。上述工作是控制与优化算法在等离子体湍流减阻上的初步应用。
后续,等离子体湍流减阻方法向智能自适应发展的重点是:基于人工智能方法(如深度强化学习等),进一步对控制参数与策略进行优化,形成适应变化流动场景的高效益减阻激励控制律,实现等离子体湍流减阻的自适应控制。等离子体湍流减阻在智能流体力学领域的发展以及人工智能技术的引入,将使等离子体湍流减阻技术焕发出更大的活力。
7. 结 论
等离子体激励具有结构简单、响应快、易于智能控制等众多优点,将等离子体激励应用于飞机湍流摩擦减阻中,受到广泛关注。
1)按照等离子体激励特性及其与来流的相互关系,等离子体湍流减阻方法可分为展向非定常、展向定常、流向定常激励等类型。从研究历程看,初期研究主要集中在展向非定常激励,后将激励简化为展向与流向定常激励。
2)在平板湍流边界层中,等离子体激励主要通过诱导大尺度流向涡,产生输运作用,减小摩擦阻力,其能使摩擦阻力减小40%以上;在摩擦阻力主导的巡航迎角工况下的翼型上,激励同样能在20 m/s的来流速度下使翼型总阻力减小13.7%,但离实际应用还有一定差距,具体减阻构成与作用机理尚需实验验证。
3)为将等离子体湍流减阻技术向应用拓展,需要发展新型高效能等离子体减阻激励方法,面向高雷诺数、强逆压梯度气流环境进行适应性拓展研究,提高等离子体激励的产生效率,探索新型减阻机理,研究等离子体激励对翼型、机翼及整机阻力的综合影响及其机理,提高总体减阻能量效益。
4)在人工智能应用快速发展的现今时代,等离子体激励作为纯电驱动的流动控制方法,具有响应快、控制灵活等优点,与其他流动控制方法相比,能够更加便利地与人工智能技术相结合,进一步优化控制参数与控制策略,实现减阻自适应控制,使等离子体湍流减阻焕发更大的生机与活力。
-
表 1 不同等离子体湍流减阻方法的代表性实验减阻效果
Table 1 Representative experimental results of different plasma-based turbulent drag reduction methods
方法分类 高压波形 工作模式 研究对象 减阻效果 Reτ或Rec 来流速度/(m·s–1) 非定常方法 高压正弦波 展向振荡激励 零压梯度平板 >45% 475 1.75 [71] 展向行波激励 零压梯度平板 45% 475 1.75[71] 定常方法 高压正弦波 展向单侧激励 零压梯度平板 10% 572 2.4 [72] 展向对冲激励 零压梯度平板 26% 572 2.4[72] 展向对冲激励 翼型 - 2.07×106 170[73] 展向单侧激励 翼型 64% 4.97×104 5[74] 展向单侧激励 翼型 13.7% 1.99×105 20[74] 流向定常激励 零压梯度平板 65.1% - ≈ 4.5[52-53] 脉冲直流 展向单侧激励 零压梯度平板 - - 2.5[75] 展向单侧激励 零压梯度平板 >70% ≈ 2014 17.4[76] 展向单侧激励 零压梯度平板 ≈ 18% ≈ 4508 52.1[76] 展向单侧激励 逆压梯度平板 42% - 27.1[77] 展向对冲激励 零压梯度平板 ≈ 68% ≈ 4106 17.4[76] 展向对冲激励 零压梯度平板 ≈16% ≈ 6856 34.7[76] -
[1] 马汉东, 崔尔杰. 大型飞机阻力预示与减阻研究[J]. 力学与实践, 2007, 29(2): 1-8. MA H D, CUI E J. Drag prediction and reduction for civil transportation aircraft[J]. Mechanics in Engineering, 2007, 29(2): 1-8. (in Chinese)
[2] 刘沛清, 张雯, 郭昊. 大型运输机的减阻技术[J]. 力学与实践, 2018, 40(2): 129-139, 154. LIU P Q, ZHANG W, GUO H. Drag reduction technique for large transport aircraft[J]. Mechanics in Engineering, 2018, 40(2): 129-139, 154. . DOI: 10.6052/1000-0879-17-295(in Chinese)
[3] THIBERT J J, RENEAUX J, SCHMITT V. ONERA activities on drag reduction[C]//17th Conference of ICAS, 1990.
[4] GAD-EL-HAK M. Flow control: the future[J]. Journal of Aircraft, 2001, 38(3): 402-418. DOI: 10.2514/2.2796
[5] PRANDTL L. Uber flussigkeitsbewegung bei sehr kleiner reibung[C]//3rd International Math Congress, 1904: 484–491. https://www.damtp.cam.ac.uk/user/tong/fluids/prandtl.pdf
[6] JOSLIN R D, MILLER D N. Fundamentals and applications of modern flow control[M]. American Institute of Aeronautics and Astronautics, 2009
[7] LIN J C. Review of research on low-profile vortex generators to control boundary-layer separation[J]. Progress in Aerospace Sciences, 2002, 38(4-5): 389-420. DOI: 10.1016/S0376-0421(02)00010-6
[8] GREENBLATT D, WYGNANSKI I J. The control of flow separation by periodic excitation[J]. Progress in Aerospace Sciences, 2000, 36(7): 487-545. DOI: 10.1016/s0376-0421(00)00008-7
[9] 吴云, 李应红. 等离子体流动控制研究进展与展望[J]. 航空学报, 2015, 36(2): 381-405. WU Y, LI Y H. Progress and outlook of plasma flow control[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(2): 381-405. (in Chinese)
[10] ANDERSON J D. Fundamentals of aerodynamics[M]. New York: McGraw-Hill, 2011.
[11] 张永升, 刘丹, 郎卫东. 后体参数对运输机后体阻力的影响[J]. 力学季刊, 2013, 34(4): 585-590. DOI: 10.3969/j.issn.0254-0053.2013.04.010(in Chinese) ZHANG Y S, LIU D, LANG W D. Effects of geometry parameters on drag about afterbodies of transport aircraft[J]. Chinese Quarterly of Mechanics, 2013, 34(4): 585-590. doi: 10.3969/j.issn.0254-0053.2013.04.010
[12] MOHSEN J. Aircraft drag reduction: an overview[R]. Chalmers University of Technology, 2011. https://www.researchgate.net/publication/235339328_Aircraft_Drag_Reduction_An_Overview
[13] BUSHNELL D M. Aircraft drag reduction—a review[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2003, 217(1): 1-18. DOI: 10.1243/095441003763031789
[14] SCHUELE C Y, CORKE T C, MATLIS E. Control of stationary cross-flow modes in a Mach 3.5 boundary layer using patterned passive and active roughness[J]. Journal of Fluid Mechanics, 2013, 718: 5-38. DOI: 10.1017/jfm.2012.579
[15] KLINE S J, REYNOLDS W C, SCHRAUB F A, et al. The structure of turbulent boundary layers[J]. Journal of Fluid Mechanics, 1967, 30(4): 741-773. DOI: 10.1017/s0022112067001740
[16] WALSH M J. Riblets as a viscous drag reduction technique[J]. AIAA Journal, 1983, 21(4): 485-486. DOI: 10.2514/3.60126
[17] VAN NESSELROOIJ M, VELDHUIS L M, VAN OUDHEUSDEN B W, et al. Drag reduction by means of dimpled surfaces in turbulent boundary layers[J]. Experiments in Fluids, 2016, 57(9): 142. DOI: 10.1007/s00348-016-2230-9
[18] CHOI K S, YANG X, CLAYTON B R, et al. Turbulent drag reduction using compliant surfaces[J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 1997, 453(1965): 2229-2240. DOI: 10.1098/rspa.1997.0119
[19] KIM K, SUNG H J. Effects of periodic blowing from spanwise slot on a turbulent boundary layer[J]. AIAA Journal, 2003, 41(10): 1916-1924. DOI: 10.2514/2.1907
[20] ANTONIA R A, ZHU Y, SOKOLOV M. Effect of concentrated wall suction on a turbulent boundary layer[J]. Physics of Fluids, 1995, 7(10): 2465-2474. DOI: 10.1063/1.868690
[21] BARON A, QUADRIO M. Turbulent drag reduction by spanwise wall oscillations[J]. Applied Scientific Research, 1995, 55(4): 311-326. DOI: 10.1007/BF00856638
[22] CHOI K S. Near-wall structure of turbulent boundary layer with spanwise-wall oscillation[J]. Physics of Fluids, 2002, 14(7): 2530-2542. DOI: 10.1063/1.1477922
[23] CORKE T C, ENLOE C L, WILKINSON S P. Dielectric barrier discharge plasma actuators for flow control[J]. Annual Review of Fluid Mechanics, 2010, 42: 505-529. DOI: 10.1146/annurev-fluid-121108-145550
[24] LI Y H, WU Y, LI J. Review of the investigation on plasma flow control in China[J]. International Journal of Flow Control, 2012, 4(1-2): 1-18. DOI: 10.1260/1756-8250.4.1-2.1
[25] POPE S B. Turbulent flows[M]. Cambridge: Cambridge University Press, 2000
[26] 许春晓. 壁湍流相干结构和减阻控制机理[J]. 力学进展, 2015, 45(1): 111-140. doi: 10.6052/1000-0992-15-006 XU C X. Coherent structures and drag-reduction mechanism in wall turbulence[J]. Advances in Mechanics, 2015, 45(1): 111-140. (in Chinese) doi: 10.6052/1000-0992-15-006
[27] ROBINSON S K. Coherent motions in the turbulent boundary layer[J]. Annual Review of Fluid Mechanics, 1991, 23: 601-639. DOI: 10.1146/annurev.fl.23.010191.003125
[28] CORKE T C, THOMAS F O. Active and passive turbulent boundary-layer drag reduction[J]. AIAA Journal, 2018, 56(10): 3835-3847. DOI: 10.2514/1.j056949
[29] SOLEIMANI S, ECKELS S. A review of drag reduction and heat transfer enhancement by riblet surfaces in closed and open channel flow[J]. International Journal of Thermofluids, 2021, 9: 100053. DOI: 10.1016/j.ijft.2020.100053
[30] WALSH M. Turbulent boundary layer drag reduction using riblets[C]//20th Aerospace Sciences Meeting, Orlando, FL, USA. Reston, Virigina: AIAA, 1982. doi: 10.2514/6.1982-169
[31] 李山, 姜楠, 杨绍琼. 正弦波沟槽对湍流边界层相干结构影响的TR-PIV实验研究[J]. 物理学报, 2019, 68(7): 074702. DOI: 10.7498/aps.68.20181875(in Chinese) LI S, JIANG N, YANG S Q. Influence of sinusoidal riblets on the coherent structures in turbulent boundary layer studied by time-resolved particle image velocimetry[J]. Acta Physica Sinica, 2019, 68(7): 074702. doi: 10.7498/aps.68.20181875
[32] 杨绍琼. 壁湍流相干结构及其沟槽被动控制的PIV实验研究[D]. 天津: 天津大学, . [33] CHOI H, MOIN P, KIM J. Active turbulence control for drag reduction in wall-bounded flows[J]. Journal of Fluid Mechanics, 1994, 262: 75-110. DOI: 10.1017/s0022112094000431
[34] HAMMOND E P, BEWLEY T R, MOIN P. Observed mechanisms for turbulence attenuation and enhancement in opposition-controlled wall-bounded flows[J]. Physics of Fluids, 1998, 10(9): 2421-2423. DOI: 10.1063/1.869759
[35] CHUNG Y M, TALHA T. Effectiveness of active flow control for turbulent skin friction drag reduction[J]. Physics of Fluids, 2011, 23(2): 025102. DOI: 10.1063/1.3553278
[36] 范云涛, 张阳, 叶志贤, 等. 微吹气对湍流平板边界层流动特性的影响及其减阻机理[J]. 航空学报, 2020, 41(10): 123814. FAN Y T, ZHANG Y, YE Z X, et al. Micro-blowing: effect on flow characteristics in turbulent flat plate boundary layer and drag reduction mechanism[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(10): 123814(in Chinese)
[37] TILLMAN T, HWANG D. Drag reduction on a large-scale nacelle using a micro-blowing technique[C]//37th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. Reston, Virigina: AIAA, 1999. doi: 10.2514/6.1999-130
[38] HWANG D, HWANG D. A proof of concept experiment for reducing skin friction by using a micro-blowing technique[C]//35th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. Reston, Virigina: AIAA, 1997. doi: 10.2514/6.1997-546
[39] BRADSHAW P, PONTIKOS N S. Measurements in the turbulent boundary layer on an ‘infinite’ swept wing[J]. Journal of Fluid Mechanics, 1985, 159: 105. DOI: 10.1017/s0022112085003123
[40] DRIVER D M, HEBBAR S K. Experimental study of a three-dimensional, shear-driven, turbulent boundary layer[J]. AIAA Journal, 1987, 25(1): 35-42. DOI: 10.2514/3.9575
[41] SENDSTAD O. The near-wall mechanics of three-dimensional turbulent boundary layers[D]. Stanford, CA, USA: Stanford University, 1992.
[42] EATON J K. Effects of mean flow three dimensionality on turbulent boundary-layer structure[J]. AIAA Journal, 1995, 33(11): 2020-2025. DOI: 10.2514/3.12942
[43] QUADRIO M, RICCO P. Critical assessment of turbulent drag reduction through spanwise wall oscillations[J]. Journal of Fluid Mechanics, 2004, 521: 251-271. DOI: 10.1017/s0022112004001855
[44] CHOI K S, CLAYTON B R. The mechanism of turbulent drag reduction with wall oscillation[J]. International Journal of Heat and Fluid Flow, 2001, 22(1): 1-9. DOI: 10.1016/S0142-727X(00)00070-9
[45] KUSHAL K. Spanwise wall oscillation as a drag reduction technique[D]. Delft University of Technology, 2019.
[46] CHIN C, ÖRLÜ R, MONTY J, et al. Simulation of a large-eddy-break-up device (LEBU) in a moderate Reynolds number turbulent boundary layer[J]. Flow, Turbulence and Combustion, 2017, 98(2): 445-460. DOI: 10.1007/s10494-016-9757-y
[47] KIM J S, HWANG J, YOON M, et al. Influence of a large-eddy breakup device on the frictional drag in a turbulent boundary layer[J]. Physics of Fluids, 2017, 29(6): 065103. DOI: 10.1063/1.4984602
[48] CORKE T C, GUEZENNEC Y, NAGIB H M. . Modification in drag of turbulent boundary layers resulting from manipulation of large-scale structures[R]. NASA-CR-3444. https://ntrs.nasa.gov/api/citations/19810021850/downloads/19810021850.pdf
[49] KLIMOV A I, KOBLOV A N, MISHIN G I, et al. Shock wave propagation in a glow discharge[J]. Technical Physics Letters, 1982, 8: 192–194.
[50] MEYER R, PALM P, PLÖNJES E, et al. The effect of a nonequilibrium RF discharge plasma on a conical shock wave in a M = 2.5 flow[C]//32nd AIAA Plasmadynamics and Lasers Conference. doi: 10.2514/6.2001-3059
[51] 李应红, 吴云, 梁华, 等. 等离子体激励气动力学探索与展望[J]. 力学进展, 2022, 52(1): 1-32. LI Y H, WU Y, LIANG H, et al. Exploration and outlook of plasma-actuated gas dynamics[J]. Advances in Mechanics, 2022, 52(1): 1-32. (in Chinese)
[52] ROTH J R, SHERMAN D M, WILKINSON S P. Electrohydrodynamic flow control with a glow-discharge surface plasma[J]. AIAA Journal, 2000, 38: 1166-1172. DOI: 10.2514/3.14531
[53] ROTH J R, SHERMAN D M, WILKINSON S. Boundary layer flow control with a one atmosphere uniform glow discharge surface plasma[C]//36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. Reston, Virigina: AIAA, 1998. doi: 10.2514/6.1998-328
[54] 武占成, 张希军, 胡有志. 气体放电[M]. 北京: 国防工业出版社, 2012. [55] ROUPASSOV D V, NIKIPELOV A A, NUDNOVA M M, et al. Flow separation control by plasma actuator with nanosecond pulsed-periodic discharge[J]. AIAA Journal, 2009, 47(1): 168-185. DOI: 10.2514/1.38113
[56] BENARD N, MOREAU E. EHD force and electric wind produced by plasma actuators used for airflow control[C]//6th AIAA Flow Control Conference, New Orleans, Louisiana, 2012. doi: 10.2514/6.2012-3136
[57] BENARD N, MOREAU E. Electrical and mechanical characteristics of surface AC dielectric barrier discharge plasma actuators applied to airflow control[J]. Experiments in Fluids, 2014, 55(11): 1846. DOI: 10.1007/s00348-014-1846-x
[58] ZHU Y F, WU Y, CUI W, et al. Modelling of plasma aerodynamic actuation driven by nanosecond SDBD discharge[J]. Journal of Physics D: Applied Physics, 2013, 46(35): 355205. DOI: 10.1088/0022-3727/46/35/355205
[59] WU Y. Nanosecond pulsed discharge plasma actuation: characteristics and flow control performance[C]//45th AIAA Plasmadynamics and Lasers Conference, Atlanta, GA. Reston, Virginia: AIAA, 2014. doi: 10.2514/6.2014-2118
[60] BENARD N, ZOUZOU N, CLAVERIE A, et al. Optical visualization and electrical characterization of fast-rising pulsed dielectric barrier discharge for airflow control applications[J]. Journal of Applied Physics, 2012, 111(3): 033303. DOI: 10.1063/1.3682568
[61] TAKASHIMA K, ZUZEEK Y, LEMPERT W R, et al. Characterization of a surface dielectric barrier discharge plasma sustained by repetitive nanosecond pulses[J]. Plasma Sources Science and Technology, 2011, 20(5): 055009. DOI: 10.1088/0963-0252/20/5/055009
[62] DEBIEN A, BENARD N, MOREAU E. Streamer inhibition for improving force and electric wind produced by DBD actuators[J]. Journal of Physics D: Applied Physics, 2012, 45(21): 215201. DOI: 10.1088/0022-3727/45/21/215201
[63] 梁华. 翼型等离子体流动控制研究[D]. 空军工程大学, 2009. LIANG H. Airfoil flow control by plasma actuation[D]. Air Force Engineering University, 2009 (in Chinese).
[64] 赵光银. 翼型/三角翼等离子体冲击流动控制机理研究[D]. 空军工程大学, 2015. ZHAO G Y. Mechanism investigation of airfoil/delta wing plasma-shock-based flow control[D]. Air Force Engineering University, 2015 (in Chinese).
[65] CUI Y D, ZHAO Z J, ZHENG J G, et al. Separation control over a NACA0015 airfoil using nanosecond pulsed plasma actuator[C]//55th AIAA Aerospace Sciences Meeting, Grapevine, Texas. Reston, Virginia: AIAA, 2017. doi: 10.2514/6.2017-0715
[66] DURASIEWICZ C, SINGH A, LITTLE J C. A comparative flow physics study of NS-DBD vs AC-DBD plasma actuators for transient separation control on a NACA0012 airfoil[C]//2018 AIAA Aerospace Sciences Meeting, Kissimmee, Florida. Reston, Virginia: AIAA, 2018. doi: 10.2514/6.2018-1061
[67] LIKHANSKII A, SHNEIDER M, OPAITS D, et al. Limitations of the DBD effects on the external flow[C]//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, Florida. Reston, Virigina: AIAA, 2010. doi: 10.2514/6.2010-470
[68] KELLEY C L, BOWLES P O, COONEY J, et al. Leading-edge separation control using alternating-current and nanosecond-pulse plasma actuators[J]. AIAA Journal, 2014, 52(9): 1871-1884. DOI: 10.2514/1.j052708
[69] 张鑫, 黄勇, 阳鹏宇, 等. 等离子体无人机失速分离控制飞行试验[J]. 航空学报, 2018, 39(2): 121587. ZHANG X, HUANG Y, YANG P Y, et al. Flight test of flow separation control using plasma UAV[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(2): 121587(in Chinese).
[70] SU Z, LI J, LIANG H, et al. UAV flight test of plasma slats and ailerons with microsecond dielectric barrier discharge[J]. Chinese Physics B, 2018, 27(10): 105205. DOI: 10.1088/1674-1056/27/10/105205
[71] CHOI K S, JUKES T, WHALLEY R. Turbulent boundary-layer control with plasma actuators[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2011, 369(1940): 1443-1458. DOI: 10.1098/rsta.2010.0362
[72] CHENG X Q, WONG C W, HUSSAIN F, et al. Flat plate drag reduction using plasma-generated streamwise vortices[J]. Journal of Fluid Mechanics, 2021, 918: A24. DOI: 10.1017/jfm.2021.311
[73] LI Y Q, GAO C, WU B, et al. Turbulent boundary layer control with a spanwise array of DBD plasma actuators[J]. Plasma Science and Technology, 2021, 23(2): 025501. DOI: 10.1088/2058-6272/abce0d
[74] SU Z, ZONG H H, LIANG H, et al. Minimizing airfoil drag at low angles of attack with DBD-based turbulent drag reduction methods[J]. Chinese Journal of Aeronautics, 2023, 36(4): 104-119. DOI: 10.1016/j.cja.2022.11.019
[75] 苏志. 展向阵列等离子体激励调控平板/翼型摩擦阻力的方法和机理研究[D]. 空军工程大学, 2022. SU Z. Method and mechanism investigation of flat plate/airfoil friction drag reduction by spanwise plasma actuation array[D]. Air Force Engineering University, 2022 (in Chinese).
[76] THOMAS F O, CORKE T C, DUONG A, et al. Turbulent drag reduction using pulsed-DC plasma actuation[J]. Journal of Physics D: Applied Physics, 2019, 52(43): 434001. DOI: 10.1088/1361-6463/ab3388
[77] YATES K, CORKE T, THOMAS F, et al. Viscous drag reduction in adverse pressure gradient boundary layers[C]//AIAA Scitech 2019 Forum, San Diego, California. Reston, Virginia: AIAA, 2019. doi: 10.2514/6.2019-0309
[78] JUNG W J, MANGIAVACCHI N, AKHAVAN R. Suppression of turbulence in wall-bounded flows by high-frequency spanwise oscillations[J]. Physics of Fluids A: Fluid Dynamics, 1992, 4(8): 1605-1607. DOI: 10.1063/1.858381
[79] DU Y Q, KARNIADAKIS G E. Suppressing wall turbulence by means of a transverse traveling wave[J]. Science, 2000, 288(5469): 1230. DOI: 10.1126/science.288.5469.1230
[80] DU Y Q, SYMEONIDIS V, KARNIADAKIS G E. Drag reduction in wall-bounded turbulence via a transverse travelling wave[J]. Journal of Fluid Mechanics, 2002, 457: 1-34. DOI: 10.1017/s0022112001007613
[81] KARNIADAKIS G E, CHOI K S. Mechanisms on transverse motions in turbulent wall flows[J]. Annual Review of Fluid Mechanics, 2003, 35: 45-62. DOI: 10.1146/annurev.fluid.35.101101.161213
[82] WILKINSON S P. Investigation of an oscillating surface plasma for turbulent drag reduction[C]//41st Aerospace Sciences Meeting and Exhibit, Reno, N , 2003. AIAA 2003-1023. https://ntrs.nasa.gov/api/citations/20030004240/downloads/20030004240.pdf
[83] HEHNER M T, GATTI D, KRIEGSEIS J. Stokes-layer formation under absence of moving parts—a novel oscillatory plasma actuator design for turbulent drag reduction[J]. Physics of Fluids, 2019, 31(5): 051701. DOI: 10.1063/1.5094388
[84] HEHNER M T, GATTI D, MATTERN P, et al. Virtual wall oscillations forced by a DBD plasma actuator operating under beat frequency - a concept for turbulent drag reduction[C]//AIAA Aviation 2020 Forum, Virtual Event. Reston, Virginia: AIAA, 2020. doi: 10.2514/6.2020-2956
[85] JUKES T, CHOI K S, JOHNSON G, et al. Turbulent drag reduction by surface plasma through spanwise flow oscillation[C]//3rd AIAA Flow Control Conference, San Francisco, California. Reston, Virigina: AIAA, 2006. doi: 10.2514/6.2006-3693
[86] ELAM D. A direct numerical simulation of dielectric barrier discharge (DBD) plasma actuators for turbulent skin-friction control[D]. Coventry, West Midlands, UK: University of Warwick, 2012.
[87] SHYY W, JAYARAMAN B, ANDERSSON A. Modeling of glow discharge-induced fluid dynamics[J]. Journal of Applied Physics, 2002, 92(11): 6434-6443. DOI: 10.1063/1.1515103
[88] ALTıNTAŞ A, DAVIDSON L, PENG S H. Direct numerical simulation of drag reduction by spanwise oscillating dielectric barrier discharge plasma force[J]. Physics of Fluids, 2020, 32(7): 075101. doi: 10.1063/5.0007103 https://publications.lib.chalmers.se/records/fulltext/245839/local_245839.pdf
[89] MAHFOZE O, LAIZET S. Skin-friction drag reduction in a channel flow with streamwise-aligned plasma actuators[J]. International Journal of Heat and Fluid Flow, 2017, 66: 83-94. DOI: 10.1016/j.ijheatfluidflow.2017.05.013
[90] ALESSIO M. DNS study of turbulent drag reduction via DBD plasma actuators[D]. Politecnico di Milano, 2020.
[91] SU Z, ZONG H H, LIANG H, et al. Optimization in frequency characteristics of an oscillating dielectric barrier discharge plasma actuator[J]. Sensors and Actuators A: Physical, 2023, 351: 114195. DOI: 10.1016/j.sna.2023.114195
[92] WHALLEY R D, CHOI K S. The starting vortex in quiescent air induced by dielectric-barrier-discharge plasma[J]. Journal of Fluid Mechanics, 2012, 703: 192-203. DOI: 10.1017/jfm.2012.206
[93] WHALLEY R D. Turbulent boundary-layer control with DBD plasma actuators using spanwise travelling-wave technique[D]. Nottingham, East Midlands, UK: The University of Nottingham, 2011.
[94] WHALLEY R D, CHOI K S. Turbulent boundary-layer control with spanwise travelling waves[J]. Journal of Physics: Conference Series, 2011, 318(2): 022039. DOI: 10.1088/1742-6596/318/2/022039
[95] WHALLEY R D, CHOI K S. Turbulent boundary-layer control with plasma spanwise travelling waves[J]. Experiments in Fluids, 2014, 55(8): 1796. DOI: 10.1007/s00348-014-1796-3
[96] HUANG L P, CHOI K S, FAN B C. Formation of low-speed ribbons in turbulent channel flow subject to a spanwise travelling wave[J]. Journal of Physics: Conference Series, 2011, 318(2): 022027. DOI: 10.1088/1742-6596/318/2/022027
[97] ZHAO H, WU J Z, LUO J S . Turbulent drag reduction by traveling wave of flexible wall[J]. Fluid Dynamics Research, 2004, 34(3): 175-198. DOI: 10.1016/j.fluiddyn.2003.11.001
[98] ZONG H H, SU Z, LIANG H, et al. Experimental investigation and reduced-order modeling of plasma jets in a turbulent boundary layer for skin-friction drag reduction[J]. Physics of Fluids, 2022, 34(8): 085133. DOI: 10.1063/5.0104609
[99] LI Y P, WONG C W, LI Y Z, et al. Drag reduction of a turbulent boundary layer using plasma actuators[C]//19th Australasian Fluid Mechanics Conference, Melbourne, Australia, 2014.https://people.eng.unimelb.edu.au/imarusic/proceedings/19/340.pdf
[100] WONG C W, ZHOU Y, LI Y Z, et al. Active drag reduction in a turbulent boundary layer based on plasma-actuator-generated streamwise vortices[C]//9th International Symposium on Turbulence and Shear Flow Phenomena, Melbourne, Australia, 2015. http://www.tsfp-conference.org/proceedings/2015/v3/9A-5.pdf
[101] 彭倩. 基于等离子体激励器控制湍流边界层减阻的参数优化研究[D]. 哈尔滨: 哈尔滨工业大学, 2018. [102] WONG C W, X Q CHENG, Q PENG, et al. Effects of plasma-actuator-generated vortices on a turbulent boundary layer[R]. 10th International Symposium on Turbulence and Shear Flow Phenomena, Chicago, USA, 2017.
[103] WONG C W, CHENG X Q, FAN D W, et al. Friction drag reduction based on a proportional-derivative control scheme[J]. Physics of Fluids, 2021, 33(7): 075115. DOI: 10.1063/5.0056169
[104] 郑海波, 高超, 武斌, 等. 基于等离子体激励的湍流边界层减阻控制[J]. 航空动力学报, 2023, 38(5): 1157-1165. ZHENG H B, GAO C, WU B, et al. Drag reduction control of turbulent boundary layer based on plasma actuation[J]. Journal of Aerospace Power, 2023, 38(5): 1157-1165. (in Chinese)
[105] MCGOWEN R, CORKE T C, MATLIS E H, et al. Pulsed-DC plasma actuator characteristics and application in compressor stall control[C]//54th AIAA Aerospace Sciences Meeting, San Diego, California, USA. Reston, Virginia: AIAA, 2016. doi: 10.2514/6.2016-0394
[106] MURPHY J, LAVOIE P. Characterization of DBD plasma actuators via PIV measurements[C]//51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, Texas. Reston, Virigina: AIAA, 2013. doi: 10.2514/6.2013-346
[107] MCGOWAN R C, CORKE T C, MATLIS E H, et al. Pulsed-DC plasma actuation for stall control in an axial fan[C]//2018 AIAA Aerospace Sciences Meeting, Kissimmee, Florida. Reston, Virginia: AIAA, 2018. doi: 10.2514/6.2018-1357
[108] SONTAG J M, GORDEYEV S, DUONG A, et al. Studies of pulsed-DC plasma actuator and its effect on turbulent boundary layers using novel optical diagnostics[C]//AIAA Scitech 2019 Forum, San Diego, California. Reston, Virginia: AIAA, 2019. doi: 10.2514/6.2019-0468
[109] DUONG A, MIDYA S, CORKE T C, et al. Turbulent boundary layer drag reduction using pulsed-dc plasma actuation[C]//11th International Symposium on Turbulence and Shear Flow Phenomena, Southampton, UK, 2019.
[110] BLACKWELDER R F, KAPLAN R E. On the wall structure of the turbulent boundary layer[J]. Journal of Fluid Mechanics, 1976, 76(1): 89-112. DOI: 10.1017/s0022112076003145
[111] DUONG A H, CORKE T C, THOMAS F O. Characteristics of drag reduced turbulent boundary layers through pulsed-DC actuation[C]//AIAA Scitech 2020 Forum, Orlando, FL. Reston, Virginia: AIAA, 2020. doi: 10.2514/6.2020-0098
[112] DUONG A H, CORKE T C, THOMAS F O. Characteristics of drag-reduced turbulent boundary layers with pulsed-direct-current plasma actuation[J]. Journal of Fluid Mechanics, 2021, 915: A113. DOI: 10.1017/jfm.2021.167
[113] CAIN A B, NELSON C C. Studies of the effects of drag reduction due to plasma actuation applied to aircraft configurations[C]//AIAA Scitech 2019 Forum, San Diego, California. Reston, Virginia: AIAA, 2019. doi: 10.2514/6.2019-2180
[114] NAKAI S, NISHIDA H, OSHIO Y. Investigation on performance characteristics of dielectric discharge plasma actuator using pulsed-dc waveform[J]. Journal of Fluid Science and Technology, 2018, 13(3): JFST0018. DOI: 10.1299/jfst.2018jfst0018
[115] STARIKOVSKIY A Y, ALEKSANDROV N L. Gasdynamic flow control by ultrafast local heating in a strongly nonequilibrium pulsed plasma[J]. Plasma Physics Reports, 2021, 47(2): 148-209. DOI: 10.1134/s1063780x21020069
[116] SU Z, ZONG H H, LIANG H, et al. Effect of pulse width on the characteristics of a dielectric barrier discharge plasma actuator driven by high-voltage pulses[J]. Journal of Physics D: Applied Physics, 2021, 54(33): 33LT02. DOI: 10.1088/1361-6463/ac00f0
[117] SU Z, ZONG H H, LIANG H, et al. Characteristics of a dielectric barrier discharge plasma actuator driven by pulsed-DC high voltage[J]. Journal of Physics D: Applied Physics, 2022, 55(7): 075203. DOI: 10.1088/1361-6463/ac30bc
[118] WU B, GAO C, LIU F, et al. Reduction of turbulent boundary layer drag through dielectric-barrier-discharge plasma actuation based on the Spalding formula[J]. Plasma Science and Technology, 2019, 21(4): 045501. DOI: 10.1088/2058-6272/aaf2e2
[119] ZONG H H, WU Y, LIANG H, et al. Experimental investigation and intelligent optimization of airfoil zero-lift drag reduction with plasma actuators[J]. AIAA Journal, 2023, 61(1): 223-240. DOI: 10.2514/1.j062099
-
期刊类型引用(2)
1. 徐海笑,姜慧,杨永杰,龚子羿,杨帆. 交流激励下的锯齿环状表面介质阻挡放电特性. 高电压技术. 2025(04): 2049-2059 .  百度学术
百度学术
2. 张梦瑶,郑全福,罗林根,盛戈皞,江秀臣. 气隙长度对大气压下环氧树脂阻挡放电的影响研究. 电机与控制学报. 2024(05): 17-26 .  百度学术
百度学术
其他类型引用(1)





 下载:
下载: