Effects of fin installation on pressure fluctuation in a Francis turbine draft tube
-
摘要: 为了抑制混流式水轮机在部分负荷工况下的压力脉动，在尾水管直锥段设置鳍片是一种可取的工程措施。本文基于数值模拟方法细致考察了设置鳍片对混流式水轮机尾水管内部流动及压力脉动的影响。结果表明：鳍通过改变鳍周围的速度和压力分布，并作用于涡的演变过程，进而影响尾水管中的涡带运动和压力脉动。在非空化工况下，鳍表面产生的附鳍小涡带起到稳定压力场的作用，降低了尾水管直锥段的压力脉动；而附鳍小涡带与主流区涡带的相互作用则恶化了尾水管弯肘段的流动，反而使得弯肘段压力脉动略微回升；在空化工况下，尾水管壁面加鳍显著降低涡带规模和空泡体积，使得尾水管的压力脉动得到明显削弱。Abstract: To alleviate pressure fluctuation inside a Francis turbine draft tube working under part-load operation, a fin installed on the wall of the conical part is one effective method in engineering application. This paper investigates the effects of fin installation on the internal flow and pressure fluctuation inside the draft tube based on numerical calculation. Results show that a fin can change the velocity and pressure distribution around the fin. Further, the fin affects the vortex evolution in draft tube and consequently changes vortex rope and pressure fluctuation. Under non-cavitation condition, an extra small vortex rope occurs near the fin, which plays the role of pressure stabilizer and decreases the pressure fluctuation amplitude in the conical part. It is the interaction of the extra small vortex rope with the vortex rope in mainstream results in the complicated flow in the elbow part of the draft tube. As a result, in the elbow, there is a slight increase of pressure fluctuation amplitude. Under cavitation condition, the fin reduces the size of both vortex rope and cavity, and suppresses the pressure fluctuation in the whole draft tube.
-
Keywords:
- draft tube /
- pressure fluctuation /
- fin /
- vortex rope /
- cavitation
-
0. 引言
水力发电作为一种拥有快速响应能力的可再生能源，在电网中通常承担调峰和调频的作用，这意味着水电机组经常需要在偏离设计工况条件下运行。Jacob等[1-2]通过分析大量试验数据，指出当水轮机工作在非设计工况，尤其是部分负荷工况时，水轮机尾水管内会出现强烈的压力脉动。这种压力脉动频率较低，会对水轮机的稳定运行、机组和厂房的安全产生不利影响，因而尾水管压力脉动一直受到工业界和学术界的广泛关注[3]。
自Rheingans[4]在1940年第一次提出水轮机尾水管中压力脉动的问题后，其原因便一直被众多学者关注和讨论。目前学者普遍认为，尾水管在部分负荷工况下出现的压力脉动是由尾水管中出现的螺旋形涡带运动所导致的；涡带的存在使得尾水管横截面上压力分布不均，并且随着涡带的旋转，不对称压力场也在旋转，导致压力随时间周期性变化，形成压力脉动。螺旋形涡带的成因则是部分负荷工况下尾水管入口处的旋流(即速度存在切向分量)。美国垦务局(The US Bureau of Reclamation)[5]为此对尾水管中的旋流进行了实验研究，并对不同旋流度下的涡带形态和行为进行了分析。结果表明只有当旋流度达到一定程度后，尾水管中才会出现螺旋形涡带[5-6]。螺旋形涡带出现在部分负荷工况下，所以只有当水轮机运行相对流量(Q/Qd，Qd为设计点流量)处于0.5和0.85之间时，尾水管中才会出现剧烈的压力脉动。涡带诱发的压力脉动主要成分的频率较低，相当于转轮转动频率的0.2~0.4倍之间，且Q/Qd越小，压力脉动频率越高[1, 7-9]。此外，当空化发生时，涡带内产生的空泡会增大涡带的规模，并使得压力脉动更为剧烈[6]，压力脉动频率也会有所变化[10]。
部分负荷工况下，尾水管中的压力脉动对水电机组的稳定和安全运行可造成极大威胁。为了抑制这种压力脉动，目前已有诸多思路和方法被提出，如在尾水管壁面安装鳍、向尾水管中通气便是其中两种行之有效的措施。Nishi等采用实验和数值方法研究了鳍对尾水管压力脉动的影响，涉及的研究内容包括不同种类鳍的影响[11]、鳍的数目与安装位置的影响[12]等。结果表明鳍的安装可以明显降低涡带的偏心程度，降低压力脉动。Dmitry等[13]也发现，鳍的安装可以使得压力脉动幅值降低30%~40%。而从主轴中心孔向尾水管中通气也是一种有效的抑制压力脉动的方法[14-17]，其原理是通入空气来降低尾水管中横截面上的压力梯度，抑制尾水管中的空化，并减小涡带的偏心程度。此外，Nishi等[18]也曾尝试通过鳍表面上的小孔向尾水管中通气，结果发现，在鳍无法发挥作用的工况下，这种方式可以抑制压力脉动，而且需要的空气量很小。
参考Nishi等[18]的思路，本研究着眼于考察加鳍对部分负荷工况下尾水管中压力脉动的抑制效果，并详细讨论水轮机内部流场和空化的演化。
1. 数值方法
1.1 水轮机模型和鳍
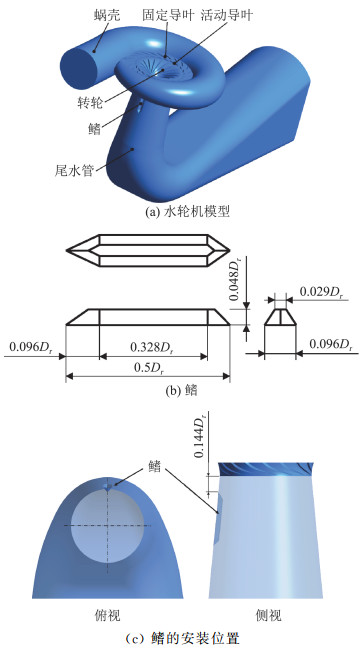
数值计算中使用的水轮机模型如图 1(a)所示，主要流动部件包括蜗壳、固定导叶、活动导叶、转轮和尾水管，水轮机模型的主要几何参数见表 1。鳍安装在尾水管直锥段的内壁。鳍的安装位置及几何尺寸依据参考文献[11, 12]确定，如图 1(b)、(c)所示。
表 1 水轮机几何参数Table 1. Geometric parameters of the Francis turbine参数 数值 转轮进口直径Dr/mm 420 转轮叶片数Zb 17 活动导叶数 24 固定导叶数 23 导叶相对高度b0=b/Dr 0.183 在部分负荷工况下水轮机的主要运行参数如表 2所示。其中运行水头为30.07 m，流量为266.1 L/s，相对流量比为0.724(相对于设计流量)。同时，为了分别探究非空化和空化工况下鳍的作用，选择了两种空化工况进行计算，其空化数分别为0.12(非空化工况)和0.04(空化工况)。空化数的计算如下：
σ=pout−pv−ρgHSρgH (1) 表 2 水轮机运行参数Table 2. Operating parameters of the Francis turbine参数 数值 活动导叶开度α0/mm 12.175 水头H/m 30.07 转速n/(r·min-1) 907.4 流量q/(L·s-1) 266.1 空化数 σ 0.12(无空化)
0.04(空化)式中，pout和pv分别为水轮机出口压力和水的饱和蒸汽压，HS与H分别为水轮机的允许吸出高度和水头，ρ为水的密度，g为重力加速度。
1.2 计算设置
由于水轮机内的流动为气液两相流，数值计算中基于均质混合流假设进行处理，即将水与水蒸气的混合流体视为密度和黏度随时间与空间变化的一种均质流体。
均质流体的基本控制方程为:
∂ρ∂t+∇⋅(ρU)=0 (2) ∂(ρui)∂t+∂(ρuiuj)∂xj=−∂p∂xi+fi+∂∂xj[(μ+μt)(∂ui∂xj+∂uj∂xj)] (3) 式中，u和p分别为速度和压力，μ和μt分别为分子黏性系数和湍流黏性系数，fi为体积力。
计算中采用k-ω SST湍流模型。空化模拟中使用基于质量输运方程的Zwart空化模型[19]，其中的蒸发项与凝结项分别为式(4-5)：
˙m+=Ce3ρv(1−αv)αnucRb23max (4) {{\dot m}^ - } = {C_{\rm{c}}}\frac{{3{\rho _{\rm{v}}}{\alpha _{\rm{v}}}}}{{{R_{\rm{b}}}}}\sqrt {\frac{2}{3}\frac{{\max \left( {p - {p_{\rm{v}}}, 0} \right)}}{{{\rho _1}}}} (5) 式中，下标v和l分别代表蒸汽和水，Ce与Cc为对应蒸发与凝结过程的模型参数，按照以往经验分别取50和0.01。αnuc为液体中气核的体积分数，取5×10-4，αv为蒸汽的体积分数。
计算中，进口边界设置为总压条件，出口边界设置为静压条件(根据空化数确定)，固体边界均设置为无滑移壁面条件。计算域中，转轮以转速n旋转，对应的转频为fn= n/60=15.12 Hz，其余部分为静止部件。非定常计算的时间步长最初设置为Tn/60(Tn=1/fn，为转轮转动周期)，待计算稳定后改为Tn/120。全流道均采用结构网格，经网格无关性验证后，计算域的最终网格数为3 568 347。
2. 结果及讨论
2.1 计算结果与实验数据的对比
计算中主要采用了压力边界条件，即在计算域进口设置全压、在出口设定静压以保证计算水头、空化数与实验一致，因此，需要对比计算与实验的流量和效率，以及最为关注的压力脉动信息，以确保数值计算的可靠性。表 3为无空化工况下，数值计算与模型水轮机试验主要性能参数和压力脉动的对比。从中可以看出，流量和效率的相对误差分别为6.8%和3.6%，PA点(PA点位置如图 2所示，在未安装鳍时监测)压力脉动主要成分f1(由涡带旋转引起)的频率和无量纲幅值的相对误差分别为2.0%和5.1%。虽然数值计算与实验结果之间存在一定误差，但是考虑到计算工况为部分负荷工况，而非设计工况，因此，可以认为数值计算的结果是基本可靠的，可以用于分析尾水管中内部流动和压力脉动的特征。
表 3 数值计算与实验主要性能参数和压力脉动的对比(σ=0.12)Table 3. Comparison of turbine performance and pressure fluctuation between numerical calculation and experiment参数 实验值
(无鳍)计算值(σ= 0.12) 无鳍 相对误差/% 有鳍 流量q/(L·s-1) 266.1 284.1 6.8 283.8 效率η/% 91.05 94.37 3.6 94.54 (PA点)f1的
无量纲频率(f/fn)0.204 0.200 2.0 (PA点)f1的
无量纲幅值/%0.59 0.62 5.1 *无量纲幅值的计算公式为p/(ρgH)，H为水轮机的额定水头。 此外，从表 3中亦可以看出加鳍后，水轮机效率有轻微的上升。这是因为鳍的尺度较小，安装鳍只在一定程度上影响鳍周围的流场，而对尾水管的整体流动影响不大。而且，合适的鳍布置会提高尾水管的压力回复系数，降低总压损失[20]。在非空化工况下(σ=0.12)，加鳍使得尾水管的压力恢复系数Cpr从0.84提高到0.90。Cpr的计算式如下：
{C_{{\rm{pr}}}} = \frac{{{p_{{\rm{out}}}} - {p_{{\rm{in}}}}}}{{\frac{1}{2}\rho u_{{\rm{in}}}^2}} (6) 2.2 非空化工况尾水管压力脉动及内流场分析
为了方便讨论与分析，在尾水管中设置了若干监测点和参考面，具体位置如图 2所示。其中，监测点P1位于尾水管的入口截面上，P2、P3分别位于鳍的上端和下端，P5位于弯肘段；S1与S2为位于直锥段的横截面。
图 3为无空化工况(σ = 0.12)下尾水管中压力脉动，图中监测点1~5分别对应P1~P5。其中图 3(a)为未安装鳍时的压力脉动频域特性，而图 3(b)为安装鳍后的情况。
![]()
图 3 各监测点处的压力脉动频谱图(σ=0.12)Figure 3. The pressure fluctuation spectrum at each monitor point (σ=0.12)从图 3(a)所示的压力脉动频谱图中可以看出，尾水管未安装鳍时流场中主要存在两个成分的压力脉动，分别记为f1与f2。由表 4可知，主要压力脉动成分f1与f2的相对频率(f/fn)分别为0.20和0.13，其中压力脉动成分f1是涡带所诱导的。需要说明的是，在模型水轮机试验中同样出现了频率为0.13 fn的压力脉动成分。研究表面，该成分是尾水管弯肘段结构与涡带之间的相互作用所致。在直锥段(即P1~P4)，压力脉动的主要成分均为f1，即主频为0.20 fn，压力脉动的最大幅值出现在P3点附近；而在弯肘段，压力脉动成分f2的幅值超过f1，0.13 fn成为主频。
如图 3(b)所示，在尾水管中加鳍后，压力脉动成分f2基本消失，而f1成为整个尾水管中的主要压力脉动成分。在直锥段P1~P4，压力脉动成分 f1的幅值均有一定幅度的降低。这证明了尾水管壁面加鳍有利于抑制水轮机部分负荷工况下的压力脉动；而在弯肘段P5处，f1的幅值反而出现了较为明显的上升。
表 4列举了无空化工况下尾水管中压力脉动主要成分的频率和幅值。
表 4 尾水管中压力脉动主要成分的频率和幅值(σ=0.12)Table 4. The frequency and amplitude of main pressure fluctuation components in the draft tube (σ=0.12)监测点 P1 P2 P3 P4 P5 无鳍 f1 相对频率
(f/fn)0.201 0.200 0.200 0.200 0.198 无量纲
幅值/%0.614 0.606 0.644 0.502 0.233 f2 相对频率
(f/fn)0.132 0.132 0.134 0.135 0.134 无量纲
幅值/%0.304 0.305 0.228 0.221 0.481 加鳍 f1 相对频率
(f/fn)0.202 0.202 0.202 0.201 0.202 无量纲
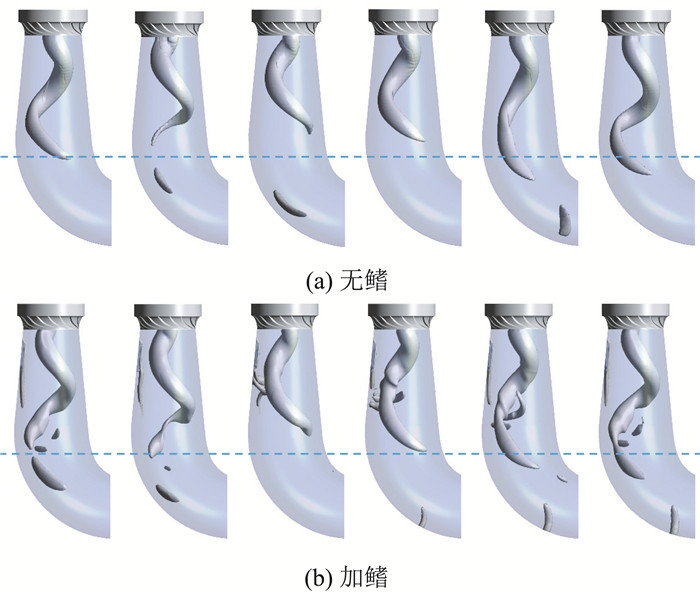
幅值/%0.510 0.476 0.566 0.432 0.486 在低负荷工况下尾水管的压力脉动与涡带运动紧密相关，要分析加鳍影响压力脉动的机制，就需要对内部的涡带运动进行详细考察。图 4表示基于Q准则的涡带随时间演化。如图 4(b)所示，加鳍后，流场中除了已有的主流区涡带(主流区涡带运动是f1成分的成因)，在鳍附近出现了另一条额外的小涡带，这是由于鳍对旋流的阻碍而产生的。小涡带对鳍附近的近壁区流动控制强于主流区涡带的影响，因此小涡带对鳍附近的压力影响更强。而由于小涡带的周期性运动远弱于主流区涡带，鳍附近的压力变动显然也会比未加鳍时减弱，即加鳍降低了鳍附近压力脉动的幅值。
![]()
图 4 尾水管中涡带的运动(Q=1500 s-1, σ=0.12)Figure 4. The vortex rope motion in the draft tube (Q=1500 s-1, σ=0.12)但同时注意到，主流区涡带每旋转一周，都会与小涡带发生一次交互作用，该作用强化了压力脉动中的f1成分，同时对小涡带产生挤压、扯断、裹挟等作用，使得鳍下游的涡带碎片增多，恶化了直锥段下游以及弯肘段的流动，使得P5处的压力脉动升高。此外，应当注意到，加鳍对主流区涡带的规模(如涡带长度)并无明显影响，其主要作用体现在附鳍小涡带使得主流区涡带的末端发生断裂，使得弯肘段的涡带碎片增多。
图 5为P3点所在尾水管横截面上涡带旋转一周的涡心轨迹示意图。其中涡心由横截面上压力最低点表示，距离涡心越远，压力越高。在涡带的旋转过程中，随着涡带的靠近和远离，监测点处的压力也对应地下降和上升。因此，不难理解，涡心轨迹的直径越大，监测点的压力脉动也越剧烈。从图 5中可以看出，鳍使得涡心轨迹向远离鳍的一侧移动，并略微减小了涡心轨迹的直径，使得压力脉动幅值降低。
![]()
图 5 P3所在横截面上涡心轨迹示意图(σ=0.12)Figure 5. The trajectory of vortex core on the section where P3 locates (σ=0.12)图 6对比了无鳍和加鳍两种情况下，两个时间瞬间S1和S2截面上的压力分布。从中亦可以看出，小涡带产生的低压区影响了鳍周围的压力分布，在主流区涡带旋转的过程中，起到稳定流动的作用，一定程度上降低了涡带诱发的压力脉动。
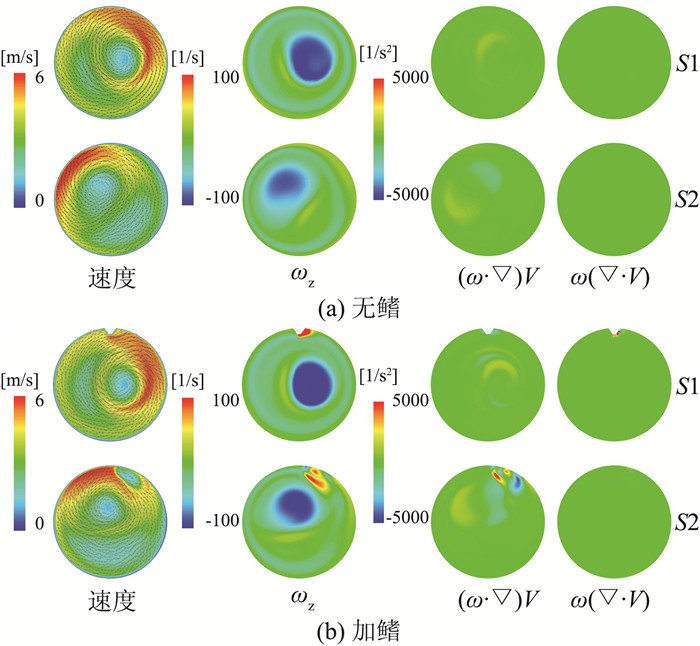
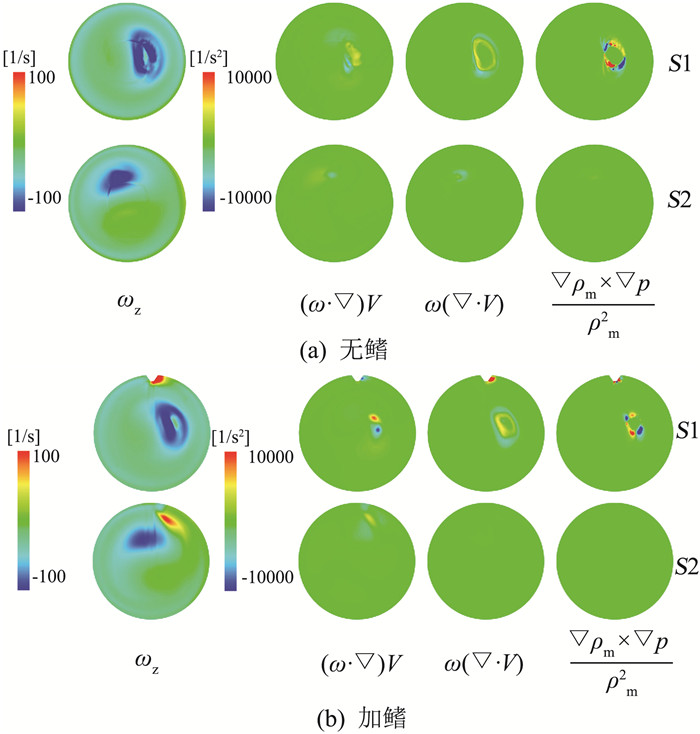
尾水管中涡带的形成与尾水管入口的旋流密不可分，其运动更与尾水管中涡的演变息息相关，尤其是Z方向涡量ωz在尾水管中的变化和发展。因此，为了更清楚地理解鳍对涡带的作用，以及对压力脉动的影响，本文使用式(7)所示的涡输运方程对尾水管中的涡输运情况进行了分析。
\frac{{D\omega }}{{Dt}} = (\omega \cdot \nabla )V - \omega (\nabla \cdot V) + \frac{{\nabla {\rho _{\rm{m}}} \times \nabla p}}{{\rho _{\rm{m}}^2}} + \nu \left( {{\nabla ^2}\omega } \right) (7) 式中，ω为涡量。涡输运方程左边为涡量变化率，右边四项依次为拉伸项、膨胀项、斜压扭矩项和黏性项。由文献[17]可知，黏性项相比于其余三项很小，可以忽略不计。而在非空化工况下，流体的密度不变，因而斜压扭矩项为零。因此，对涡量变化率起主要作用的是涡的拉伸项和膨胀项。图 7展示了t0+2T/5时刻S1和S2截面上的速度、涡量ωz、拉伸项和膨胀项的分布。
![]()
图 7 t0+2T/5时刻S1和S2截面上的速度、涡量ωz、拉伸项和膨胀项的分布(σ=0.12)Figure 7. Distributions of the velocity, vorticity, stretching term and expansion term on S1 and S2 at the instant of t0+2T/5(σ = 0.12)从图 7中可以看出，无鳍工况下，涡的拉伸项是造成涡量变化的主要因素，该项由流场中的高速度梯度所引起。拉伸项主要存在于主流区，且存在一正一负两个高值区，分布在涡量高值区的边缘。拉伸项一正一负成对存在，使得涡量高值区的涡量一侧降低，一侧增加，表现为涡量高值区的圆周运动，即涡带的旋转。加鳍以后，主流区未受明显影响，拉伸项仍是主要作用因素。鳍的作用主要集中在鳍附近。从速度分布中可以看出鳍对流动的阻碍作用，使得鳍附近产生了巨大的速度梯度，此处涡的拉伸项比主流区更加明显，膨胀项的作用也达到了和拉伸项相近的量级。在S1截面，鳍附近的高膨胀项诱发了附鳍小涡带的产生；而S2截面上成对出现的拉伸项高值区，是主流区涡带和附鳍小涡带相互作用的结果。
2.3 空化工况尾水管压力脉动及内流分析
在空化工况(σ=0.04)下，f1成分(及其谐频)成为尾水管中压力脉动的唯一主频，但幅值相对于无空化工况亦有较大程度的上升。从图 8及表 5中可以看出，尾水管中空化的产生消除了压力脉动中除主频之外的其他频率成分。在尾水管内不同监测点处，鳍的作用均表现为降低压力脉动幅值，效果相对于无空化工况时更为明显。
![]()
图 8 各监测点的压力脉动频谱图(σ=0.04)Figure 8. The pressure fluctuation spectrum at each monitor point (σ=0.04)表 5 尾水管中压力脉动主要成分的频率和幅值(σ=0.04)Table 5. The frequency and amplitude of main pressure fluctuation components in the draft tube (σ=0.04)监测点 P1 P2 P3 P4 P5 无鳍 f1 相对频率
(f/fn)0.212 0.212 0.212 0.212 0.212 无量纲
幅值/%0.841 0.906 1.209 0.792 0.480 加鳍 f1 相对频率
(f/fn)0.214 0.215 0.214 0.214 0.214 无量纲
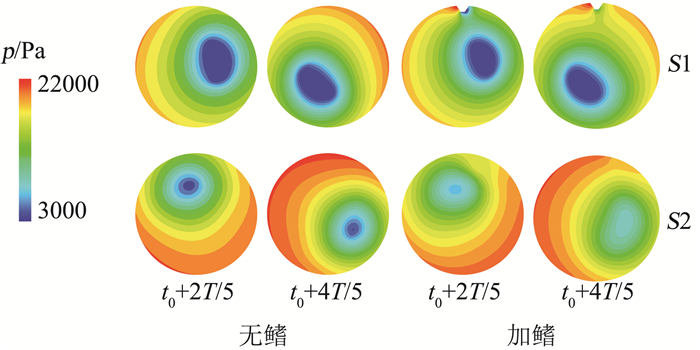
幅值/%0.563 0.507 0.749 0.599 0.307 未安装鳍时，从图 9(a)所示的尾水管中压力脉动和空泡体积变化曲线中不难看出，空泡体积脉动与压力脉动基本上同频率同相位，二者的“共振”作用强化了压力脉动，使得f1成分的幅值出现了较大幅度的提高；而图 10(b)亦反映出空泡的出现显著增大了涡带规模。二者的共同作用使得空化工况下的压力脉动，尤其是f1成分的幅值显著增大。
![]()
图 10 不同工况下尾水管中涡带和空泡(蓝色：空泡；灰色：涡带)Figure 10. Vortex rope and cavity in the draft tube under different working conditions (blue: the vortex rope; gray: air)如图 9(b)所示，加鳍以后尾水管中空泡的体积和脉动幅值显著减小，涡带规模明显得到削弱(如图 10(c))，尾水管各截面上最低压力升高，压力梯度降低，鳍的稳压作用依旧明显(如图 11)。在这些因素综合作用下，尾水管中压力脉动幅值显著降低。
图 12为空化工况下P3所在横截面上的涡心轨迹示意图。与非空化工况类似，鳍的存在使得涡心轨迹向远离鳍的一侧移动，涡心轨迹的直径也有所减小，且相对于非空化工况，减小幅度更大，充分说明了加鳍抑制涡带运动及其诱导压力脉动的作用更为明显。
![]()
图 12 P3所在横截面上涡心轨迹示意图(σ= 0.04)Figure 12. The trajectory of vortex core on the section where P3 locates (σ=0.04)从涡输运的角度分析，空化工况与非空化工况下鳍作用的区别主要体现在鳍对空泡的影响。由图 13可以看出，膨胀项和斜压扭矩项的作用最为突出，且二者均分布在空泡的表面。膨胀项呈环状分布，且存在内外一正一负两个环，代表着其对空泡体积的作用，使得空泡体积随时间而变化。斜压扭矩项分布也呈环状，但其正负交错出现，意味着其将使得涡绕尾水管中心进动的同时，也将绕涡核中心旋转。拉伸项的分布类似于非空化工况，其作用将使涡绕尾水管中心进动，即促进了压力脉动成分f1的增强。
![]()
图 13 S1和S2截面上的涡量ωz、拉伸项、膨胀项和斜压扭矩项的分布(σ=0.04)Figure 13. Distributions of the vorticity, stretching term, expansion term and baroclinic term on S1 and S2 (σ = 0.04)而在鳍的下游，空泡已经消失，所以在S2截面上拉伸项和膨胀项的分布和作用与非空化工况下基本接近。
3. 结论
本文研究结果表明尾水管壁面加鳍对空化状态下尾水管涡带及其诱导压力脉动有显著的抑制作用。作为一种被动控制方法，壁面加鳍简单易行，且对水轮机整体性能无明显影响，可作为工程中抑制尾水管压力脉动的可行策略之一。具体结论如下：
1) 鳍表面出现的附鳍小涡带能够起到稳定鳍附近压力场的作用，缓解了尾水管直锥段的压力脉动；附鳍小涡带与主流区涡带的相互作用则恶化了非空化工况下鳍下游的流动，使得弯肘段的压力脉动有一定幅度的回升。
2) 空化工况下空泡体积脉动与压力脉动同频率同相位，使得尾水管内压力脉动幅值显著增大。加鳍抑制了空化涡带的生长，降低了空泡体积，从而缓解了空化工况下的压力脉动。
3) 鳍影响尾水管流场中的速度、压力分布和空泡体积，并通过涡输运方程中的拉伸项、膨胀项和斜压扭矩项影响涡带的发展，进而影响压力脉动。
致谢: 本文的数值计算获得清华信息科学与技术国家实验室支持。 -
![]()
图 3 各监测点处的压力脉动频谱图(σ=0.12)
Figure 3. The pressure fluctuation spectrum at each monitor point (σ=0.12)
![]()
图 4 尾水管中涡带的运动(Q=1500 s-1, σ=0.12)
Figure 4. The vortex rope motion in the draft tube (Q=1500 s-1, σ=0.12)
![]()
图 5 P3所在横截面上涡心轨迹示意图(σ=0.12)
Figure 5. The trajectory of vortex core on the section where P3 locates (σ=0.12)
![]()
图 7 t0+2T/5时刻S1和S2截面上的速度、涡量ωz、拉伸项和膨胀项的分布(σ=0.12)
Figure 7. Distributions of the velocity, vorticity, stretching term and expansion term on S1 and S2 at the instant of t0+2T/5(σ = 0.12)
![]()
图 8 各监测点的压力脉动频谱图(σ=0.04)
Figure 8. The pressure fluctuation spectrum at each monitor point (σ=0.04)
![]()
图 10 不同工况下尾水管中涡带和空泡(蓝色：空泡；灰色：涡带)
Figure 10. Vortex rope and cavity in the draft tube under different working conditions (blue: the vortex rope; gray: air)
![]()
图 12 P3所在横截面上涡心轨迹示意图(σ= 0.04)
Figure 12. The trajectory of vortex core on the section where P3 locates (σ=0.04)
![]()
图 13 S1和S2截面上的涡量ωz、拉伸项、膨胀项和斜压扭矩项的分布(σ=0.04)
Figure 13. Distributions of the vorticity, stretching term, expansion term and baroclinic term on S1 and S2 (σ = 0.04)
表 1 水轮机几何参数
Table 1 Geometric parameters of the Francis turbine
参数 数值 转轮进口直径Dr/mm 420 转轮叶片数Zb 17 活动导叶数 24 固定导叶数 23 导叶相对高度b0=b/Dr 0.183 
下载: 导出CSV
表 2 水轮机运行参数
Table 2 Operating parameters of the Francis turbine
参数 数值 活动导叶开度α0/mm 12.175 水头H/m 30.07 转速n/(r·min-1) 907.4 流量q/(L·s-1) 266.1 空化数 σ 0.12(无空化)
0.04(空化)
下载: 导出CSV
表 3 数值计算与实验主要性能参数和压力脉动的对比(σ=0.12)
Table 3 Comparison of turbine performance and pressure fluctuation between numerical calculation and experiment
参数 实验值
(无鳍)计算值(σ= 0.12) 无鳍 相对误差/% 有鳍 流量q/(L·s-1) 266.1 284.1 6.8 283.8 效率η/% 91.05 94.37 3.6 94.54 (PA点)f1的
无量纲频率(f/fn)0.204 0.200 2.0 (PA点)f1的
无量纲幅值/%0.59 0.62 5.1 *无量纲幅值的计算公式为p/(ρgH)，H为水轮机的额定水头。
下载: 导出CSV
表 4 尾水管中压力脉动主要成分的频率和幅值(σ=0.12)
Table 4 The frequency and amplitude of main pressure fluctuation components in the draft tube (σ=0.12)
监测点 P1 P2 P3 P4 P5 无鳍 f1 相对频率
(f/fn)0.201 0.200 0.200 0.200 0.198 无量纲
幅值/%0.614 0.606 0.644 0.502 0.233 f2 相对频率
(f/fn)0.132 0.132 0.134 0.135 0.134 无量纲
幅值/%0.304 0.305 0.228 0.221 0.481 加鳍 f1 相对频率
(f/fn)0.202 0.202 0.202 0.201 0.202 无量纲
幅值/%0.510 0.476 0.566 0.432 0.486
下载: 导出CSV
表 5 尾水管中压力脉动主要成分的频率和幅值(σ=0.04)
Table 5 The frequency and amplitude of main pressure fluctuation components in the draft tube (σ=0.04)
监测点 P1 P2 P3 P4 P5 无鳍 f1 相对频率
(f/fn)0.212 0.212 0.212 0.212 0.212 无量纲
幅值/%0.841 0.906 1.209 0.792 0.480 加鳍 f1 相对频率
(f/fn)0.214 0.215 0.214 0.214 0.214 无量纲
幅值/%0.563 0.507 0.749 0.599 0.307
下载: 导出CSV
-
[1] JACOB T. Pressure fluctuations of francis turbines: model and prototype test results[C]//Modeling, Testing and Monitoring for hydropower plants-Ⅱ, Lausanne, Switzerland, 1996.
[2] JACOB T, PRÉNAT J E. Francis turbine surge: discussion and data base[C]//Proceedings of 18th IAHR Symposium, Valencia. Spain, 1996.
[3] 罗先武.通气工况下混流式水轮机尾水管压力脉动特性分析[C]//第十四届全国水动力学学术会议暨第二十八届全国水动力学研讨会文集(上册).上海: 《水动力学研究与进展》杂志社, 2017: 649-664. LUO X W. Pressure fluctuation analysis for Francis turbine draft tube with air admission[C]//14th national symposium on hydrodynamics i.e. 28th national symposium on hydrodynamics (part Ⅰ). Shanghai: Journal of Hydrodynamics, 2017: 649-664. (in Chinese)
[4] RHEINGANS W J. Power swings in hydroelectric power plants[J]. Transactions of the ASME, 1940, 62:171-184. https://www.usgs.gov/special-topic/water-science-school/science/hydroelectric-power-water-use
[5] CASSIDY J J, FALVEY H T. Frequency and amplitude of pressure surges generated by swirling flows[C]//IAHR Section Hydraulic Machinery, Equipment, and Cavitation, 5th Symposium, 1970, Stockholm, Sweden.
[6] 徐洪泉, 孟晓超, 张海平, 等.空腔危害水力机械稳定性理论Ⅲ——空腔对尾水管涡带压力脉动的影响和作用[J].水力发电学报, 2013, 32(04):204-208. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=slfdxb201304036 XU H Q, MENG X C, ZHANG H P, et al. Theory of cavitation bubbles conglomeration endangering stability of hydraulic machinery Ⅲ:effects on pressure fluctuations of vortex rope coming from cavitation bubbles conglomeration in draft tube[J]. Journal of Hydroelectric Engineering, 2013, 32(4):204-208. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=slfdxb201304036
[7] DÖRFLER P, SICK M, COUTU A. Flow-induced pulsation and vibration in hydroelectric machinery[M]. London:Springer-Verlag, 2013.
[8] ARPE J, NICOLET C, AVELLAN F. Experimental evidence of hydroacoustic pressure waves in a francis turbine elbow draft tube for low discharge conditions[J]. ASME Journal of Fluids Engineering, 2009, 131(8):0811021-1-9. https://core.ac.uk/display/12623672
[9] YAMAMOTO M, MVLLER A, FAVREL A, et al. Pressure measurements and high speed visualizations of the cavitation phenomena at deep part load condition in a Francis turbine[C]//27th IAHR Symposium on Hydraulic Machinery and Systems, IOP Conf. Series: Earth and Environmental Science, 2014, 22: 022011.
[10] 周凌九, 王正伟.基于空化流动计算的混流式水轮机尾水管的压力脉动[J].清华大学学报(自然科学版), 2008(06):972-976. doi: 10.3321/j.issn:1000-0054.2008.06.016 ZHOU L J, WANG Z W. Pressure Fluctuations in a francis turbine draft tube calculated by cavitating flow simulation[J]. Journal of Tsinghua University (Science and Technology), 2008, 48(6):972-976. (in Chinese) doi: 10.3321/j.issn:1000-0054.2008.06.016
[11] NISHI M, WANG X M, YOSHIDA K, et al. An experimental study on fins, their role in control of the draft tube surging[J]. Hydraulic Machinery and Cavitation, 1996:905-914. doi: 10.1007%2F978-94-010-9385-9_92
[12] NISHI M, KAWAI K, YOSHIDA K, et al. Installation of a fin as a means to alleviate the draft tube surging[C]//Proc Third ASME/JSME Joint Fluids Engineering Conf, San Francisco, 1999: 99-7209.
[13] DMITRY P, ANDREY, M, DMITRY D. The study of the influence of stabilizing devices on the pressure pulsations at the free discharge of water through the turbine[C]//MATEC Web of Conferences, 2017, 115: 06002.
[14] NAKANISHI K, UEDA T. Air Supply into Draft Tube of Francis Turbine[J]. Fuji Electric Review, 1964, 10:81-91.
[15] QIAN Z D, YANG J, HUAI W. Numerical simulation and analysis of pressure pulsation in francis hydraulic turbine with air admission[J]. Journal of Hydrodynamics, Ser B, 2007, 19(4):467-472. doi: 10.1016/S1001-6058(07)60141-3
[16] LIAO W L, JI J T, LU P, et al. Effect of air admission through center hole of turbine shaft on the flow in draft tube[J]. Journal of Hydraulic Engineering, 2008, 39(8):1005-1011. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=slxb200808018
[17] 于安.补气对水轮机尾水管压力脉动及涡流特性的影响分析[D].清华大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10003-1018875920.htm YU A. Analysis of the pressure fluctuations and vortical flow characteristics in a francis turbine draft tube with air admission[D]. Tsinghua University, 2017. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10003-1018875920.htm
[18] NISHI M, YOSHIDA K, FUJII M, et al. A study on hybrid control of draft tube surge[C]//Proceedings of the XXIst IAHR Symposium on Hydraulic Machinery and Systems, Lausanne Switzerland, 2002.
[19] ZWART P J, GERBER A G, BELAMRI T. A two-phase flow model for predicting cavitation dynamics[C]//Fifth International Conference on Multiphase Flow, Yokohama, Japan, 2004.
[20] 马震岳, 陈婧, 西道弘.设置消减压力脉动稳流片后尾水管数值解析[J].大连理工大学学报, 2003, 43(02):181-186. doi: 10.3321/j.issn:1000-8608.2003.02.013 MA Z Y, CHEN J, NISHI M. Numerical research on fins to alleviate draft tube surging[J]. Journal of Dalian University of Technology, 2003, 43(2):181-186. (in Chinese) doi: 10.3321/j.issn:1000-8608.2003.02.013
-
期刊类型引用(7)
1. 冯赵展，于凤荣，徐瑞红. 混流式水轮机内部流场模拟分析. 中国水运(下半月). 2022(02): 48-50 . 
百度学术
2. 罗先武，叶维祥，宋雪漪，耿晨. 支撑“双碳”目标的未来流体机械技术. 清华大学学报(自然科学版). 2022(04): 678-692 . 百度学术
3. 冯赵展，于凤荣，罗竹梅，邹屹东，聂聪，杨怀荣，耿贞伟. 混流式水轮机尾水管流场数学模型建立及分析. 水力发电. 2022(10): 77-81+112 . 百度学术
4. 孙文，李建兵，宋慧涛. 白鹤滩水电站左岸尾水管安装施工方案研究. 四川建材. 2022(12): 180-181 . 百度学术
5. 靳海宁，杨孝作，王前，司马俊杰. 关于三峡通航智能调度系统建设的思考. 中国水运. 2022(04): 59-60 . 百度学术
6. 朱国俊，陈旻甲，冯建军，刘可然，罗兴锜. 基于样本熵的高水头混流式水轮机稳定性分析. 农业机械学报. 2021(07): 134-140+101 . 百度学术
7. 马越，钱冰，冯治国，刘小兵，王彬鑫. 横梁孔对轴流式水轮机尾水管内流特性的影响. 人民黄河. 2021(S2): 122-124 . 百度学术
其他类型引用(3)
计量
- 文章访问数: 236
- HTML全文浏览量: 60
- PDF下载量: 90
- 被引次数: 10
