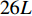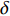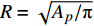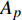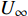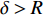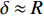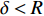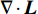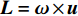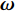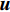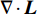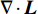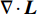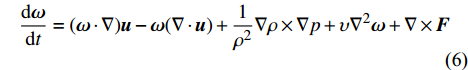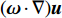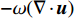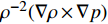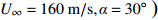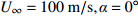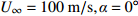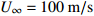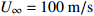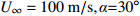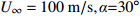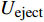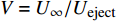The inflation process and safety analyses of a parachute ejected from civil aircrafts
-
摘要: 当降落伞牵引小质量负荷（应急数据记录系统）从大型民用飞机机身下方弹射离机时，不同于弹体等刚性物体，柔性伞衣充气过程中剐蹭机身等安全隐患更大。为了研究弹射降落伞离机充气过程气动特性和运动轨迹，采用任意拉格朗日-欧拉（arbitrary Lagrange Euler, ALE）方法，对不同来流速度和角度条件下的降落伞开伞过程、气动特性和流场特性进行了数值模拟，分析了来流速度和角度对伞衣充气过程的影响。结果表明：当伞衣贴近或挤压机身时，伞衣侧面剪切层和近尾迹区中的涡运动都会受到机身影响，但降落伞不会完全失效，这时伞衣投影面积相对较小，充气过程的动载峰值变小。同时，在 40～160 m/s来流速度、临界来流迎角下，给出了降落伞可安全弹射离机的来流条件，为分离式飞机应急记录跟踪系统设计提供了理论支持。Abstract: The ejectable emergency flight data recorder equipped with a parachute show promising prospects in aircraft safety and rescue. However, compared to rigid objects, the flexible canopy of an ejected parachute during its inflation process is more likely to collide with the fuselage, which brings potential safety hazards. Therefore, the aerodynamic characteristics and trajectories of a parachute ejected from a civil aircraft are studied numerically by the Arbitrary Lagrange Euler method (ALE). The effects of the free-stream conditions, i.e., the velocity and angle of attack on the parachute inflation process, aerodynamic characteristics, and flow fields are analyzed. Results show that when the parachute is close to the fuselage, the shear layers and vortical motions around the canopy are modified by the fuselage. Nevertheless, the parachute does not fail completely. Meanwhile, the projected area and opening load of the canopy are relatively small. The critical angle of attack of at the free-stream with velocity bewteen 40 m/s and 160 m/s is obtained. The safety condition for ejections is given at last. This work provides a theoretical support for the design of ejectable flight data recording and emergency tracking systems.
-
0. 引 言
传统飞行数据记录器（flight data recorder, FDR）都是固定在机身中。如果客机在跨洋飞行中发生空难，FDR会随飞机残骸沉入海底。马航370航班失联后，南京航空航天大学民机救生团队与中国商飞针对民航客机联合研发了分离式应急记录跟踪系统，该系统又被称为报信者（Harbinger, HBG）系统[1-4]。系统中装备了可快速弹射的小型降落伞，可以依靠气动力在飞机处于紧急状态时将应急飞行数据记录器（emergency flight data recorder, EFDR）拉出飞机。随后利用降落伞和气囊气动阻力，降低EFDR的坠落速度，减小坠落冲击。如果降落伞在充气过程中剐蹭机身，则可能导致伞衣破损，气囊漏气，引起气囊降落伞失效，设备损坏。研究不同工况下的降落伞充气过程，分析伞的运动轨迹，判断其工作过程中的安全性对设计理论和工程应用都有重要意义。
在空降空投领域，研究手段主要是空投试验、风洞试验和数值模拟。但在涉及降落伞的离机过程时，空投试验不仅费用昂贵，且载机还有一定安全风险，所以在设计研究阶段往往以风洞试验和数值模拟为主。
在人员离机过程的研究中，刘洋等[5]利用风洞试验研究了民航飞机试飞员应急离机的运动轨迹，分析了离机方案的安全性。刘晓宇等[6]通过动态嵌套网格技术模拟了人员跳伞离机的过程。在运输机空投货物的研究中，Bergmann等[7]针对降落伞的离机过程进行了风洞试验，试验中将降落伞简化为刚性半球壳，测量了降落伞的运动轨迹。Schade等[8]采用嵌套网格技术模拟了试验[7]中的空投过程，但发现过程中降落伞离机的初始阶段误差较小，随后误差逐渐增大，运动轨迹和俯仰角的最大误差约为18%。Roosenboom等[9]进一步完善了空投过程的风洞实验，试验中同样采用了刚性降落伞模型，应用PIV技术测量了飞机尾流场。Geisbauer等[10]对比了数值模拟与试验[9]中的流场结构，验证了数值模拟方法的可靠性。为了研究飞机尾流对降落伞气动力的影响，Tezduyar等[11]采用多计算域（multi-domain method, MDM）方法，分别将飞机和降落伞放置于不同的计算域内，模拟了柔性降落伞在飞机远尾流区中的运动。Serrano等[12]将刚性牵引伞固定在运输机近尾流区中，采用数值模拟方法分析了运输机尾流对牵引伞气动力的影响。除此以外，近年来美国陆军纳蒂克士兵研发与工程中心（NSRDEC）和美国空军学院高性能计算中心合作[13-14]，采用大规模数值模拟的方法（最大网格数约为2亿），研究了空投空降过程中飞机附近的流场结构，并分析了飞机尾流对伞兵、货物和牵引伞气动特性的影响。其中Bergeron等[14]将刚性牵引伞模型固定在C17运输机尾部舱门后方，分析了牵引伞前方来流的特点，研究了运输机尾流对牵引伞的气动力影响。
可以看到，研究中往往将人员、货物和降落伞等简化为刚性物体。虽然刚性物体从机身离机研究较多，但柔性、随机、小质量载荷、大变形的降落伞在民机弹射离机研究还不多见。本文针对从机身下方弹射离机的降落伞充气过程进行了数值研究，分别模拟了有/无机身影响下的伞衣充气过程，分析了伞衣剪切层和近尾迹区的流场特征，以及机身和来流角度对伞衣充气过程的影响，给出了降落伞安全离机的临界迎角。
1. 数值计算方法与验证算例
针对伞衣充气过程中的柔性体大变形流固耦合问题，采用ALE方法进行数值模拟。HBG系统降落伞最大开伞速度为160 m/s，马赫数约为0.46，可压缩流体控制方程为：
\frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {{\boldsymbol{x}}_i}}}(\rho {{\boldsymbol{u}}_i}) = 0 (1) \begin{split}& \frac{{\partial {{\boldsymbol{u}}_i}}}{{\partial t}} + {{\boldsymbol{u}}_j}\frac{{\partial {{\boldsymbol{u}}_i}}}{{\partial {{\boldsymbol{x}}_j}}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {{\boldsymbol{x}}_i}}} + \frac{1}{\rho }\frac{\partial }{{\partial {{\boldsymbol{x}}_i}}}\left( {\lambda \frac{{\partial {{\boldsymbol{u}}_k}}}{{\partial {{\boldsymbol{x}}_k}}}} \right) +\\&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \frac{1}{\rho }\frac{\partial }{{\partial {{\boldsymbol{x}}_j}}}\left[ {\mu \left( {\frac{{\partial {{\boldsymbol{u}}_j}}}{{\partial {{\boldsymbol{x}}_j}}} + \frac{{\partial {{\boldsymbol{u}}_j}}}{{\partial {{\boldsymbol{x}}_i}}}} \right)} \right] + {{\boldsymbol{f}}_i} \end{split} (2) \begin{array}{l} \dfrac{{\partial \varepsilon }}{{\partial t}} + {{\boldsymbol{u}}_i}\dfrac{{\partial \varepsilon }}{{\partial {{\boldsymbol{x}}_i}}} = - \dfrac{p}{\rho }\left( {\dfrac{{\partial {{\boldsymbol{u}}_i}}}{{\partial {{\boldsymbol{x}}_i}}}} \right) + \dfrac{1}{\rho }\varPhi {\rm{ }} + \dfrac{1}{\rho }\dfrac{\partial }{{\partial {{\boldsymbol{x}}_i}}}\left( {k\dfrac{{\partial T}}{{\partial {{\boldsymbol{x}}_i}}}} \right) \end{array} (3) 其中，
t 为时间，\;\rho 为流体密度，{{\boldsymbol{u}}_i} 为流体速度张量，p 为流体压力，{f_i} 为体积力张量，\varepsilon 为流体比内能，\varPhi 为耗散函数，T 为流体温度。由于ALE方法在欧拉和拉格朗日坐标之外引入了参考坐标，所以在ALE方法中，材料域的节点信息需要被映射到空间域内，其流场变量的输运方程为：
\frac{{\partial \phi }}{{\partial t}} + \left( {{{\boldsymbol{u}}_i} -{\boldsymbol{ u}}_i^g} \right)\frac{{\partial \phi }}{{\partial {{\boldsymbol{x}}_i}}} = 0 (4) \phi \left( {{{\boldsymbol{x}}_i},0} \right) = {\phi _0}\left( {x} \right) (5) 其中，
\phi 为流场变量，{\phi _0} 为当前时间步流场变量的初始值，{\boldsymbol{u}}_i^g 为材料速度张量，当{\boldsymbol{u}}_i^g{\rm{ = }}0 时对应欧拉方法，当{\boldsymbol{u}}_i^g{\rm{ = }}{{\boldsymbol{u}}_i} 时对应拉格朗日方法。本文采用罚函数方法进行流固耦合计算。罚函数算法会时刻监控流体与结构体之间是否发生穿透，如果流体与结构体没有发生穿透，则流固耦合力为零；如果流体与结构体发生穿透，则同时对流体和结构体施加大小相同方向相反的耦合力。
为了验证降落伞展开过程，采用Heinrich等[15]的风洞试验对数值模拟方法进行验证。试验中采用了C9伞的缩比模型，伞衣名义直径
{D_0} 为0.914 m，前置体重0.251 kg，来流速度15.3 m/s。降落伞折叠模型如图1所示，计算域尺寸为6{D_0} \times 6{D_0} \times 9{D_0} 。在风洞试验中，前置体悬挂于风洞外部，通过滑轮绳索系统与降落伞相连，无前置体尾流影响。因此，数值模拟中前置体简化为质点。图2给出了当前计算的开伞动载gn与三次试验数据的对比。可以看出，在充气初始阶段，计算和试验数据趋势一致但有差异，主要缘于随机性影响[16]。在充气过程后期，伞衣接近充满状态，这时随机因素的影响会明显减弱，计算结果和试验数据吻合更好。
![]()
图 2 试验和数值模拟中的开伞动载Figure 2. The parachute opening loads in experiments and numerical simulation2. 计算模型
机身和降落伞模型如图3所示，伞型为平面圆形伞，伞衣名义直径为1.9 m。坐标系x轴为流向，y轴为展向，z为横向。离机后降落伞位于机身下方贴近蒙皮的位置，伞衣初始状态如图1所示。因为在开伞过程中前置体体积较小，所以将前置体简化为一个质点，质量为4 kg。计算域采用O形网格（图4），计算域直径为
26L ，其中L为机身长度，在伞衣充气区域进行局部加密，总网格数约为5.4×106，为保证质量守恒，计算域边界采用速度入口。根据美国国家运输安全委员会（National Transportation Safety Board, NTSB）在1990年～2020年的事故报告，取有人员死亡的大型客机空难案例进行分析。在83%的案例中，飞机坠毁前的空速处于40～160 m/s的区间。模拟工况来流速度分别为40、70、100、130、160 m/s。初始时刻，降落伞弹射离机速度10 m/s，方向为z轴负方向，本文所述迎角均为飞机来流迎角。
3. 结果和分析
3.1 流场分析
为方便分析，定义在开伞动载峰值时刻伞衣底边中心点A沿降落伞径向与飞机机身的距离为
\delta ，以及伞衣底边投影半径R = \sqrt {{{{A_p}} / {\text{π}} }} ，其中{A_p} 为伞衣底边投影面积，如图5所示。为获得迎角的影响，分析了来流速度100 m/s，来流迎角分别为0°～30°的5种工况。同样，为研究来流速度影响，分析了迎角30°，来流速度{U_{\infty} } 的5种工况，如图6所示。结果表明，伞衣与机身的距离随着来流迎角和速度的上升而下降。根据伞衣与机身的相对位置，伞衣充气过程可以被分为3中典型状态：当\delta > R 时，伞衣远离；当\delta \approx R 时，伞衣贴近机身；当\delta < R 时，伞衣与机身发生挤压剐蹭。![]()
图 5 降落伞与机身尾部相对位置示意图Figure 5. Schematic diagram of the relative position between a parachute and a fuselage tail![]()
图 6 动载峰值时刻伞衣与机身的距离Figure 6. The distance between a parachute and a fuselage when the opening load reaches its maximum以往研究表明，伞衣外形变化过程与剪切层的演化密切相关[17]。图7给出了来流速度160 m/s、迎角30°、来流速度100 m/s、迎角30°和来流速度100 m/s、迎角0°这3种工况计算结果。图7（a～c）为不考虑机身影响的工况，如图所示，伞衣底边分离点后形成了相对稳定的剪切层。而机身影响会改变流场特性，如图7（d～f）：当伞衣贴近机身或与机身发生挤压时（图7（d、e）），伞衣靠近机身位置处剪切层消失，伞衣近尾流区的压力没有出现急剧下降；当伞衣与机身距离较远时（图7（f）），伞衣靠近机身一侧又出现了剪切层结构，机身影响变得不明显。
![]()
图 7 动载峰值时刻伞衣对称面的压力云图，等值线为流向速度Figure 7. Flow fields at the parachute symmetrical plane (Shade and line contours denote pressure and streamwise velocity, respectively)Lamb矢量散度与流场中的动量输运过程相关，可被用于研究流场演化的动力学过程[18]。Lamb矢量散度定义为
\nabla \cdot {\boldsymbol{L}} 。这里，{\boldsymbol{L}} = {\boldsymbol{\omega}} \times {\boldsymbol{u}} 为Lamb矢量；{\boldsymbol{\omega}} 为伪涡矢量；{\boldsymbol{u}} 为流体速度矢量。因为伞衣充气过程主要受剪切层和涡结构运动影响，故\nabla \cdot {\boldsymbol{L}} 可被用于描述伞衣附近流场特征[19]。图8给出了利用Lamb矢量散度描述的流场拓扑结构，其中图8（a～c）为不考虑机身影响的工况。可以看出，在自由来流中，剪切层在伞衣底边分离后，
\nabla \cdot {\boldsymbol{L}} 产生了负值包裹正值的三层结构，类似结构可以减缓剪切层失稳[20]。在伞衣的近尾迹区中，\nabla \cdot {\boldsymbol{L}} 演化为正负交替结构（图8（a～c））。此类结构一般出现在钝体绕流的剪切层和近尾迹区[21]，意味着此处存在剧烈的高低速流体动量交换。从图8（d）中可以看出，伞衣挤压机身时不会明显减弱伞衣后方的动量交换。另外，从图8（e）中还可以看到，当伞衣与机身存在较小间距时，伞衣靠近机身侧与机身之间形成通道流动，使得该处的动量交换加剧。因此，我们有理由认为伞衣与机身之间间距较小时，靠近机身的伞衣后方不会出现严重低压区（见图7），即伞衣被吸在机身上的风险较低。![]()
图 8 动载峰值时刻伞衣对称面的Lamb矢量散度云图Figure 8. Divergence of the Lamb vector at the parachute symmetrical plane涡结构的动力学特征与流场演化密切相关，涡量场的演化被涡量动力学方程所制约[22]：
\begin{split} & \frac{{{\rm{d}}{\boldsymbol{\omega}} }}{{{\rm{d}}t}} = ({\boldsymbol{\omega}} \cdot \nabla ){\boldsymbol{u}} - {\boldsymbol{\omega}} (\nabla \cdot {\boldsymbol{u}}) + \frac{1}{{{\rho ^2}}}\nabla \rho \times \nabla p + \upsilon {\nabla ^2}{\boldsymbol{\omega}} + \nabla \times {\boldsymbol{F}} \end{split} (6) 其中
({\boldsymbol{\omega}} \cdot \nabla ){\boldsymbol{u}} 表示涡线发生拉伸扭曲导致的涡量场的变化；- \omega (\nabla \cdot {\boldsymbol{u}}) 被称为散度项，表示流体体积膨胀（或压缩）导致的涡量变化；{\rho ^{ - 2}}(\nabla \rho \times \nabla p) 被称为斜压项，表示流体等密度面和等压面不重合导致的涡量变化；方程右侧第四项（黏性扩散项）和第五项（体积力项）幅值较小，涡量的影响主要集中在前三项。图9～图11给出了伞衣流场中的涡量输运项分布。不难得知，涡量的生成和输运主要发生在伞衣的近尾迹区。在三种工况下，涡拉伸/扭曲项对涡量的生成明显占主导地位，其次是散度项的影响，斜压项对涡量生成的贡献最小，这与钝体可压缩绕流的现象类似[23]。当伞衣靠近机身时，由于通道流动的存在和机身“地面效应”的影响，使得伞衣后方靠近机身侧的涡运动更加活跃。此时，涡量生成的加剧主要来源于涡拉伸/扭曲以及流体的胀压效应。这种涡运动没有导致伞衣近尾迹区产生严重低压区。Tsutsui[24]在圆球地面效应的研究中也观测到了类似的现象。由此可以得知，当伞衣靠近机身时，伞衣后方存在明显的涡运动，不会导致伞衣被吸在机身上。
![]()
图 9 伞衣对称面的涡量和涡量动力学方程中前三项的幅值({U_\infty } = 160\;{\rm{m/s}},{\rm{ }}\alpha =30^\circ )Figure 9. The magnitude of vorticity and the first three terms in the vorticity dynamics equation at the parachute symmetrical plane ({U_\infty } = 160\;{\rm{m/s}},{\rm{ }}\alpha =30^\circ) ![]()
图 11 伞衣对称面的涡量和涡量动力学方程中前三项的幅值({U_\infty } = 100\;{\rm{m/s}},{\rm{ }}\alpha =0^\circ )Figure 11. The magnitude of vorticity and the first three terms in the vorticity dynamics equation at the parachute symmetrical plane ({U_\infty } = 100\;{\rm{m/s}},{\rm{ }}\alpha =0^\circ )![]()
图 10 伞衣对称面的涡量和涡量动力学方程中前三项的幅值({U_\infty } = 100\;{\rm{m/s}},{\rm{ }}\alpha =30^\circ )Figure 10. The magnitude of vorticity and the first three terms in the vorticity dynamics equation at the parachute symmetrical plane ({U_\infty } = 100\;{\rm{m/s}},{\rm{ }}\alpha =30^\circ )3.2 伞衣充气过程
为了分析来流迎角对伞衣充气过程的影响，图12给出了来流速度100 m/s，迎角0°和30°时，伞衣在充气过程中的动载与投影面积变化。当迎角为0°时，伞衣动载和投影面积的变化曲线非常相近。说明该工况下机身对伞衣充气过程的影响较弱，伞衣充气过程与自由来流工况较为相近。当迎角为30°时，机身下方的伞衣充气速度较慢。其原因是，在充气过程的第一阶段结束时（t = 0.06 s），机身下方降落伞的底边进气口面积较小（见图13）。由于机身影响了伞衣剪切层和尾流的演化，从图13中还可以看到，机身下方的降落伞在充气过程的第三阶段中没有发生伞顶局部塌陷。这导致了伞衣投影面积和动载峰值较小。
![]()
图 12 伞衣充气过程中的动载与投影面积({U_\infty } = 100\;{\rm{m/s}} )Figure 12. The opening load and projected area during the parachute inflation process ({U_\infty } = 100\;{\rm{m/s}} )![]()
图 13 伞衣在充气过程中的外形变化({U_\infty } = 100\;{\rm{m/s}},{\rm{ }}\alpha {\rm{ = }}30^\circ )Figure 13. The canopy deformation during the parachute inflation process ({U_\infty } = 100\;{\rm{m/s}},{\rm{ }}\alpha {\rm{ = }}30^\circ )3.3 降落伞离机安全分析
降落伞安全离机主要指，1）伞衣不会受到机身影响导致开伞失败；2）降落伞离机过程中，伞衣不会剐蹭机身导致破损失效；3）降落伞离机过程中，飞机机身结构不会因为伞衣伞绳钩挂或前置体其他部件撞击导致损伤。
在伞衣充气的初始时刻，降落伞有沿z轴负方向的弹射速度
{U_{{\rm{eject}}}} 。因此在伞绳拉直的过程中，前置体质点会向z轴负方向运动。如图14（a）所示，当来流速度与弹射速度比值V = {{{U_\infty }} / {{U_{{\rm{eject}}}}}} 较小时，在充气过程中，伞衣会在机身对称面内向机身斜下方摆动并逐渐远离机身。如图14（b）所示，当来流速度增大为160 m/s时，在伞绳拉直时伞衣与机身距离较小。在充气过程中，伞衣主要沿来流方向运动更容易挤压剐蹭机身。如图14（c）所示，当弹射速度增大为20 m/s时，降落伞在充气过程中会向机身斜下方产生更大幅度的摆动，伞衣在充气过程中不会接触机身。因此可以采用增大弹射速度的方法提高降落伞离机过程的安全性。![]()
图 14 不同来流速度和弹射速度下，伞衣在充气过程中的外形变化Figure 14. The canopy deformation during the parachute inflation process at different free-stream velocities and eject velocities为了进一步分析来流速度和弹射速度对伞衣充气过程的影响，图15（a）中给出了来流迎角30°，来流速度为40 ～160 m/s时，充气过程中的动载变化。可以看到，在40 m/s和100 m/s的来流速度下，机身不会对动载峰值产生明显影响；在160 m/s的来流速度下，由于伞衣与机身发生挤压剐蹭，动载峰值明显降低。如图15（b）所示，当弹射速度增加到20 m/s时，由于伞衣不再接触机身，动载峰值与自由来流的工况几乎一致。
现代大型客机具有飞行包线保护功能，其中迎角限制是该功能中最重要的一个部分[25]。HBG系统可将超出飞行包线的状态识别为紧急状态。为避免伞衣剐蹭机身，HBG系统需要在飞机达到临界迎角前弹射降落伞。以B737的最大失速迎角作为参考[26]，以起飞安全速度（
{V_2} = 59 m/s）为最小客机飞行速度。如图16所示，随着来流速度增加，HBG系统安全离机的临界迎角下降。飞机失速迎角与HBG系统临界迎角共同组成了HBG系统的工作包线（图16中黑色虚线区域）。随着来流速度增加，可供HBG系统工作的来流迎角范围不断减小。考虑到在相同来流工况下，降落伞弹射离机的速度越大，在伞绳拉直时降落伞与机身的距离就越远。所以为了增大HBG系统的适用范围，可以采用提高降落伞弹射速度的方法。当弹射速度从10 m/s提高到20 m/s时，临界迎角大幅提高，使HBG系统获得了更大的适用范围。4. 结 论
现有研究主要关注大尺寸降落伞的充气过程，本文考虑了飞机机身下方小型降落伞的离机充气过程。分析了机身、来流速度和来流角度对开伞过程的影响，计算了不同速度下降落伞安全离机的最小来流迎角，得到了如下结论：
1）在开伞过程中，当伞衣贴近机身时，靠近机身的伞衣后方不会出现严重低压区，即伞衣被吸在机身上的风险较低，开伞失败的风险较低。
2）当来流速度与弹射速度比值较大时，伞衣更容易挤压剐蹭机身。可以通过有限增加降落伞弹射速度的方法，提高降落伞离机过程的安全性。
3）当来流速度不变时，存在降落伞在离机过程中安全临界迎角。在40～160 m/s来流速度范围内，来流速度越大临界迎角越小。提高降落伞弹射速度可以增大临界迎角。
下一步工作可针对机身表面较小的凸起或尖锐物等结构进行研究，分析不同工况下机身表面凸起结构是否会钩挂伞衣，影响降落伞离机过程的安全性。
-
![]()
图 2 试验和数值模拟中的开伞动载
Figure 2. The parachute opening loads in experiments and numerical simulation
![]()
图 5 降落伞与机身尾部相对位置示意图
Figure 5. Schematic diagram of the relative position between a parachute and a fuselage tail
![]()
图 6 动载峰值时刻伞衣与机身的距离
Figure 6. The distance between a parachute and a fuselage when the opening load reaches its maximum
![]()
图 7 动载峰值时刻伞衣对称面的压力云图，等值线为流向速度
Figure 7. Flow fields at the parachute symmetrical plane (Shade and line contours denote pressure and streamwise velocity, respectively)
![]()
图 8 动载峰值时刻伞衣对称面的Lamb矢量散度云图
Figure 8. Divergence of the Lamb vector at the parachute symmetrical plane
![]()
图 9 伞衣对称面的涡量和涡量动力学方程中前三项的幅值(
{U_\infty } = 160\;{\rm{m/s}},{\rm{ }}\alpha =30^\circ )Figure 9. The magnitude of vorticity and the first three terms in the vorticity dynamics equation at the parachute symmetrical plane (
{U_\infty } = 160\;{\rm{m/s}},{\rm{ }}\alpha =30^\circ) ![]()
图 11 伞衣对称面的涡量和涡量动力学方程中前三项的幅值(
{U_\infty } = 100\;{\rm{m/s}},{\rm{ }}\alpha =0^\circ )Figure 11. The magnitude of vorticity and the first three terms in the vorticity dynamics equation at the parachute symmetrical plane (
{U_\infty } = 100\;{\rm{m/s}},{\rm{ }}\alpha =0^\circ )![]()
图 10 伞衣对称面的涡量和涡量动力学方程中前三项的幅值(
{U_\infty } = 100\;{\rm{m/s}},{\rm{ }}\alpha =30^\circ )Figure 10. The magnitude of vorticity and the first three terms in the vorticity dynamics equation at the parachute symmetrical plane (
{U_\infty } = 100\;{\rm{m/s}},{\rm{ }}\alpha =30^\circ )![]()
图 12 伞衣充气过程中的动载与投影面积(
{U_\infty } = 100\;{\rm{m/s}} )Figure 12. The opening load and projected area during the parachute inflation process (
{U_\infty } = 100\;{\rm{m/s}} )![]()
图 13 伞衣在充气过程中的外形变化(
{U_\infty } = 100\;{\rm{m/s}},{\rm{ }}\alpha {\rm{ = }}30^\circ )Figure 13. The canopy deformation during the parachute inflation process (
{U_\infty } = 100\;{\rm{m/s}},{\rm{ }}\alpha {\rm{ = }}30^\circ )![]()
图 14 不同来流速度和弹射速度下，伞衣在充气过程中的外形变化
Figure 14. The canopy deformation during the parachute inflation process at different free-stream velocities and eject velocities
-
[1] YE W, SUN J H. Emergency mechanical and communication systems and methods for aircraft: US9440749[P]. 2016-09-13.
[2] YE W, SUN J H. Emergency mechanical and communication systems and methods for aircraft: US9452844[P]. 2016-09-27.
[3] YE W, SUN J H. Emergency mechanical and communication systems and methods for aircraft: US9771160[P]. 2017-09-26.
[4] 张延泰, 孙建红, 侯斌, 王一波. 分离式飞机应急记录跟踪系统设计与试验[J]. 北京航空航天大学学报(已录用). ZHANG Y T, SUN J H, HOU B, WANG Y B. Design and test of ejection flight data recording and emergency tracking system[J]. Journal of Beijing University of Aeronautics and Astronautics(in press).
[5] 刘洋, 周星. 民用飞机试飞员空中应急离机轨迹风洞实验研究[J]. 实验流体力学, 2015, 29(6): 54-58. doi: 10.11729/syltlx20140066 LIU Y, ZHOU X. Investigation of flight test crew aerial emergency egress trajectory from civil aircraft in low speed wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(6): 54-58. (in Chinese)DOI: 10.11729/syltlx20140066[万方].
[6] 刘晓宇, 桑为民, 鲁天, 等. 人员离机轨迹数值模拟及快速预测研究[J]. 航空工程进展, 2014, 5(2): 220-226. doi: 10.3969/j.issn.1674-8190.2014.02.015 LIU X Y, SANG W M, LU T, et al. Numerical simulation and quick prediction of men's separation trajectory[J]. Advances in Aeronautical Science and Engineering, 2014, 5(2): 220-226. (in Chinese)DOI: 10.3969/j.issn.1674-8190.2014.02.015[万方].
[7] BERGMANN A, LOESER T. Capabilities of Deployment Tests at DNW-NWB[C]//Meeting paper for US Defense Technical Information Center. 2006.
[8] SCHADE N, GEISBAUER S, SCHMIDT H, et al. Experimental and numerical investigation of the flow topology during airdrop operations[C]//21st AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Dublin, Ireland. Reston, Virigina: AIAA, 2011: 2565. doi: 10.2514/6.2011-2565
[9] ROOSENBOOM E W M, SCHROEDER A, GEISLER R, et al. Experimental investigation of the flow field topology for several cargo drop configurations[C]//28th Aerodynamic Measurement Technology, Ground Testing, and Flight Testing Conference, New Orleans, Louisiana. Reston, Virginia: AIAA, 2012. doi: 10.2514/6.2012-3198
[10] GEISBAUER S, BIER N, KIRZ J, et al. Validation of the flow topology around several airdrop cargo configurations at static conditions[C]//31st AIAA Applied Aerodynamics Conference, San Diego, CA. Reston, Virginia: AIAA, 2013: 3155. doi: 10.2514/6.2013-3155
[11] TEZDUYAR T, OSAWA Y. The multi-domain method for computation of the aerodynamics of a parachute crossing the far wake of an aircraft[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 191(6-7): 705-716.DOI: 10.1016/S0045-7825(01)00310-3[LinkOut].
[12] SERRANO M, LEIGH E, JOHNSON W, et al. Computational aerodynamics of the C-130 in airdrop configurations[C]//41st Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virigina: AIAA, 2003: 229. doi: 10.2514/6.2003-229
[13] GHOREYSHI M, ROSE T, LARSEN E, et al. Dynamic simulation and analysis of personnel airborne exits[C]//AIAA AVIATION 2020 FORUM, VIRTUAL EVENT. Reston, Virginia: AIAA, 2020. doi:10.2514/6.2020-2704
[14] BERGERON K, GHOREYSHI M, LARSEN E, et al. Near-body/Cartesian off-body simulations for C-17 and extraction parachute[C]//AIAA AVIATION 2020 FORUM, VIRTUAL EVENT. Reston, Virginia: AIAA, 2020. doi: 10.2514/6.2020-2712
[15] HEINRICH H G, NOREEN R A. Analysis of parachute opening dynamics with supporting wind-tunnel experiments[J]. Journal of Aircraft, 1970, 7(4): 341-347.DOI: 10.2514/3.44175[LinkOut].
[16] 喻东明, 李丰雄. 随机变量总体均值在降落伞技术中的应用[J]. 航空学报, 1999, 20(S1): 3-5. YU D M, LI F X. Application of population mean of random variables to parachute technology[J]. Acta Aeronautica et Astronautica Sinica, 1999, 20(S1): 3-5. (in Chinese)[知网].
[17] JOHARI H, DESABRAIS K J. Vortex shedding in the near wake of a parachute canopy[J]. Journal of Fluid Mechanics, 2005, 536: 185. doi: 10.1017/S0022112005004490
[18] HAMMAN C W, KLEWICKI J C, KIRBY R M. On the Lamb vector divergence in Navier–Stokes flows[J]. Journal of Fluid Mechanics, 2008, 610: 261-284. doi: 10.1017/S0022112008002760
[19] FANG M, SUN J H, ZHANG T, HOU B, ZHANG Y T. Flow characteristics of double-cruciform parachute at inflating and inflated conditions[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2018, 35(6): 992-999.
[20] 许常悦, 郑静, 王哲, 王彬. 方柱跨声速流动中的剪切层和尾迹特性[J], 上海交通大学学报, 2020. XU C Y, ZHENG J, WANG Z, WANG B. The shear layer and wake characteristics of square cylinder in the transonic flow[J]. Journal of Shanghai Jiaotong University, 2020.
[21] 许常悦, 王从磊, 孙建红. 圆柱跨声速绕流中的激波/湍流相互作用大涡模拟研究[J]. 空气动力学学报, 2012, 30(1): 22-27, 51. XU C Y, WANG C L, SUN J H. Large eddy simulation of shock-wave/turbulence interaction in the transonic flow over a circular cylinder[J]. Acta Aerodynamica Sinica, 2012, 30(1): 22-27, 51. (in Chinese)[知网].
[22] 庄礼贤, 尹协远, 马晖扬. 流体力学[M]. 2版. 合肥: 中国科学技术大学出版社, 2009. ZHUANG L X, YIN X Y, MA H Y. Fluid mechanics[M]. Hefei: University of Science and Technology of China Press, 2009. (in Chinese)
[23] 许常悦. 圆柱可压缩绕流及其流动控制的大涡模拟研究[D]. 合肥: 中国科学技术大学, 2009. XU C Y. Large eddy simulation of the compressible flow past a circular cylinder and its flow control[D]. Hefei: University of Science and Technology of China, 2009. (in Chinese).
[24] TSUTSUI T. Flow around a sphere in a plane turbulent boundary layer[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(6-7): 779-792.DOI: 10.1016/j.jweia.2007.06.031[LinkOut].
[25] 刘天宇, 夏洁, 钱艳平. 大型飞机迎角限制器设计与飞行品质评估[J]. 系统仿真学报, 2011, 23(S1): 215-218. doi: 10.16182/j.cnki.joss.2011.s1.016 LIU T Y, XIA J, QIAN Y P. Design of limiters for attack angle of large aircraft and flying qualities evaluation[J]. Journal of System Simulation, 2011, 23(S1): 215-218. (in Chinese)DOI: 10.16182/j.cnki.joss.2011.s1.016[知网].
[26] Boeing 737-800 Aircraft Maintenance Manual[M]. Seatle, Washington, USA: Boeing Comercial Airplanes Group, 1998.
-
期刊类型引用(1)
1. 张延泰，孙建红，侯斌. 小型降落伞充气和伞衣塌陷过程. 天津师范大学学报(自然科学版). 2022(04): 23-30 . 
百度学术
其他类型引用(4)
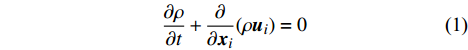
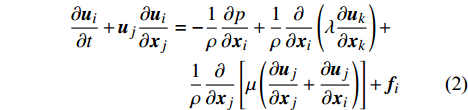
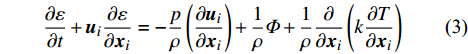
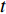
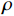
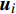
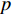
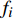
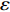
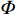
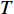
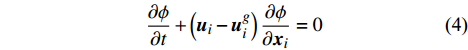
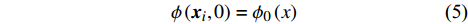
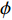
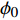
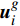
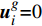
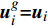
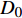
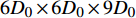
下载:
计量
- 文章访问数: 330
- HTML全文浏览量: 161
- PDF下载量: 48
- 被引次数: 5
