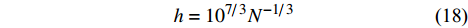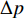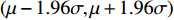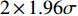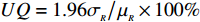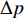Sonic boom prediction and uncertainly quantification analysis of a low-boom super-sonic aircraft
-
摘要: 声爆精确预测问题是制约超声速客机技术突破的关键瓶颈之一。由于大气来流条件不断发生波动存在不确定性,为得到更可靠的声爆近/远场信号,需考虑来流参数的不确定性对声爆预测结果的影响,并甄别其中影响声爆预测的关键性因素,为工程实际应用提供有价值的参考。本文基于CFD声爆近场信号模拟和增广Burgers方程的声爆远场信号预测方法,对第三届声爆预测研讨会(SBPW-3)的C608低声爆超声速飞行器开展了声爆信号特性分析。首先,采用约5021万非结构混合网格半模计算了近场过压值,并研究了远场地面波形计算的时间和空间网格收敛性。接着,分析了基准状态下复杂近场流动特征及地面波形特征,通过与C608飞行器公开数据对比,验证了该方法和自研程序的准确度。此外,研究了不同物理模型和大气相对湿度对地面波形的影响。在此基础上,运用基于非嵌入式多项式混沌(NIPC)方法开展了对不同来流参数(来流马赫数、来流攻角和单位雷诺数)的不确定度量化分析和敏感性分析。结果表明,在给定的输入变量不确定度条件下,地面波形波峰与波谷处过压值变化明显。相比而言,来流单位雷诺数对地面波形过压值的影响显著低于来流马赫数和来流攻角的影响。Abstract: Accurate prediction of sonic booms is one of the key bottlenecks restricting the breakthrough of supersonic aircraft technology. To obtain a more reliable near- and far-field signals of a sonic boom, it is necessary to consider the influence of the uncertainty of incoming flow parameters that fluctuate continuously. Moreover, key factors affecting the accurate prediction of sonic booms need to be identified to provide a valuable guideline for practical applications. In this paper, the sonic boom characteristics of the supersonic aircraft C608 provided by the 3rd sonic boom prediction workshop (SBPW-3) are analyzed based on the near-field signal simulation based on Computational Fluid Dynamics and the far-field signal prediction method based on the augmented Burgers equation. Firstly, the near-field over-pressure value is calculated using an unstructured hybrid grid with 50.21 million cells for half of the model, and the temporal and spatial grid convergence of far-field ground waveform is studied. Secondly, the complex near-field flow characteristics and ground waveform characteristics in the reference state are analyzed. Compared with the public data of aircraft C608, the accuracy of the method and the in-house-development program has been effectively verified. In addition, the effects of different physical models and atmospheric relative humidity on the ground waveform are also investigated. On this basis, the uncertainty quantification and sensitivity analysis of different incoming flow parameters (Mach number, angle of attack, and unit Reynolds number) are carried out by using the non-intrusive polynomial chaos (NIPC) and Sobol index method. The results show that, for a given uncertainty of input variables, the over-pressure values at the peak and trough of ground waveform differ significantly. In contrast, the influence of unit Reynolds number is significantly smaller than those of Mach number and angle of attack.
-
0. 引 言
随着全球化的发展,利用超声速客机可以极大缩短国际航线的飞行时间,积极发展新一代超声速客机,有望极大促进我国同世界各国在经济、文化等各领域的交流与合作,促进全球化进程不断深入。
为了充分发挥超声速客机的速度优势,未来的超声速客机必须具备陆地上空超声速巡航能力。但超声速客机投入运营仍存在种种阻碍因素,其中声爆噪声显得尤为突出。因此低声爆/低噪声成为未来超声速客机的重要设计指标之一。
20世纪50年代 ,声爆现象首次得到关注,相关研究人员对其开展了初步研究。Whitham针对此现象,首次提出了基于线化理论的声爆预测方法[1]。在1965~1970年间,NASA举办了三届声爆研讨会[2-4],借此推动深刻理解声爆的产生、传播、预测和最小化问题。
21世纪,声爆预测和低声爆超声速客机的研究在国际上重新掀起热潮。2014年,AIAA举办了第一届声爆预测研讨会[5],评估了当前近场声爆信号的计算精度,为远场声爆预测打下基础。2017年,AIAA举办了第二届声爆预测研讨会[6],该研讨会同时将近场过压值信号的计算和远场地面波形的预测作为重点。2020年,AIAA举办了第三届声爆预测研讨会[7-8],该研讨会主要将C608低声爆超声速飞行器作为标准算例,讨论先进的近场CFD声爆信号预测方法及远场地面波形预测方法,及其在具有复杂推进和环境控制系统条件下的低声爆外形计算中的适应性。
目前对声爆的研究主要包括两方面,声爆预测以及低声爆设计。其中声爆预测是指对飞机超声速飞行时产生的声爆水平进行评估,包括对近场、中场以及远场地面的声爆水平进行计算[7-9]。而低声爆设计是指通过一定的方式对飞行器超声速飞行时的声爆水平进行控制,使其处于能够接受的范围[10]。
声爆预测方法大致分为三类:基于线性理论的声爆快速预测方法[11];基于近场CFD与远场非线性传播方程的声爆高精度预测方法[12]以及全场CFD数值模拟方法[13]。其中,基于近场CFD与远场非线性传播方程的声爆高精度预测方法是当前更为合适的声爆预测方法,其优势在于:一是相比于线性理论,该方法能够计算复杂外形的声爆特征,同时结合增广Burgers方程还可以较准确地计算声爆的上升时间;二是相对于全场CFD数值模拟,该方法大大降低了计算量,同时还合理地考虑了真实大气环境中的分子弛豫、热黏性吸收等效应。
近年来,声爆的相关研究在国内也逐渐得到重视。朱自强和兰世隆[14]指出,高精度流场模拟和基于非线性声学的增广Burgers方程等方法在声爆预测中的优势。张绎典等[15]建立了增广Burgers方程的数值求解方法,并提出了一些方法来提高过压值、上升时间等关键参数的计算精度。
超声速客机在飞行过程中,由于飞行高度和大气密度等经常发生波动,大气来流条件也随之不断发生变化。为得到更可靠的低声爆近/远场信号预测结果,在考虑计算网格、物理模型及相对湿度等对声爆近/远场信号预测的影响的基础上, 也需要考虑来流参数的不确定性和由此带来的声爆近/远场信号预测的不确定度。目前,国内外对于考虑来流不确定性的低声爆超声速客机近/远场信号预测的相关研究还较少。
针对CFD不确定度量化分析问题,多项式混沌方法[16]得到了广泛应用。本文拟采用基于非嵌入式多项式的混沌方法(non-intrusive polynomial chaos, NIPC)开展不确定度量化分析研究,即选择一组正交多项式作为空间的无限基函数,将变量分解为确定和随机两部分,从而构造出多项式混沌展开式。该方法将CFD求解器当做黑盒子,基于确定性的解来近似多项式混沌展开式的系数,并在非嵌入式多项式混沌方法的基础上,采用Sobol指数来衡量输入变量的敏感性。
本文拟以AIAA第三届声爆预测会标模C608低声爆超声速飞行器[8, 17]为研究对象,开展复杂外形声爆近/远场信号特征分析及不确定度量化分析,以期为超声速客机低声爆设计提供参考依据,并进一步用于超声速客机的鲁棒优化设计及可靠性分析。
1. 数值方法
1.1 声爆近场预测方法
在声爆计算体系下,采用基于Naiver-Stokes方程的CFD方法来计算近场过压值分布,从而为声爆传播方程提供输入信号以计算远场地面信号。
在笛卡尔坐标系下,同时忽略体积力(如重力、电磁力等)和外部热源,守恒形式的三维非定常可压缩Naiver-Stokes方程可表示为[18]:
\frac{{\partial {\boldsymbol{Q}}}}{{\partial t}} + \frac{{\partial {\boldsymbol{f}}}}{{\partial x}} + \frac{{\partial {\boldsymbol{g}}}}{{\partial y}} + \frac{{\partial {\boldsymbol{h}}}}{{\partial z}} = 0 (1) 式中:
{\boldsymbol{Q}} 为守恒变量;{\boldsymbol{f}}、{\boldsymbol{g}}、{\boldsymbol{h}} 分别为三个坐标方向的通量,可表示为:{\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} \rho \\ {\rho u} \\ {\rho v} \\ {\rho w} \\ {\rho e} \end{array}} \right] (2) {\boldsymbol{f}} = \left[ {\begin{array}{*{20}{c}} {\rho u} \\ {\rho {u^2} + p - {\tau _{xx}}} \\ {\rho uv - {\tau _{xy}}} \\ {\rho uw - {\tau _{xz}}} \\ {\left( {\rho e + p} \right)u - u{\tau _{xx}} - v{\tau _{xy}} - w{\tau _{xz}} + {q_x}} \end{array}} \right] (3) {\boldsymbol{g}} = \left[ {\begin{array}{*{20}{c}} {\rho v} \\ {\rho uv - {\tau _{xy}}} \\ {\rho {v^2} + p - {\tau _{yy}}} \\ {\rho vw - {\tau _{yz}}} \\ {\left( {\rho e + p} \right)v - u{\tau _{xy}} - v{\tau _{yy}} - w{\tau _{yz}} + {q_y}} \end{array}} \right] (4) {\boldsymbol{h}} = \left[ {\begin{array}{*{20}{c}} {\rho w} \\ {\rho uw - {\tau _{xz}}} \\ {\rho vw - {\tau _{yz}}} \\ {\rho {w^2} + p - {\tau _{zz}}} \\ {\left( {\rho e + p} \right)w - u{\tau _{xz}} - v{\tau _{yz}} - w{\tau _{zz}} + {q_z}} \end{array}} \right] (5) 式中:
\;\rho 为密度;u、v、w 为笛卡尔坐标系下的速度分量;{\tau _{xx}}、{\tau _{yy}}、{\tau _{zz}}、{\tau _{xy}}、{\tau _{xz}}、{\tau _{yz}} 为黏性应力项;e 为单位质量气体的总能量;p 为压力;{q_x}、{q_y}、{q_z} 分别为三个坐标方向的热流量。1.2 声爆远场预测方法
在声爆计算体系下,采用基于非线性声学理论的增广Burgers方程方法将近场波形推进到远场,从而求解地面声爆信号。
20世纪60年代,Blackstock[19]最早使用Burgers方程来模拟波在有损耗介质中的传播,提出了经典Burgers方程[20],其形式如下:
\frac{\partial p'}{\partial x}-\frac{\beta }{2{\rho }_{0}{c}_{0}^{3}}\frac{\partial p{'}^{2}}{\partial t'} = \frac{b}{2{\rho }_{0}{c}_{0}^{3}}\frac{{\partial }^{2}p'}{\partial t{'}^{2}} (6) 在经典Burgers方程中加入非均匀介质、几何扩散以及分子弛豫效应的影响,即可得到增广Burgers方程[21]:
\begin{split}\frac{\partial p'}{\partial x} =& \frac{\beta }{2{\rho }_{0}{c}_{0}^{3}}\frac{\partial p{'}^{2}}{\partial t'}+\frac{b}{2{\rho }_{0}{c}_{0}^{3}}\frac{{\partial }^{2}p'}{\partial t{'}^{2}}+\frac{1}{2{\rho }_{0}{c}_{0}}\frac{\partial \left({\rho }_{0}{c}_{0}\right)}{\partial x}p'-\\ & \frac{1}{2S}\frac{\partial S}{\partial x}p'+{\displaystyle \sum _{{\nu} }\frac{{\left(\Delta c\right)}_{{\nu} }{\tau }_{{\nu} }}{{c}_{0}^{2}}{\left(1+{\tau }_{{\nu} }\frac{\partial }{\partial t'}\right)}^{-1}\frac{{\partial }^{2}p'}{\partial t{'}^{2}}}\end{split} (7) 式中:
S 为声管面积[22];{\left( {\Delta c} \right)_{\nu} } 为分子弛豫效应造成的声速变化量;{\tau _{\nu} } 为弛豫时间,下标{\nu} 表示不同的大气组分(如O2、N2)的弛豫过程。式(7)等号右边5项分别对应非线性效应、经典吸收、大气分层、几何扩散以及分子弛豫效应对声爆的影响。为了便于求解,对式(7)进行无量纲化处理:
\begin{split}\frac{\partial P}{\partial \sigma } =& P\frac{\partial P}{\partial \tau }+\frac{1}{\varGamma }\frac{{\partial }^{2}P}{\partial {\tau }^{2}}+\frac{1}{2{\rho }_{0}{c}_{0}}\frac{\partial {\rho }_{0}{c}_{0}}{\partial \sigma }P-\\& \frac{1}{2S}\frac{\partial S}{\partial \sigma }P+{\displaystyle \sum _{v}{C}_{v}\frac{{\partial }^{2}/\partial {\tau }^{2}}{1+{\theta }_{v}(\partial /{\partial }_{\tau })}}P\end{split} (8) 式中:
P = {{p'} \mathord{\left/ {\vphantom {{p'} {{p_0}}}} \right. } {{p_0}}} ,{p_0} 为参考气压;无量纲距离\sigma = {x \mathord{\left/ {\vphantom {x {\bar x}}} \right. } {\bar x}} ,参考距离为\bar x = {{{\rho _0}c_0^3} \mathord{\left/ {\vphantom {{{\rho _0}c_0^3} {\left( {\beta {\omega _0}{p_0}} \right)}}} \right. } {\left( {\beta {\omega _0}{p_0}} \right)}} ;无量纲时间\tau = {\omega _0}t' ,参考时间为{1 \mathord{\left/ {\vphantom {1 {{\omega _0}}}} \right. } {{\omega _0}}} ,可由输入信号采样率决定;无量纲耗散参数\varGamma {\text{ = }}{{{b}{\omega _0}} \mathord{\left/ {\vphantom {{{b}{\omega _0}} {\left( {2\beta {p_0}} \right)}}} \right. } {\left( {2\beta {p_0}} \right)}} ;无量纲弛豫时间{\theta _{\nu} } = {\omega _0}{\tau _{\nu} } ;无量纲弛豫系数{C_v} = {{{m_{\nu} }{\tau _{\nu} }\omega _0^2\bar x} \mathord{\left/ {\vphantom {{{m_{\nu} }{\tau _{\nu} }\omega _0^2\bar x} {\left( {2{c_0}} \right)}}} \right. } {\left( {2{c_0}} \right)}} ,{m_{\nu} } = {{2{{\left( {\Delta c} \right)}_{\nu} }} \mathord{\left/ {\vphantom {{2{{\left( {\Delta c} \right)}_{\nu} }} {{c_0}}}} \right. } {{c_0}}} 。1.3 混沌多项式不确定性分析
在考虑来流不确定性的低声爆超声速客机近/远场信号不确定度量化分析中,以地面波形过压值
\Delta p 等声爆重要参数作为随机输出变量,表示为:{\alpha ^*}\left( {{\boldsymbol{x}},{\boldsymbol{\xi}} } \right) \approx \sum\limits_{j = 0}^P {{\alpha _j}\left( {\boldsymbol{x}} \right){\psi _j}\left( {\boldsymbol{\xi}} \right)} (9) 式中:
{\alpha ^*} 是CFD方法或增广Burgers方程计算结果;{\alpha _j}\left( {\boldsymbol{x}} \right) 是计算结果的确定部分耦合系数;随机部分{\psi _j}\left( {\boldsymbol{\xi}} \right) 是以n维随机变量{{\boldsymbol{\xi}}} \text{ = }\left({\xi }_{1},\cdots ,{{\xi} }_{n}\right) 为自变量的随机函数,为{\boldsymbol{\xi}} 的正交多项式。式(9)可将任一随机变量分解为确定和随机两个独立部分。出于计算量的考虑,对
{\psi _j}\left( {\boldsymbol{\xi}} \right) 多项式采取r阶截断,设随机参数的维数为n,则混沌多项式(PCE)项数可以表示为[23]:N_t = R+ 1 = \frac{{\left( {n + r} \right)!}}{{n!r!}} (10) 根据随机变量
{\boldsymbol{\xi}} 的分布,即输入参数的分布类型不同,对随机变量{\psi _j}\left( {\boldsymbol{\xi}} \right) 选取不同形式的正交多项式。当输入参数服从正态分布时,选取Hermite正交多项式;当输入参数服从均匀分布时,选取Legendre正交多项式[23]。目前,主要有两种形式的基于非嵌入式混沌多项式(NIPC)的不确定度分析方法:随机响应面法(stochastic response surface method, SRSM)和基于Galerkin的投影法。本文采用随机响应面法来求解正交多项式系数,开展不确定度分析。
通常采用过采样策略。文献[24]中推荐选用PCE系数两倍的过采样方法,即
N = 2N_t = 2\left( {R + 1} \right) 。根据Schaefer等[25]的比较结果,采用精度和收敛性均表现较好的拉丁超立方(Latin hypercube design, LHD)抽样方法,对模型参数进行抽样选取。采用最小二次回归求解PCE系数,将样本
{\boldsymbol{\xi}} = {\left[ {{\xi _1}, \cdots ,{\xi _j}, \cdots ,{\xi _N}} \right]^{\rm{T}}} 和相应的函数响应值{\boldsymbol{G}} = {\Big[ {g\Big( {{x_1}} \Big), \cdots ,}} {{g\Big( {{x_{_N}}} \Big)} \Big]^{\rm{T}}} 分别代入PCE模型,得到:\begin{split} \left[ {\begin{array}{*{20}{c}} {{\psi _0}\left( {{\xi _1}} \right)}&{{\psi _1}\left( {{\xi _1}} \right)}& \cdots &{{\psi _R}\left( {{\xi _1}} \right)} \\ {{\psi _0}\left( {{\xi _2}} \right)}&{{\psi _1}\left( {{\xi _2}} \right)}& \cdots &{{\psi _R}\left( {{\xi _2}} \right)} \\ \vdots & \vdots & \ddots & \cdots \\ {{\psi _0}\left( {{\xi _N}} \right)}&{{\psi _1}\left( {{\xi _N}} \right)}& \cdots &{{\psi _R}\left( {{\xi _N}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\alpha _0}} \\ {{\alpha _1}} \\ \vdots \\ {{\alpha _R}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {g\left( {{x_1}} \right)} \\ {g\left( {{x_2}} \right)} \\ \vdots \\ {g\left( {{{x_{_N}}}} \right)} \end{array}} \right]\\ \end{split} (11) 定义
J\left( \alpha \right) = \sum\limits_{j = 1}^N {\varepsilon _j^2} = \sum\limits_{j = 1}^N {{{\left[ {g\left( {{x_j}} \right) - \hat g\left( {{\xi _j}} \right)} \right]}^2}} (12) 式中,
\hat g\left( {{\xi _j}} \right) = \displaystyle\sum\limits_{j = 0}^P {{\alpha _j}\left( { {\boldsymbol{x}}} \right){\psi _j}\left( { {\boldsymbol{\xi}} } \right)} ,即基于PCE模型估算出的各样本点上的函数响应值。利用线性最小二次回归,使
J\left( \alpha \right) 最小,求解得到PCE系数{\alpha _j} 的值,同时可以由展开式系数直接计算输出响应的均值\mu 和方差D 等概率统计量,如下所示:\begin{split}&\qquad {{\mu _{_R}} = {\alpha _0}} \\& {{D_R} = \sum\limits_{j = 1}^P {\alpha _j^2\left[ {\psi _j^2\left( {\boldsymbol{\xi}} \right)} \right]} } \end{split} (13) 使用敏感度指标来表征不同随机输入对模型响应输出的影响程度。本文采用可以直接从多项式混沌展开式中得到的Sobol敏感度指标,开展基于方差分解的全局敏感度分析。
将多项式混沌展开式重新分解,得到总方差为:
D = \sum\limits_{i = 1}^n {{D_i}} {\text{ + }}\sum\limits_{1 \leqslant i < j \leqslant n}^{n-1} {{D_{i,j}}} + \sum\limits_{1 \leqslant i < j < k \leqslant n}^{n{{ - 2}}} {{D_{i,j,k}}} + \cdots + {D_{1,2, \cdots ,n}} (14) 部分方差为:
{D_{{i_1}, \cdots ,{i_s}}} = \sum\limits_{\beta \in \left\{ {{i_1}, \cdots ,{i_s}} \right\}} {\alpha _\beta ^2\left[ {\psi _\beta ^2\left( {\boldsymbol{\xi}} \right)} \right],\;\;{\text{ }}1 \leqslant {i_1} < \cdots < {i_s} \leqslant n} (15) 则Sobol指数作为敏感性指数定义为部分方差与总方差的比值:
{S_{{i_1} \cdots {i_s}}} = \frac{{{D_{{i_1} \cdots {i_s}}}}}{D} (16) 另外,针对输入参数i的Sobol指数(
{S_{Ti}} )则定义为包含变量i的所有部分Sobol指数之和:{S_{ Ti}} = \sum\limits_{Li} {\frac{{{D_{{i_1} \cdots {i_s}}}}}{D},\;\;{\text{ }}{L_i} = \left\{ {\left( {{i_1} \cdots {i_s}} \right):\exists k,\;\;1 \leqslant k \leqslant s,\;\;{i_k} = i} \right\}} (17) Sobol指数的详细推导过程和具体形式可以参阅文献[26]。
2. 模型介绍及程序验证
2.1 C608飞行器外形及来流条件
采用美国AIAA第三届声爆预测研讨会(SBPW-3,2020)提供的C608飞行器标准算例开展研究[7]。C608是NASA低声爆试验飞行器X59的初步改形方案,其来自于洛克希德·马丁公司对NASA N+2超声速客机概念设计研究。三维视图如图1所示。
C608飞行器参考长度L = 27.432 m,半模参考面积s = 37.16 m2,来流条件和边界条件如表1所示。C608具有推进和环境控制系统(environmental control system, ECS)。
表 1 C608来流和边界条件Table 1. Freestream and boundary conditions of C608参 数 量 值 来流马赫数 1.4 来流攻角/(°) 0 来流温度/K 216.61 飞行高度/m 16215.36 单位雷诺数/(m–1) 4321890 发动机喷嘴增压室总压与来流静压之比 10.0 发动机喷嘴增压室总温与来流静温之比 7.0 发动机旁路排气总压与来流静压之比 2.4 发动机旁路排气总温与来流静温之比 2.0 发动机风扇表面静压与来流静压之比 2.6 环境控制系统入口静压与来流静压之比 1.4 2.2 网格收敛性研究
声爆近场输入信号计算采用自研CFD软件[27-28],湍流模型为SA模型,近场距离为3个C608飞行器长度(z = 82.29 m)。网格使用SBPW-3提供的非结构混合网格[7],半模网格节点数约5021万,特征网格尺度h定义为:
h = {10^{{7 \mathord{\left/ {\vphantom {7 3}} \right. } 3}}}{N^{ - {1 \mathord{\left/ {\vphantom {1 3}} \right. } 3}}} (18) 当此特征网格尺度h = 0.58时,网格具有较好的收敛性。具体网格细节见表2。
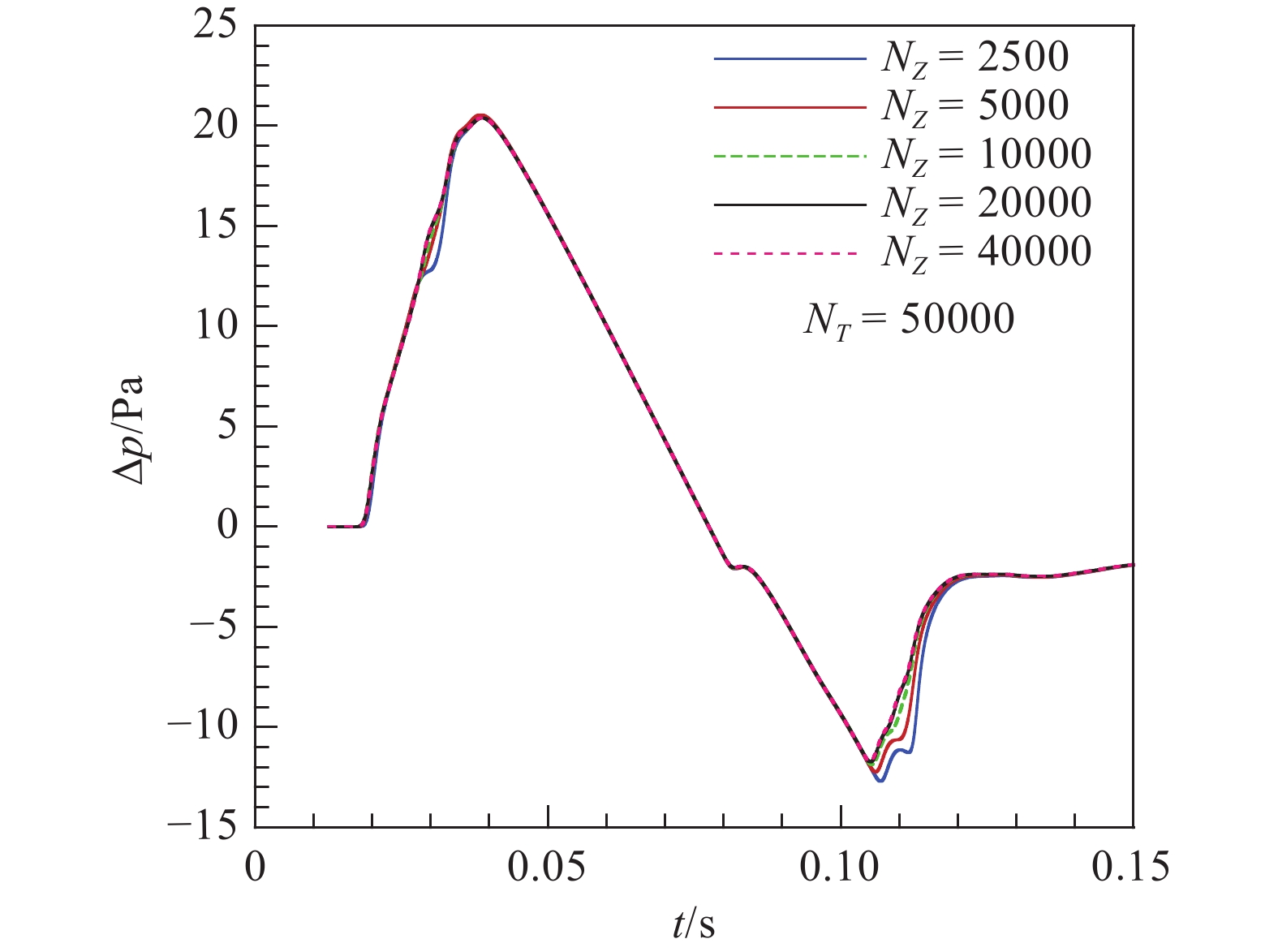
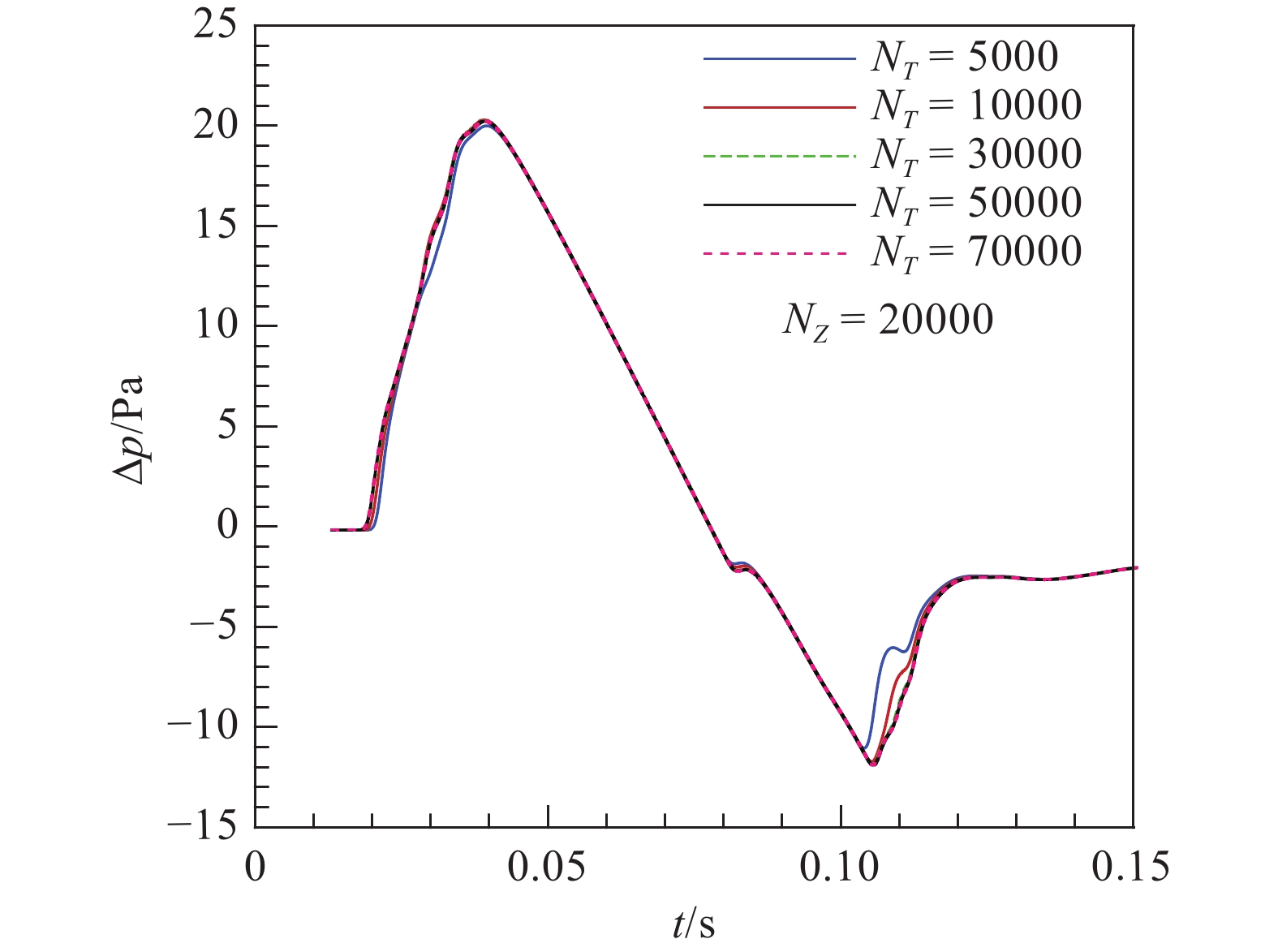
表 2 非结构混合网格Table 2. Unstructured hybrid grid网格名称 特征网格尺度 节点数 单元数 四面体 棱柱 Mix-064 0.58 50215130 36567810 86083502 远场地面波形计算利用自研声爆程序[15]。选取上述CFD计算所得到的近场过压值分布作为输入信号,利用增广Burgers方程计算远场地面波形。由于增广Burgers方程具有两个维度(时间维度和空间维度),在进行网格收敛性研究时需要依次对这两个维度展开分析。在均匀网格下,采用不同空间网格密度和时间网格密度,具体网格量见表3和表4。表中,NZ为空间网格点数,NT为时间网格点数。也可用时间采样率表示时间网格密度。
表 3 不同空间网格密度Table 3. Different spatial grid sizes算例 空间网格点数 时间网格点数 采样率/kHz 1 2500 50000 335.94 2 5000 50000 335.94 3 10000 50000 335.94 4 20000 50000 335.94 5 40000 50000 335.94 表 4 不同时间网格密度Table 4. Different temporal grid sizes算例 空间网格点数 时间网格点数 采样率/kHz 1 20000 5000 33.59 2 20000 10000 67.19 3 20000 30000 201.56 4 20000 50000 335.94 5 20000 70000 470.32 图2和图3分别给了出远场地面波形在空间和时间维度上的网格收敛性。由图可见,地面波形对空间和时间网格密度都有一定敏感性,但需要加密到一定程度后,远场地面波形信号才能逐渐收敛。对于该算例,当空间网格密度和时间网格密度分别达到20000点和30000点以后,网格达到收敛,此后地面波形基本不随网格密度变化。
综上所示,利用增广Burgers方程计算远场地面波形时,需适当加密网格。基于上述分析,本文选用网格NZ = 20000和NT = 50000开展研究。
3. 基准状态分析
3.1 基准状态近/远场信号分析
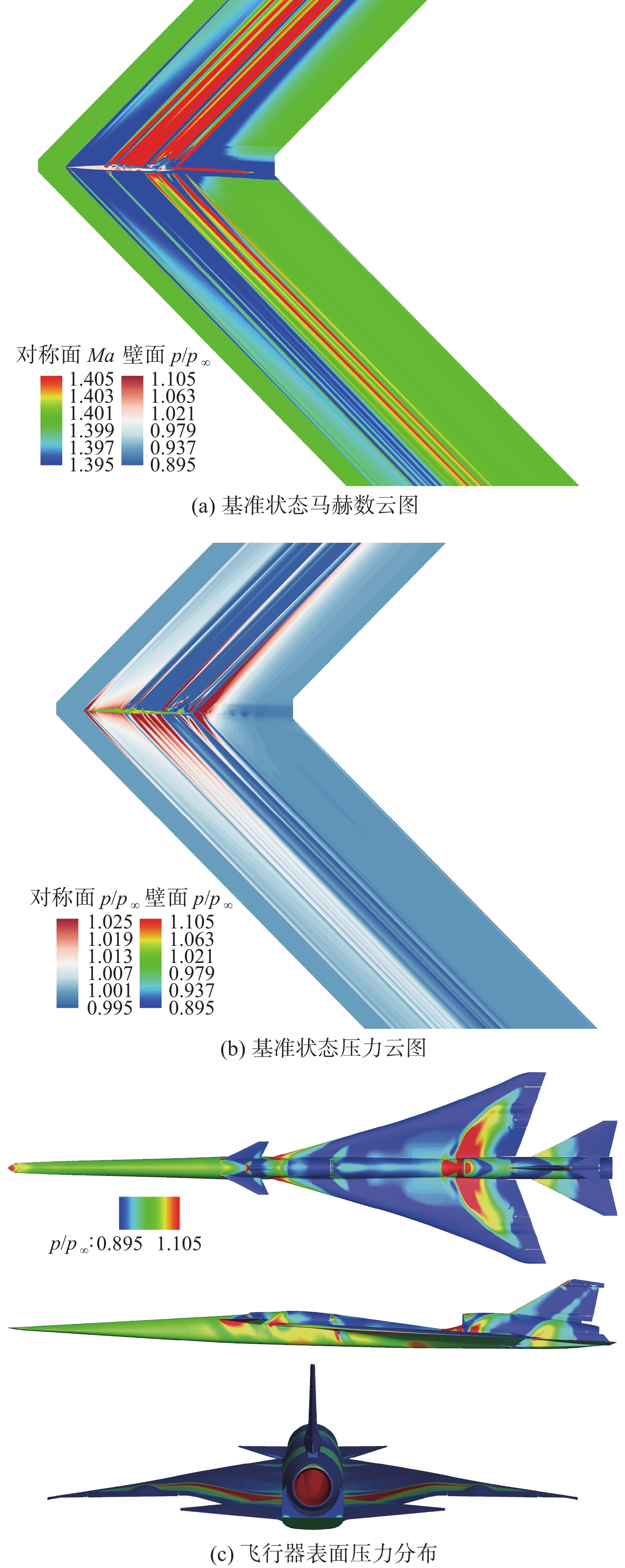
几何模型为C608飞行器,三维外形见图1,基准状态飞行条件如表1所示。CFD计算采用SA湍流模型,空间格式为二阶精度,时间推进方法为GMRES方法[29]。图4(a,b)给出了基准状态下马赫数和压力云图,图4(c)为飞行器表面压力分布图。机头产生激波和膨胀波对,在未受干扰前,细长的机身使流动平缓压缩。机翼前缘、舱盖后面的涡流发生器和ECS进气道产生了一系列快速变化的激波和膨胀波。入口溢出在机翼上形成一个高压区域。机翼后缘、水平尾翼、T型尾翼、发动机羽流等产生极其复杂的流动干扰,同时引发另一系列快速变化的激波和膨胀波。
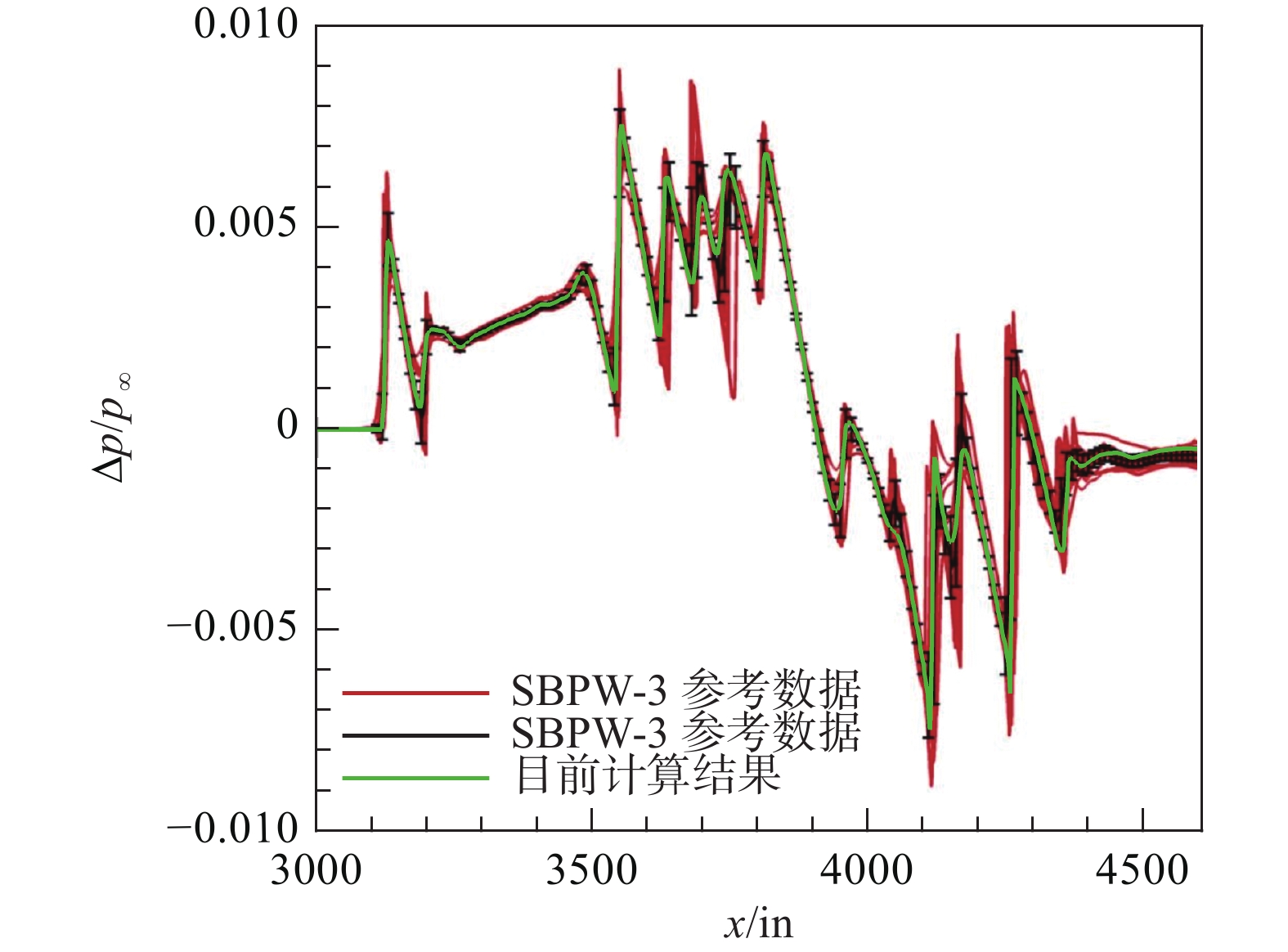
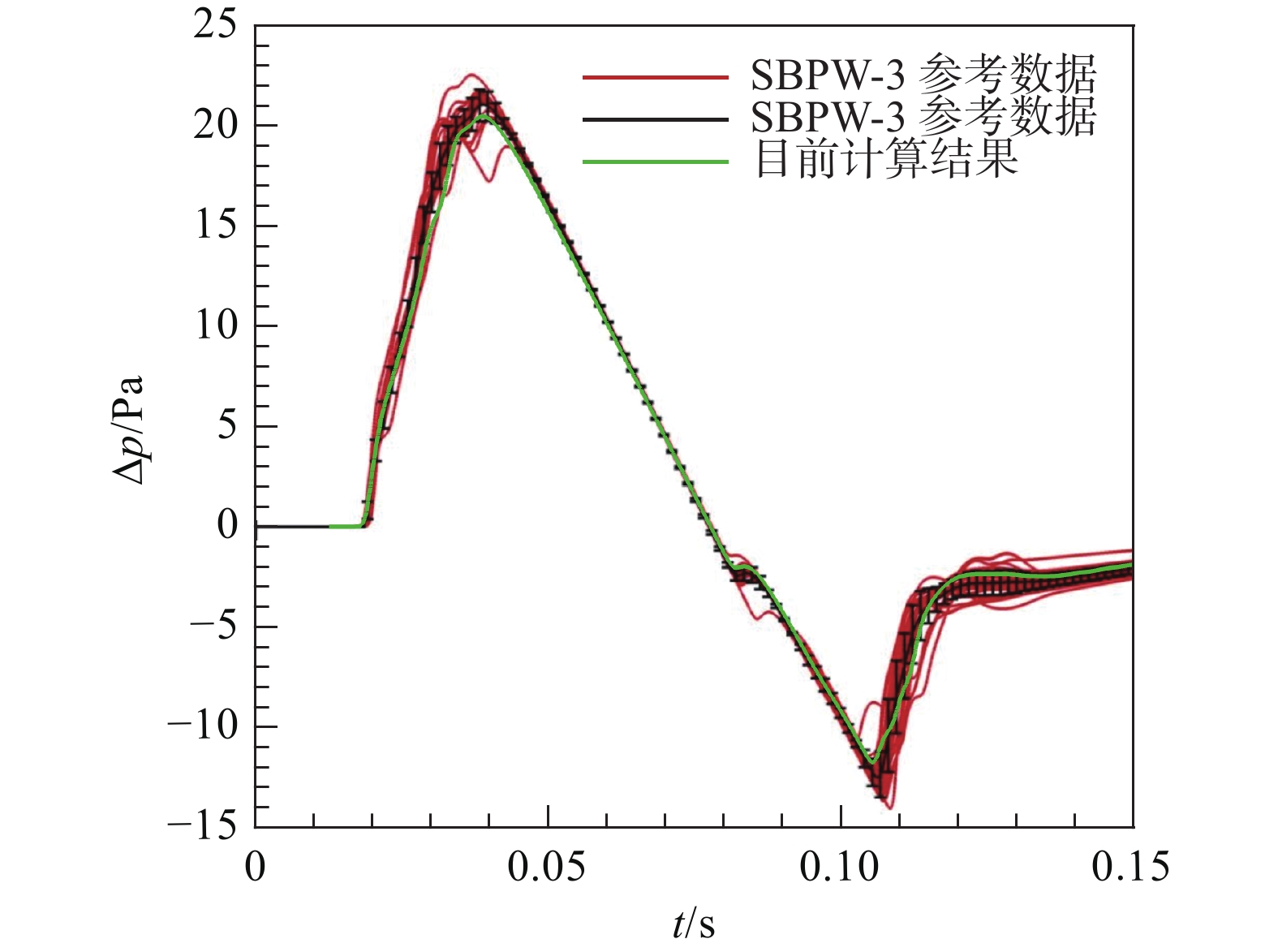
图5和图6分别对比了当前计算的近/远场波形与SBPW-3公布数据[8]的差异,其中红色和黑色线为SBPW-3数据,绿色实线为自研程序计算数据。可以发现,预测的近/远场波形与SBPW-3数据基本重合,说明自研CFD程序和声爆程序计算准确度符合要求,达到了较好的精度。整体近场过压值分布变化频率较高,存在多个波峰和波谷。由于经典吸收、分子弛豫效应等,使得大气具有类似低通滤波器的性质,声波能量及高频脉动在大气传播过程中被消耗成内能,因而远场地面波形较为平滑。
3.2 物理模型影响
本文选取层流模型、SA模型、SA-QCR模型[30]和SST模型来研究物理模型对近场过压值分布及远场地面波形的影响。
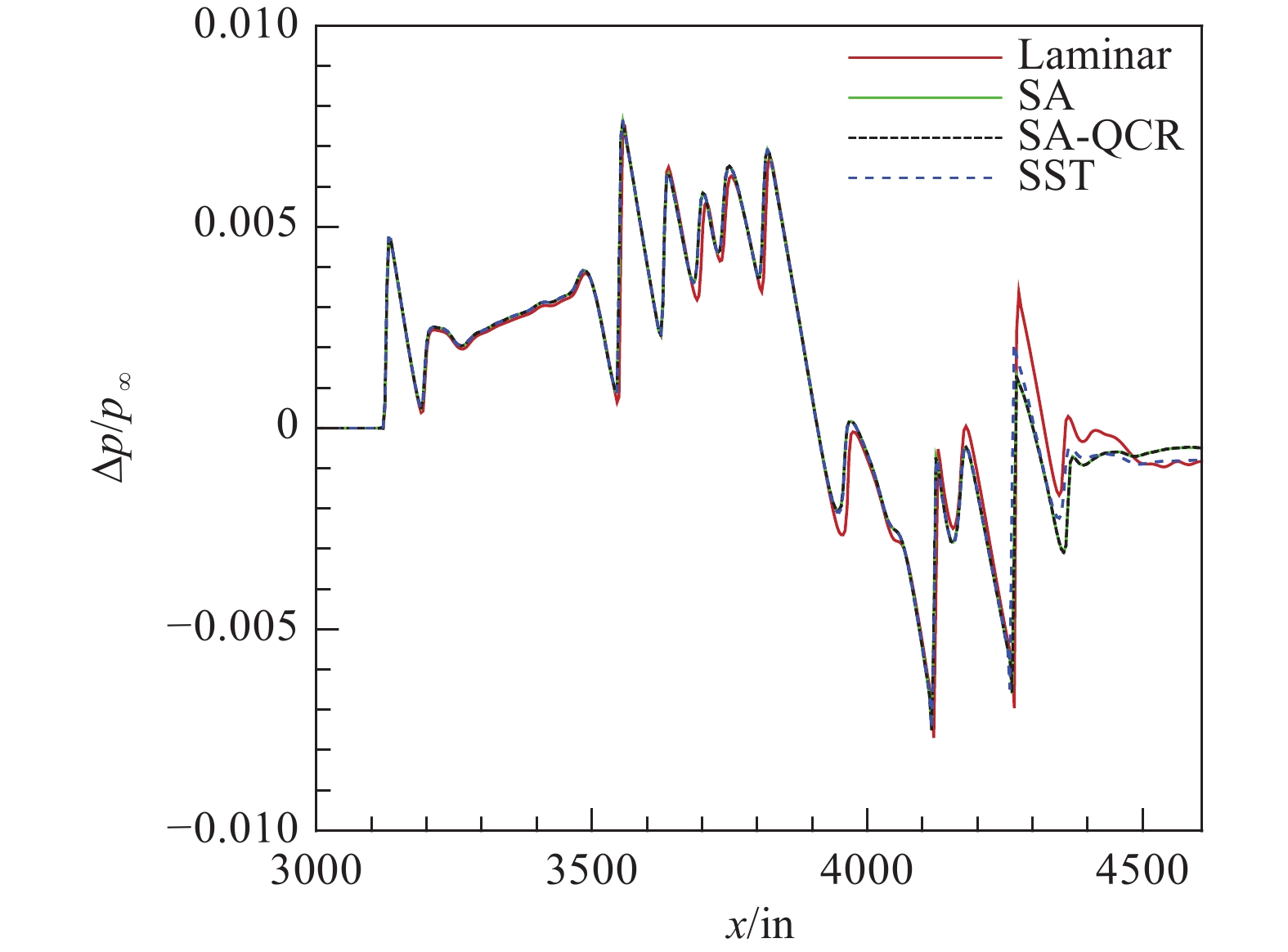
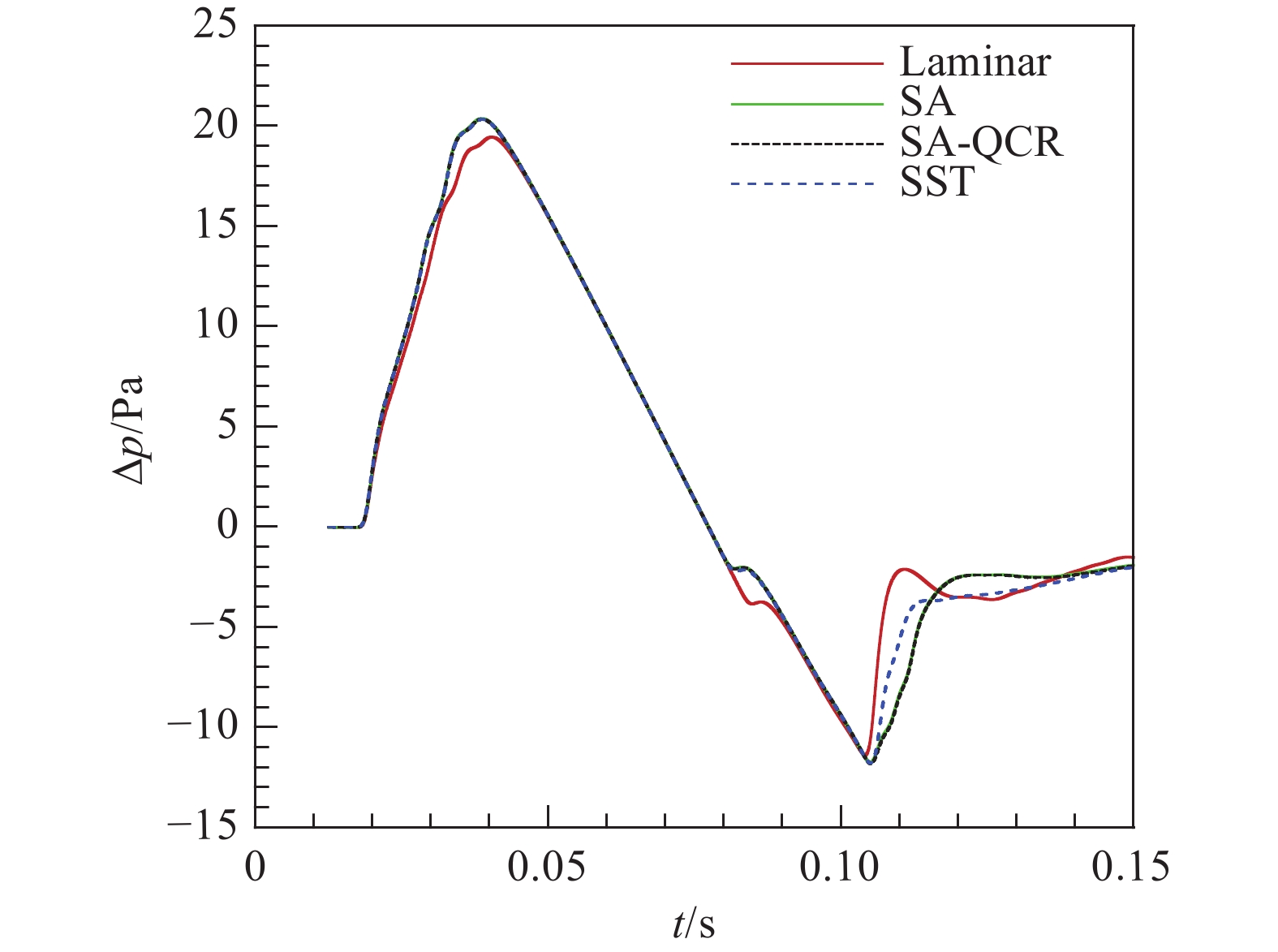
首先,给出层流模型下计算所得的马赫数和压力云图(见图7)。与SA湍流模型(见图4)相比,层流模型马赫数和压力云图在上下部分和飞行器前部与SA模型计算结果类似,在飞行器尾流部分两者相差较大,其主要原因在于尾部区域喷流与主流之间有较强的剪切、湍流掺混,该区域用层流模型是不合适的。
接着,图8和图9对比了不同物理模型下近场过压值分布和远场地面波形的差异。从图中可以看出:层流模型与湍流模型计算结果差别较明显(尤其尾部区域),同时层流模型对地面波形过压值预测偏低;SA湍流模型与SA-QCR湍流模型计算结果几乎重合;SST湍流模型与SA湍流模型,前部波形几乎一致,只有在尾部区域有较明显的差异。综合来看,不同湍流模型对近/远场波形的影响相对较小,层湍模型对近/远场波形的影响相对较大。
3.3 相对湿度影响
未来超声速客机飞行将跨越海洋和大陆,两者之间的相对湿度相差较大,而分子弛豫效应的强度与空气湿度极为相关,因此本节研究不同湿度对地面波形的影响。
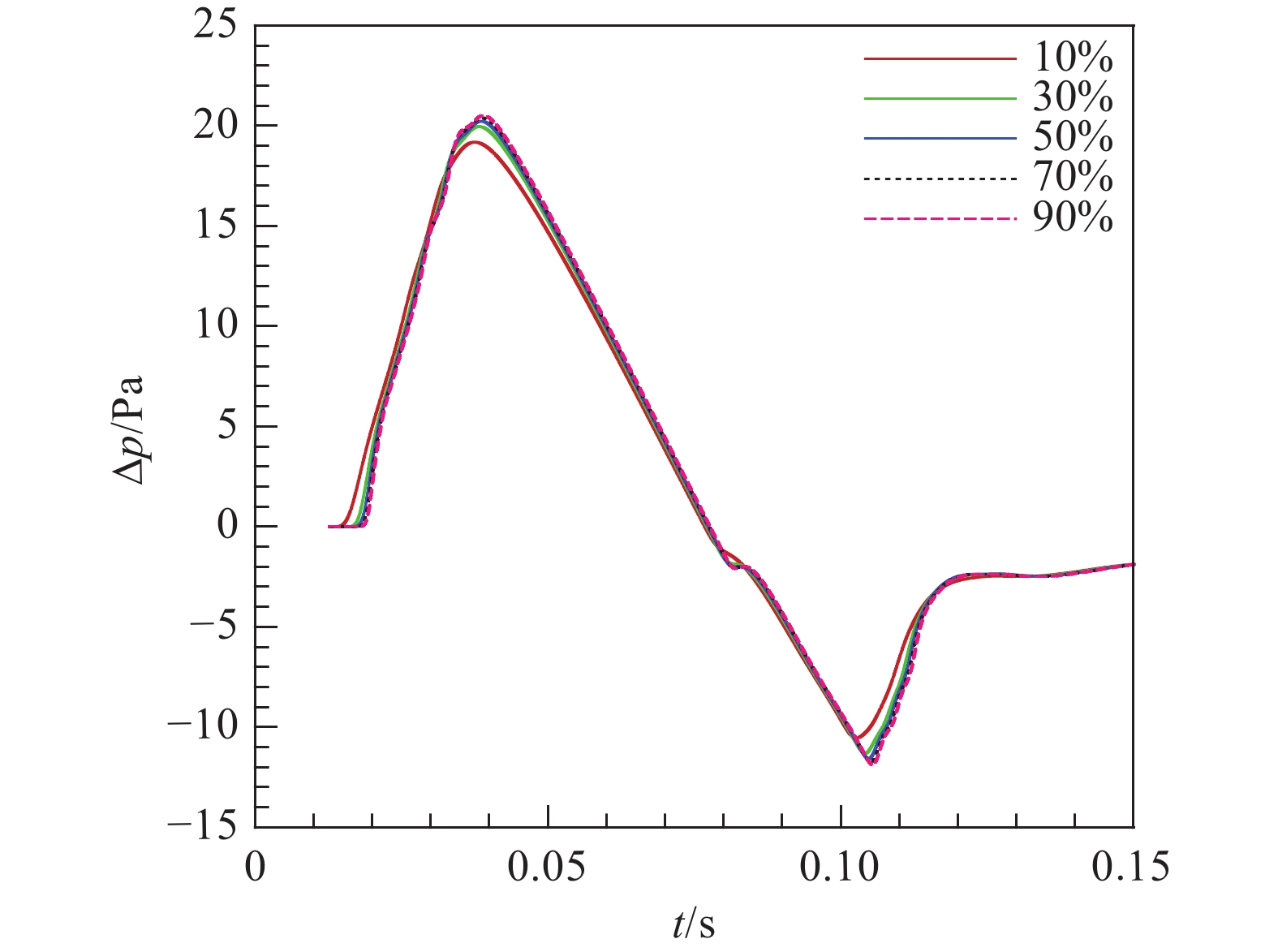
简单起见,考虑5个不同的相对湿度(10%、30%、50%、70%、90%)进行计算,其中10%相对湿度近似模拟沙漠等干旱地区湿度,90%相对湿度近似模拟沿海等湿润地区湿度。图10给出了在不同相对湿度的大气中的远场地面波形。可见,相对于高湿度,低湿度对波形幅值的影响较大。相对湿度越低的大气,其远场地面波形的过压值峰值更低,这是由于干燥的空气对于声波的耗散更强。文献[31]表明,对于声波在大气中的传播过程,因分子弛豫效应而产生的衰减,可以用一个衰减因子来衡量衰减的快慢,而声爆波形频率分量大多处于约化声波频率较低处,约化衰减因子会随相对湿度的减小而增大,因此干燥的空气对声爆波形的耗散作用更强。此外需要说明的是,除本小节外,本文其余计算均假定相对湿度为70%。
4. 不确定度量化分析
超声速客机在高空飞行过程中,来流条件会不断发生波动。因此需要考虑来流参数存在不确定性时对声爆预测结果的影响,并甄别来流参数中影响声爆预测的关键性因素,为超声速客机工程实际应用提供有价值的参考。本文选用C608低声爆超声速飞行器为研究对象,采用SA湍流模型和增广Burgers方程开展声爆近/远场信号不确定度量化分析。
4.1 样本点选取
超声速客机巡航飞行环境一般位于大气平流层,平流层中来流温度基本不变。本文选取三个来流参数变量(来流马赫数、来流攻角和单位雷诺数)作为随机不确定性输入参数,同时将地面波形过压值
\Delta p 作为输出响应,开展声爆近/远场波形的不确定传播和参数敏感性分析。三个变量的取值范围参考SBPW-3官网[7]和相关文献[8,17],并假设均服从均匀分布,不确定范围设置如表5所示。其中:来流马赫数基准值1.4,变化范围为±3%,对应参数变化范围为[1.358, 1.442];来流攻角基准值0°,参数变化范围为[−0.2°, 0.2°];单位雷诺数4321890 m−1,变化范围±10%,对应参数变化范围为[3889701 m−1, 4754079 m−1]。表 5 输入变量参数变化范围Table 5. Ranges of input variables参 数 参数变化范围 来流马赫数 [1.358, 1.442] 来流攻角/(°) [–0.2, 0.2] 来流单位雷诺数/(m-1) [3889701, 4754079] 点配置非嵌入式多项式混沌方法(NIPC)采用二阶截断,为了更高精度地计算混沌多项式的系数,采用两倍过采样样本。因此,本文利用拉丁超立方抽样方法抽取20个样本点。如图11所示,本文选取的样本点分布均匀。在每一个选取的样本点上开展确定性的近场CFD计算和远场增广Burgers方程计算。后续将根据样本点上的计算结果开展声爆近/远场信号不确定性量化分析。
4.2 近场波形不确定度量化分析
为了便于开展不确定度量化分析,将所有样本近场波形第一个波峰起点取为一致。图12给出所有样本点近场过压值分布。从中可以发现,在近场过压值的波峰、波谷等处存在较大的不确定度。
在95%置信区间内,声爆信号的不确定区间为
\left( {\mu - 1.96\sigma ,\mu + 1.96\sigma } \right) ,区间大小为2 \times 1.96\sigma ,其中\mu 为平均值,\sigma 为标准差。图13为NIPC方法计算的近场过压值均值与基准状态近场过压值。从图中可以看到,基准状态下的近场过压值和NIPC近场过压值均值基本一致,在波峰、波谷处有一定差异。4.3 远场波形不确定度量化分析
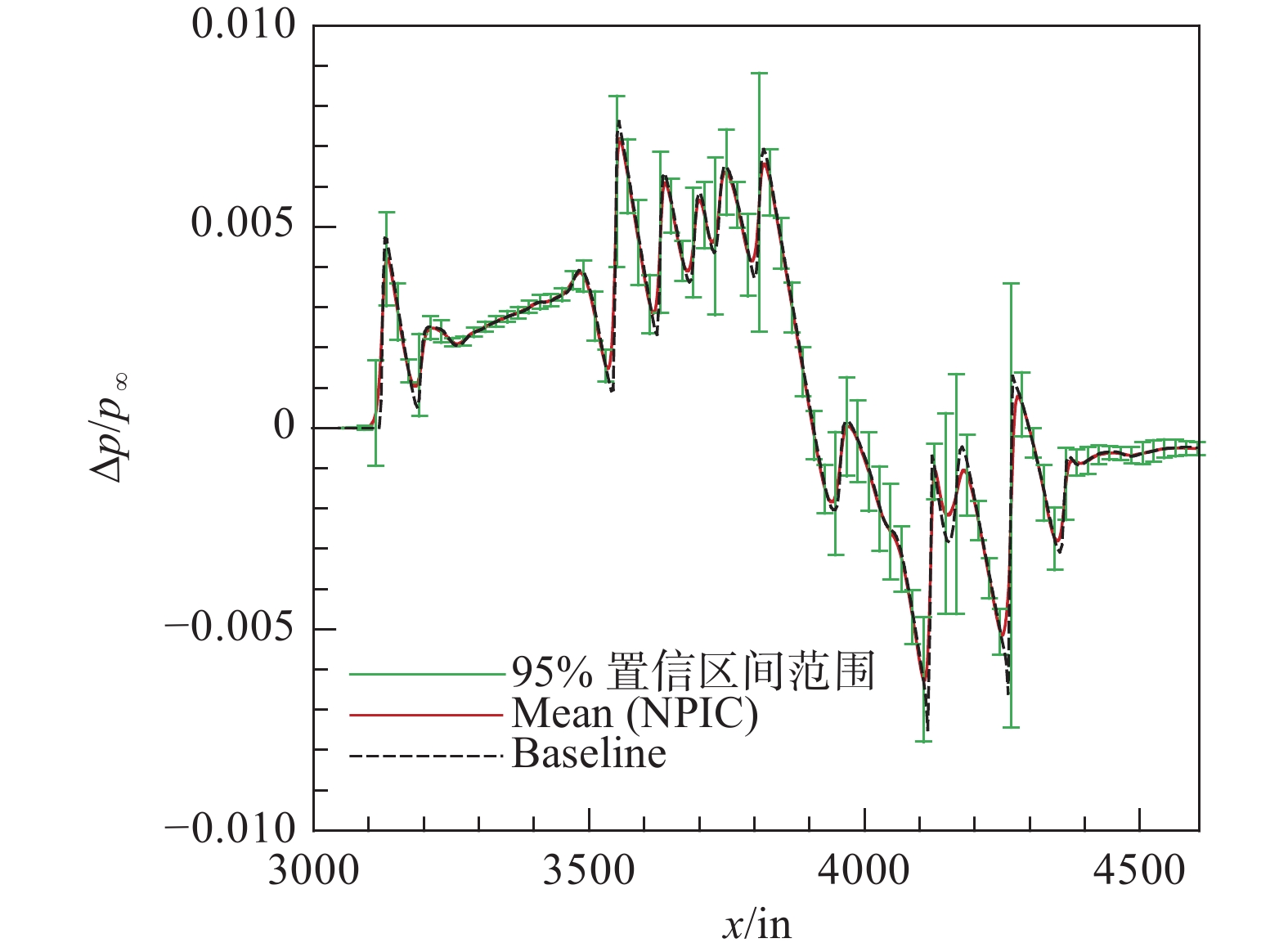
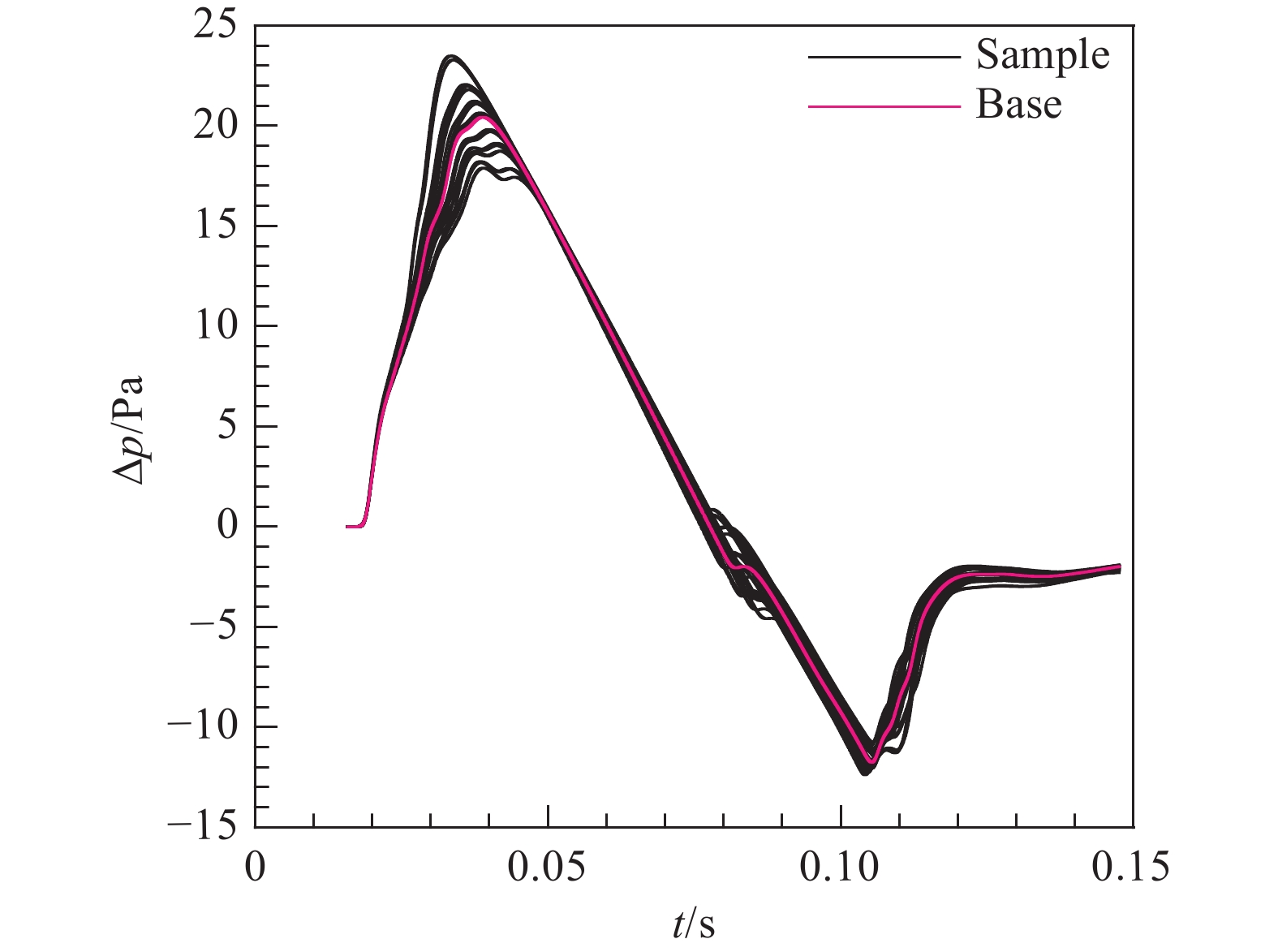
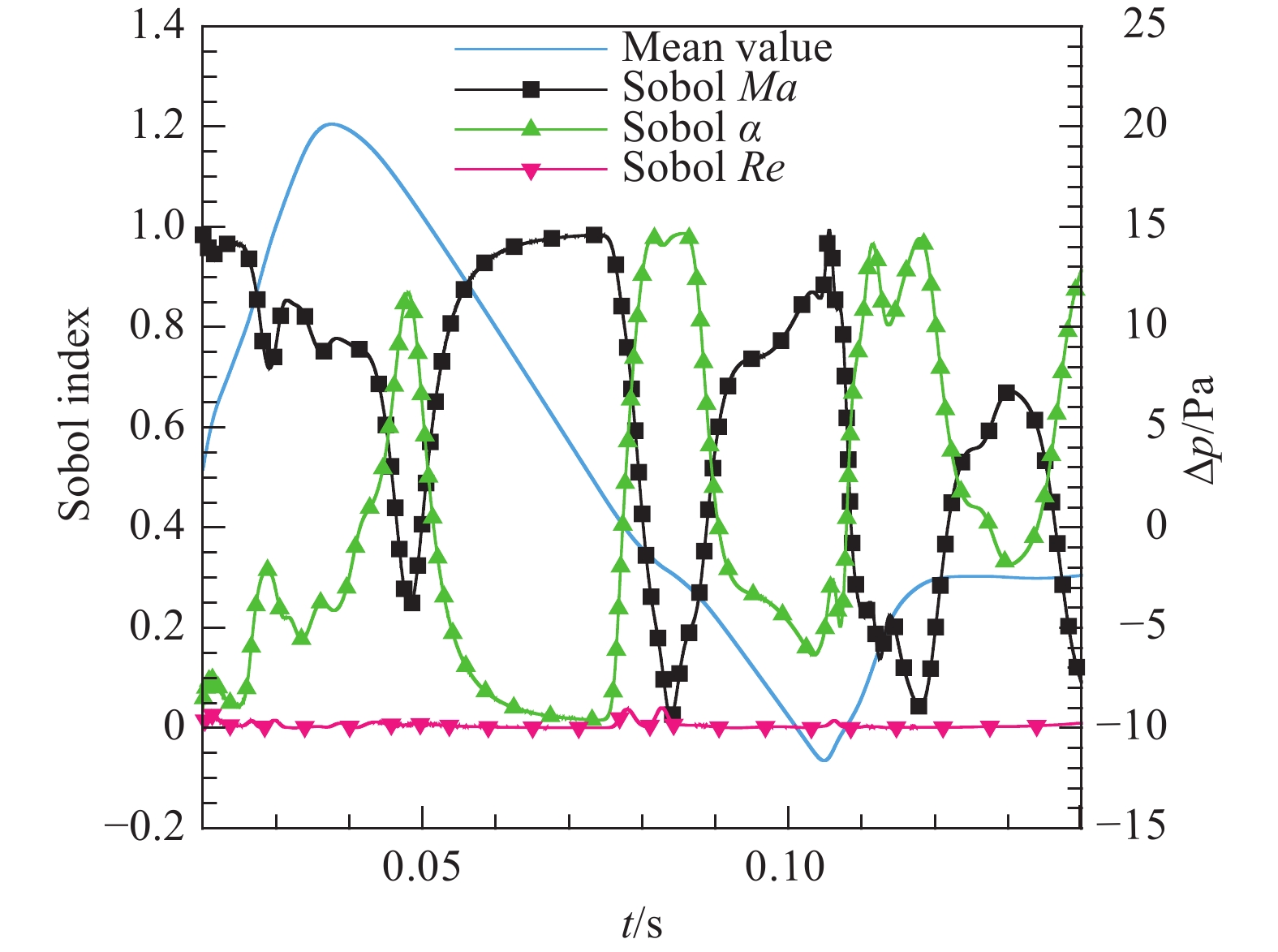
本文将所有样本远场地面波形起点取为一致,以便开展不确定度量化分析。图14给出所有样本点远场地面波形分布。可以发现,整体地面波形在第一波峰、中间转折及波谷处存在较大的不确定度。
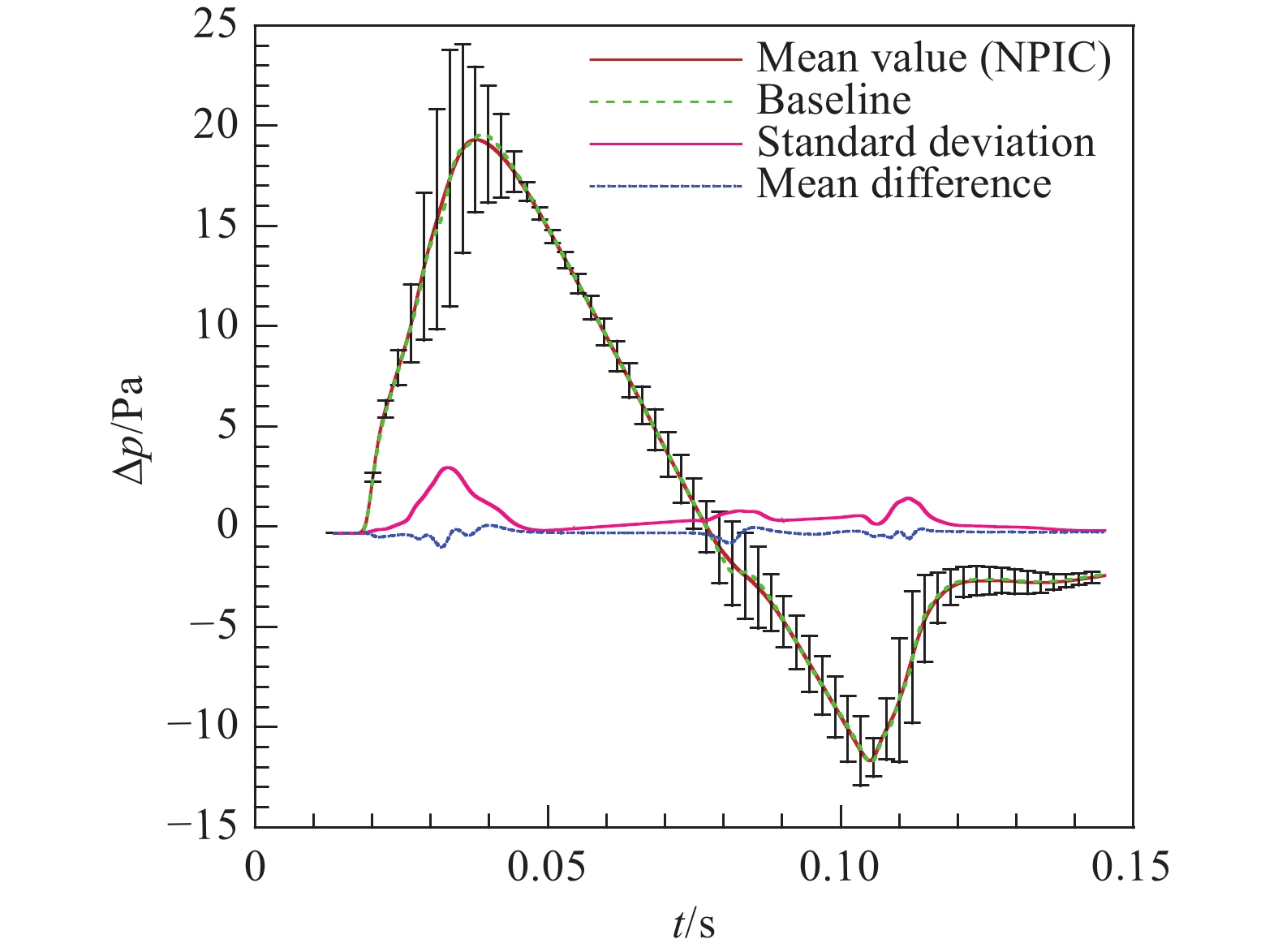
在95%置信区间内,定义输出地面波形的不确定度为
UQ = 1.96{{{\sigma _{_R}}} \mathord{\left/ {\vphantom {{{\sigma _{_R}}} {{\mu _{_R}}}}} \right. } {{\mu _{_R}}}} \times100\% 。图15为NIPC方法计算的地面波形均值和标准差,其中蓝色虚线为基准状态过压值与NIPC均值之差,粉红实线为NIPC均值的标准差。从图中可以看到,基准状态下的地面波形和NIPC地面波形均值基本一致,整体差别较小。此外,标准差在三个地方存在峰值,分别是t = 0.0327、t = 0.0837、t = 0.1113,对应标准差为3.3560、1.1184和1.8021。图16分别给出了不同来流参数的敏感性(Sobol)指数分布。通过前述三个来流参数不同时刻对应的敏感性指数分析,可以观察到来流参数对声爆传播的影响程度。由图16可知,来流单位雷诺数对地面波形过压值的影响显著低于来流马赫数和来流攻角的影响,后两者对地面波形不确定度贡献较大。从流动机理上来看,声爆近场及远场过压分布取决于脱体膨胀波和压缩波,其中来流马赫数和迎角对脱体空间波系结构特征影响较大,而雷诺数主要作用于物面附近,对脱体空间波系结构特征影响相对较小。
不确定度量化和敏感性分析表明,在低声爆超声速飞行器声爆传播预测数值模拟中,需要重点关注来流马赫数和来流攻角的变化。不确定性输入变量会引起远场地面波形、波峰与波谷处的过压值产生明显变化。来流马赫数变化(±3%)和来流攻角变化([−0.2°, 0.2°])对地面波形Sobol指数贡献最大的分别是t = 0.07414和t = 0.08584时刻,对应Sobol指数分别为0.9844和0.9868。
5. 结 论
本文对AIAA第三届声爆预测研讨会提供的C608低声爆超声速飞行器开展了声爆传播预测及不确定度量化分析,开展了远场地面信号空间维度和时间维度上的网格收敛性研究,并对比基准状态下不同湍流模型以及相对湿度对声爆预测的影响。此外,选取来流马赫数、来流攻角及来流单位雷诺数等三个不确定性输入变量,采用非嵌入式多项式混沌方法对声爆近/远场信号进行了不确定度量化分析和敏感性分析,得到的结论如下:
1) C608飞行器标准算例声爆近/远场波形与SBPW-3公布数据相吻合,表明自研CFD软件及声爆程序计算准确度符合要求,具有较好预测精度。
2) 层流模型相较于湍流模型,在飞行器尾流部分预测较差,同时对地面波形过压值预测偏低,不同湍流模型之间对声爆近/远场波形的影响较小。当相对湿度大于30%时,相对湿度对声爆近/远场波形的影响基本可以忽略不计。
3) 采用基于非嵌入式多项式混沌方法的不确定度量化分析方法,得到了近场波形均值、远场波形均值和标准差等。其中近/远场波形过压值均值与基准状态均值基本一致,仅在波峰和波谷处有一定差异。
4) 采用基于Sobol指数的敏感性方法,对地面波形过压值
\Delta p 进行了敏感性分析。其中来流单位雷诺数对地面波形过压值的影响显著低于来流马赫数和来流攻角的影响。此外,声爆地面感觉噪声级是对不同频率噪声强度的量化,与远场过压分布之间呈非线性关系,今后应开展基于感觉噪声级的不确定度分析。5) 来流条件的波动影响声爆近/远场信号,其中气流变化频率或飞行器运动频率对声爆信号传播产生复杂影响,如超声速加速飞行发生声爆聚集现象[32],有待开展深入研究。
-
表 1 C608来流和边界条件
Table 1 Freestream and boundary conditions of C608
参 数 量 值 来流马赫数 1.4 来流攻角/(°) 0 来流温度/K 216.61 飞行高度/m 16215.36 单位雷诺数/(m–1) 4321890 发动机喷嘴增压室总压与来流静压之比 10.0 发动机喷嘴增压室总温与来流静温之比 7.0 发动机旁路排气总压与来流静压之比 2.4 发动机旁路排气总温与来流静温之比 2.0 发动机风扇表面静压与来流静压之比 2.6 环境控制系统入口静压与来流静压之比 1.4 表 2 非结构混合网格
Table 2 Unstructured hybrid grid
网格名称 特征网格尺度 节点数 单元数 四面体 棱柱 Mix-064 0.58 50215130 36567810 86083502 表 3 不同空间网格密度
Table 3 Different spatial grid sizes
算例 空间网格点数 时间网格点数 采样率/kHz 1 2500 50000 335.94 2 5000 50000 335.94 3 10000 50000 335.94 4 20000 50000 335.94 5 40000 50000 335.94 表 4 不同时间网格密度
Table 4 Different temporal grid sizes
算例 空间网格点数 时间网格点数 采样率/kHz 1 20000 5000 33.59 2 20000 10000 67.19 3 20000 30000 201.56 4 20000 50000 335.94 5 20000 70000 470.32 表 5 输入变量参数变化范围
Table 5 Ranges of input variables
参 数 参数变化范围 来流马赫数 [1.358, 1.442] 来流攻角/(°) [–0.2, 0.2] 来流单位雷诺数/(m-1) [3889701, 4754079] -
[1] WHITHAM G B. The flow pattern of a supersonic projectile[J]. Communications on Pure and Applied Mathematics, 2006, 5(3): 301-348. DOI: 10.1002/cpa.3160050305
[2] SEEBASS A R. Sonic boom research[R]. NASA SP147. Washington, Dc: NASA, 1967.
[3] SCHWARTZ I R. Second conference on sonic boom research[R]. NASA SP-180. Washington, DC: NASA, 1968.
[4] SCHWARTZ I R. Third conference on sonic boom research[R]. NASA SP-255. Washington, DC: NASA, 1970.
[5] 1st Workshop (2014) | ASA 2022 special focus boom session[EB/OL]. https://lbpw.larc.nasa.gov/sbpw1/ , (2019-03-07), [2021-07-30].
[6] 2nd Workshop (2017) | ASA 2022 special focus boom session[EB/OL]. https://lbpw.larc.nasa.gov/sbpw2/ , (2019-03-07), [2021-07-30].
[7] 3rd Workshop (2020) | ASA 2022 special focus boom session[EB/OL]. https://lbpw.larc.nasa.gov/sbpw3/ , (2020-07-25), [2021-07-30].
[8] PARK M A, CARTER M B. Nearfield summary and analysis of the third AIAA sonic boom prediction workshop C608 low boom demonstrator[C]//AIAA Scitech 2021 Forum, . Reston, Virginia: AIAA, 2021. AIAA 2021-0345.doi: 10.2514/6.2021-0345
[9] PLOTKIN, KENNETH J. State of the art of sonic boom modeling[J]. Journal of the Acoustical Society of America, 2002, 111(1): 530-536. DOI: 10.1121/1.1379075
[10] POTAPKIN A, KOROTAEVA T, MOSKVICHEV D, et al. An advanced approach for far-field sonic boom prediction[C]//47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, Florida. Reston, Virigina: AIAA, 2009. doi: 10.2514/6.2009-1056
[11] PLOTKIN K. Review of sonic boom theory[C]//12th Aeroacoustic Conference, San Antonio, TX, USA. Reston, Virigina: AIAA, 1989. doi: 10.2514/6.1989-1105
[12] RALLABHANDI S. Advanced sonic boom prediction using augmented burger’s equation[C]//49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, Florida. Reston, Virigina: AIAA, 2011. doi: 10.2514/6.2011-1278
[13] YAMASHITA R, SUZUKI K. Full-field sonic boom simulation in stratified atmosphere[J]. AIAA Journal, 2016, 54(10): 3223-3231. DOI: 10.2514/1.J054581
[14] 朱自强, 兰世隆. 超声速民机和降低音爆研究[J]. 航空学报, 2015, 36(8): 2507-2528. doi: 10.7527/S1000-6893.2014.0207 ZHU Z Q, LAN S L. Study of supersonic commercial transport and reduction of sonic boom[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(8): 2507-2528. (in Chinese) doi: 10.7527/S1000-6893.2014.0207
[15] 张绎典, 黄江涛, 高正红. 基于增广Burgers方程的音爆远场计算及应用[J]. 航空学报, 2018, 39(7): 96-107. doi: 10.7527/S1000-6893.2018.22039 ZHANG Y D, HUANG J T, GAO Z H. Far field simulation and applications of sonic boom based on augmented Burgers equation[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(7): 96-107. (in Chinese) doi: 10.7527/S1000-6893.2018.22039
[16] HOSDER S, WALTERS R, PEREZ R. A non-intrusive polynomial chaos method for uncertainty propagation in CFD simulations[C]//44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virginia: AIAA, 2006: 891. doi: 10.2514/6.2006-891
[17] CARPENTER F L, CIZMAS P. UNS3D simulations for the third sonic boom prediction workshop part II: C608 low-boom flight demonstrator[C]//AIAA Aviation 2020 Forum, Virtual Event. Reston, Virginia: AIAA, 2020. doi: 10.2514/6.2020-2733
[18] 阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2006: 17-18. YAN C. Computational fluid dynamic's methods and applications[M]. Beijing: Beijing University of Aeronautics & Astronautics Press, 2006: 17-18 (in Chinese).
[19] BLACKSTOCK, DAVID T. Thermoviscous attenuation of plane, periodic, finite-amplitude sound waves[J]. Journal of the Acoustical Society of America, 1964, 36(3): 534-542. DOI: 10.1121/1.1918996
[20] PIERCE A D, BEYER R T. Acoustics: an introduction to its physical principles and applications. 1989 edition[J]. The Journal of the Acoustical Society of America, 1990, 87(4): 1826-1827. DOI: 10.1121/1.399390
[21] CLEVELAND R O. Propagation of sonic booms through a real, stratified atmosphere[D]. The University of Texas at Austin, 1995.
[22] PLOTKIN K, MAGLIERI D J. Sonic boom research: history and future[C]//33rd AIAA Fluid Dynamics Conference and Exhibit, Orlando, Florida. Reston, Virginia: AIAA, 2003. doi: 10.2514/6.2003-3575
[23] 熊芬芬, 杨树兴, 刘宇, 等. 工程概率不确定性分析方法[M]. 北京: 科学出版社, 2015: 115-117, 121-166. XIONG F F, YANG S X, LIU Y, et al. Engineering probability uncertainty analysis method[M]. Beijing: Science Press, 2015: 115-117, 121-166 (in Chinese).
[24] HOSDER S, WALTERS R W, BALCH M. Efficient sampling for non-intrusive polynomial chaos applications with multiple uncertain input variables[C]//48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, Hawaii. Reston, Virginia: AIAA, 2007. doi: 10.2514/6.2007-1939
[25] SCHAEFER J A, WEST T, HOSDER S, et al. Uncertainty quantification of turbulence model closure coefficients for transonic wall-bounded flows[C]//22nd AIAA Computational Fluid Dynamics Conference, Dallas, TX. Reston, Virginia: AIAA, 2015. doi: 10.2514/6.2015-2461
[26] 胡军, 张树道. 基于多项式混沌的全局敏感度分析[J]. 计算物理, 2016, 33(1): 1-14. doi: 10.3969/j.issn.1001-246X.2016.01.001 HU J, ZHANG S D. Global sensitivity analysis based on polynomial chaos[J]. Chinese Journal of Computational Physics, 2016, 33(1): 1-14. (in Chinese) doi: 10.3969/j.issn.1001-246X.2016.01.001
[27] Chao Pang, Zheng Hong GAO, Hua YANG, et al. An efficient grid assembling method in unsteady dynamic motion simulation using overset grid[J]. Aerospace Science and Technology, 2021, 110: 106450. DOI: 10.1016/j.ast.2020.106450
[28] Shusheng CHEN, Fangjie CAI, Xinghao XIANG, et al. A low-diffusion robust flux splitting scheme towards wide-ranging Mach number flows[J]. Chinese Journal of Aeronautics, 2021, 34(5): 628-641. DOI: 10.1016/j.cja.2020.12.010
[29] SAAD Y, SCHULTZ M H. GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems[J]. SIAM Journal on Scientific and Statistical Computing, 1986, 7(3): 856-869. DOI: 10.1137/0907058
[30] RUMSEY C L, CARLSON J R, PULLIAM T H, et al. Improvements to the quadratic constitutive relation based on NASA juncture flow data[J]. AIAA Journal, 2020, 58(10): 4374-4384. DOI:10.2514/1.J059683
[31] Bass H E, Sutherland L C, Zuckerwar A J, et al. Atmospheric absorption of sound: further developments[J]. The Journal of the Acoustical Society of America, 1995, 97(1): 680-683. DOI: 10.1121/1.412989
[32] SALAMONE J A , SPARROW V W, PLOTKIN K J. Solution of the lossy nonlinear tricomi equation applied to sonic boom focusing [J]. AIAA Journal, 2013, 51(7): 1745-1754. doi:10.2514/1.J052171
-
期刊类型引用(2)
1. 范杰,韩忠华,乔建领,陈晴,杨瀚,宋文萍. 超声速民机机动飞行的聚焦声爆全场预测方法研究. 宇航学报. 2024(10): 1538-1551 .  百度学术
百度学术
2. 冷岩,张劲柏,钱战森. 飞机超声速机动飞行条件声爆预测方法. 空气动力学学报. 2023(06): 45-54 .  本站查看
本站查看
其他类型引用(1)




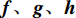
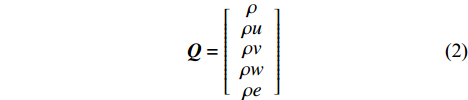
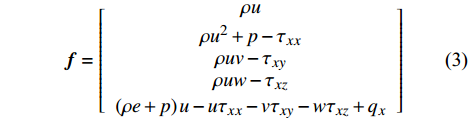
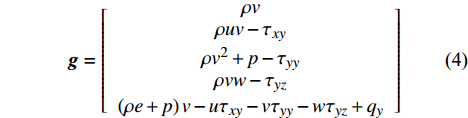
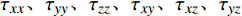
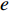
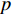
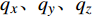
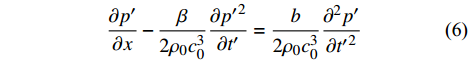
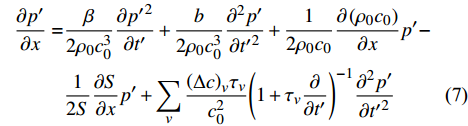
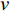
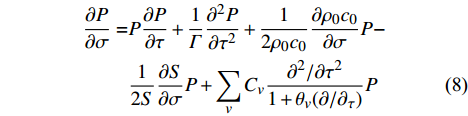
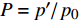
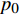
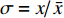
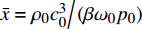
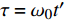
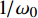
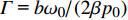
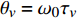
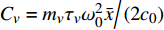
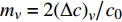
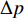
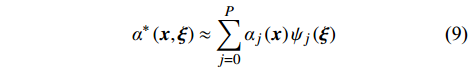
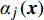
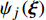
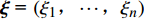
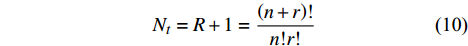
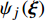
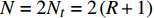
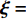
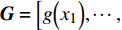
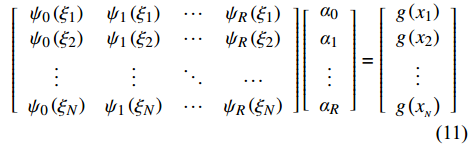
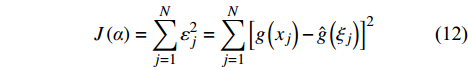
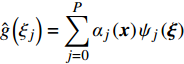
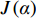
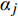

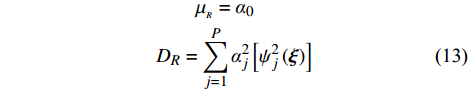
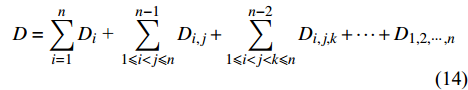
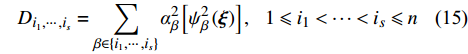
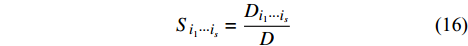
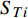
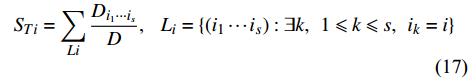

 下载:
下载: