0.   引　言

空泡与自由液面之间的相互作用是空泡动力学的经典课题之一，最早应用于研究水下爆炸，主要关注的是空泡非球形溃灭行为^[1-8]。无量纲距离参数$\gamma$定义为空泡中心距离自由面之间的距离$h$和其在无限水域振荡的最大半径${R}_{\mathrm{m}\mathrm{a}\mathrm{x}}$的比值，是影响空泡与自由液面相互作用的最重要参数。随着$\gamma$逐渐减小，空泡溃灭诱导的自由面变形主要表现为丘型、冲天型、皇冠型、溅射型、破碎型等^[9-10]。前四种形式中，自由面与空泡通常不会发生界面的直接相互作用，表现为以界面间液态水为间接媒介的弱耦合作用。当空泡和自由面距离近的情况下的破碎型行为演化更为复杂，空泡膨胀诱导自由面向上飞溅形成透明水层，二者界面交迭形成气流热量和质量交换的通路。与此同时，通路内高压气体排出，压力逐渐下降，外部气流沿通路侵入，导致通路内部的压力剧烈变化，驱动水层产生闭合等复杂行为。因此，空泡与自由面强耦合作用特点主要体现在空泡通气、自由面飞溅及闭合等行为。

近年来，强耦合作用下自由面大变形与飞溅水层演化的研究也得到更多关注。Wang^[11]发现，空泡通气过程是由于空泡壁面发生了Rayleigh-Taylor不稳定，并根据飞溅水层是否闭合给出了两种流态分类，与实验结果吻合较好。Li^[12]采用实验和仿真方法研究了空泡与自由面相互作用，并给出了三种空泡破碎形态。Tian^[13]基于欧拉有限元方法和流体体积法（volume of fluid, VOF）探究了近自由面空泡的通气和飞溅水层闭合过程，发现飞溅水层闭合后产生的向上的射流比空泡不破裂时产生的自由面射流演化更高。Rosselló^[14]采用伯努利方程建立模型模拟了飞溅水层闭合过程，将空泡膨胀过程视为圆柱形活塞入水过程，通过空泡膨胀速度间接得到空泡内与外界压强差，发现飞溅水层闭合主要是由于空腔内外压差导致的，表面张力对飞溅水层演化过程的影响是可以忽略的，他们还给出了空泡在$\mathrm{\gamma }$ = 0.075～0.25之间会产生“子弹”状射流。Marston^[15]实验研究了不同环境压力的飞溅水层演化，指出空泡的快速膨胀所产生的吸力是导致飞溅水层闭合的原因。基于上述研究，空泡破碎与通气、自由面飞溅与闭合等过程具有强非线性、非定常等特点。

空泡诱导自由面液面飞溅与闭合现象，与结构物入水^[16-18]产生的表面闭合现象十分相似。Aristoff^[19]发现，低邦德数（Bond number）下小球入水产生的空腔的溃灭过程主要是由于表面张力驱动的，并提出了高邦德数下耦合空腔动力学的飞溅水层演化的理论模型。Eshraghi^[20]基于实验与理论方法，提出了一套描述飞溅水层轨迹的物理模型，探究了水层内外压差、表面张力与重力等对水层闭合的影响。Wang^[21]通过理论与实验方法对入水过程的表面闭合机制进行了研究，讨论了重力、阻力、表面张力与空气动压对表面闭合水层的影响，发现空气动压主导了飞溅水层的表面闭合过程。上述入水诱导的飞溅水层建模方法、闭合机制讨论及主控参数影响规律等研究过程，对本文空泡和自由面之间强耦合作用下自由面飞溅闭合过程的水层建模、受力分析、主控参数确定提供了重要参考。

以上主要通过定性实验观测解释了飞溅水层闭合过程，对于其主要控制参数缺少定量测量，本文基于数值模拟获得的飞溅水层围成的通路内的速度场和压力场信息，直接提取外部气体侵入空泡内部导致的压强差变化，并对水层受力进行分析，直接计算了各项作用力随时间的演化，定量揭示了空泡与自由面强耦合作用诱导的水层闭合机制，并获得了水层闭合时间与环境压力的幂次律关系。

1.   数值模拟方法

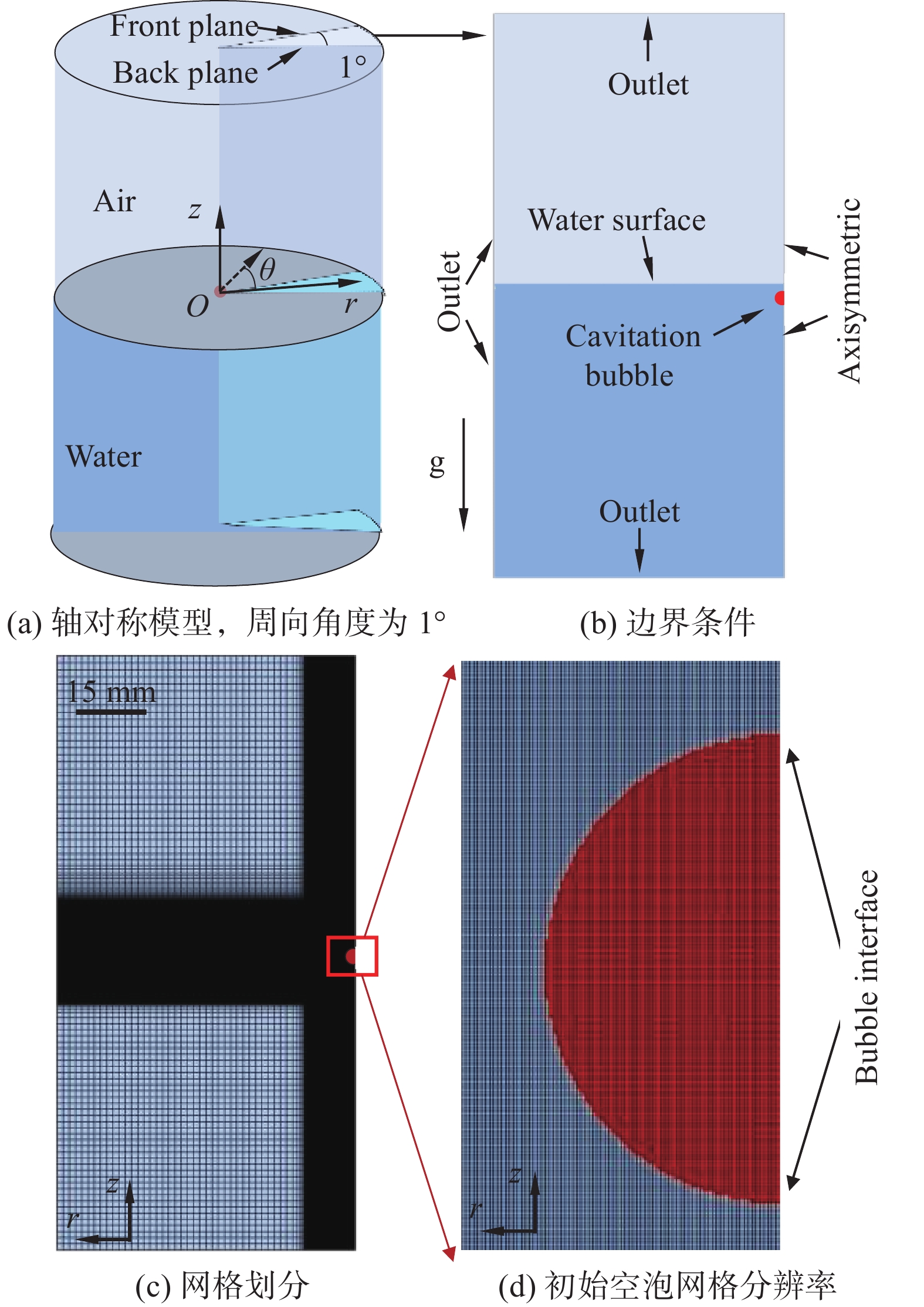
本文的数值模拟参考Zeng^[22] 和 Wang^[23-24]对液滴内空泡动力学行为的研究，空泡初始化为一个振荡的空化泡。轴对称模型如图1（a）所示，模型中采用柱坐标系$O-r\theta z$ 表达，原点O位于初始空泡中心，r轴沿着径向方向，向外侧为正，z轴代表轴向方向，向上为正。计算域长为60 mm、高为120 mm。边界条件如图1（b）所示，最右侧为轴对称边界，其他为出口边界。网格划分如图1（c）所示，采用正交笛卡尔网格进行划分。对空泡和自由面附近进行局部加密，初始空泡在径向方向包含60个网格，局部加密区域网格尺寸为5 μm，总网格量为384万。

图  1  计算模型

Figure  1.  Computational modelling

下载: 全尺寸图片 幻灯片

本文基于OpenFOAM平台，采用有限体积法直接求解N-S方程，并采用VOF来捕捉气液界面^[25-27]。基于压力-隐式分裂算子（pressure-implicit with splitting of operators， PISO） 的多相可压缩求解器（compressibleInterFoam） 模拟空泡和自由面之间的强耦合作用。气体与液体均视为牛顿流体，连续性方程、动量方程、能量方程与输运方程是：

式中：$\boldsymbol \nabla$为梯度算子；$t$是时间；$\boldsymbol U$是速度矢量；${\boldsymbol{U}}_{\mathit{r}}$是气液界面相对速度；$p$是压力；${\rho }_{{\rm{m}}}$是混合物密度，${\rho }_{{\rm{m}}}= {\rho }_{{\rm{l}}}\alpha +{\rho }_{\text{g}}\left(1-\alpha \right)$；${\rho }_{{\rm{l}}}$和${\rho }_{\text{g}}$分别是液体和气体的密度；$\alpha$是体积分数；g是重力加速度；$\sigma$是表面张力系数；${\mu }_{{\rm{m}}}$是混合动力学黏度，${\mu }_{{\rm{m}}}={\mu }_{{\rm{l}}}\alpha +{\mu }_{\text{g}}(1-\alpha )$；${\mu }_{{\rm{l}}}$和${\mu }_{\text{g}}$分别为液体和气体的动力学黏度；$\kappa$是气-液界面曲率，$\kappa= \mathrm{\boldsymbol{\nabla}}\cdot\mathbf{n}$；$T$为温度；${C}_{v}={C}_{v{\rm{l}}}\alpha +{C}_{v{\rm{g}}}(1-\alpha )$，${C}_{v{\rm{l}}}$和${C}_{v{\rm{g}}}$分别为液体和气体的比热容；$\lambda$为热传导系数；$k$为单位质量的动能。

考虑到空泡和外界空气发生连通，空泡内气体和外界大气之间会发生热交换等，仿真中气体和液体分别采用perfectGas 和perfectFluid状态方程^{[23, 28]}进行建模，如式（5、6）所示：

式中$：R$为状态参数，${\rho }_{{\rm{l}}0}$为$T=0$时液体的密度。本文采用隐式欧拉格式和二阶Gauss vanLeer格式来离散时间项和对流项。

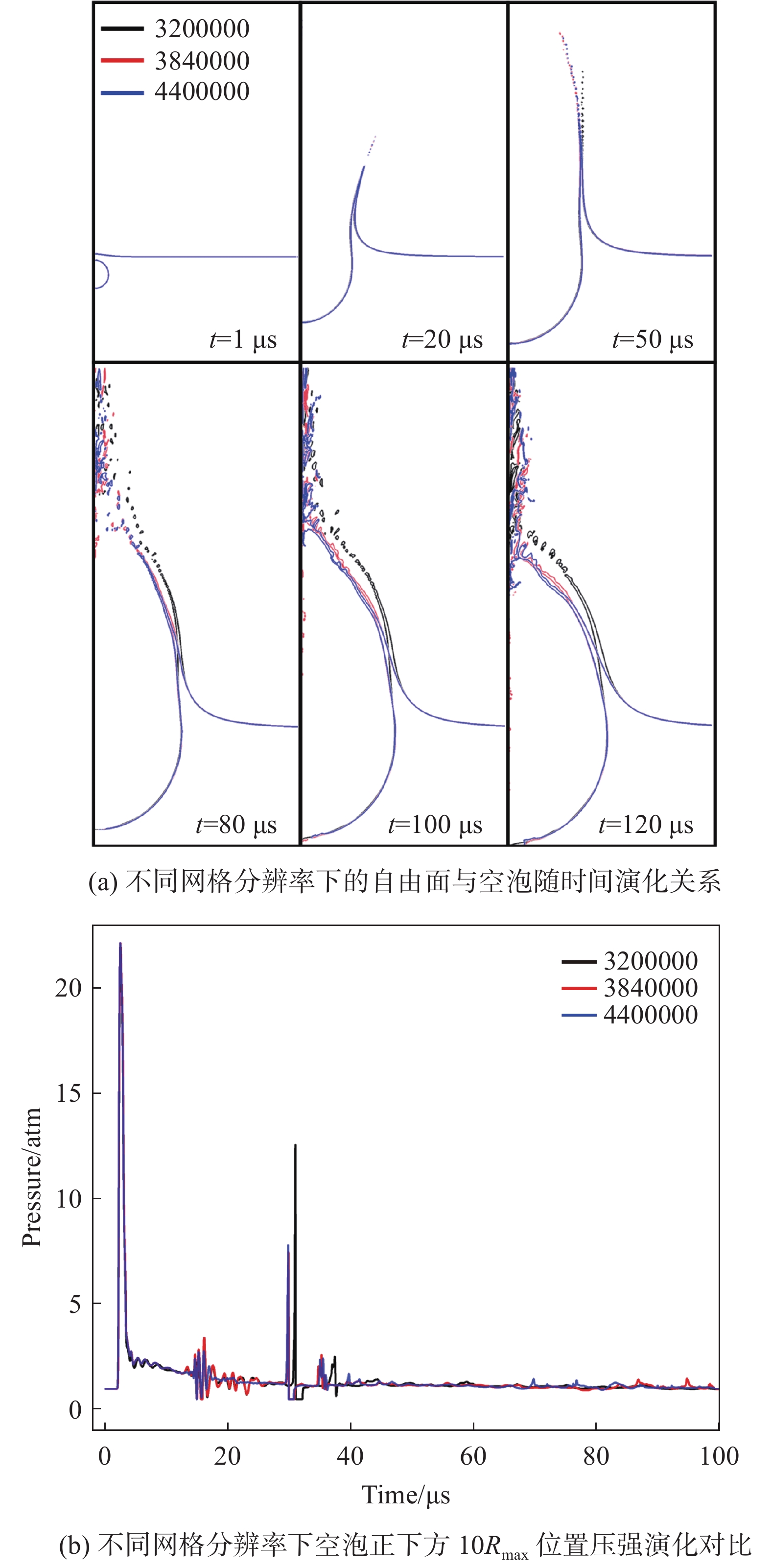
图2（a）展示的是不同网格分辨率下自由面飞溅与空泡随时间的演化过程，其中粗、中及细网格分别对应网格总量为320万、384万、440万。从对比结果可以看出，3种网格下的空泡轮廓基本吻合。对于飞溅水层模拟，中网格与细网格的结果基本吻合，粗网格结果与二者存在少许差异。图2（b）展示的是3种网格下空泡正下方10${R}_{\mathrm{m}\mathrm{a}\mathrm{x}}$处的压强演化对比。从对比结果可知，中网格与细网格结果吻合较好，粗网格的结果在第二次反射的压力值稍高于前两者。考虑到计算资源与计算精度的平衡，本文采用中网格来探究空泡和自由面之间的强耦合作用。

图  2  网格无关性验证

Figure  2.  Grid independence verification

下载: 全尺寸图片 幻灯片

2.   结果与讨论

2.1   数值模拟方法验证

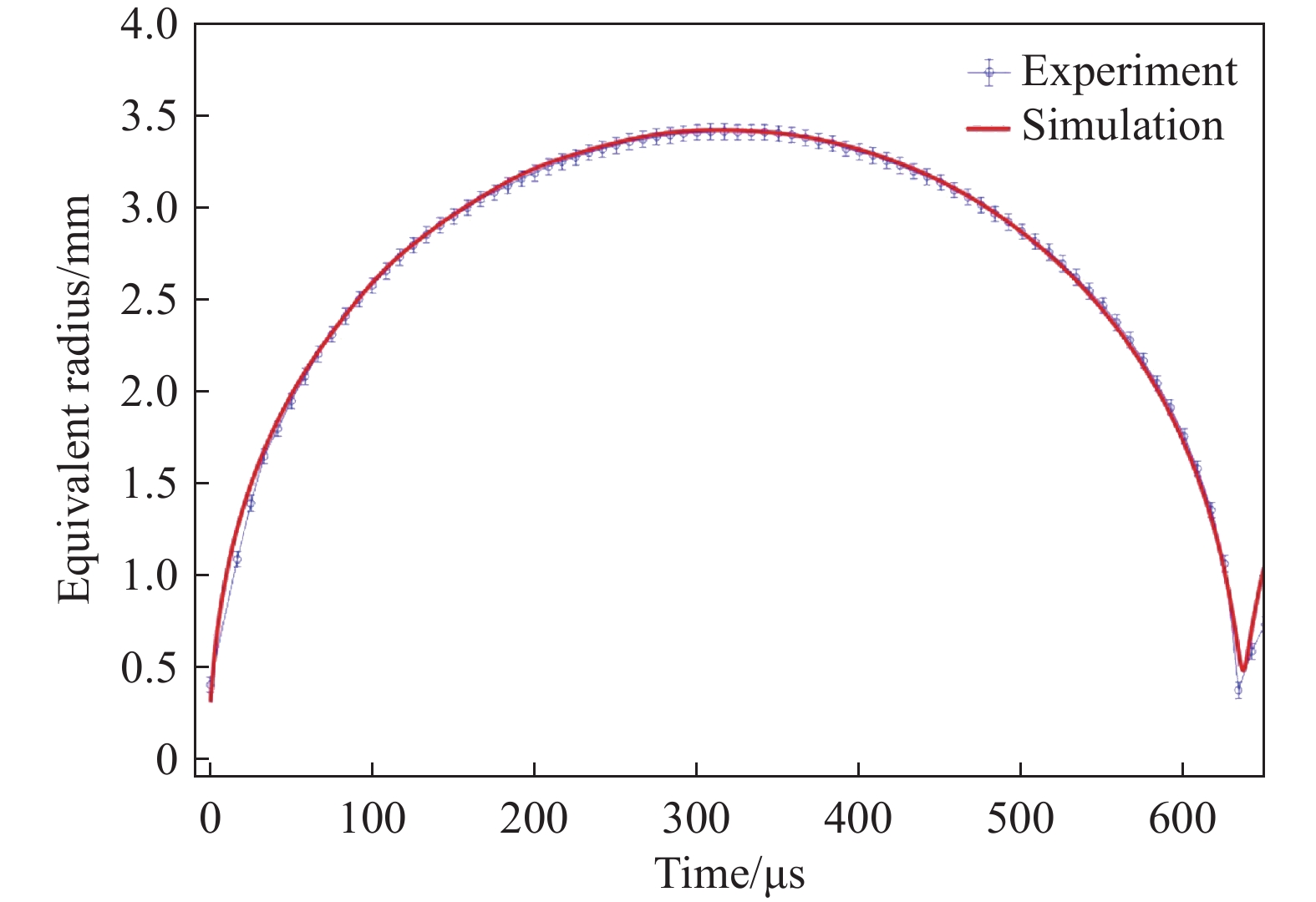
本文数值模拟结果与文献[11]的实验结果进行了对比验证。实验中，脉冲激光束通过离轴反射镜汇聚到水中，基于光学击穿原理，产生一个振荡的空化泡，通过改变自由面的位置调节无量纲距离$\gamma$的大小。在数值模拟中，通过对比无限水域工况下实验结果与数值模拟结果，获得了数值模拟中空泡的初始压力和半径分别为30 MPa和0.3 mm，如图3所示。

图  3  空泡在无限水域振荡半径的数值与实验结果对比

Figure  3.  Comparison of bubble equivalent radius between experiment and numerical simulation in an unbounded liquid

下载: 全尺寸图片 幻灯片

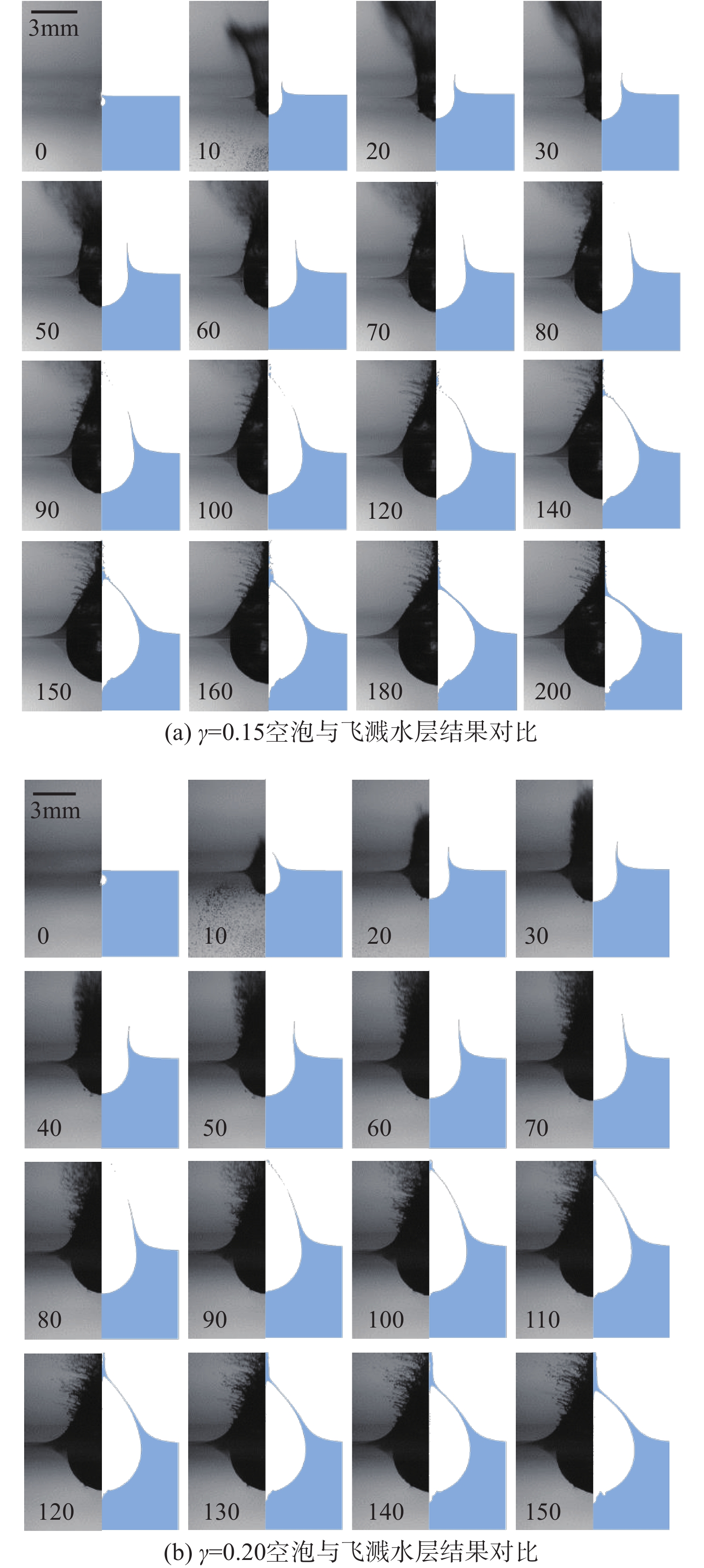
以初始压力30 MPa、半径0.3 mm为初始条件，数值模拟了空泡在靠近自由面时发生的通气、水层飞溅等过程。图4分别是$\gamma$ = 0.15、0.20时实验观测和数值模拟的结果对比。图中0时刻为高速相机开始采样时刻。$\gamma$ = 0.15工况下，空泡在t = 10 μs时刻发生通气，飞溅水层初始呈“V”型向外扩张，随后飞溅水层逐渐向中心收缩，并在t = 124 μs附近完成闭合。$\gamma$ = 0.20工况下，在空泡膨胀作用下，自由面在t = 10 μs向上飞溅并在t = 97 μs附近闭合。整体而言，针对空泡与飞溅水层的形态结果，数值模拟与实验结果吻合较好，证明当前数值方法可用来探究空泡通气、自由面液面飞溅及闭合强耦合作用。

图  4  实验与数值模拟结果对比（左侧为实验结果，右侧为仿真结果，深蓝色为液体，白色为气体，时间单位为μs ）

Figure  4.  Comparisons between experimental (left) and numerical simulation (right) results, $\gamma$ = 0.15, 0.20 (The deep blue and white present the phases of liquid and gas, respectively. The time unit is μs)

下载: 全尺寸图片 幻灯片

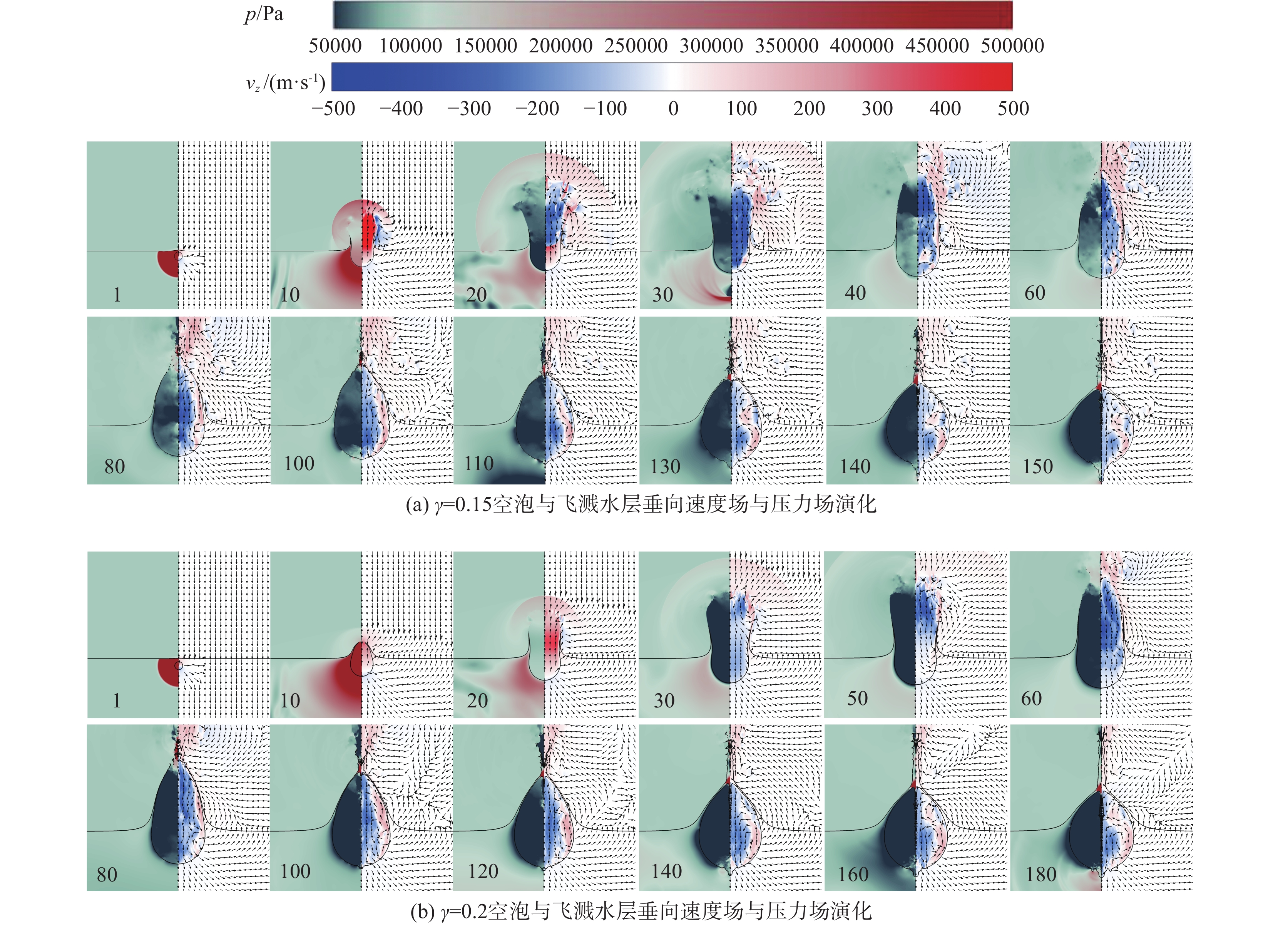
图5展示的是$\gamma$ = 0.15和$\gamma$ = 0.20时空泡发生通气、自由液面飞溅以及再闭合过程的压力场与垂向速度场的演化过程。$\gamma$ = 0.15时，空泡在t = 10 μs发生通气，空泡内气体沿通道快速向外喷出，气体喷出速度可达到1300 m/s，并在流场中产生了明显的冲击波。在气体喷出约20 μs，空泡内压力降低至20 kPa，随着空泡继续膨胀，外界空气通过水层围成的通道快速向内侵入，最高速度可达670 m/s（t = 40 μs左右），同时，通道受到内外压强差作用快速增大。另一方面，在飞溅水层外侧产生了明显的旋涡，并逐渐向上方移动，与图4（a）中实验中观察到的现象吻合。$\gamma$ = 0.20时的空泡和飞溅水层演化规律与$\gamma$ = 0.15基本相似，在t = 30 μs外界气体开始侵入空泡内部，最大速度可达到420 m/s，通道内外压强差达到70 kPa左右。

图  5  自由液面飞溅及闭合过程（左侧为压力场，右侧为垂向速度场结果，时间单位为μs）

Figure  5.  Pressure fields (left) and vertical velocity fields (right) during free surface splash and closure processes when γ = 0.15, 0.20 (The time unit is μs)

下载: 全尺寸图片 幻灯片

2.2   闭合飞溅水层受力分析

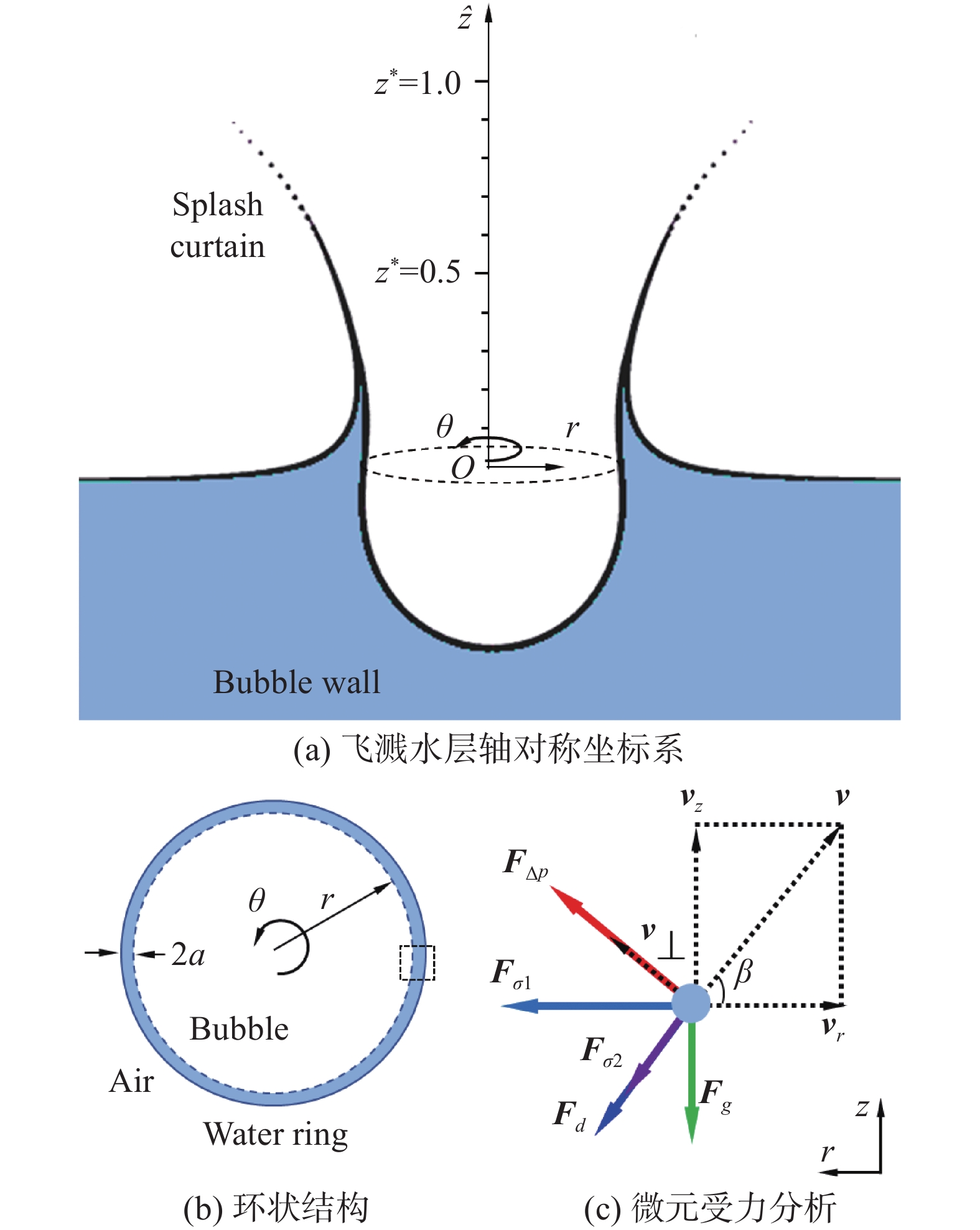
由图5可知，空泡内气体首先向外部排出，由于空泡膨胀，空泡内部压力低于外界压力，外界气体逐渐进入空泡内部。为了分析水层闭合机制，参考Eshraghi等^[20]采用贴体坐标系对于小球入水诱导的飞溅水层进行的受力分析，本文采用固定坐标系对水层横截面进行受力分析。如图6（a）所示，对飞溅水层建立轴对称坐标系，将坐标原点设在自由面上，垂直向上为$\widehat{z}$轴正半轴，由原点向空泡向外膨胀方向为$r$正向。${z}^{*}=\widehat{z} /{h}_{c}$表示无量纲化后的垂向高度，${h}_{c}$为飞溅水层闭合位置到自由面的高度，所以${z}^{*}$的范围是0～1。

图  6  飞溅水层模型示意图

Figure  6.  Schematic of the splash induced from the free surface

下载: 全尺寸图片 幻灯片

假设飞溅水层是轴对称分布，不考虑其在$\theta$方向的分布，故在无量纲垂向高度${z}^{*}$，可将飞溅水层视为厚度为2$a$、质量为$\displaystyle{\int }_{0}^{2{\text{π}} }{\rho }_{l}{\text{π}} {a}^{2}r{\rm{d}}\theta$、关于$\widehat{z}$轴呈轴对称的环状结构，如图6（b）所示。取环状结构上的微元进行受力分析，如图6（c）所示，此微元主要受到空气阻力（${\boldsymbol{F}}_{\mathit{d}}）$、表面张力$（{\boldsymbol{F}}_{\mathit{\sigma }1}$、${\boldsymbol{F}}_{\mathit{\sigma }2}$）、水层两侧的压差力$（{\boldsymbol{F}}_{\Delta \mathit{p}}$）以及重力（F_g）的作用。

环状水层受到空气阻力为：

其中：${C}_{D}$为阻力系数，${\rho }_{{\rm{g}}}$为空气密度，$a$为水环厚度的一半，$\boldsymbol r\left(t\right)$为水环距离$\widehat{z}$轴的距离，v为速度，阻力方向与速度$\boldsymbol v$方向相反。水环受到两个方向的表面张力^[29-30]，作用于水环周向的表面张力，方向为径向并指向空泡内，可表示为：

式中$\mathrm{\sigma }=0.072$ N/m为表面张力系数。水层对该水环的拉力，方向与速度方向垂直，可表示为：

重力方向为$\widehat{z}$轴负向，可表示为：

水环两侧压差带来的压差力，方向与速度$\boldsymbol{v}$方向垂直，促使水层扩张或闭合，压差力可表示为：

其中$\Delta p\left(t\right)$为水环两侧内外压差。为分析飞溅水层在闭合过程中受到的主要驱动力，以$\gamma$ = 0.20工况为例，根据本文数值模拟获取的速度场与压力场结果计算上述各力。其中，飞溅水层闭合的控制条件为：

式中${\boldsymbol{v}}_{\mathit{r}}\left(t\right)$为水环径向速度。

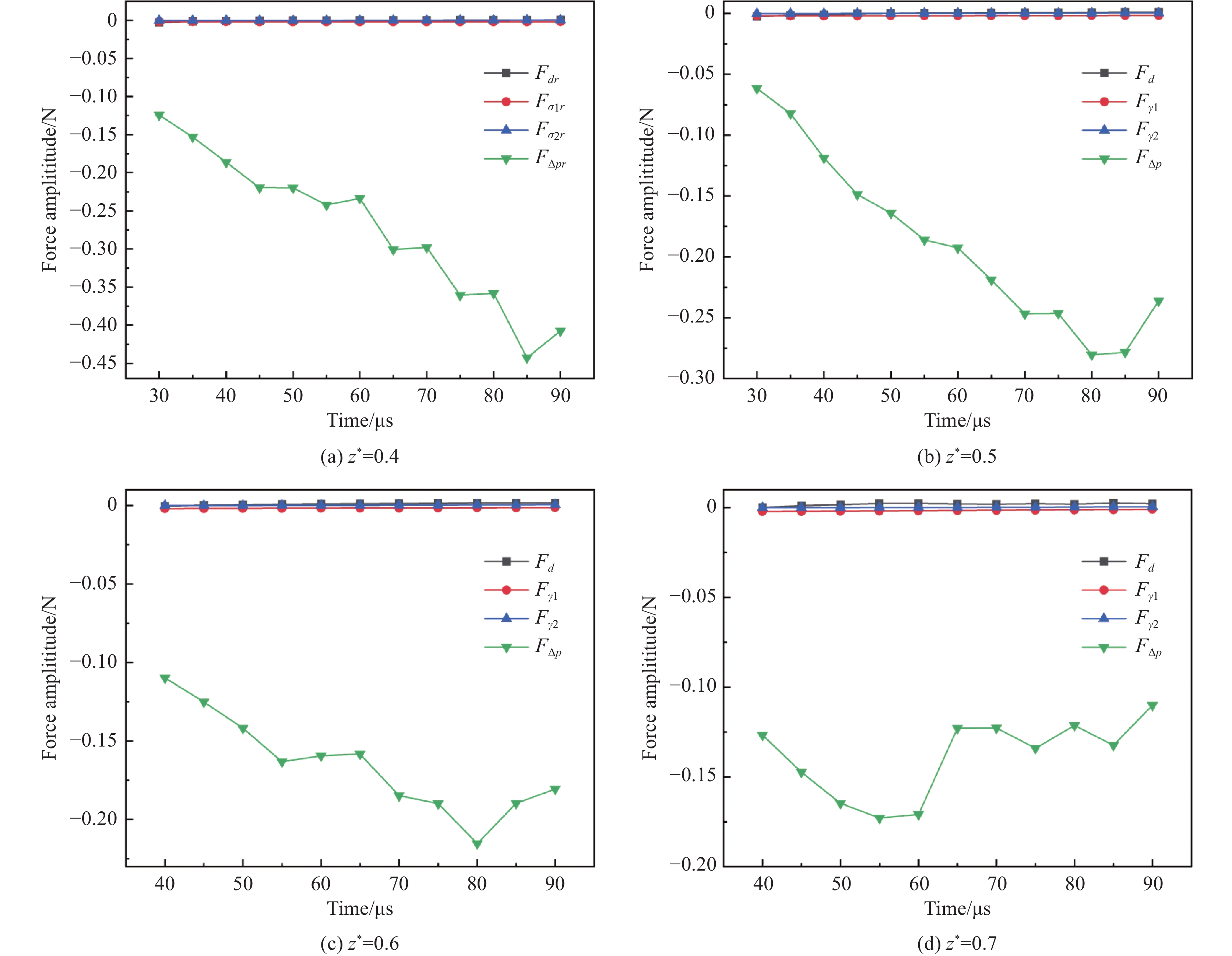
考虑到飞溅水层闭合是由于各力在$r$方向的共同作用，故对各力在径向方向的分量进行分析，如图7所示。${\boldsymbol{F}}_{\mathit{d}\mathit{r}}$、${\boldsymbol{F}}_{\mathit{\sigma }1\mathit{r}}$、${\boldsymbol{F}}_{\mathit{\sigma }2\mathit{r}}$、${\boldsymbol{F}}_{\Delta \mathit{p}\mathit{r}}$分别表示水环受到的空气阻力、表面张力以及压差力在径向方向的分量，正负号代表各力的方向，其中沿径向向外为正方向。由图5可知，在t = 40 μs左右，外界气体沿通道均匀向内流动，外界气压大于通道内部压力，飞溅水层开始向中心收缩，从此开始统计各力在径向方向分量。

图  7  $\gamma$ = 0.20时不同无量纲垂向高度${z}^{*}$水环所受各力在径向方向的分量

Figure  7.  The radial components of forces acting on the water ring at different dimensionless vertical heights normalized by ${h}_{c}$ at $\gamma$ = 0.20

下载: 全尺寸图片 幻灯片

由图7可知，飞溅水层闭合的过程中，阻力、表面张力在径向方向的分量基本保持不变，稳定在0 N（${o}({10}^{-3})$）附近，压差力在水平方向的分量远大于阻力与表面张力。当无量纲垂向高度${z}^{*}$在0.4～0.6附近，水环受到的压差力随着时间演化呈现逐渐增加的趋势。结合图5通道内速度场与压力场可知，外界空气不断侵入通道内，且气流逐渐稳定，使得通道内压力逐渐增加。根据公式（10）可知，$\boldsymbol r\left(t\right)$对于压差力的影响更大，空泡的继续膨胀导致了图7（a、b、c）中水环内外压差力逐渐增加。当${z}^{*}$在0.7左右，水环受到的压差力出现较大的波动，结合速度场可知，${z}^{*}=0.7$处通道内气体流动不均匀，导致了水环两侧压差力的波动。总之，不同无量纲垂向高度${z}^{*}$上的水环受力分布规律基本相似，在飞溅水层闭合过程中，压差力始终占据主导地位，表面张力与空气阻力是可以忽略的。

2.3   飞溅水层闭合行为

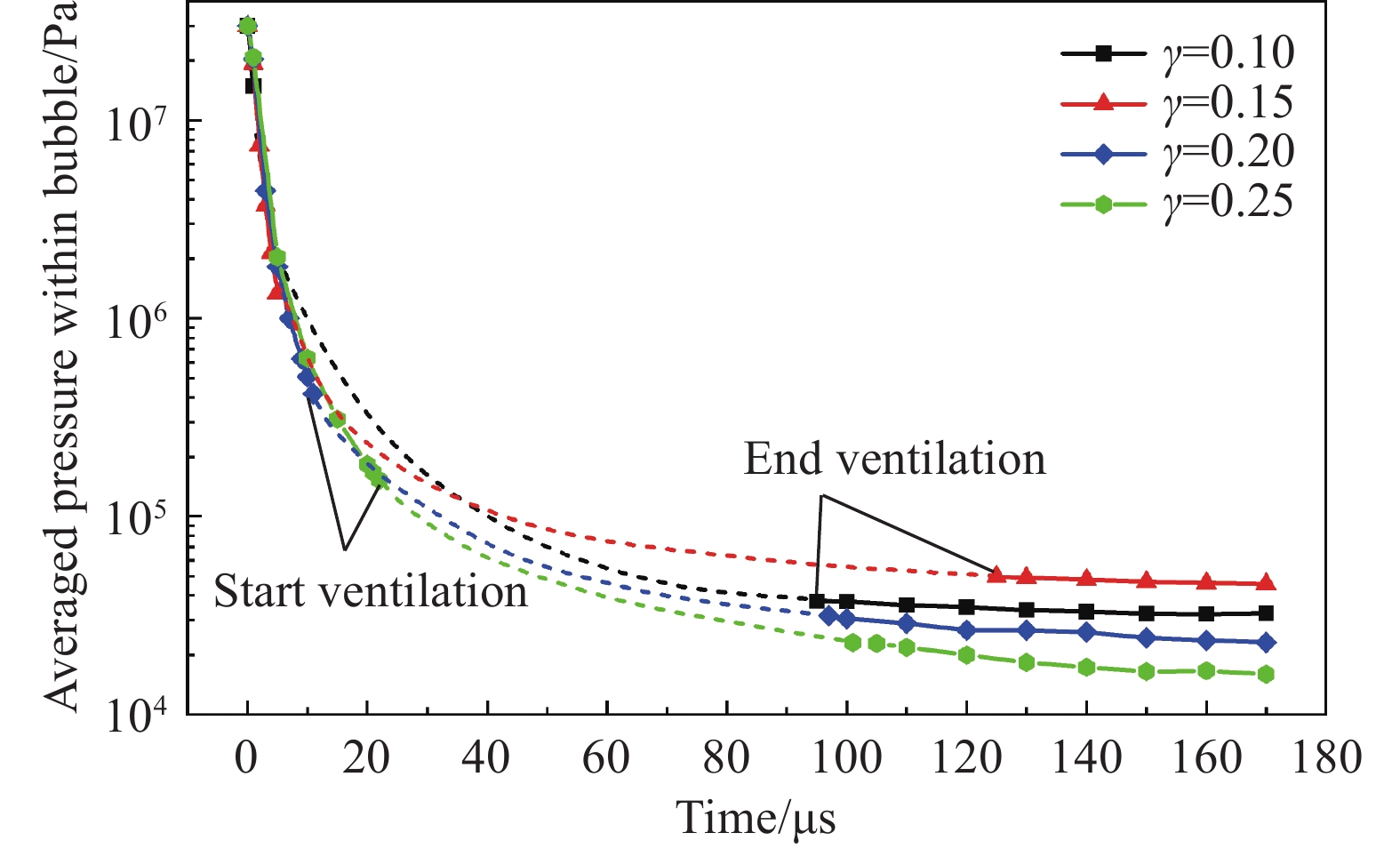
考虑到飞溅水层在闭合过程中主要受到内外压差的影响，故本文探究了不同$\gamma$和环境压力下的飞溅水层闭合特性。图8所示是不同$\gamma$空泡内平均压强随时间的演化关系，其中虚线表示空泡通气过程。空泡内气体的平均压强是通过将空泡内单元网格的体积与压强乘积积分后与空泡总体积的比值获取的。这里定义空泡在初始与外界空气发生连通的时刻作为空泡通气开始的时刻${t}_{{\rm{start}}}$，飞溅水层闭合的时刻作为通气结束的时刻${t}_{{\rm{end}}}$，两者之差作为空泡发生通气的时间长度$\Delta t={t}_{{\rm{end}}}-{t}_{{\rm{start}}}$，飞溅水层闭合的位置与初始时刻自由面之间的高度差作为飞溅水层的闭合高度${h}_{c}$, 如图9（b）所示。

由图8中可知，空泡在初始发生通气时，空泡内部平均压力大于外界环境压力。结合图5速度场可知，针对$\gamma$ = 0.15的工况，空泡气体通过通道向外快速喷出，持续时间约20 μs，由于通道内外压差，外界空气逐渐向空泡内侵入，直至水层闭合。

图  8  不同$\gamma$情况下的空泡内部平均压强随时间的演化

Figure  8.  Evolution of averaged pressure in the bubble with time for different $\gamma$

下载: 全尺寸图片 幻灯片

图  9  不同$\gamma$时空泡通气时间、飞溅水层闭合高度、水层闭合形态对比

Figure  9.  Bubble ventilation time, splash closure height, and the morphology of splash closure for different $\gamma$

下载: 全尺寸图片 幻灯片

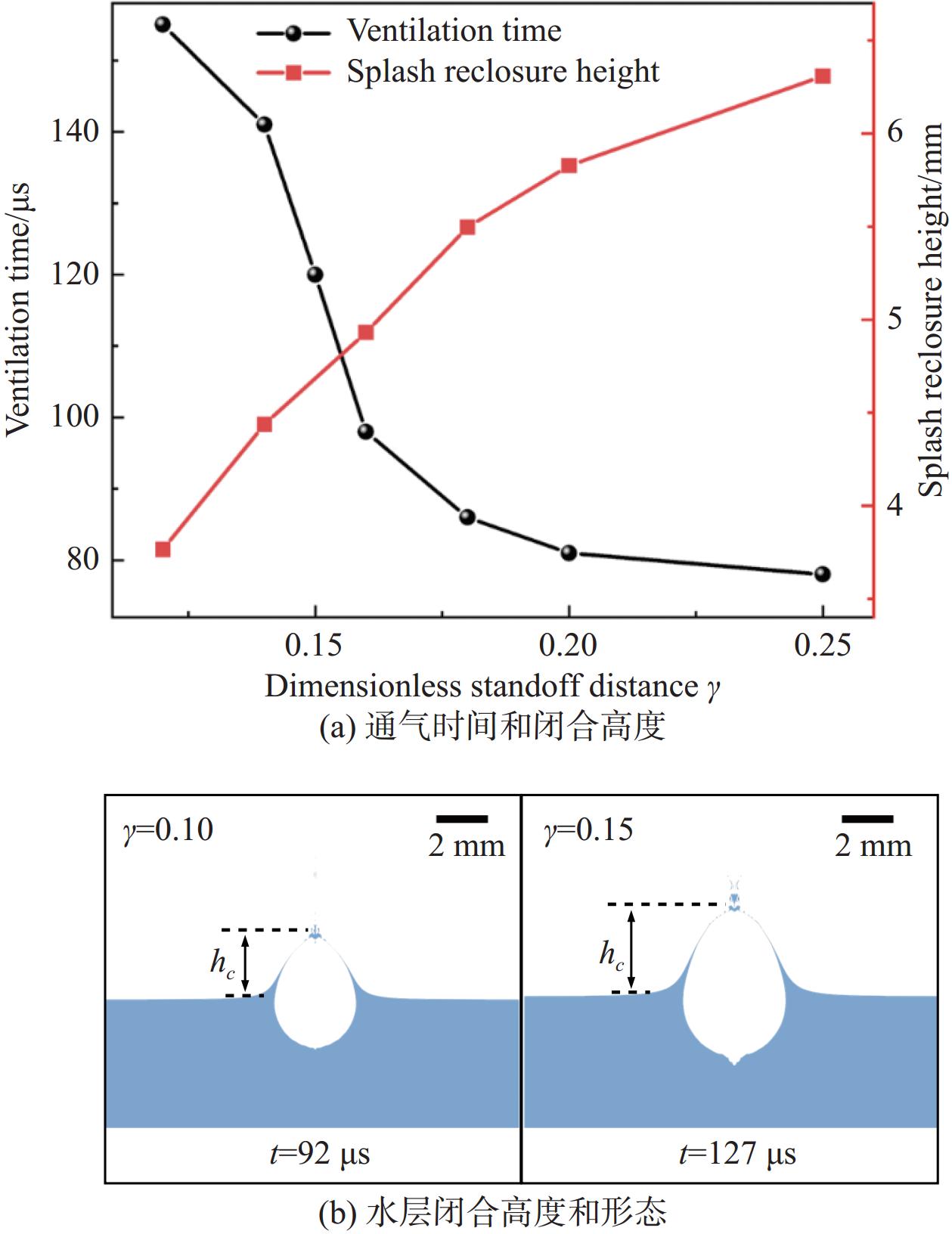
图9展示的是不同$\gamma$情况下空泡通气时间、飞溅水层闭合高度以及水层闭合时刻的形态。

随着$\gamma$的增加，空泡发生通气的时间逐渐减少，空泡在$\gamma$ = 0.15附近通气时间急速下降，在$\gamma$ = 0.20之后基本保持稳定，维持在80 μs左右。当$\gamma$逐渐增大时，空泡开始发生通气的时间逐渐延后，空泡的势能更多地传递给上方水层，使得水层动能增加，获得较大的垂向速度，使得水层闭合的高度随$\gamma$的增加呈现不断增加的趋势。

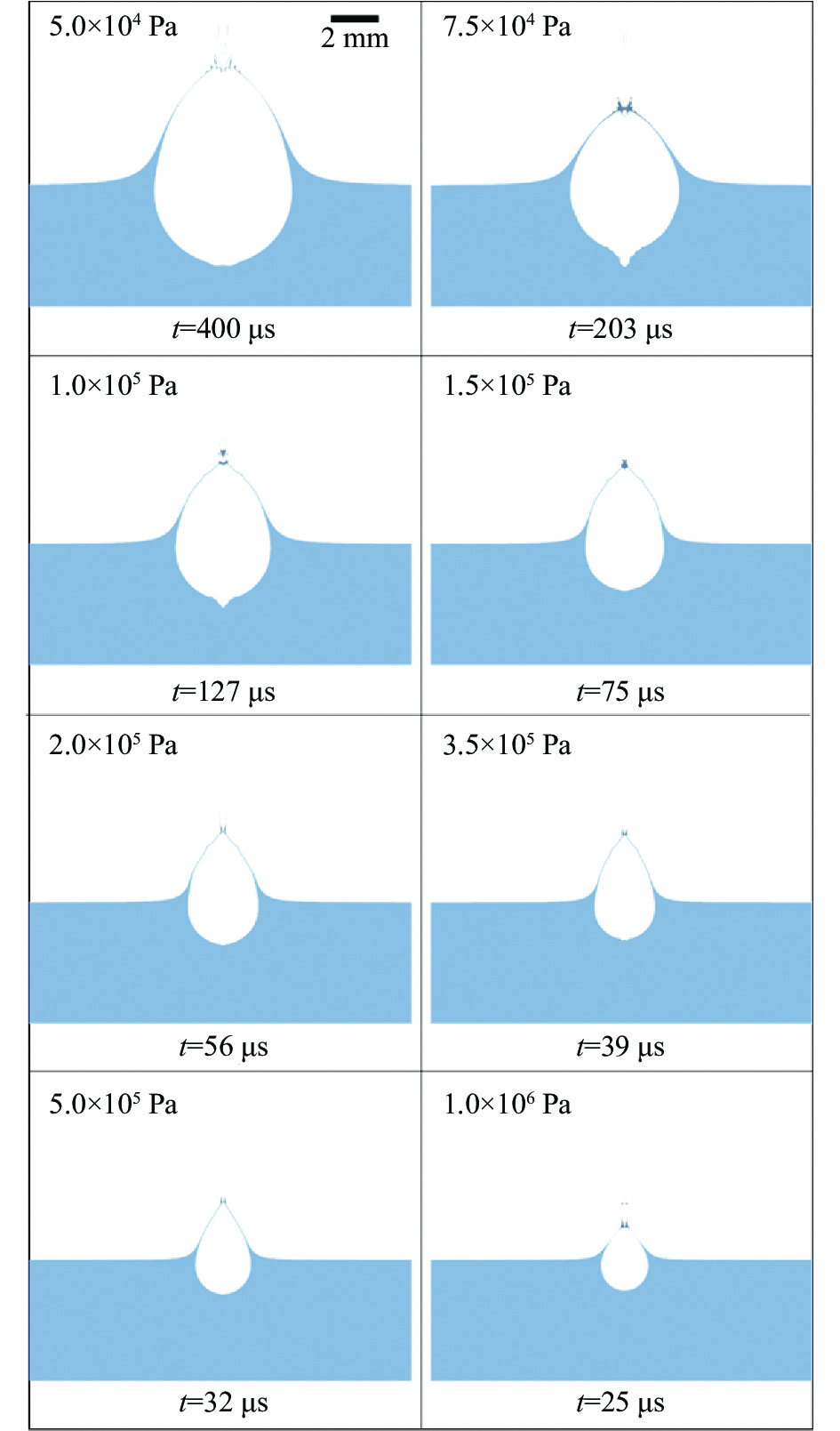
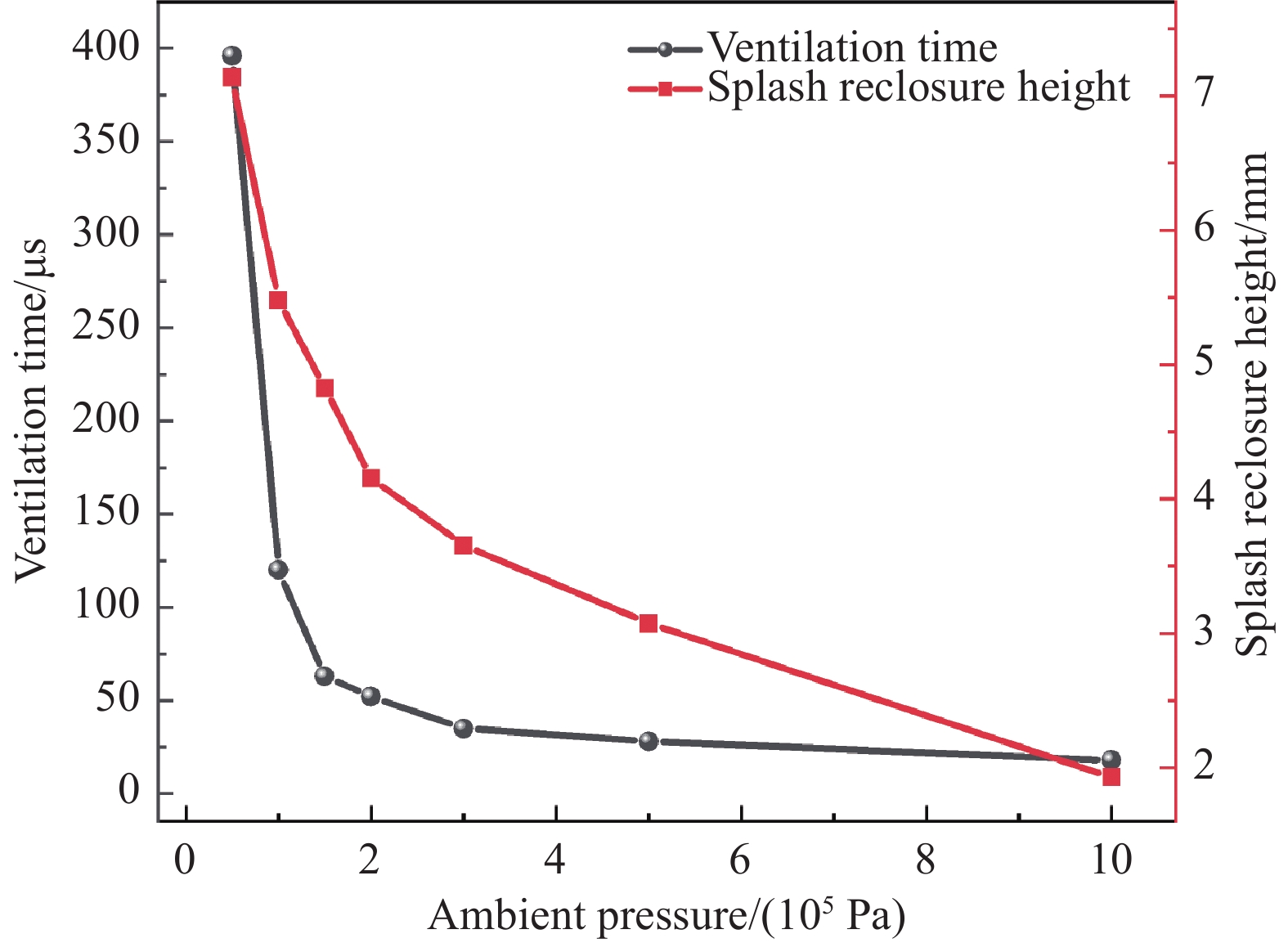
同时，在$\gamma$ = 0.15下，对比分析不同环境压力对飞溅水层闭合行为的影响，如图10所示。随着环境压力的增加，空泡形态基本相似，飞溅水层闭合高度、闭合的时刻逐渐减小。图11定量给出了$\gamma$ = 0.15时，空泡通气时间、飞溅水层闭合高度随不同环境压力的演化。空泡通气时间和飞溅水层闭合高度随着环境压力的增加逐渐减少。当环境压力小于1×10⁵ Pa时，通气时间迅速增加；当环境压力大于1×10⁵ Pa时，通气时间逐渐减少并基本稳定在20 μs左右。这是因为当环境压力增加，空泡初始时刻内外压差减少，导致了空泡振荡强度减弱，削弱了空泡诱导自由面飞溅水层的发展和空泡通气过程，使得空泡较晚发生通气，飞溅水层较早发生闭合，缩短了空泡通气时间。

图  10  $\gamma$ = 0.15时不同环境压力下的飞溅水层闭合形态

Figure  10.  Morphology of splash closure for different ambient pressure conditions at $\gamma$ = 0.15

下载: 全尺寸图片 幻灯片

图  11  $\gamma$ = 0.15时空泡通气时间和飞溅水层闭合高度随环境压力的演变

Figure  11.  The evolutions of bubble ventilation time and splash closure height under different ambient pressure at $\gamma$ = 0.15

下载: 全尺寸图片 幻灯片

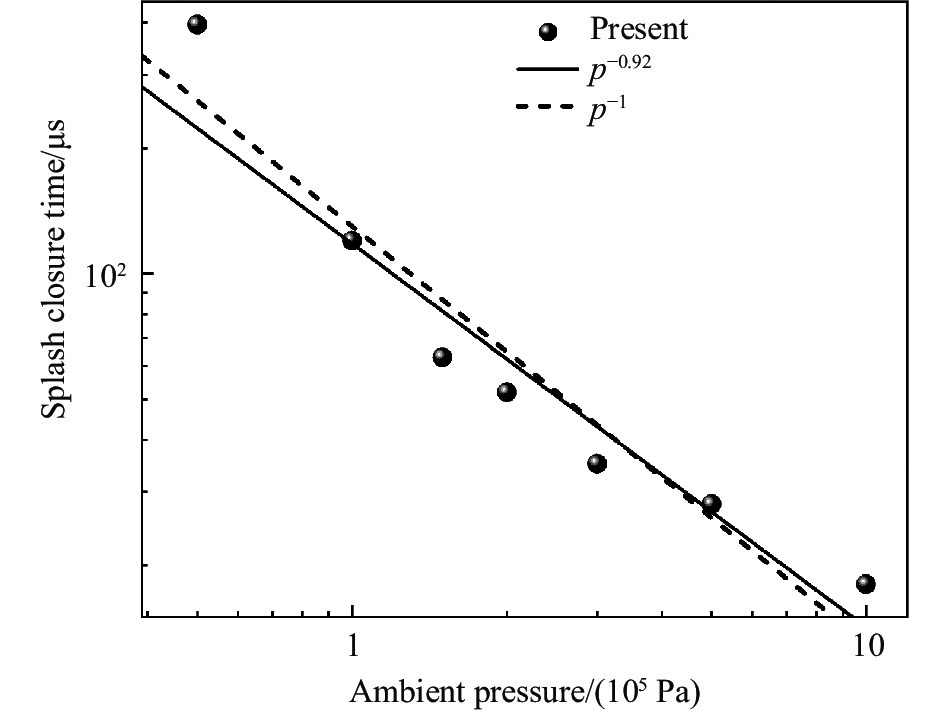
图12展示了$\gamma$ = 0.15工况下飞溅水层闭合时间随环境压力的演变。图中实心圆点来自本文数值模拟，虚线为Lee等^[31] 研究中获得的幂次律关系。Lee发现在小球入水后，水层闭合时间与环境压力之间近似满足$t\sim {p}^{-1}$关系。本文发现，在环境压力为$5{\times 10}^{4}$～${1\times10}^{6}$ Pa时，水层闭合时间与环境压力之间近似满足$t\sim {p}^{-0.92}$关系。这是因为通气空泡诱导与入水问题形成的飞溅水层闭合过程的受力类型和主要驱动力相同，均主要由水层两侧的压差力主导。因此，二者幂次律关系相似，差异可能来源于实验观测和数值模拟中水层闭合时间的测量误差。

图  12  $\gamma$ = 0.15时飞溅水层闭合时间随环境压力的演变

Figure  12.  The evolutions of splash closure time under different ambient pressure at $\gamma$ = 0.15

下载: 全尺寸图片 幻灯片

3.   结　论

本文对空泡与自由面强耦合作用诱导的飞溅水层闭合行为进行了数值模拟研究。基于开源的OpenFOAM平台，采用有限体积法直接求解N-S方程，并使用VOF方法捕捉气液界面。得到如下结论：

1）飞溅水层在闭合过程中的主要驱动力是水层两侧压差力，重力、表面张力与空气阻力可以忽略。

2）空泡通气时间随着无量纲距离$\gamma$和环境压力的增加而减少，飞溅水层闭合时的高度随着无量纲距离$\gamma$的增加而增加，随着环境压力的增加而不断减小，水层闭合时间与环境压力之间近似满足$t\sim {p}^{-0.92}$关系，该幂次律与入水问题的$t\sim {p}^{-1}$相似。

本文数值模拟了空泡通气、水层飞溅与闭合等现象，旨在为二者的强耦合作用研究提供参考。在未来的研究中，需要引入粒子图像测速等技术，定量测量通气过程的速度场演化，为数值模拟研究提供重要数据对比。同时，在理论建模方面，考虑水层演化对空泡行为的影响，建立二者双向强耦合物理模型。