Optimization design method of automobile aerodynamic shape based on multi-fidelity deep neural network
-
摘要:
在汽车气动外形优化设计中，往往需要大量的高精度CFD数据作为支撑。然而，高精度CFD数据获取难度大、成本高。为了缓解汽车气动优化设计中气动特性评估精度和效率之间的矛盾，根据迁移学习与数据融合的思想，提出了一种基于多精度深度神经网络（multi-fidelity deep neural network, MFDNN）的汽车外形优化设计方法，以减少优化设计中所需的高精度数据个数，从而有效提升优化速度、降低优化成本。将所发展的优化方法应用于快背式MIRA标准模型减阻优化设计中，优化结果表明，该方法能够充分融合不同精度数据所蕴含的知识，加速气动外形优化进程，提升优化效率。以收敛用时作为评价指标，在取得相近或更优优化结果的前提下，基于多精度神经网络的优化框架的收敛速度是基于单精度神经网络的离线优化框架的5.85倍，是基于单精度神经网络的在线优化框架的2.81倍。
-
关键词:
- 多精度深度神经网络模型 /
- 汽车气动外形优化设计 /
- 迁移学习 /
- 数据融合
Abstract:The optimization process of automobile aerodynamic design that requires a vast amount of CFD data, which are both expensive and time-consuming to acquire, is arduous and costly. To get out of this predicament—the conflict between accuracy and efficiency—we devise an innovative automobile shape optimization technique relying on the Multi-fidelity deep neural network (MFDNN) aerodynamic model based on transfer learning and data fusion. Applying the developed optimization method to the drag reduction optimization design of the fast-back MIRA standard model demonstrates that the method can fully integrate the knowledge contained in different fidelity data, accelerate the aerodynamic shape optimization process, and improve the optimization efficiency. Specifically, the convergence speed of the optimization framework based on multi-precision neural network is 5.85 times that of the offline optimization framework based on single-precision neural network and 2.81 times that of the online optimization framework based on single-precision neural network.
-
0. 引 言
降低气动阻力是减少汽车能耗、增加续航里程的一项有效措施，能有效提升汽车的经济性与动力性能。近年来，随着计算机性能的不断提升，结合计算流体力学（Computational Fluid Dynamics, CFD）与优化算法的气动外形优化设计技术逐渐成为降低空气阻力、改善汽车气动特性的可靠手段。但汽车在高速行驶时，其表面附近的空气流动往往呈现出大规模分离和高度湍流化的特征，这给汽车的气动外形优化设计带来了困难，同时也增加了计算成本。为提高优化效率，基于代理模型的优化方法逐渐发展起来，其有效性也已被证实。代理模型是一种简化的数学模型，能够在较低的计算成本下快速预测汽车的气动特性[1]，其精度对优化效果有着决定性的作用。
当前，基于代理模型的优化设计方法在汽车气动外形优化设计领域应用十分广泛[2-4]。然而，目前的汽车优化设计普遍采用单精度优化设计方法，在优化过程中为了建立高精度的气动力模型，需要大量的高精度CFD数据用于气动力建模，这会增加汽车气动外形优化的成本与所需的时间。如何降低高精度代理模型的获取成本已成为汽车气动优化设计中的新挑战。
近年来，随着机器学习技术的不断发展，多精度数据融合建模成为气动力建模的研究重点。一些学者提出了使用低精度数据来改善代理模型精度的方法[5-13]。这种方法为应对获取高精度代理模型的挑战提供了一种有效的解决方案。受此启发，本文采用多种精度气动评估手段相融合的气动力建模思路对快背式MIRA模型的气动外形进行优化。在优化过程中，基于多精度神经网络，仅使用少量高精度数据，构建了高精度气动力模型，成功缓解了汽车气动优化设计中气动特性评估精度和效率之间的矛盾。经对比，本文提出的多精度优化设计方法相较于单精度优化设计方法显著提升了优化效率。
1. 汽车气动外形优化设计框架
1.1 优化模型的建立
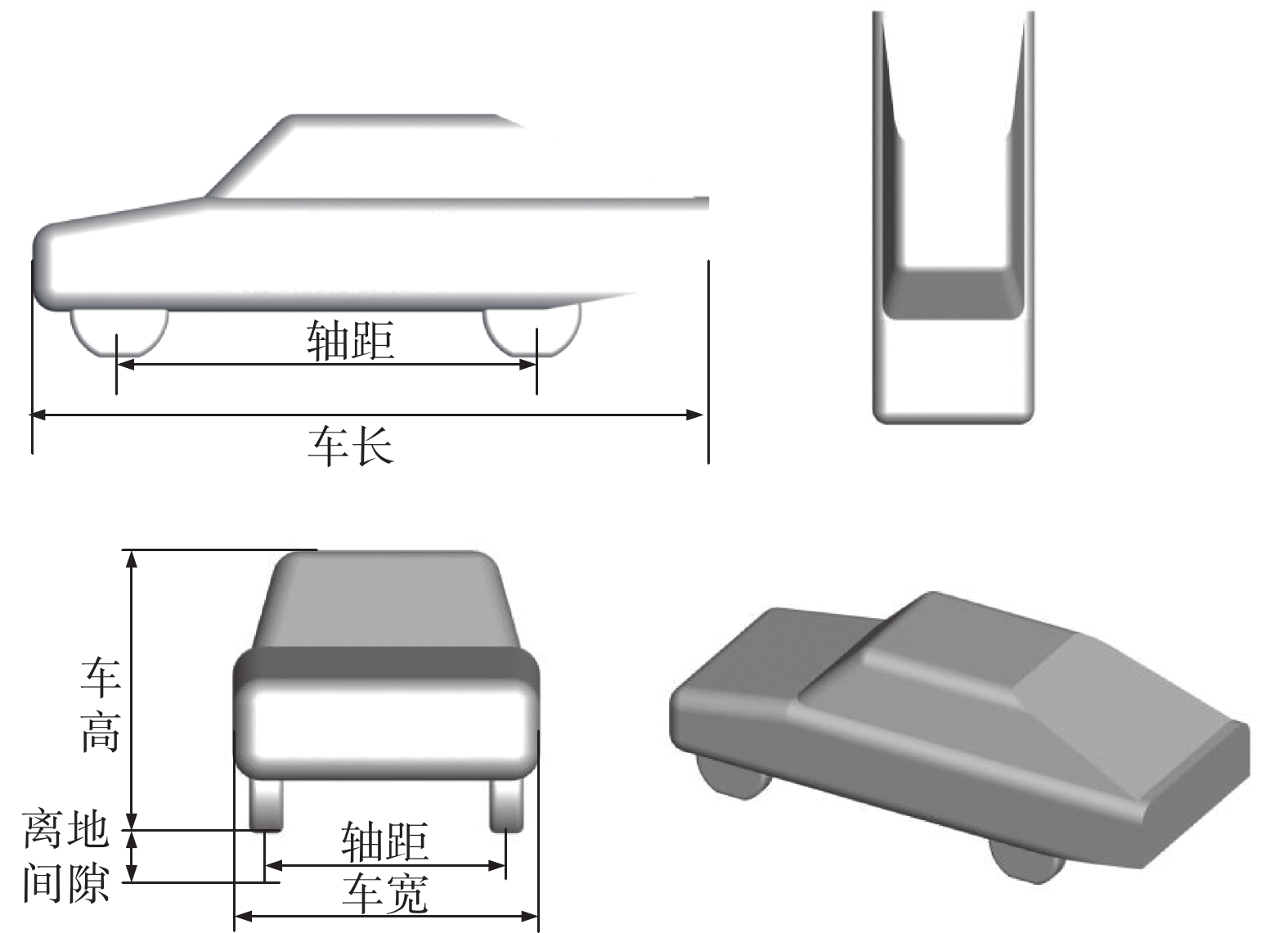
以快背式MIRA标准模型作为研究对象，进行单目标无约束减阻研究。快背式MIRA模型是英国汽车工业协会（Motor Industry Research Association）所提出的标准模型，其基本外形如图1所示，模型基本尺寸如表1所示。
表 1 模型基本尺寸表[14]Table 1. Quick-back MIRA geometry序号 名称 尺寸/mm 1 车长 4165 2 车宽 1625 3 车高 1421 4 轴距 2540 5 轮距 1270 6 离地间隙 205 7 轮胎半径 305 8 轮胎宽 180 在对MIRA模型进行气动外形优化设计时，必须根据工程实际设计要求，构建优化模型。本文构建的优化模型如下所示：
MinCD(Xi),Xi,min ⩽ (1) 其中， {{C}}_{{D}} 为快背式MIRA的阻力系数， {{X}}_{{i}} 为设计变量， {{X}}_{{i},\mathrm{m}\mathrm{i}\mathrm{n}} 与 {{X}}_{{i},\mathrm{m}\mathrm{a}\mathrm{x}} 分别是设计变量的下限与上限， {i} 为设计变量的维度。
1.2 整车CFD模型搭建
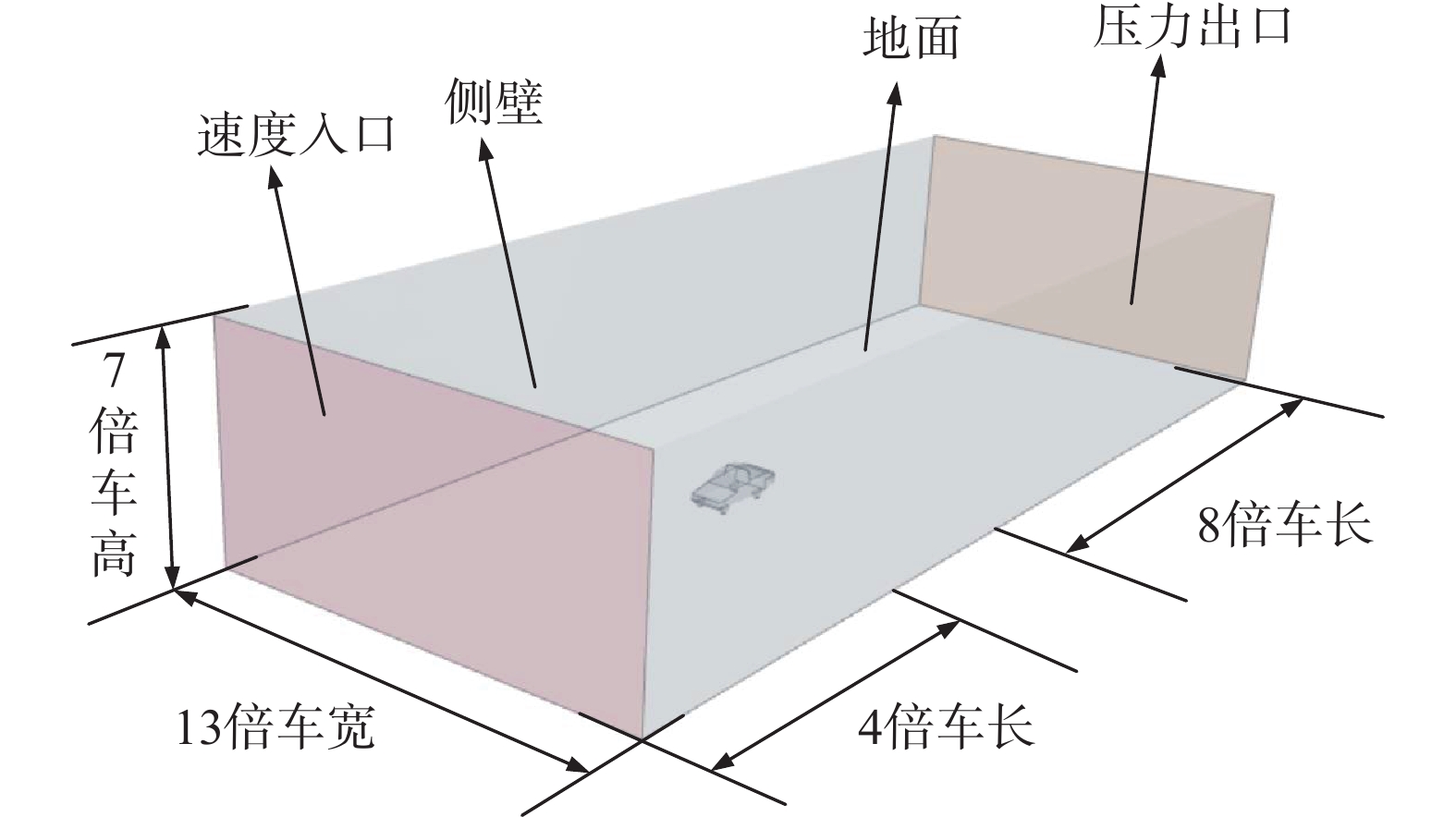
计算域如图2所示，汽车模型前端到入口的距离为4倍车长，到出口的距离为8倍车长。计算域的总高度为7倍车高，总宽度为13倍车宽，阻塞比为0.84%，小于5%，满足计算的要求。
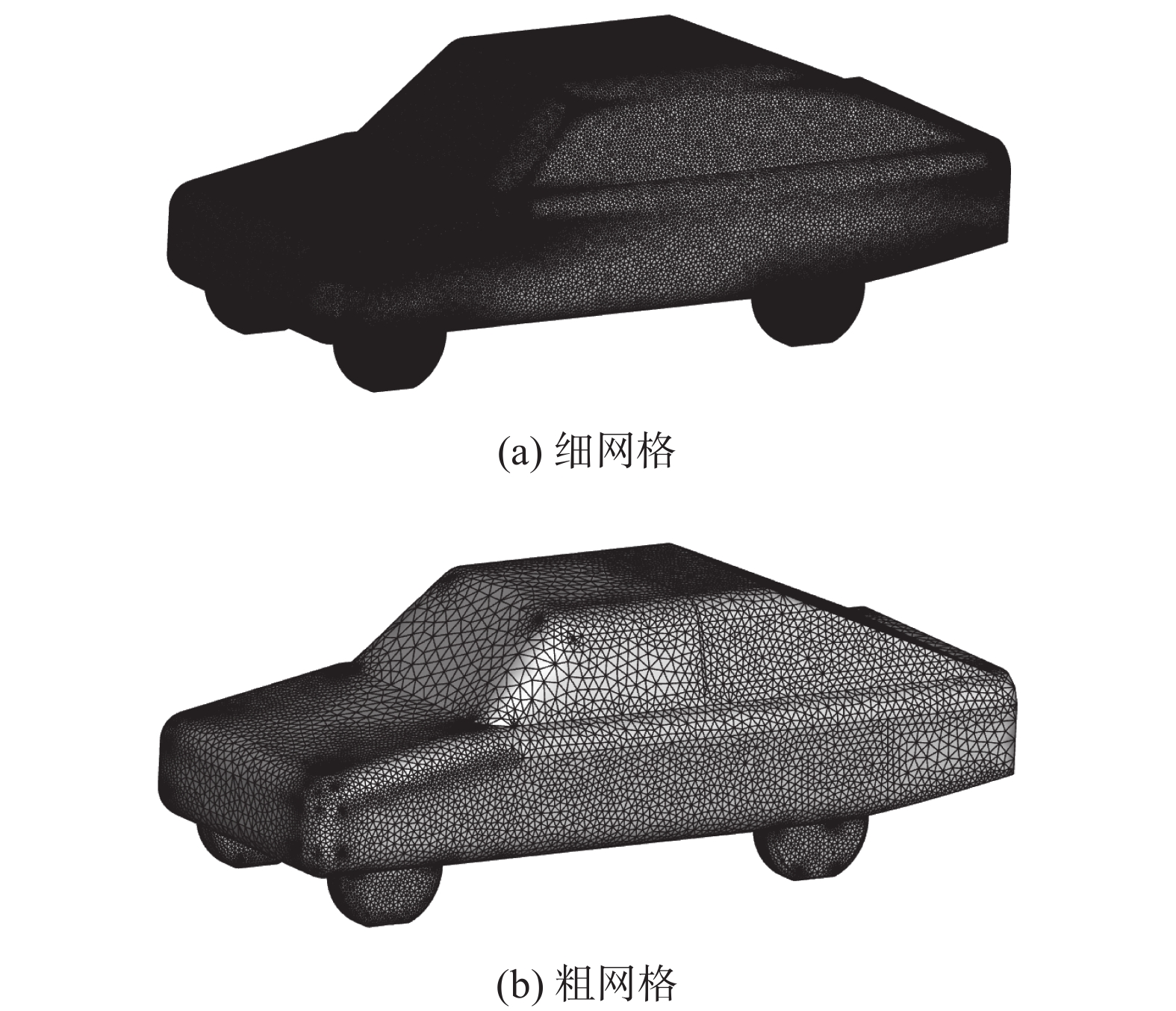
细粗网格的面网格分别如图3（a）和（b）所示。细网格的面网格尺寸为8～15 mm，共计生成面网格51万。其中，第一层附面层厚度为2 mm，增长率为1.2，附面层共5层。粗网格的面网格尺寸为20～50 mm，共有4万面网格，不设置附面层。
本文的数值仿真基于商业软件Star CCM+进行。设置气体类型为不可压气体，其密度 \mathrm{\rho } 为1.225 kg/m³。计算域入口边界类型为速度入口，速度大小为30 m/s。计算域出口为压力出口，压力值设置为相对值0 Pa。计算域壁面选用滑移壁面，汽车表面选用非滑移壁面。其中不同精度数据的求解格式及具体信息如表2所示。
表 2 求解格式设置Table 2. Computational settings高精度数据 低精度数据 网格量 4788261 795757 迎风格式 二阶 一阶 求解方程 N-S Euler 湍流模型 k{\text{-}}\varepsilon 模型 迭代次数 1300 550 数值模拟耗时 1.74 h 0.18 h 注：使用CPU为32 cores Inter Xeons Golden 6226R 2.9 GHz 对细网格做网格无关性验证，结果如表3所示。由结果可以看出，当网格量为480万时，阻力系数 {C}_{{D}} 趋于稳定，且与风洞数据相差较小，故本文采用体网格数目为480万的细网格进行模拟分析，其数值模拟耗时为1.74 h。然而，在使用单精度优化设计方法时，可能需要使用几十个甚至上百个高精度数据来构建高精度的气动力模型，这导致汽车气动外形优化设计非常耗时。如何降低高精度气动力模型对高精度数据的依赖性，成为设计人员面临的重大挑战。
表 3 不同网格量下数值仿真所得到的阻力系数Table 3. Resistance coefficients obtained by numerical simulations using different mesh sizes体网格数目 {C}_{D} 验证计算 284万 0.285 348万 0.279 480万 0.274 512万 0.274 风洞数据[15] 0.278 1.3 参数化设置及网格变形
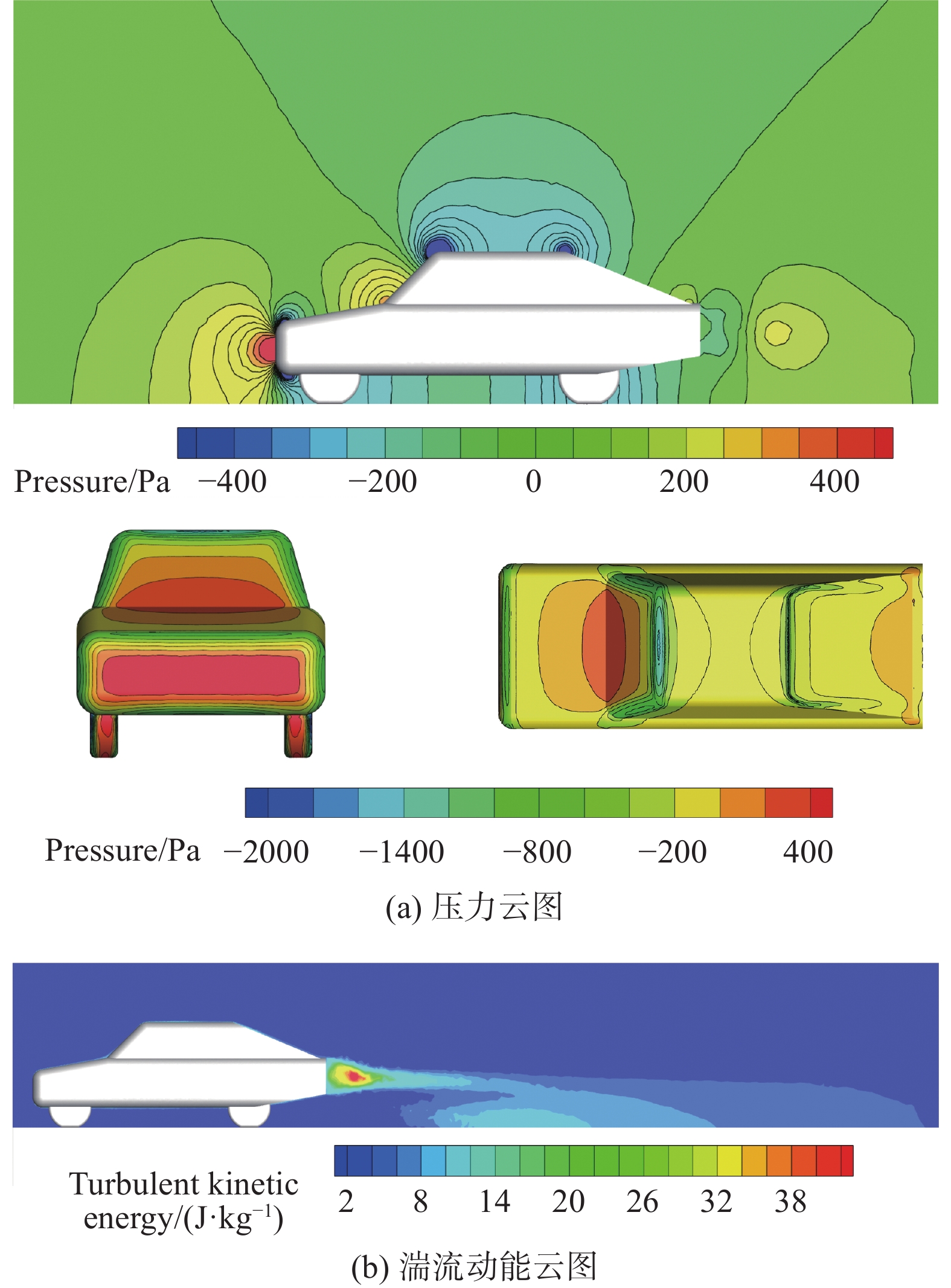
对基础MIRA模型进行数值模拟，获取汽车周围的流场特性，对流场进行可视化，压力云图与湍流动能云图分别如图4（a）与图4（b）所示。
![]()
图 4 基础模型压力云图与湍流动能云图Figure 4. Contours of the pressure and turbulent kinetic energy of the basic model基于对图4中压力云图、湍流动能云图的分析，找到流动分离较为剧烈的部位或湍流动能较强的区域。这些部位的气体分离与能量耗散较为严重，是引起气动阻力的重要因素，可对这些部位进行优化以减少气动阻力。
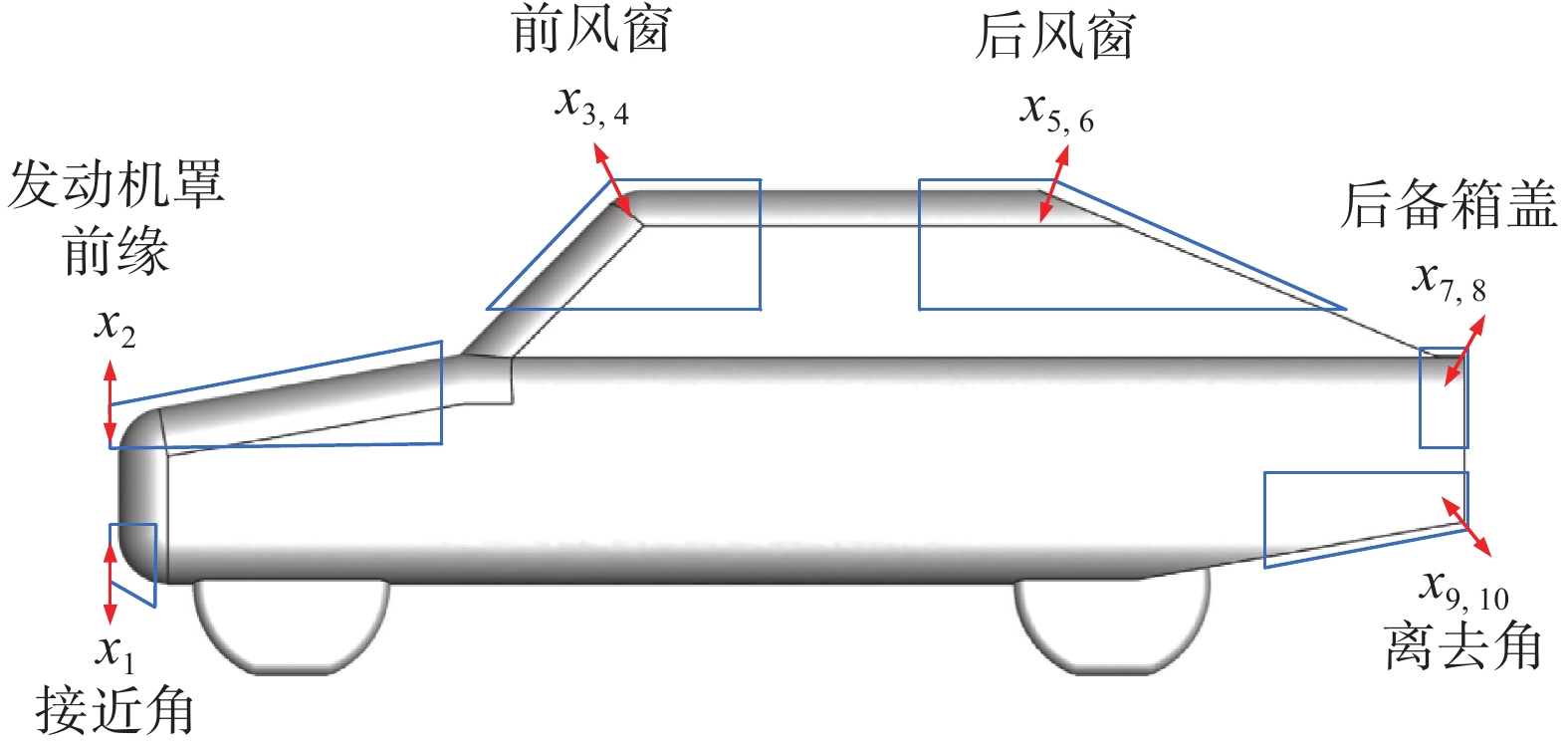
由图4中的云图可知，发动机罩前缘、底部前端、前风窗处压力梯度较大，汽车尾部存在较大的湍流区，故选取接近角、后备箱盖的z方向形变量以及发动机罩前缘、前风窗、后风窗、离去角的y方向形变量与z方向形变量作为设计变量，如图5所示。其中各个设计变量的变形上下限如表4所示，这里的变形上下限是绝对值。
表 4 所选取的设计变量的上下限Table 4. The upper and lower bounds of the selected design variables设计变量 {x}_{i} 变形范围/m 接近角z方向 [–0.015, 0.025] 发动机罩前缘z方向 [–0.04, 0.05] 前风窗y方向 [–0.01, 0.02] 前风窗z方向 [–0.01, 0.02] 后风窗y方向 [–0.03, 0.03] 后风窗z方向 [–0.04, 0.05] 后备箱盖y方向 [–0.04, 0.05] 后备箱盖z方向 [–0.04, 0.05] 离去角y方向 [–0.03, 0.03] 离去角z方向 [–0.05, 0.05] 1.4 优化器
优化器是汽车气动优化设计中的重要组成部分，主要用来寻找汽车外形最佳设计参数组合。本文选择教与学（teaching-learning-based optimization, TLBO）算法作为优化器进行迭代寻优，TLBO算法是一种全局类无参数化算法，具有良好的全局搜索能力。
2. 基于多精度深度神经网络的汽车气动优化设计
为了提升基于单精度代理模型的气动优化方法的效率，并降低高精度气动力模型对高精度数据的依赖性，本文提出了一种基于多精度深度神经网络（multi-fidelity deep neural network, MFDNN）的汽车气动外形优化框架。在这个优化框架中，利用低精度数据来提升气动力模型的精度，成功地减少了高精度气动力模型对高精度数据的依赖性。
本章采用了基于MFDNN的汽车气动外形优化框架，与基于深度神经网络（deep neural network, DNN）的汽车气动外形优化框架进行对比，对快背式MIRA模型进行减阻优化，以验证多精度神经网络在汽车气动优化设计中的优越性。
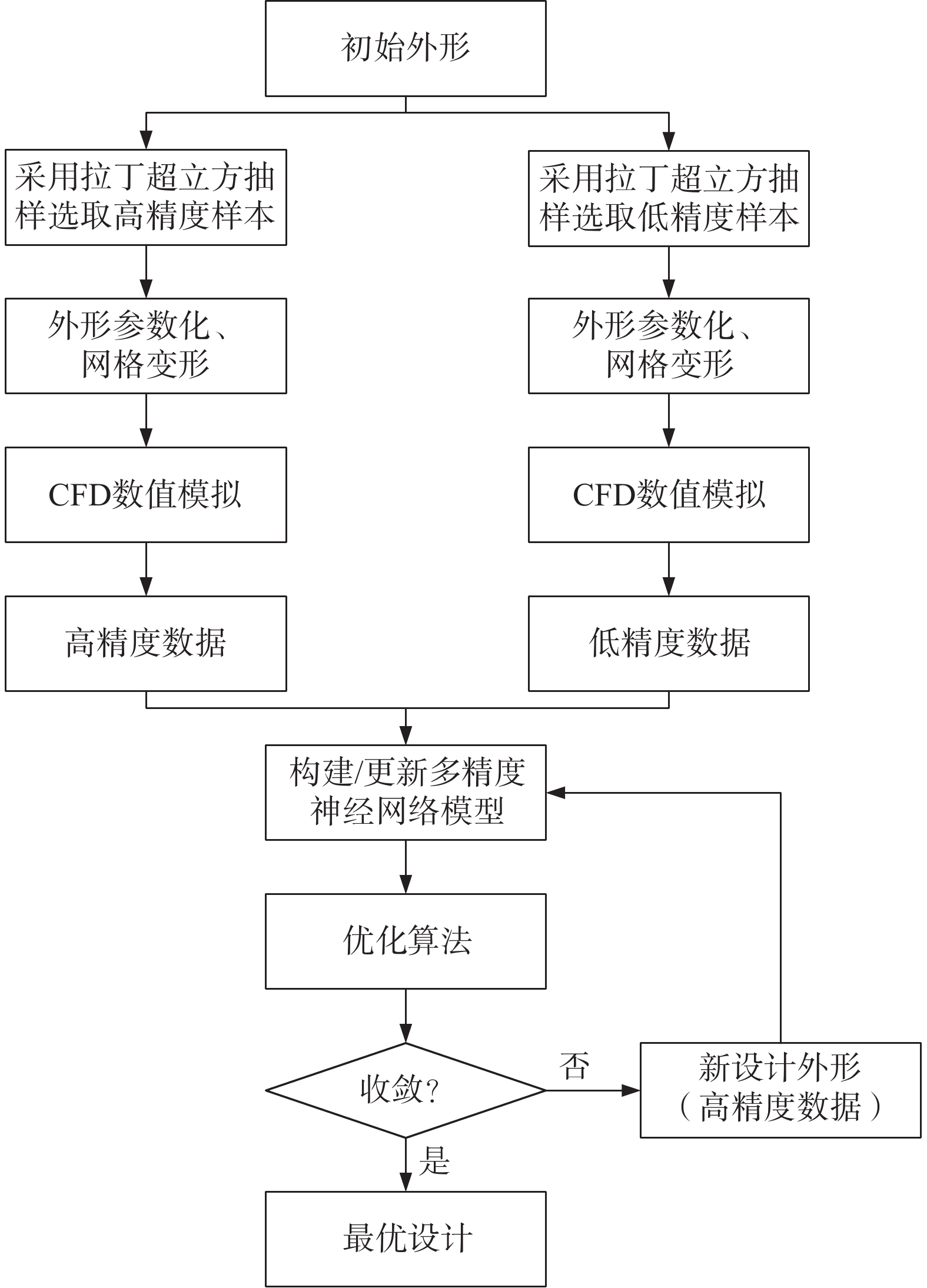
基于多精度神经网络模型的汽车气动外形优化框架示意图如图6所示。首先通过拉丁超立方抽样法，选取高精度样本点与低精度样本点，根据所选取的样本点进行网格变形与气动分析，获取所对应的阻力系数 {C}_{D} ，构建实验设计（design of experiments, DOE）矩阵；然后基于所建立的DOE矩阵，建立MFDNN模型，结合优化算法得到基于多精度神经网络模型的汽车气动外形优化框架下的最优设计。
![]()
图 6 基于多精度神经网络模型的优化框架Figure 6. Optimization framework based on multi-fidelity neural network model2.1 多精度深度神经网络
MFDNN构建过程中最重要的部分就是发现并利用低精度数据与高精度数据之间的相关性。根据广义自回归原理，Meng和Karniadakis [16]将高精度数据与低精度数据之间的相关性近似表示为：
{y}_{{\mathrm{H}}}\left(x\right)=\alpha {F}_{{\mathrm{l}}}({x}_{{\mathrm{H}}},{y}_{\rm{L}})+(1-\alpha ){F}_{{\mathrm{nl}}}({x}_{{\mathrm{H}}},{y}_{{\mathrm{L}}}) (2) 式中： {F}_{{\mathrm{l}}}({x}_{{\mathrm{H}}},{y}_{{\mathrm{L}}}) 表示高精度数据与低精度数据之间的线性相关性； {F}_{{\mathrm{nl}}}({x}_{{\mathrm{H}}},{y}_{{\mathrm{L}}}) 表示高精度数据与低精度数据之间的非线性相关性； \alpha 为超参数，用来调节线性相关性与非线性相关性之间的比重。
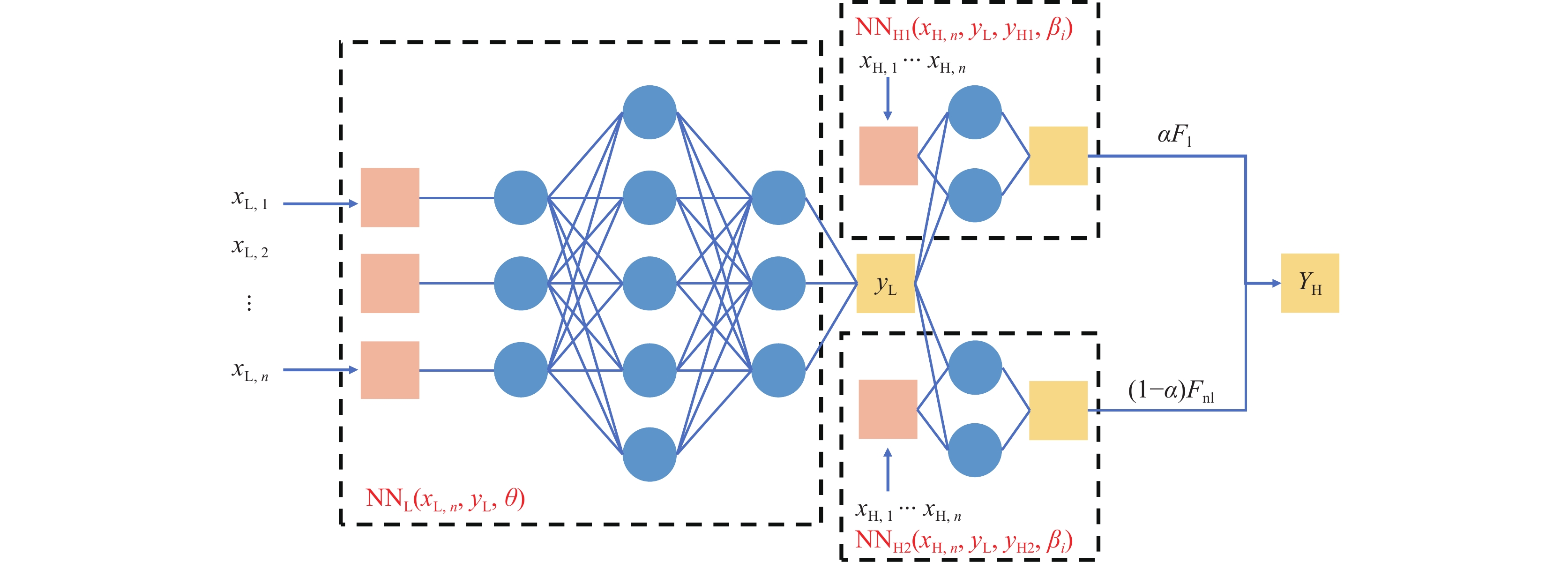
多精度神经网络复合模型如图7所示。该复合模型由3个深度神经网络构成，其中 {x}_{{\mathrm{L}},n} 与 {y}_{{\mathrm{L}}} 代表低精度数据， {x}_{{\mathrm{H}},n} 与 {y}_{{\mathrm{H}}} 代表高精度数据， n 代表设计变量的维度。第一个模型 {{\mathrm{NN}}}_{{\mathrm{L}}}({x}_{\mathrm{{L}},n},{y}_{{\mathrm{L}}},\theta ) 使用低精度数据进行训练，用来学习低精度条件下目标函数的数据特征以及变化趋势；第二个模型 {{\mathrm{NN}}}_{{\mathrm{H}}1}({x}_{{\mathrm{H,n}}},{y}_{{\mathrm{L}}},{y}_{{\mathrm{H}}1}) 中不包含激活函数，用来学习低精度数据与高精度数据之间的线性相关性；第三个模型 {{\mathrm{NN}}}_{{\mathrm{H}}2}({x}_{{\mathrm{H,n}}},{y}_{{\mathrm{L}}},{y}_{{\mathrm{H}}2}) 可以学习低精度数据与高精度数据之间的非线性相关性。结合低精度条件下，所获取的目标函数的变化趋势以及低精度数据和高精度数据之间的相关性，可以基于少量高精度数据构建出目标函数的模型。
上述复合模型中，超参数 \theta 与 {\beta }_{i} 是神经网络的权值和偏差，可以通过优化损失函数来对 \theta 与 {\beta }_{i} 进行训练。
2.2 数值算例验证
在本小节中，分别使用多精度神经网络与深度神经网络来对某一维不连续函数进行拟合，通过对比拟合结果，验证MFDNN模型的拟合能力。其中低精度数据 {y}_{\rm{L}} 与高精度数据 {y}_{\rm{H}} 分别由式（3）与式（4）给出：
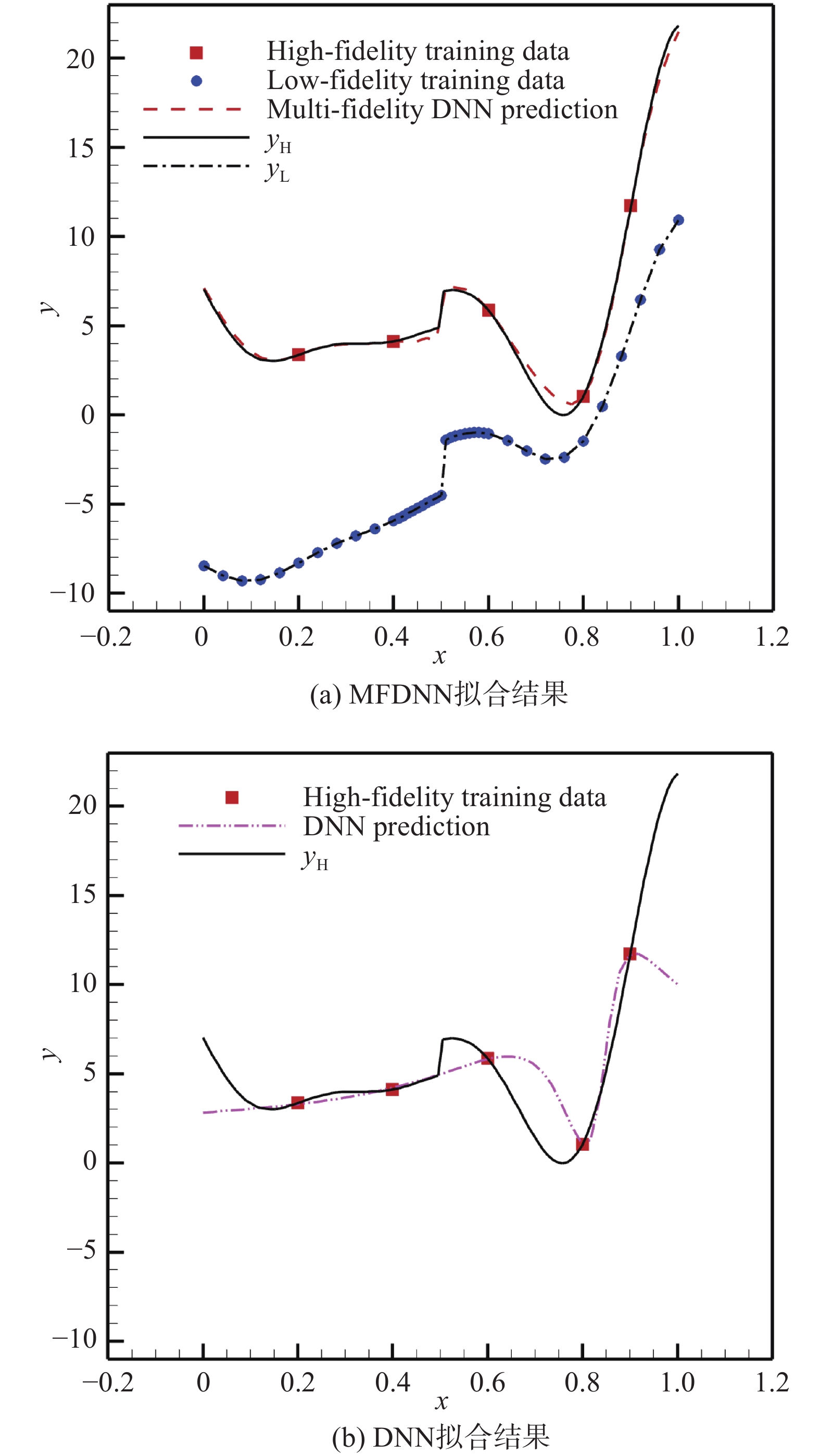
{y}_{\rm{L}}=\left\{\begin{array}{c}0.5{\left(6x-2\right)}^{2}{\sin}\left(12x-4\right)+10\left(x-0.5\right)-5,\\ 0\le x\le 0.5\\ 0.5{\left(6x-2\right)}^{2}{\sin}\left(12x-4\right)+10\left(x-0.5\right)-2,\\ 0.5 < x\le 1\end{array}\right. (3) {y}_{\rm{H}}=\left\{\begin{array}{c}2{y}_{\rm{L}}\left(x\right)-20x+20, \;0\le x\le 0.5\\ 2{y}_{\rm{L}}\left(x\right)-20x+24, \;0.5 < x\le 1\end{array}\right. (4) 对于MFDNN模型，基于5个高精度样本点与41个低精度样本点对其进行训练；对于DNN模型，仅基于5个高精度样本点对其进行训练。拟合结果如图8所示。
由图8可以看出，尽管在 0.4 < x < 0.6 内没有高精度数据用来建模，但是MFDNN模型可以较好地拟合不连续点 x=0.5 处的高精度数据， DNN模型在此处则拟合较差。这是因为在 0.4 < x < 0.6 范围内，高精度数据与低精度数据具有相近的趋势，MFDNN模型可以通过低精度模型 {{\mathrm{NN}}}_{\rm{L}} 对该趋势进行捕捉并加以学习，然后基于所建立的神经网络模型 {{\mathrm{NN}}}_{{\mathrm{H}}1} 与 {{\mathrm{NN}}}_{{\mathrm{H}}2} 获得低精度数据与高精度数据之间的相关性。使用这3个模型所获得的信息，可以实现对高精度数据的精准预测。该算例结果表明，在使用相同数量高精度数据点的条件下，MFDNN模型的学习能力更强，可以更精准地拟合实际函数。
2.3 MFDNN模型的构建
MFDNN模型的建立依赖于不同精度的数据。首先，采用数值模拟的手段，利用粗网格低阶精度的汽车气动仿真数据（基于Euler方程），学习基本的物理特征和设计空间内的基本变化规律；在此基础上，通过加入少量的细网格高阶精度汽车气动评估数据（基于N-S方程），来构建基于MFDNN的汽车气动力模型，实现多源气动数据融合建模与对目标气动特性的精准评估。
其中，低精度数据能够正确指导优化的前提是其与高精度数据具有相近的趋势，随机抽取10个工况进行验证，结果如图9所示。
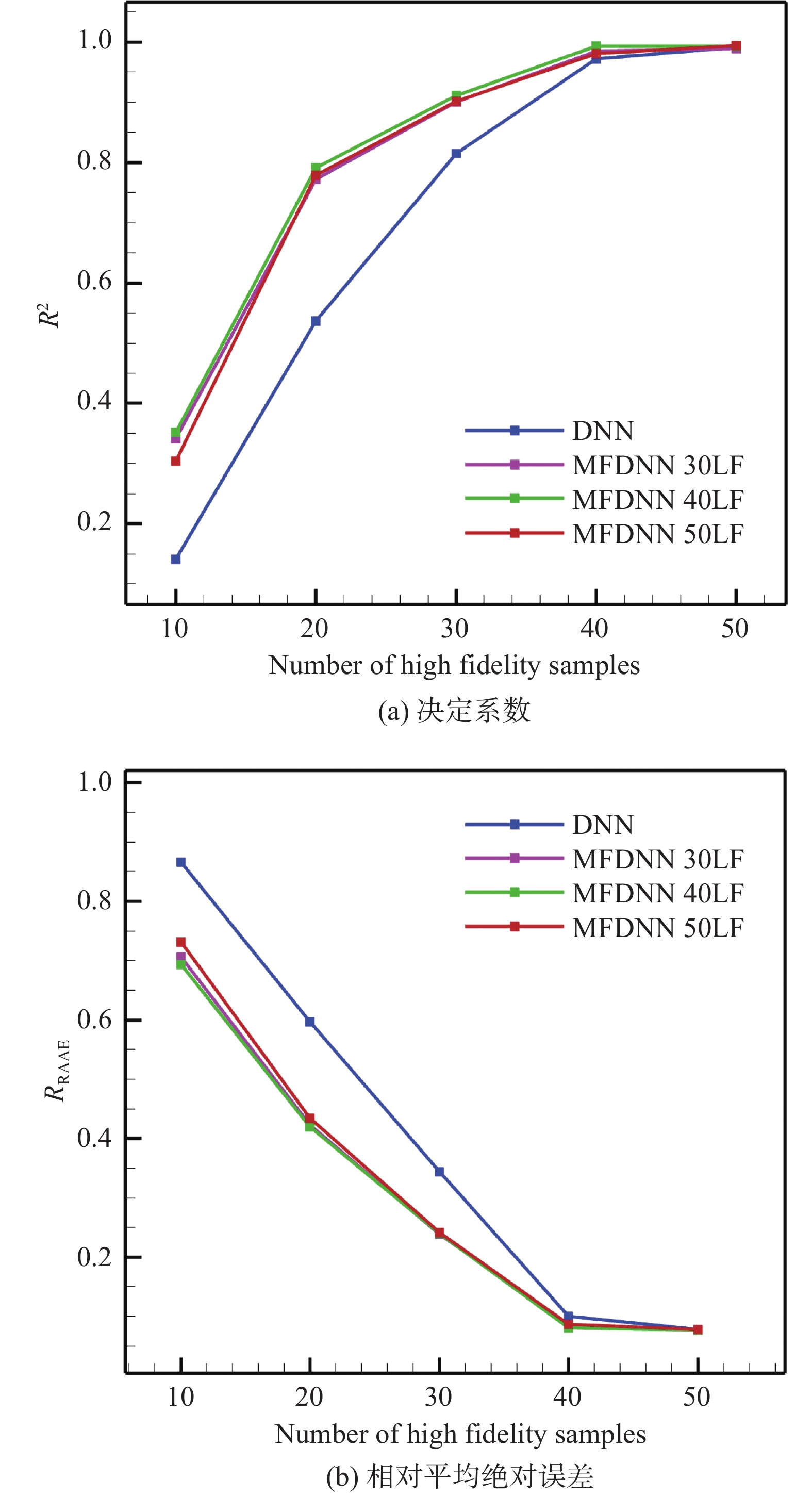
为了验证多精度数据融合建模精度的优势，将多精度与单精度气动力模型建模精度进行了对比。使用决定系数和相对平均绝对误差作为模型准确性的评估指标。其中决定系数 {R}^{2} 与相对平均绝对误差 R_{{\mathrm{RAAE}}} 如下所示：
{R}^{2}=1-\frac{\displaystyle{\sum }_{i=1}^{M}{({f}\left({x}_{i}\right)-f({x}_{i}\left)\right)}^{2}}{\displaystyle{\sum }_{i=1}^{M}{({f}\left({x}_{i}\right)-\overline{{f}\left({x}_{i}\right)})}^{2}} (5) R_{\mathrm{RAAE}}=\frac{\dfrac{1}{M}\displaystyle{\sum }_{i=1}^{M}\left|{f}\left({x}_{i}\right)-f\left({x}_{i}\right)\right|}{\sqrt{\dfrac{1}{M}\displaystyle{\sum }_{i=1}^{M}{({f}\left({x}_{i}\right)-\overline{{f}\left({x}_{i}\right)})}^{2}}} (6) 在测试集中使用了50个高可信度样本来验证模型的准确性。图10显示了在不同样本组合下，决定系数和相对平均绝对误差相对于高精度样本数量的变化，其中LF为低精度数据。可以看到，高精度样本数量越少时，多精度气动力模型精度相对于单精度气动力模型精度的提高就越大，且多精度气动力模型在不同样本组合下的精度均明显优于单精度气动力模型。
2.4 不同优化框架结果对比与分析：
本节分别使用基于MFDNN的在线优化框架以及基于DNN的在线/离线优化框架对MIRA模型进行气动减阻优化设计，以验证基于MFDNN在线优化框架的优越性。
要建立MFDNN与DNN模型，首先要获取初始样本点。本文通过拉丁超立方抽样法在整个设计空间内进行均匀取样，由于设计变量共有10个，故选取10n个高精度数据，即100个高精度数据作为高精度数据初始样本点。为了能大致反映出整个设计空间内的目标函数的数据特征以及变化趋势，选取的低精度点不能过少，本文共计选择了30、40、50个低精度数据作为低精度数据初始样本点。对于基于MFDNN模型的汽车气动外形优化设计框架，分别选取30、40、50个低精度样本点与5个高精度样本点对MFDNN模型进行训练，基于所建立的模型，进行在线优化。对于基于DNN模型的汽车气动外形优化设计框架，由于低精度数据的可靠性较低，仅用低精度数据对DNN模型进行训练时，模型拟合结果较差，因此仅采用高精度点进行训练，同时，也可以与MFDNN模型相区分。分别选取5、20、50、100个高精度样本点对DNN模型进行训练，然后基于所训练的DNN模型进行在线与离线优化。其中，在线优化指的是每进行一次迭代，训练代理模型的样本点都进行更新，在原有样本点的基础上，加入上次迭代所获得的最优结果，从而实现对代理模型的更新，通过迭代逼近最优；离线优化指的是使用优化算法对代理模型进行单次优化以获取最优结果。
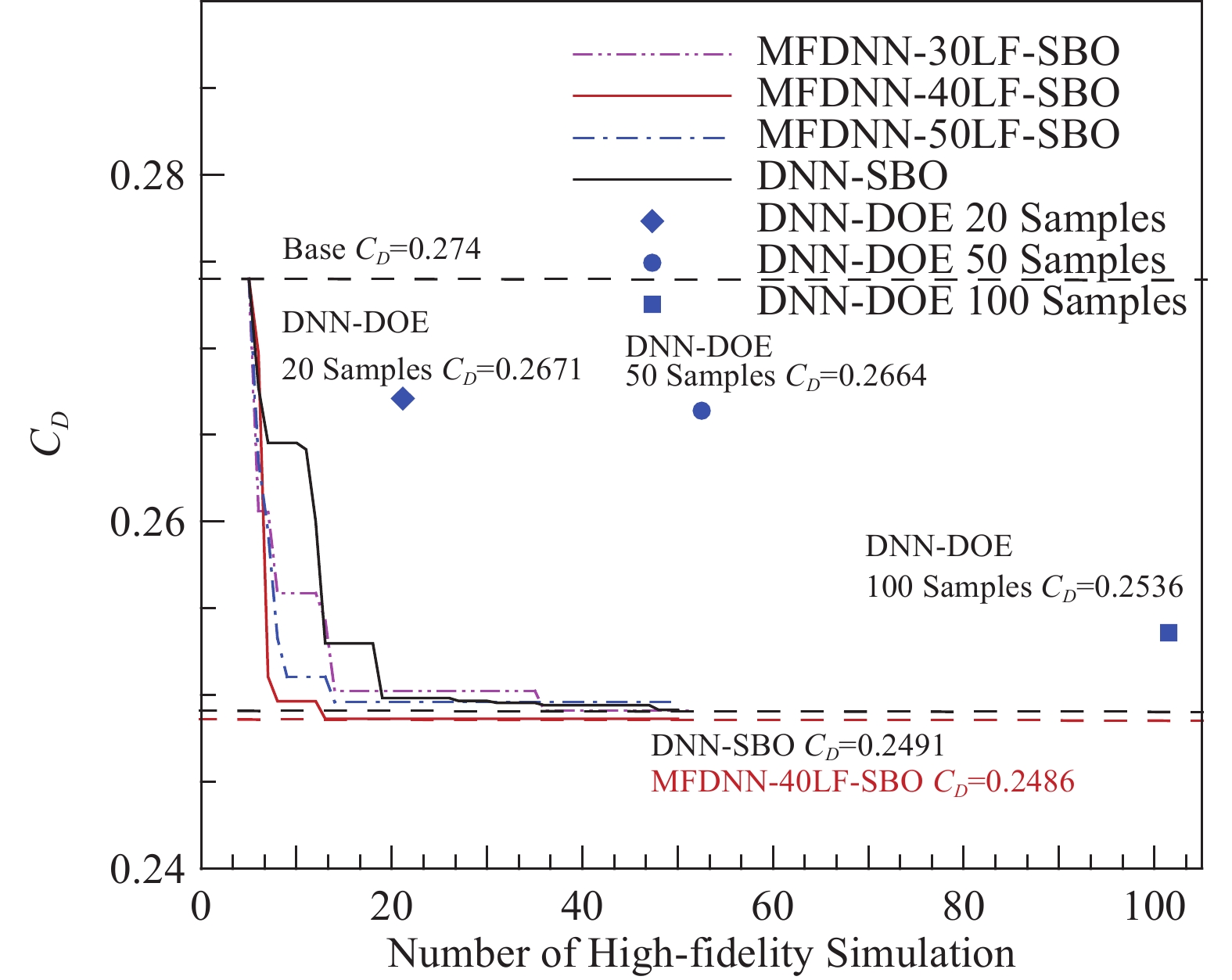
几种不同的优化框架下的收敛曲线如图11所示，部分结果在表5中展示。其中MFDNN online opt为基于MFDNN的在线优化框架，DNN online opt为基于DNN的在线优化框架，DNN offline opt为基于DNN的离线优化框架。
![]()
图 11 几种不同优化框架结果对比Figure 11. Comparison of results of several different optimization frameworks表 5 优化结果对比Table 5. Comparison of optimization results{C}_{D} {\Delta C}_{D}/{C}_{D} 收敛所需高
精度点/个收敛
用时/hMFDNN online 30LF opt 0.2496 8.91% 37 69.80 MFDNN online 40LF opt 0.2486 9.27% 14 29.74 MFDNN online 50LF opt 0.2523 7.92% 15 35.00 DNN online opt 0.2491 9.08% 49 83.65 20 Samples DNN offline opt 0.2671 2.52% 20 34.85 50 Samples DNN offline opt 0.2664 2.77% 50 87.13 100 Samples DNN offline opt 0.2536 7.45% 100 174.27 在取得相近或更优优化结果的前提下，以收敛用时作为收敛速度的评判标准，基于MFDNN的优化框架的收敛速度是基于DNN的离线优化框架的5.85倍，是基于DNN的在线优化框架的2.81倍，可以看到，多精度气动优化设计方法相较于单精度气动优化设计方法极大程度提升了优化效率，降低了优化成本。
需要注意的是，低精度样本并非越多越好。由图10与表5可知，融合了50个低精度样本数据的多精度气动力模型拟合精度反而低于融合了40个低精度样本的多精度气动力模型，基于50个低精度样本的MFDNN的优化框架优化效率也要差于基于40个低精度样本的MFDNN的优化框架优化效率。这是因为过多的低精度数据会导致低精度数据特征掩盖高精度数据特征，导致低精度样本与高精度样本之间的相关性难以被准确获得；且在整个设计空间内，低精度数据的变化趋势也不可能与高精度数据的变化特征完全相同，小部分低精度数据会提供错误的信息。
对基于融合了40个低精度样本的MFDNN的在线优化框架所得到的优化结果进行分析，优化前后中心对称面轮廓对比如图12所示。
![]()
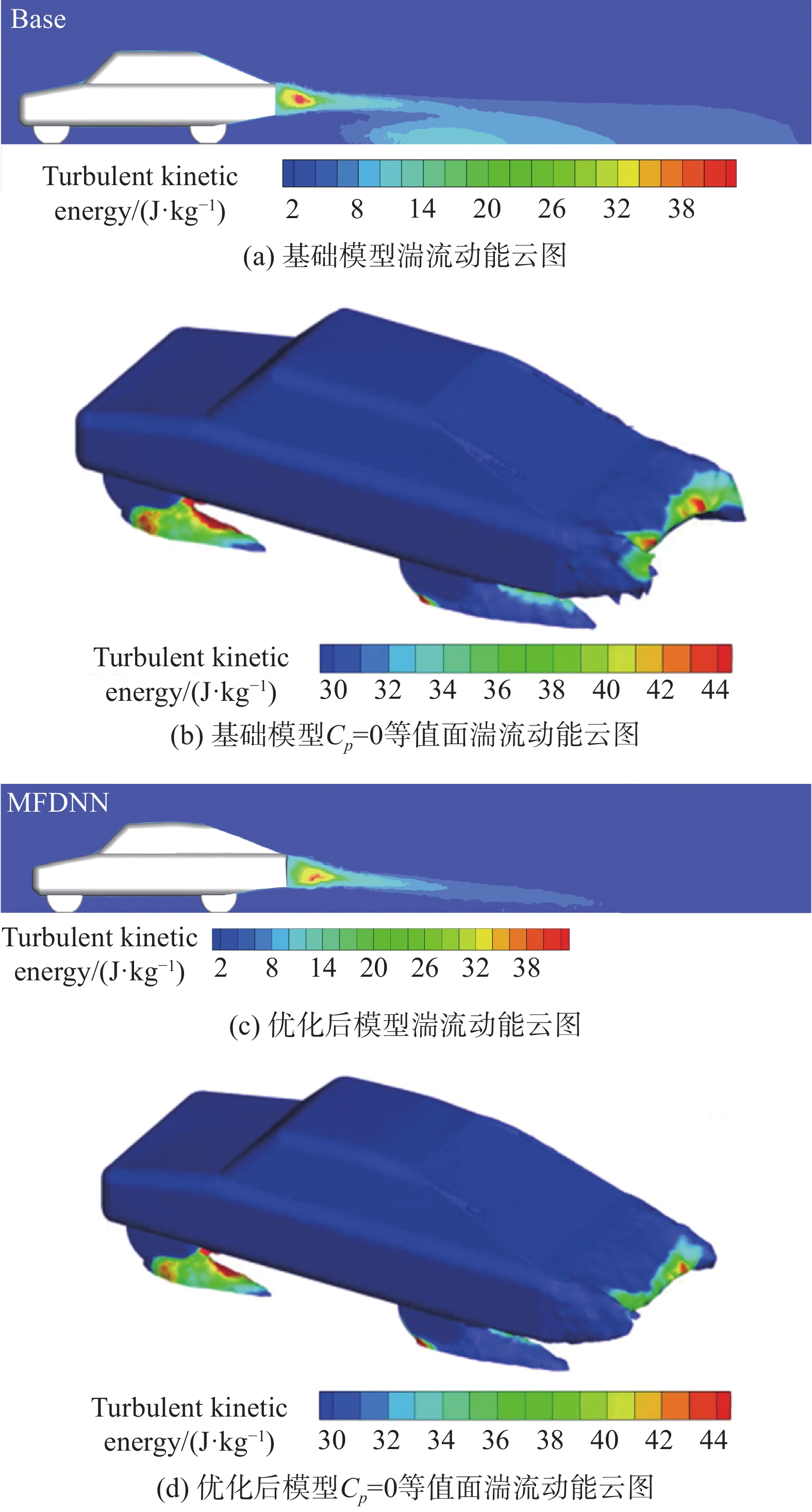
图 12 优化前后中心对称面轮廓对比Figure 12. Comparison of central symmetric surface contour before and after optimization优化前后湍流动能云图与压力云图分别如图13、14所示。汽车尾部湍流区是能量耗散的主要区域，对汽车的气动特性有重要影响。由图13可知，优化后汽车尾部的湍流区面积明显减小。经测量，优化前尾部区域湍流动能最大值为42.95 J/kg，优化后尾部湍流动能最大值为40.02 J/kg，湍流极值降低，湍流情况得到了改善，有助于减少能量耗散，降低汽车所受到的气动阻力。
![]()
图 13 优化前后湍流动能云图对比Figure 13. Comparison of turbulent kinetic energy contours before and after optimization![]()
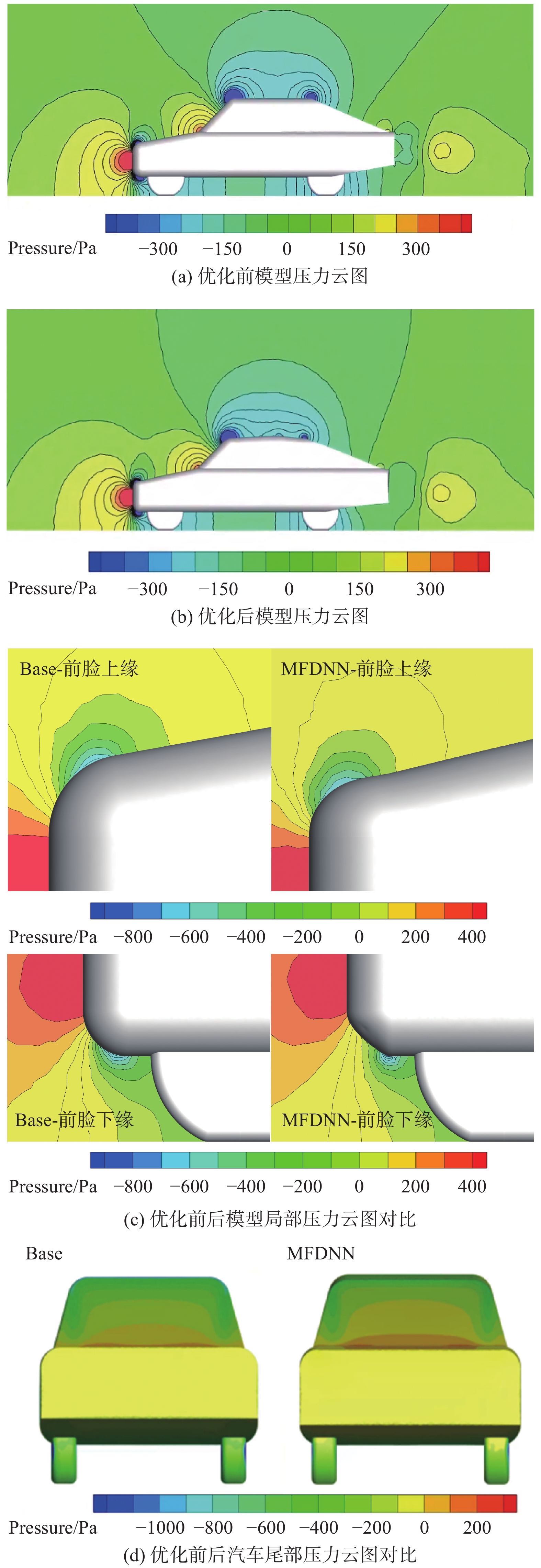
图 14 优化前后压力云图对比Figure 14. Comparison of pressure contours before and after optimization观察图14中优化前后的压力云图可以发现前风窗、后风窗、前脸上缘处的压力梯度均有明显的降低，压力梯度的降低意味着更小的空气速度变化率，有助于减小汽车受到的剪切摩擦力，同时可以抑制湍流的生成，改善气流的分离现象，这有利于降低能量损耗与汽车受到的阻力。观察到汽车前脸下缘的压力梯度未有明显改善，推测是由于参数化时，网格变形范围较小造成的。通过观察图14（d）还可以发现，优化后汽车尾部的负压区域明显减小，正压区明显增加，这有利于减小汽车行驶时的前后压差阻力。
结合图13和图14可以清楚地看到，本文提出的这种基于MFDNN的在线优化框架能够有效提升汽车的气动特性。与单精度优化框架相比，基于MFDNN的在线优化框架能够充分融合不同精度数据中所包含的知识，在优化过程中展现出更好的优化效果，并且可以使用更少的高精度样本点来实现收敛。
3. 结 论
本文以改善汽车空气动力学性能为目标，对MIRA模型进行了气动外形优化设计。同时，为解决现有气动外形优化方法中高精度代理模型构建较为困难的问题，发展了一种基于多精度深度神经网络的汽车气动外形优化方法，能够充分利用不同精度数据中所包含的有用信息，有效降低了高精度气动力模型对高精度CFD数据的依赖性，实现了小样本条件下对目标气动特性的精准评估，有效降低了气动力建模成本，提升了优化效率。经MIRA模型验证，在达到相近优化效果的前提下，本文所发展的基于多精度深度神经网络的优化方法的收敛速度是基于单精度深度神经网络优化方法的2.81倍。该方法有效降低了汽车气动外形优化设计中所需的高精度数据点个数，达到了降本增效的目的。
但需要注意的是，本文在对MIRA模型进行气动优化时，没有施加约束条件。这种局限性可能会导致优化结果在可行性方面存在不足。此外，本文对于优化变量的选择是基于研究人员对流场的分析而选取的，这种选择存在一定的主观性。未来的研究应进一步探讨如何在优化过程中引入更多约束条件，以及如何更客观地确定优化变量，以提高优化结果的可靠性。
-
![]()
图 4 基础模型压力云图与湍流动能云图
Figure 4. Contours of the pressure and turbulent kinetic energy of the basic model
![]()
图 6 基于多精度神经网络模型的优化框架
Figure 6. Optimization framework based on multi-fidelity neural network model
![]()
图 11 几种不同优化框架结果对比
Figure 11. Comparison of results of several different optimization frameworks
![]()
图 12 优化前后中心对称面轮廓对比
Figure 12. Comparison of central symmetric surface contour before and after optimization
![]()
图 13 优化前后湍流动能云图对比
Figure 13. Comparison of turbulent kinetic energy contours before and after optimization
![]()
图 14 优化前后压力云图对比
Figure 14. Comparison of pressure contours before and after optimization
表 1 模型基本尺寸表[14]
Table 1 Quick-back MIRA geometry
序号 名称 尺寸/mm 1 车长 4165 2 车宽 1625 3 车高 1421 4 轴距 2540 5 轮距 1270 6 离地间隙 205 7 轮胎半径 305 8 轮胎宽 180 
下载: 导出CSV
表 2 求解格式设置
Table 2 Computational settings
高精度数据 低精度数据 网格量 4788261 795757 迎风格式 二阶 一阶 求解方程 N-S Euler 湍流模型 k{\text{-}}\varepsilon 模型 迭代次数 1300 550 数值模拟耗时 1.74 h 0.18 h 注：使用CPU为32 cores Inter Xeons Golden 6226R 2.9 GHz
下载: 导出CSV
表 3 不同网格量下数值仿真所得到的阻力系数
Table 3 Resistance coefficients obtained by numerical simulations using different mesh sizes
体网格数目 {C}_{D} 验证计算 284万 0.285 348万 0.279 480万 0.274 512万 0.274 风洞数据[15] 0.278
下载: 导出CSV
表 4 所选取的设计变量的上下限
Table 4 The upper and lower bounds of the selected design variables
设计变量 {x}_{i} 变形范围/m 接近角z方向 [–0.015, 0.025] 发动机罩前缘z方向 [–0.04, 0.05] 前风窗y方向 [–0.01, 0.02] 前风窗z方向 [–0.01, 0.02] 后风窗y方向 [–0.03, 0.03] 后风窗z方向 [–0.04, 0.05] 后备箱盖y方向 [–0.04, 0.05] 后备箱盖z方向 [–0.04, 0.05] 离去角y方向 [–0.03, 0.03] 离去角z方向 [–0.05, 0.05]
下载: 导出CSV
表 5 优化结果对比
Table 5 Comparison of optimization results
{C}_{D} {\Delta C}_{D}/{C}_{D} 收敛所需高
精度点/个收敛
用时/hMFDNN online 30LF opt 0.2496 8.91% 37 69.80 MFDNN online 40LF opt 0.2486 9.27% 14 29.74 MFDNN online 50LF opt 0.2523 7.92% 15 35.00 DNN online opt 0.2491 9.08% 49 83.65 20 Samples DNN offline opt 0.2671 2.52% 20 34.85 50 Samples DNN offline opt 0.2664 2.77% 50 87.13 100 Samples DNN offline opt 0.2536 7.45% 100 174.27
下载: 导出CSV
-
[1] FORRESTER A I J, KEANE A J . Recent advances in surrogate-based optimization[J]. Progress in Aerospace Sciences,2009 ,45 (1-3 ):50 −79 . doi: 10.1016/j.paerosci.2008.11.001[2] 张英朝, 薛学栋, 丁伟, 等 . 某两厢车气动外形减阻自动优化设计[J]. 同济大学学报(自然科学版),2016 ,44 (11 ):1771 −1775, 1795 .ZHANG Y C, XUE X D, DING W, et al . Automatic shape optimization of hatchback to reduce aerodynamic drag[J]. Journal of Tongji University (Natural Science),2016 ,44 (11 ):1771 −1775, 1795 (in Chinese).[3] 赖晨光, 段孟华, 陈小雄, 等. 基于智能算法的汽车气动外形参数多目标优化[J]. 北京工业大学学报, 2017, 43(9): 1320−1327. LAI C G, DUAN M H, CHEN X X, et al. Multi-objective optimization of vehicle aerodynamic shape parameters based on an intelligent algorithm[J]. Journal of Beijing University of Technology, 2017, 43(9): 1320−1327(in Chinese).
[4] 张英朝, 薛学栋, 丁伟, 等. 某两厢车气动外形减阻自动优化设计[J]. 同济大学学报(自然科学版), 2016, 44(11): 1771−1775, 1795. ZHANG Y C, XUE X D, DING W, et al. Automatic shape optimization of hatchback to reduce aerodynamic drag[J]. Journal of Tongji University (Natural Science), 2016, 44(11): 1771−1775, 1795(in Chinese).
[5] HAN Z H, ZIMMERMANN, GÖRTZ S. Alternative cokriging method for variable-fidelity surrogate modeling[J]. AIAA Journal, 2012, 50(5): 1205−1210.
[6] HAN Z H, GÖRTZ S. Hierarchical Kriging model for variable-fidelity surrogate modeling[J]. AIAA Journal, 2012, 50(9): 1885−1896.
[7] BONFIGLIO L, PERDIKARIS P, BRIZZOLARA S, et al. Multi-fidelity optimization of super-cavitating hydrofoils[J]. Computer Methods in Applied Mechanics and Engineering, 2018, 332: 63−85.
[8] ZHENG H Y, XIE F F, JI T W, et al . Multifidelity kinematic parameter optimization of a flapping airfoil[J]. Physical Review E,2020 ,101 (1-1 ):013107 . doi: 10.1103/PhysRevE.101.013107[9] DING F, KAREEM A. A multi-fidelity shape optimization via surrogate modeling for civil structures[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 178: 49−56.
[10] ZHANG Y, HAN Z H, ZHANG K S. Variable-fidelity expected improvement method for efficient global optimization of expensive functions[J]. Structural and Multidisciplinary Optimization, 2018, 58(4): 1431−1451.
[11] ZHANG X S, XIE F F, JI T W, et al. Multi-fidelity deep neural network surrogate model for aerodynamic shape optimization[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 373: 113485.
[12] HAN Z H, XU C Z, ZHANG L, et al. Efficient aerodynamic shape optimization using variable-fidelity surrogate models and multilevel computational grids[J]. Chinese Journal of Aeronautics, 2020, 33(1): 31−47.
[13] KOU J Q, NING C J, ZHANG W W. Transfer learning for flow reconstruction based on multifidelity data[J]. AIAA Journal, 2022, 60(10): 5821−5842.
[14] HOFFMAN J, MARTINDALE B, ARNETTE S, et al. Effect of test section configuration on aerodynamic drag measurements[J]. SAE Transactions, 2001, 110: 680−694.
[15] 谷正气, 王师, 仇健, 等. MIRA模型组尾部造型风洞试验研究[J]. 科技导报, 2011, 29(8): 67−71. GU Z Q, WANG S, QIU J, et al. Wind tunnel tests of MIRA model group for study of vehicle's rear shape[J]. Science and Technology Review, 2011, 29(8): 67−71(in Chinese).
[16] MENG X H, KARNIADAKIS G E. A composite neural network that learns from multi-fidelity data: Application to function approximation and inverse PDE problems[J]. Journal of Computational Physics, 2020, 401: 109020.
计量
- 文章访问数: 829
- HTML全文浏览量: 26
- PDF下载量: 36
