0.   引　言

在航空领域中，沟槽是一种重要的减阻结构，在A340-300机翼上的应用中可以减小8.2%的摩擦阻力，但布置在机翼前缘和起落架附近的沟槽结构容易被灰尘侵蚀，使沟槽结构失去减阻效应。为了防止沟槽被灰尘侵蚀^[1]，提高沟槽的抗污染能力，在沟槽表面布置疏水材料可以兼顾沟槽的减阻特性和抗污染能力^[2-3]。

疏水材料作为一种抗污染^[2-3]、自清洁^[4-5]、抗菌防腐^[5-6]的重要材料形式，近年来得到广泛的研究。疏水材料的常见结构包括倒金字塔结构^[7]、柱状结构^[8-9]、纳米针结构等^[10]，这些微结构可简化称之为一类凹坑微结构。疏水材料中的疏水结构量级从微米到纳米量级不等^[11]。在研究疏水材料疏水特性的同时，认识和预测疏水材料对壁面流动的影响关系到微结构（如上述沟槽）的减阻特性。大量研究表明可以采用一种滑移速度特性计入疏水材料对近壁区的流动影响。然而，对于微米级流动，尚可以通过Navier-Stokes（N-S）方程求解，但对于纳米级的流动，连续性假设的失效导致N-S方程无法描述疏水结构内的流动，需要采用介观甚至微观尺度的分析方法。

关于疏水材料的滑移特性，目前人们主要关注微结构在液体下的滑移特性，主要通过实验和数值模拟手段进行研究。Li等^[12]和Wang等^[13]通过在水和去离子水中实验，得到纳米级疏水材料的滑移长度为纳米级的结论，并发现溶解于液体的气泡能大幅增加滑移长度。Guo等^[14]对微米级疏水材料进行了实验研究，发现不同高度的疏水结构和不同类别的实验液体会影响滑移长度，这些微米级的疏水材料滑移长度在微米级。Lee等^[11]在研究纳米级疏水材料和微米级疏水材料的基础上还研究了分层结构（包含微米级和纳米级）的疏水材料，研究表明，在实验流体是液体的条件下，相较于微米级结构，分层结构上的滑移长度有所增加，但如果微米级结构的固体分数小于10%，分层结构反而会使滑移长度减小。Jin等^[15]和周健壮^[16]通过分子动力学（Molecular dynamics, MD）方法分析纳米狭缝间的滑移流动，对于1～3 nm狭缝，滑移长度在0.3～1 nm，远小于实验结果。Jin等^[15]认为这是没有考虑单相水中溶解的气体导致的，纳米气泡可能会显著增加疏水材料的滑移长度。周健壮^[16]还通过去除光滑纳米狭缝表面的原子来研究粗糙度对滑移长度的影响，研究发现表面粗糙度对滑移长度产生了负面影响。

针对滑移边界的许多研究表明，滑移速度能够有效减小阻力。Mohammad等^[17]与Fuaad等^[18]通过研究摩擦雷诺数为180的槽道流发现，滑移长度大于1×10^–5 m时，摩擦阻力减小28%以上。而且，相对于脊状疏水表面，柱状超疏水表面摩擦阻力的减阻效果最好，在湍流中减阻率达到约22%。Li等^[19]对雷诺数为1～180带滑移速度边界的圆柱绕流进行了数值研究，以特征长度无量纲化，当滑移长度达到特征长度的0.01倍时有明显的减阻效果。Alireza等^[20]通过MD对纳米通道中的水流进行模拟，纳米通道中排列有纳米柱状结构，发现随着纳米柱面积占比的减小，纳米柱的摩擦系数减小，滑移长度增加，且交错排列的摩擦系数比对齐排列的摩擦系数高。Niu等^[21]对水下航行器模型表面采用滑移速度模型，研究表明超疏水表面可以降低表面的湍流波动压力和边界层速度，还会影响壁面剪切应力的大小，进而影响近壁面湍流的状态，这样就改变了涡的形成和脱落。从上述研究结果可以看出，疏水微结构的差异对减阻性能有重要影响。

在大气环境下，目前高Kn数的问题主要围绕高速、高空环境下展开的。Ehsan等^[22]通过直接模拟蒙特卡罗（direct simulation Monte Carlo, DSMC）方法研究热流驱动的空腔在滑移流和过渡流区中的热行为，发现，增加克努森数，温度梯度减小，热蠕变引起沿侧壁的切向速度，该切向速度随着克努森数的降低而减弱。Mommadzadeh等^[23]通过DSMC方法研究了低速下滑移流和过渡流下的微/纳米腔中的熵行为和热通量，结果表明，克努森数的增加使流动沿着空腔的水平中心线经历更大的温度变化，同时，热通量分布的曲率减小，但该研究没有重点关注其中的流动特性。Guo等^[24]通过DSMC方法研究了高速气体在不同长深比和来流条件下的空腔流场特性，发现当自由流从连续流型向过渡流型转变时，来流马赫数对空腔流动特性的影响逐渐减弱：对于连续流和滑移流，来流马赫数的变化具有改变空腔内再循环区域的能力。然而，对于过渡流，腔内的再循环区看起来没有明显变化。Paolicchi等^[25]通过DSMC方法研究了稀薄气体下的高速空腔流动，研究了长深比对流场结构和气动表面量的影响。Jiang等^[26]通过DSMC方法研究了空腔形状和尺寸对稀薄高速流动的影响。

综上所述，对于低空低速下航空领域微结构的疏水材料对减阻的影响特性还需要进一步明晰。亚声速民机表面的沟槽暴露于空气中，其作为大尺寸疏水结构^[1]，与小尺寸疏水材料结构叠加的分层结构有望提升壁面的滑移长度^[11]，同时提高沟槽的防污能力。为了探索低速环境下空气中纳米级疏水材料的滑移特性，为沟槽表面叠加小尺寸疏水材料设计提供思路和参考，本文采用离散统一气体动理学格式^[27-28]（discrete unified gas-kinetic scheme, DUGKS）对不同尺寸变化下的二维低速凹坑流滑移特性进行研究，以期揭示微结构尺寸对滑移速度的影响规律。

1.   计算方法及模型验证

DUGKS方法由华中科技大学郭照立教授及香港科技大学徐昆教授提出，结合了UGKS 胜任全流域及格子玻尔兹曼方法操作简易的优势。DUGKS 的主要特点是在分布函数输运方程及界面重构中耦合了粒子输运及碰撞，并通过引入辅助函数移除了隐式碰撞项，因此其计算参数无需分辨流场特征参数 Kn，在全 Kn 流域能提供满意且经济可行的物理解。该方法在连续流域优于传统的有限体积格子Boltzmann方法（finite volume lattice Boltzmann method, FVLBM），相比于传统的稀薄流数值模拟方法DSMC更适合非定常流动。DUGKS是基于Bhatnagar-Gross-Krook（BGK）碰撞模型的Boltzmann方程发展起来的全流域流动数值预测方法。由于BGK模型只使用一个单一的松弛时间，这导致固定的Pr = 1，为了克服这一问题，采用BGK-Shakhov模型。在N维空间，BGK-Shakhov模型表示为：

其中，f = f(x,$\xi$,η,$\zeta$.τ)是速度分布函数，x是空间坐标，$\xi$是速度离散空间，η是分子转动变量，$\zeta$是自由度变量，τ是松弛时间，与动力黏性系数μ和压强p有关，τ = μ/p；f ^s是Shakhov平衡分布函数：

其中：c是相对速度，$c = \xi -u$，u是宏观流速；f ^eq是麦克斯韦平衡分布函数：

式中：R是气体常数，T是温度。

流场变量通过守恒形式表示：

式中： ρE = ρu²/2+ρe是总能量，ψ = (1, $\xi$, $\xi$²+η²+$\zeta$²)是碰撞不变量，其中e = c_vT是内能，c_v是固定体积的比热容，c_p是固定压强的比热容，且c_v = (3+K)R/2，c_p = (5+K)R/2，因此比热比为:

式中，对于单原子分子，K = 0，对于双原子分子K = 1，本文气体为双原子分子。

压强由理想气体状态方程 p = ρRT 得出，热流由式（6）给出:

动力黏度μ通过硬球（HS）模型或变径硬球（VHS）模型得到:

其中：μ_ref是在温度T_ref下的黏性系数，ω是与HS模型或VHS模型相关的常数。

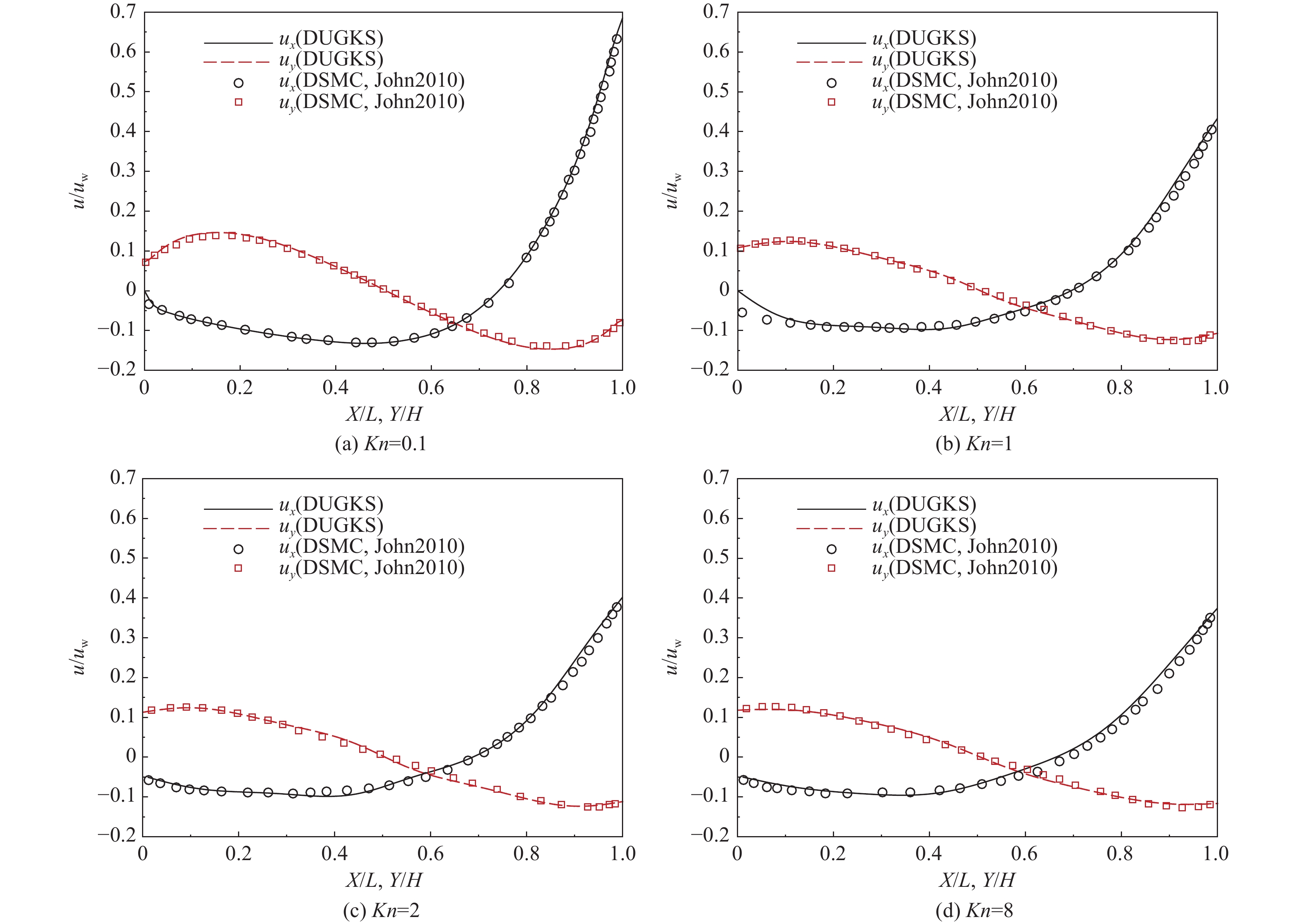
为验证数值方法的可行性，对Kn = 0.1～8的微腔流进行计算。顶壁速度${{{u_w}} \mathord{\left/ {\vphantom {{{u_w}} {\sqrt {\gamma RT} }}} \right. } {\sqrt {\gamma RT} }}$ = 0.16，采用Gauss-Hermite求积规则确定离散速度和权重，高斯点为24×24，物理网格点为80×80，采用HS模型，ω = 0.5，对于所有情况，CFL（Courant-Friedrichs-Lewy）设置为0.25。图1显示了不同Kn下的速度分布，并与John等^[29]的DSMC数据进行对比。结果表明，DUGKS结果与DSMC结果在滑移流与过渡流范围内皆符合较好。

图  1  不同Kn下空腔中心速度分布度分布

Figure  1.  Velocity profiles at the cavity center under different Kn

下载: 全尺寸图片 幻灯片

2.   计算模型

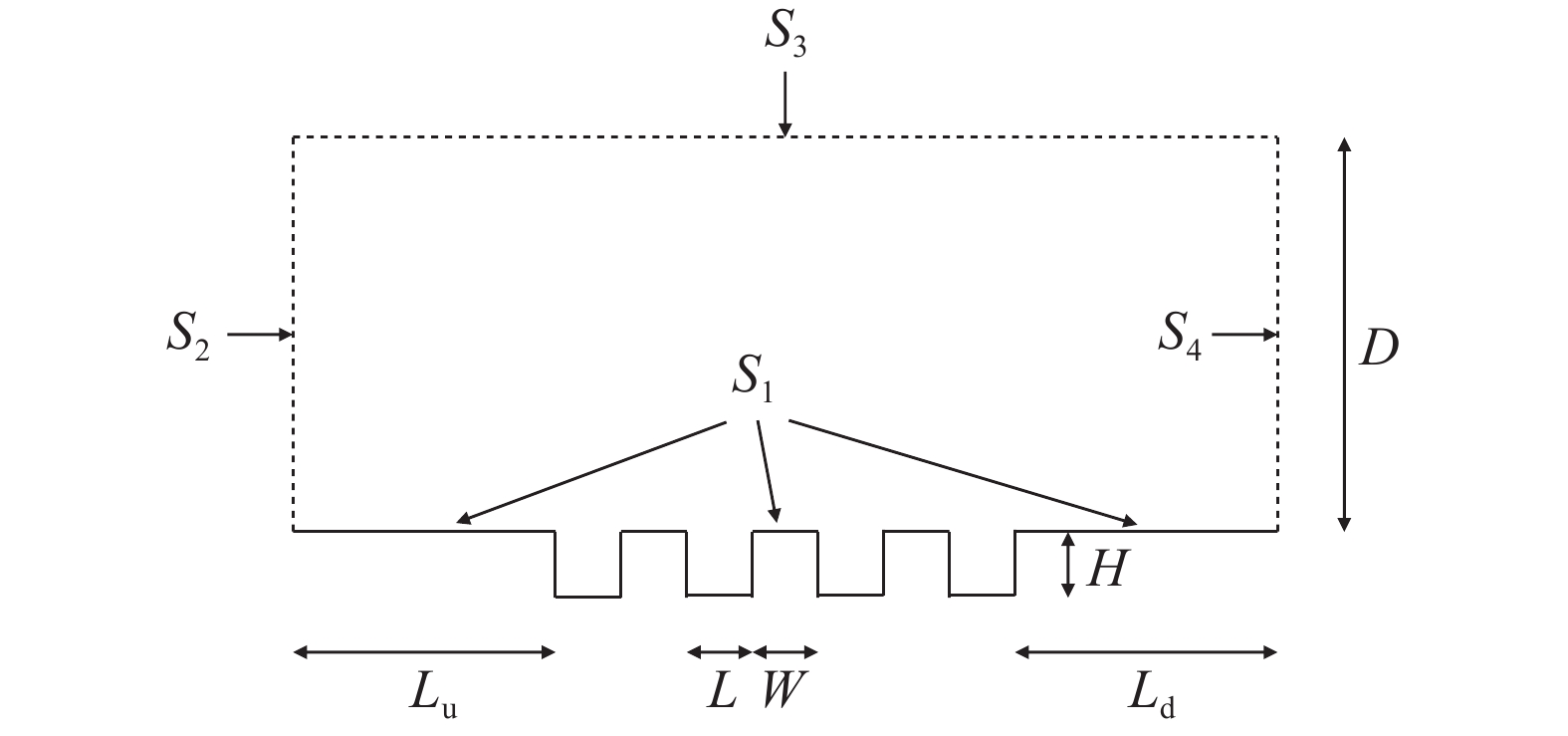
图2为空腔流动的计算域示意图，四个空腔按照固定间隔w排列，空腔的宽度和深度分别为L和H，第一个空腔距离入口的长度为L_u，最后一个空腔距离出口的长度为L_d ，计算域的高度为D。S₁采用漫反射壁面边界条件，S₂、S₃采用速度入口边界，S₄采用出口边界条件。在本文的模拟中，L_u = L_d = 50, D = 30, L = H = W = 1。凹坑内部物理网格40×40，远场物理网格440×40。速度空间采用30×30的Gauss-Hermite积分点。当两个连续1000步在凹坑中心速度相对差小于1×10^–6时，流动达到稳态。

图  2  计算域示意图

Figure  2.  Schematic diagram of computation domain

下载: 全尺寸图片 幻灯片

表1展示了本文模拟中采用的计算参数表，其中分子平均自由程λ通过公式（8）求出：

表  1  计算参数表

Table  1.  Computation parameters

计算参数	计算值
U/(m·s-1)	68.1
T/K	288.15
ρ/(kg·m-3)	1.29
μ/(Pa·s)	1.79×10–5
λ/m	6.1×10–8

下载: 导出CSV 

| 显示表格

式中：ω为常数，取决于分子间相互作用模型，本文采用HS模型，ω = 0.5。

由于DUGKS具有渐进保持性质，时间步长与克努森数的粒子碰撞时间无关，因此可由CFL方法确定：

其中：α是CFL数，本次模拟中对于所有情况，α = 0.5，Δx是最小网格间距，ξ_m是最大离散速度，U_m是最大流体速度。

在本次模拟中凹坑采用方形结构，以凹坑深度H为特征长度，此时克努森数的物理含义为无量纲凹坑深度。后续结果中以克努森数表征凹坑尺寸。

3.   结果与讨论

在本文研究中，X和Y表示凹坑内的相对位置，速度通过该处的速度离散空间分布函数的统计平均求出，凹坑表面的滑移速度u定义为凹坑表面在与平滑壁面等高平面上的流向速度，平滑壁面处的滑移速度U_wall定义为在该处通过漫反射边界条件得到的流向速度。没有特别说明的情况下，速度以无穷远来流速度U_∞无量纲化，压力系数C_p的定义如下：

其中，来流动压q_∞ = ρ_∞U_∞²/2。

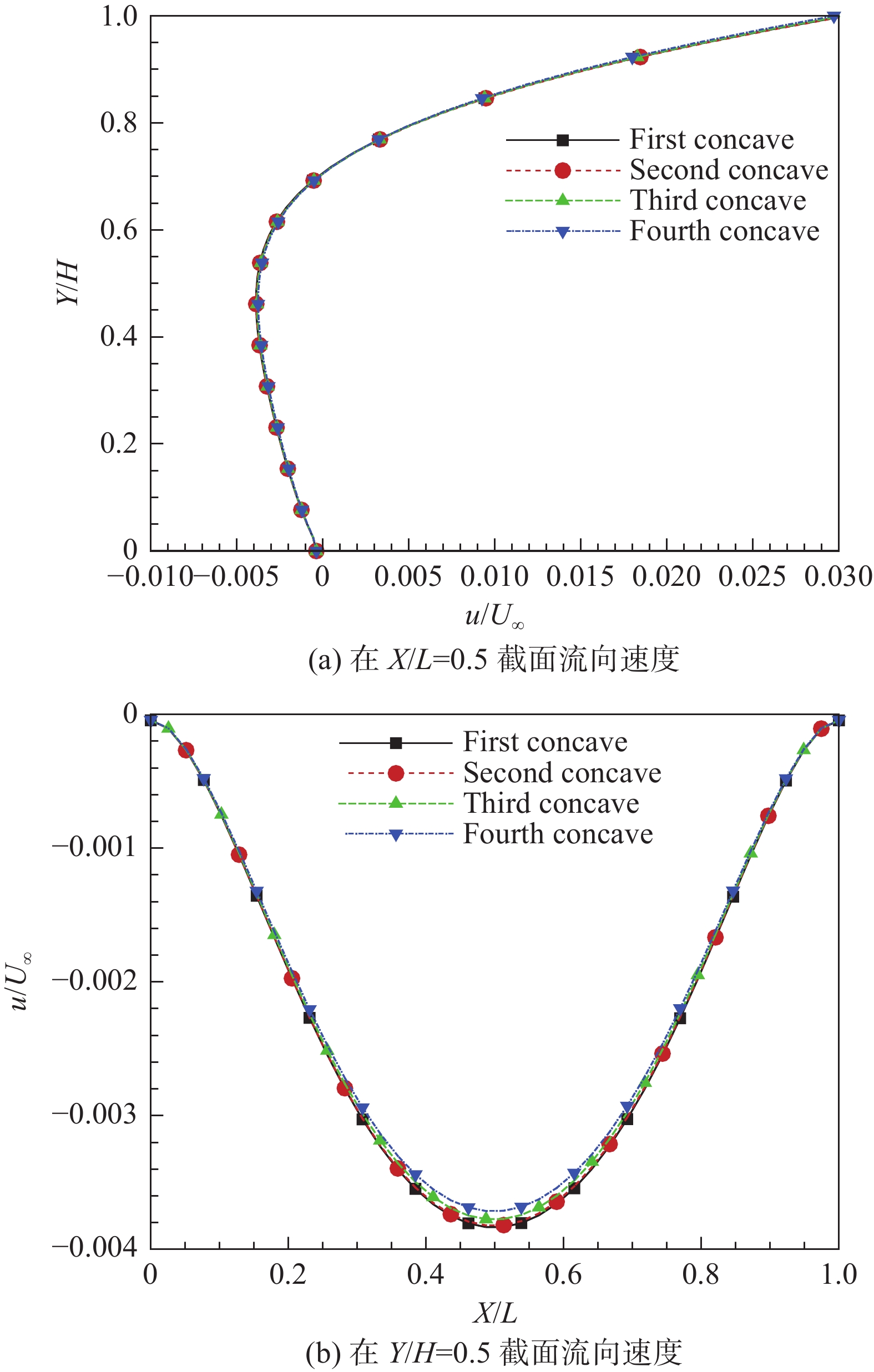
图3展示了在Kn为0.01时四个凹坑在X/L = 0.5与Y/H = 0.5处的流向速度曲线，结果表明第一个凹坑与其他三个凹坑的流动结果相差不大，且与后续分析中得出的规律相同。因此后续只给出第一个凹坑的流动结果。

图  3  四个凹坑内不同截面流向速度曲线

Figure  3.  Streamwise velocity profiles at different slice in four cavities

下载: 全尺寸图片 幻灯片

3.1   凹坑表面滑移特性分析

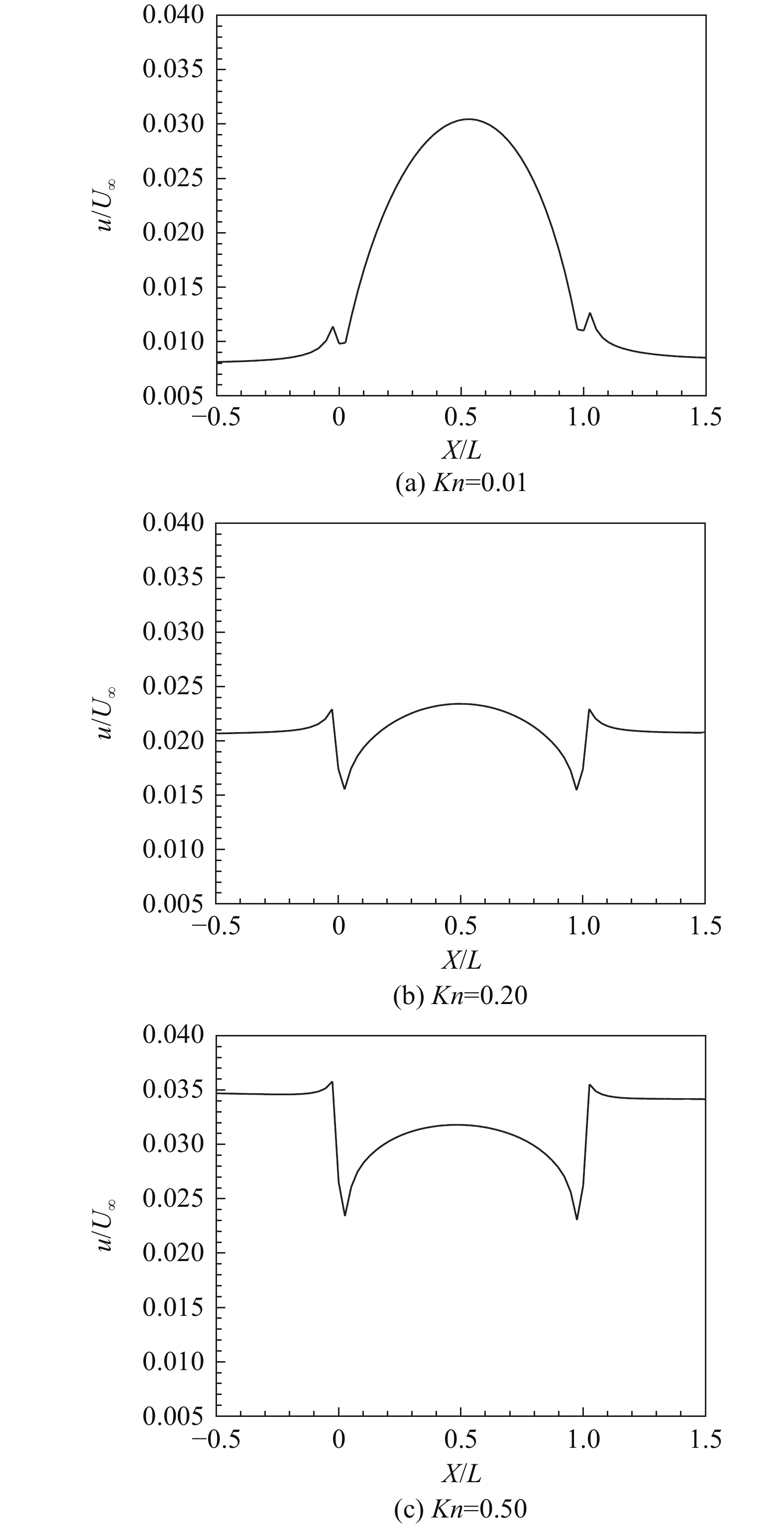
图4（a、b、c）分别展示Kn为0.01、0.2和0.5时在y = 0截面处凹坑表面及其附近壁面的滑移速度剖面。流动在流经拐角后，由于拐角处流动方向的改变，流动方向从沿着壁面的流向转变为向凹坑内部的法向，均出现滑移速度陡降的现象，随后沿着流向距离增加，流向速度慢慢增大，在空腔中线达到最大，并且速度关于空腔中心呈近似对称分布。从上述图中可以清楚看到，对应Kn为0.01、0.2和0.5时，分别呈现“上凸”和“下凹”型的滑移速度剖面。在不同的克努森数下（对应着不同的微结构尺寸），滑移速度剖面呈现明显的差异。

图  4  y = 0截面处滑移速度剖面

Figure  4.  Slip velocity profiles at y = 0

下载: 全尺寸图片 幻灯片

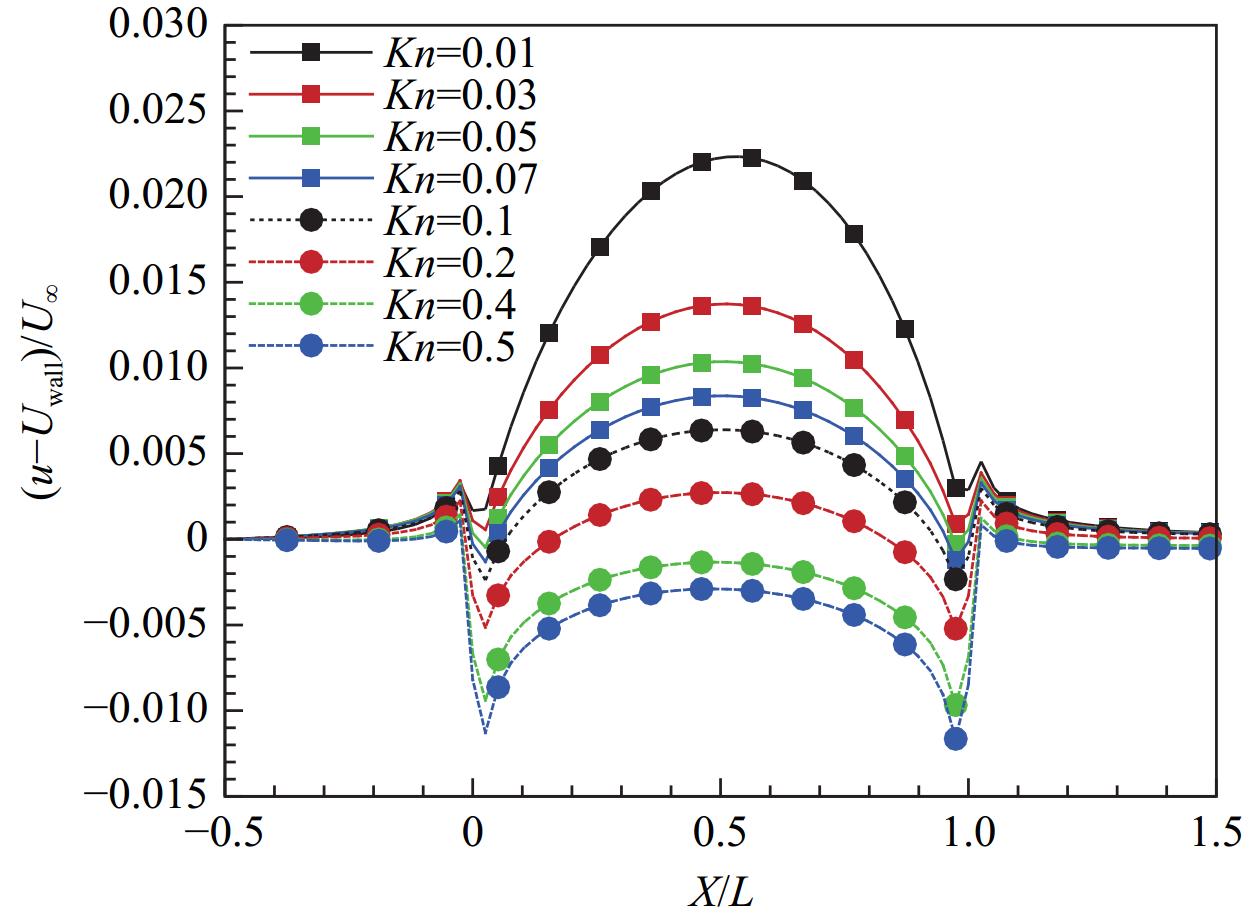
图5分别展示了在Kn = 0.01～0.5范围内，凹坑表面滑移速度与壁面滑移速度的速度差（u−U_wall）曲线。在Kn = 0.01～0.2范围内，凹坑表面的滑移速度均大于平滑壁面速度，速度差曲线呈现“上凸”型规律，且随着克努森数的增大，即凹坑尺寸的减小，曲线“上凸”的幅度增大。在Kn = 0.3～0.5范围内，凹坑表面的滑移速度均小于平滑壁面速度，速度差曲线呈现“下凹”型规律，且随着克努森数的减小，即凹坑尺寸的增大，曲线“下凹”的幅度增大。在Kn = 0.2时，凹坑表面的平均滑移速度近似等于平滑壁面处滑移速度，因此可认为Kn = 0.2是该模型的临界克努森数。

图  5  凹坑表面滑移速度与壁面滑移速度的速度差曲线

Figure  5.  The difference between slip velocities on the concave ans smooth walls

下载: 全尺寸图片 幻灯片

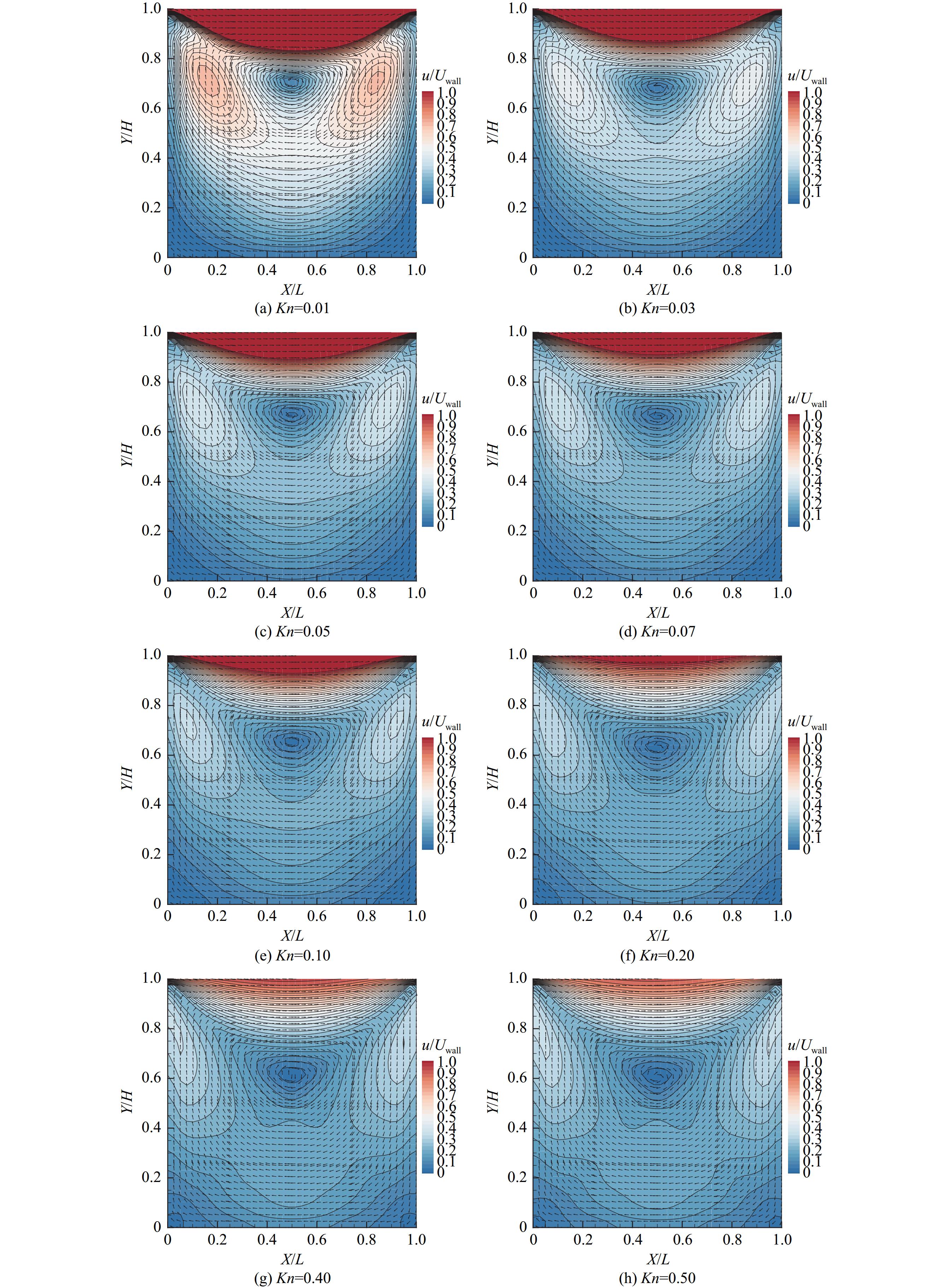
图6分别展示了Kn = 0.01～0.5的以壁面速度U_wall无量纲化的速度等值线云图。该图结果表明在Kn = 0.01～0.5范围内，随着克努森数增大，凹坑尺寸减小，凹坑内部分子碰撞频率降低，导致旋涡强度减小，凹坑内部剪切层的厚度增加。剪切层随着克努森数增大，越来越深入凹坑内部，压缩了凹坑内部的旋涡，涡心下移，在凹坑表面的分子相互碰撞进入凹坑后更不容易离开凹坑。

图  6  Kn = 0.01～0.5范围内速度等值线云图

Figure  6.  Velocity contours within the range of Kn = 0.01～0.5

下载: 全尺寸图片 幻灯片

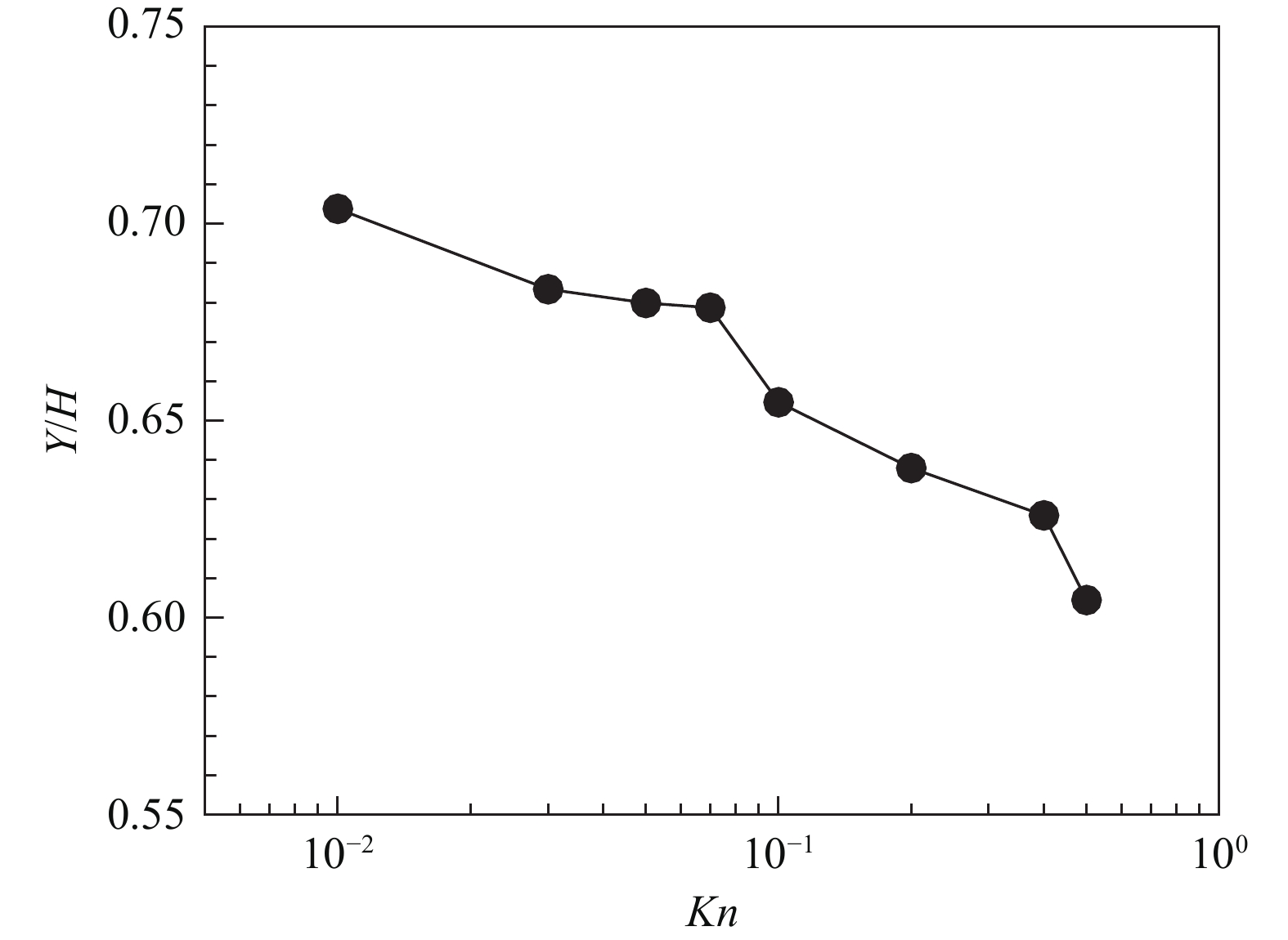
图7展示了旋涡中心法向距离随Kn变化，随着克努森数的增加，旋涡中心向凹坑底部移动。涡心的下移影响凹坑内部的速度分布，导致图7所示的凹坑表面附近的区域速度越来越低。在Kn = 0.01～0.2范围内，凹坑表面附近分子携带的动量相对于平滑壁面分子携带的动量较高，与凹坑外部的气体分子相碰撞，导致凹坑区的滑移速度大于平滑壁面的滑移速度。在Kn = 0.3～0.5范围内，凹坑表面附近分子携带的动量相对于平滑壁面分子携带的动量较小，与凹坑外部的气体分子相碰撞，导致凹坑区的滑移速度小于平滑壁面的滑移速度。

图  7  旋涡中心法向距离随Kn的变化

Figure  7.  Variation of the wall-normal distance of the vortex center with Kn

下载: 全尺寸图片 幻灯片

3.2   凹坑表面滑移速度跳跃现象分析

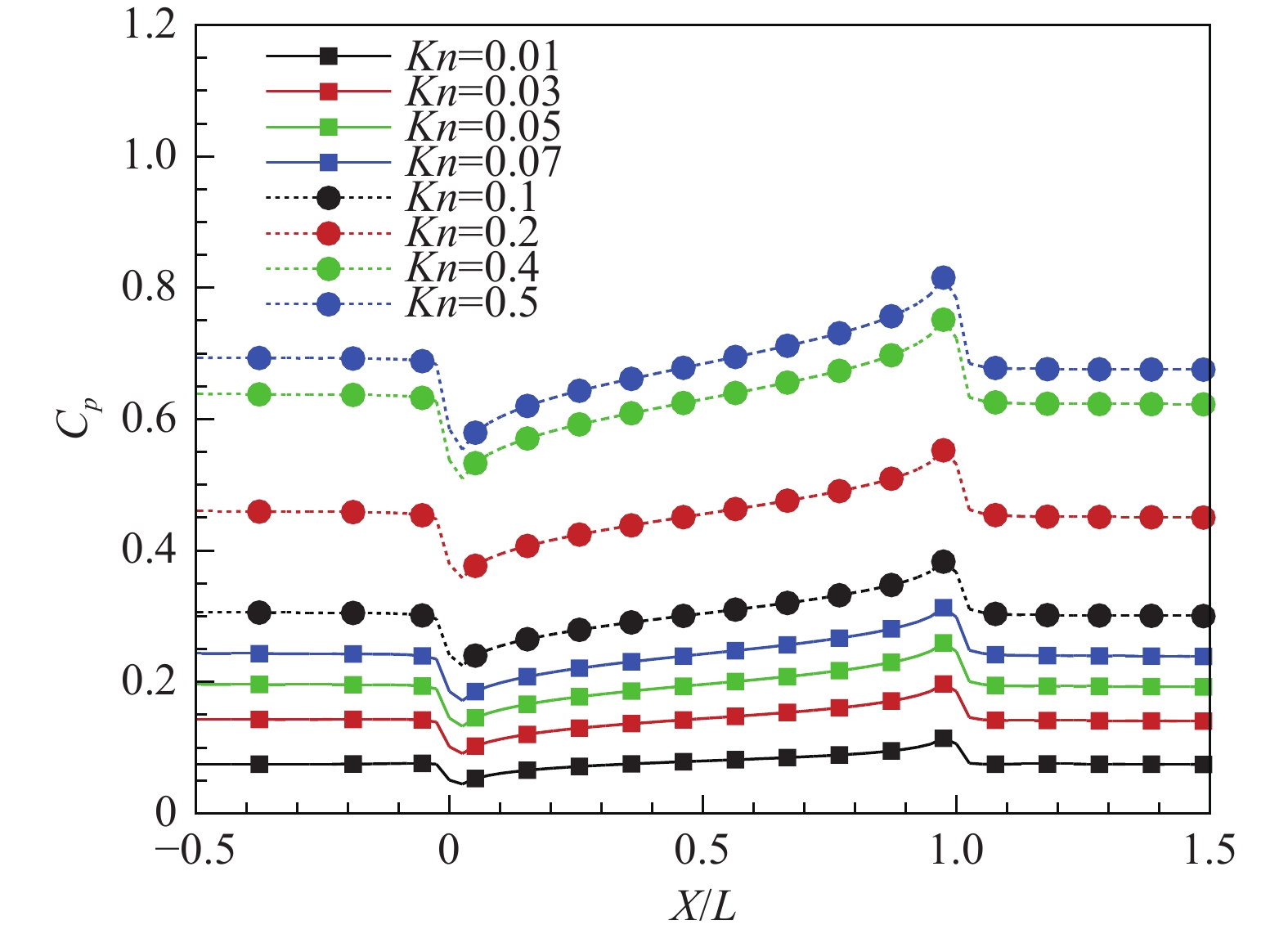
图5中，在凹坑拐角两侧出现了滑移速度跳跃现象，即拐角前后出现了明显的滑移速度差，且随着克努森数的增加，滑移速度跳跃的幅度增加。图8展示了在y = 0截面处凹坑表面及其附近壁面的压力系数曲线。随着克努森数的增加，凹坑上游处的压力系数降低。压力系数在经过拐角后先降低，然后随着流向距离增加而上升。

从宏观状态分析，在凹坑两侧几何形状的极速变化，导致了流体的膨胀和压缩，使凹坑两侧拐角处出现低压区和高压区。经过拐角后，由于没有壁面边界条件阻碍流体向法向流动，流向速度减小，法向速度增大。从微观角度分析，分子在经过拐角之前，与壁面碰撞发生漫反射，壁面阻碍了分子向法向流动，由于拐角处的低压区，使分子只能沿流向加速向拐角流动，因此在拐角之前流向速度增加。在到达拐角时，分子与分子碰撞，产生法向速度，此时分子流入凹坑，使流向速度转换为法向速度。这解释了滑移速度剖面在拐角处的陡降现象。随着克努森数的增加，拐角附近的压强差越大，因此导致了更大幅度的滑移速度跳跃。

图  8  y = 0截面处压力系数曲线

Figure  8.  Pressure coefficient distributions at y = 0

下载: 全尺寸图片 幻灯片

3.3   凹坑表面滑移速度模型

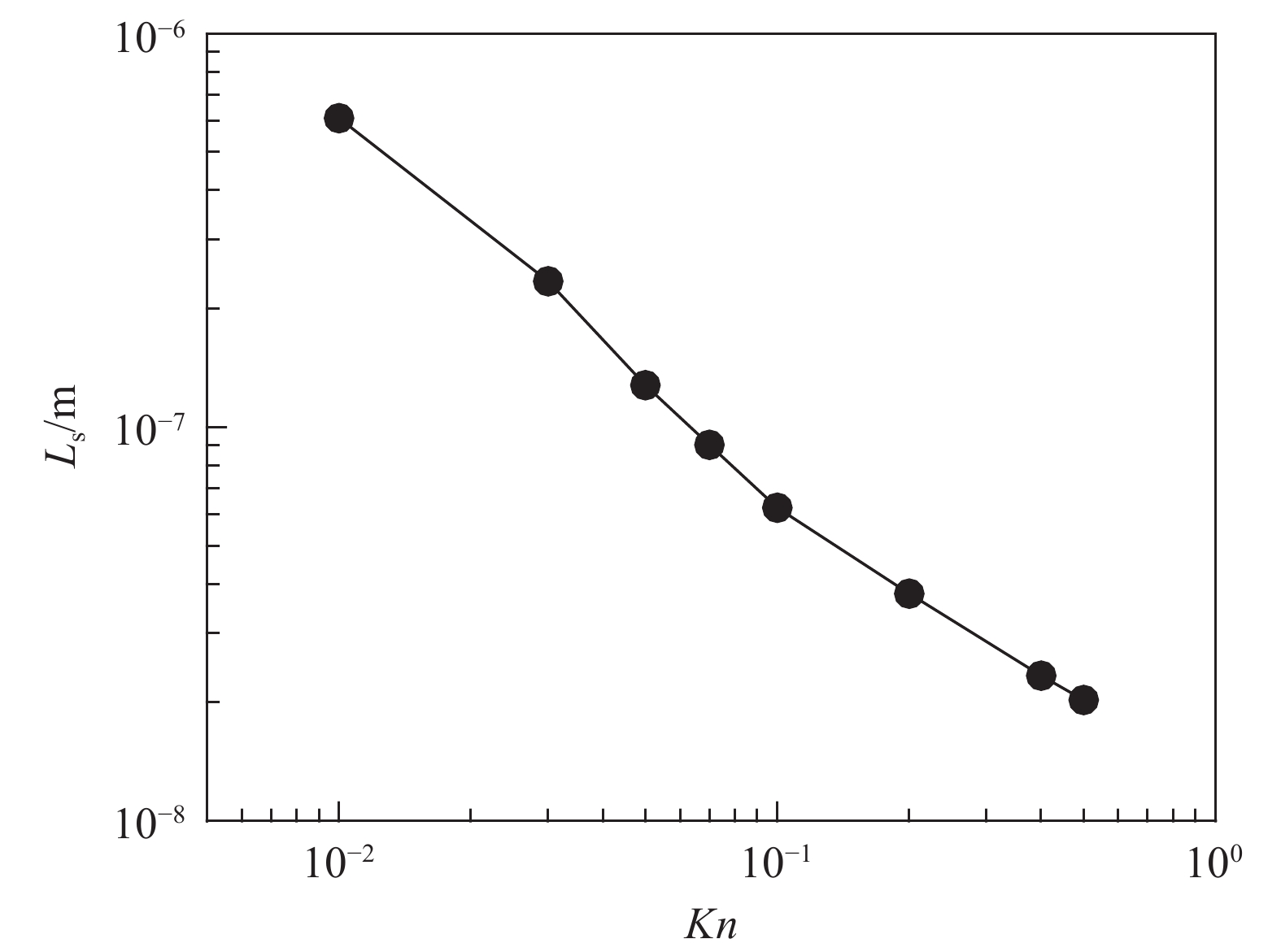
表2和图9展示了克努森数与滑移长度的关系。总体趋势是随着克努森数的减小，凹坑尺寸增大，滑移长度越大，且lgL_s与lgKn的关系基本满足关系式：lgL_s = algKn+b。对于本次凹坑构型的研究，a = −0.6712，b = −5.2864。虽然实际上克努森数越大滑移长度越长，但从凹坑表面滑移特性方面来说，应在设计疏水微结构时，Kn不能大于0.3。

表  2  Kn与滑移长度关系

Table  2.  Relationship between Kn and slip length

Kn	特征长度/m	滑移长度/m
0.01	6.10×10–6	6.10×10–7
0.03	2.03×10–6	2.35×10–7
0.05	1.22×10–6	1.28×10–7
0.07	8.71×10–7	9.03×10–8
0.1	6.10×10–7	6.25×10–8
0.2	3.05×10–7	3.78×10–8
0.4	1.52×10–7	2.34×10–8
0.5	1.22×10–7	2.03×10–8

下载: 导出CSV 

| 显示表格

图  9  滑移长度随Kn变化曲线

Figure  9.  Variation of slip length with Kn

下载: 全尺寸图片 幻灯片

4.   结　论

本文通过DUGKS方法对Kn = 0.01～0.5范围内疏水材料中的方形凹坑结构进行数值模拟，对比分析了不同克努森数对凹坑表面的滑移速度特性的影响。得到的主要结论如下：

1） 不同的克努森数下，凹坑表面的滑移速度特性出现明显差异。在Kn = 0.01～0.2范围内，随着克努森数减小，凹坑尺寸增大，凹坑内部旋涡强度增大，流向速度大于平滑壁面的流向速度。在Kn = 0.3～0.5范围内随着克努森数增大，凹坑尺寸减小，凹坑内部分子减少，分子间碰撞频率降低，剪切层更加深入凹坑内部，凹坑区的滑移速度小于平滑壁面的滑移速度。

2） 滑移速度在经过凹坑拐角处均会出现滑移速度跳跃现象，且滑移速度跳跃的幅度随着克努森数增加而增强。

根据本文计算结果，不同克努森数（对应不同微结构尺寸）下的凹坑流的滑移特性存在明显差异，且均存在滑移速度跳跃现象。从凹坑表面滑移特性来说，在设计疏水微结构时，Kn不能大于0.3。

本文只考虑了疏水材料的凹坑型疏水结构，但实际的疏水结构中凹坑型只占一小部分，还有更多疏水结构的滑移特性需要探索，并且不同的疏水结构表现出的滑移效果必然有所差异。同时，本文尚未考虑疏水结构的三维效应，疏水结构在三维上进行排列组合后是否能得到更好的滑移特性，这也是下一步的研究方向。