0.   引　言

翼尖涡是有限翼展机翼上下表面因存在压力差而产生的大尺度涡结构。飞机翼尖涡会带来诱导阻力，并引发尾迹遭遇等问题。后机遭遇前机尾流时，可能引发机身倾斜、滚转、失速或急剧俯仰，严重影响飞行安全。为此，国际民航组织（ICAO）制定了严格的尾流间隔标准，根据不同的前后机重量分类，在同一机场跑道上设定了4～8海里不等的尾流间隔距离或2～3分钟的起降间隔时间，而这也成为限制机场起降频率和运行效率的主要因素之一^[1]。厘清翼尖涡在不同来流条件下的演化耗散特性，对实际飞行条件中尾涡的实时监测/预测及开发相应的流动控制技术具有重要的实际意义。

来流湍流度是影响翼尖涡衰减耗散行为的重要因素。Sarpkaya等^[2]、Bandopadhya等^[3]以及Liu^[4]通过流动显示实验观察到高来流湍流度能够缩短翼尖涡的生命周期，从而加速其破碎。Ahmadi等^[5]、Bailey等^[6]以及Heyes等^[7]通过实验测量发现湍流度的增大对翼尖涡切向速度衰减起到加速作用。近年来，Ghimire等^[8]通过进行粒子图像测速（particle image velocimetry, PIV）实验，详细研究了孤立翼尖涡在不同来流湍流度下的发展与衰减行为，并尝试通过涡剥离（vortex stripping）现象解释翼尖涡的耗散。Dghim等^[9]研究了不同来流湍流度下的翼尖涡沿程发展及速度脉动特性，并分析了翼尖涡内部拟涡能的输运机制。

另一方面，翼尖涡会表现出不稳定的摇摆运动，翼尖涡的摇摆运动同样对来流湍流度较为敏感。薛栋等^[10-11]通过流动显示方法定量测量了摇摆运动的不稳定频率，在此基础上分析了翼尖涡的统计特性。Bailey等^[6]通过热线测速仪测量发现翼尖涡摇摆运动幅值随来流湍流度增强而显著增大，但其波长对来流湍流度并不敏感。Van Jaarsveld等^[12]进一步发现，翼尖涡摇摆运动幅值与湍流度和翼尖涡翻转时间（turnover time）的平方根呈线性关系。而后Bailey等^[13]分析了摇摆运动的幅值频率特点以及标度特性，并将摇摆运动受来流湍流的影响机理归结于翼尖涡与湍流场中小尺度涡结构^[14]的相互作用。现有研究的实验条件与相关参数总结见表1，虽然针对来流湍流度对孤立翼尖涡的影响已有一定研究，但在高湍流度下翼尖涡中远场高时空分辨率速度测量方面仍比较欠缺，对高湍流度下翼尖涡中远场的衰减行为、不同湍流度下翼尖涡摇摆运动演化与机理等方面尚未认识清楚。

表  1  相关研究及对应实验参数

Table  1.  relevant research and the corresponding experimental setups

相关研究	实验方法	雷诺数/104	湍流度/%	测量范围x/c
Heyes等[7]（2004）	风洞二维PIV实验	10, 22	1, 2.2, 3.2	1～22.9
Jaarsveld等[12]（2011）	风洞二维PIV实验	8	< 0.5, 2.1	3.5～37.6
Bailey等[6, 13]（2008、2018）	风洞热线风速仪实验	24	0.4, 2.5, 5	3.75～9.75
Ghimire & Bailey [8, 15]（2017、2018）	水槽SPIV实验	1.2	0.4, 2.5, 6.8	0～10
Dghim等[9]（2020）	水洞SPIV实验	20	0.5, 3, 6	1.25～7.75

下载: 导出CSV 

| 显示表格

基于以上背景，本文针对不同来流湍流度下，中远场范围内的孤立翼尖涡演化规律开展实验研究，旨在为建立不同湍流度下翼尖涡衰减预测方法及开发相应的流动控制技术提供依据。为此，本研究通过时间解析的体视粒子图像测速技术（time resolved-stereo particle image velocimetry, TR-SPIV）获取了自由来流及格栅湍流条件下孤立翼尖涡的速度场，并对不同来流条件下翼尖涡的摇摆运动及统计特性演化规律进行分析，以探究来流湍流度对翼尖涡不稳定运动与衰减演化特性的影响。

1.   实验搭建与数据处理

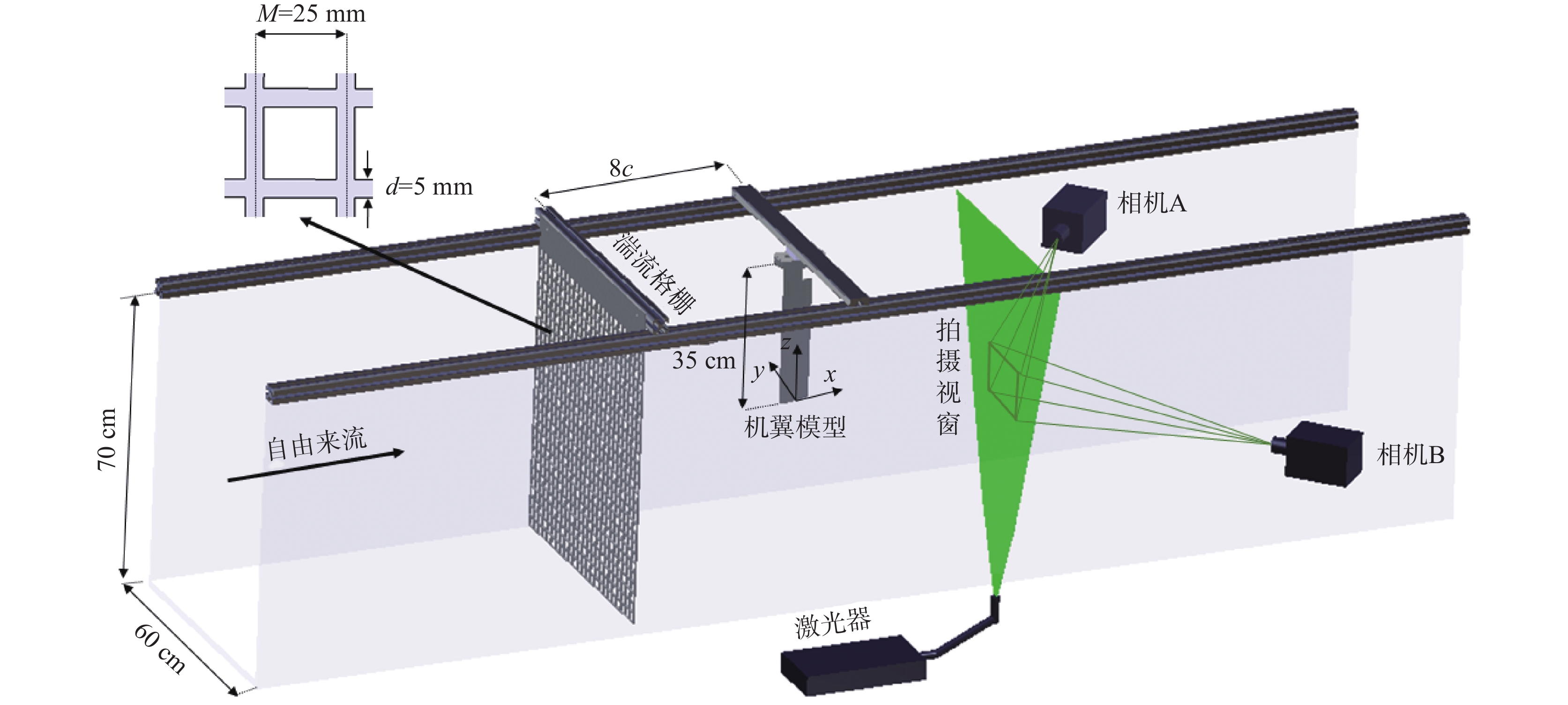
实验在北京航空航天大学的低速回流式水槽中完成，水槽实验段的尺寸为3 m × 0.6 m × 0.7 m（长 × 宽 × 高）。实验布置如图1所示，为简化研究对象，实验采用翼尖涡研究中常用的NACA0012翼型等直机翼模型。机翼采用ABS树脂一次性机加工成型，尾缘厚度小于0.1 mm。机翼弦长c = 8 cm，展长b = 35 cm，对应展弦比AR = 4.375。实验中机翼迎角α = 6°，翼尖距水槽水面距离约35 cm，相对于翼尖涡的尺寸足够远，水面处的波动界面不会对翼尖涡的摇摆运动产生显著影响。通过布置在机翼模型上游的湍流格栅产生来流湍流，湍流格栅的设计与布置参考格栅湍流特性相关研究^{[8, 16-17]}，采用方形网格、方柱栅条，网格尺寸M = 25 mm，栅条宽度h = 5 mm，格栅孔隙比σ = 0.36。格栅安装于机翼模型上游8c（128h）的位置，即x_grid = −8c，以保证按照来流条件要求在机翼及其下游产生近似各向同性均匀湍流。文中的笛卡尔坐标系原点位于机翼梢部二分之一弦长处，x、y、z坐标轴方向分别与来流方向、机翼升力方向和展向方向平行。考虑到本文的研究目的是研究来流湍流度对翼尖涡动力学特性和沿程变化规律的影响，实验时保持自由来流速度U_∞ = 124 mm/s不变，实验水温恒定为25 ℃，对应的运动黏性系数ν = 0.8731 × 10⁻⁶ m²/s，基于机翼弦长的雷诺数$R{e_c} = {{{U_\infty }c} \mathord{\left/ {\vphantom {{{U_\infty }c} \nu }} \right. } \nu } \approx 1.1 \times {10^4}$。本文实验设置与Hrynuk等^[18]的实验类似，其流场结果可作为实验模型流动情况的参考。

图  1  实验布置示意图

Figure  1.  Schematic of the experimental setup

下载: 全尺寸图片 幻灯片

实验采用TR-SPIV获取流场三分量速度场信息。示踪粒子采用直径为5～10 μm的空心玻璃珠，密度为1.05 g/cm³。采用Nd-YAG （Vlite-500）高频双曝光激光器输出激光，激光输出能量为50 mJ/pulse, 经透镜组整形后形成厚度约为2 mm的片光，并由水槽底部光学玻璃垂直入射照亮测量平面。通过平移滑轨改变机翼到激光平面的距离，在x/c = 2～16范围内等间距测量了8个流向站位的翼尖涡尾流场。粒子图像通过两台高速CMOS相机（Photron FASTCAM SA2/86 KM3）搭配180 mm微距镜头（TAMRON SP AF 180 mm F/3.5 MACRO 1∶1）采集，相机分辨率为2048 pixels × 2048 pixels。拍摄视窗大小为85 mm（y向） × 65 mm（z向），对应的空间分辨率约为24 pixels/mm。两相机对称布置于水槽两侧，相机透视角为45°，在相机与水洞壁面之间安装水棱镜以减小不同介质之间折射的影响。通过同步器（SM-MicroPulse725）实现激光器与相机之间的同步控制。拍摄时的采样频率为f = 100 Hz，每组连续测量记录2725对粒子图像，在每个流向站位处连续采集3组粒子图像，以保证二阶湍流统计量收敛。

获得粒子图像后，采用课题组自编的多层迭代Lucas-Kanade（multi-pass iterative Lucas-Kanade, MILK）光流算法^[19]计算速度场，通过空间标定将两台相机像平面上的二维二分量速度场映射至测量平面获得二维三分量速度场。计算的最终查询窗口尺寸为32 pixels × 32 pixels，重叠率为75%。速度场的最终测量误差不超过1%，满足后续分析要求。

2.   实验结果及分析

2.1   格栅湍流场标定

在不安装机翼模型的情况下，首先通过SPIV实验获取湍流格栅后的速度场，对格栅湍流的性质进行标定。分析湍流统计量时，将流场中的瞬时速度u分解为平均量$\bar {\boldsymbol{u}}$和脉动量${\boldsymbol{u}}'$:

湍动能k通过式（2）定义：

湍流度$Tu$通过式（3）定义：

其中：${{\boldsymbol{u}}'_{{\mathrm{rms}}}} = \sqrt {\dfrac{1}{3}(\overline {{{u'}^2}} + \overline {{{v'}^2}} + \overline {{{w'}^2}} )} = \sqrt {\dfrac{2}{3}k}$，为脉动速度均方根值；u'、v'、w'分别为x、y、z方向的速度脉动。

湍流积分长度尺度$L$通过式（4）定义：

其中，$R(x)$为脉动速度空间自相关函数。

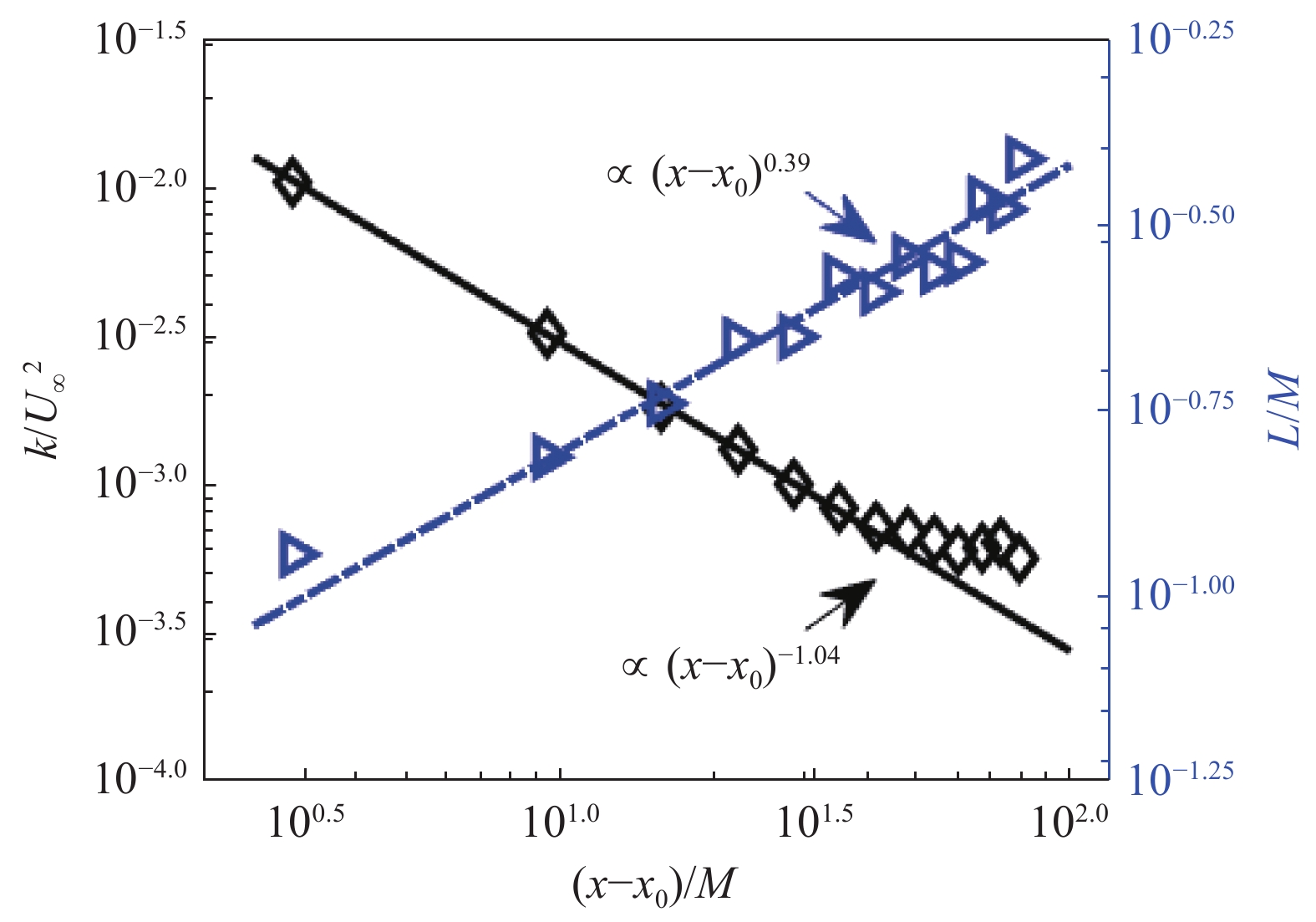
在不加装格栅的自由来流条件下，由式（3）和式（4）得到的来流湍流度与湍流积分长度分别为Tu = 0.83%与L = 2.25 mm。加装湍流格栅后，测量原点处Tu = 2.94%，L = 5.50 mm。沿流向分别对13个流向站位$(x - {x_{{\mathrm{grid}}}})/c = 2 {\text{～}} 26、\Delta {x \mathord{\left/ {\vphantom {x c}} \right.} c} = 2$的水槽中心区域进行拍摄获得速度场结果。在翼尖涡测量范围（x/c = 2～16）内，来流湍流度Tu由2.58%衰减到2.04%，湍流积分长度$L$由5.56 mm增长到8.25 mm。对于各向同性格栅湍流，k和L在向下游发展过程中理论上分别满足如下的幂律规律^[16-17]：

其中，$A$为拟合常数，x表示流向位置，x₀表示虚拟原点（virtual origin），M为格栅的网格尺寸。通常α值在1～1.5的区间内，β值为0.4。根据式（2）和式（4）计算不同流向位置处的湍动能和湍流积分长度尺度的变化，结果如图2所示。可以看到，本实验中产生的格栅湍流的湍动能和湍流积分长度尺度均能较好满足式（5）和式（6）的幂律规律。实验中得到的α = 1.04、β = 0.39，符合理论预期。注意到在下游位置，当x/M > 60时，湍动能数据点开始在一定程度上偏离幂律衰减规律，这一点在Ghimire等^[15]的结果中也有体现。

图  2  格栅湍流湍动能与湍流积分长度尺度沿流向发展情况

Figure  2.  Streamwise development of the turbulent kinetic energy and integral length scale for grid turbulence

下载: 全尺寸图片 幻灯片

2.2   翼尖涡流场测量结果

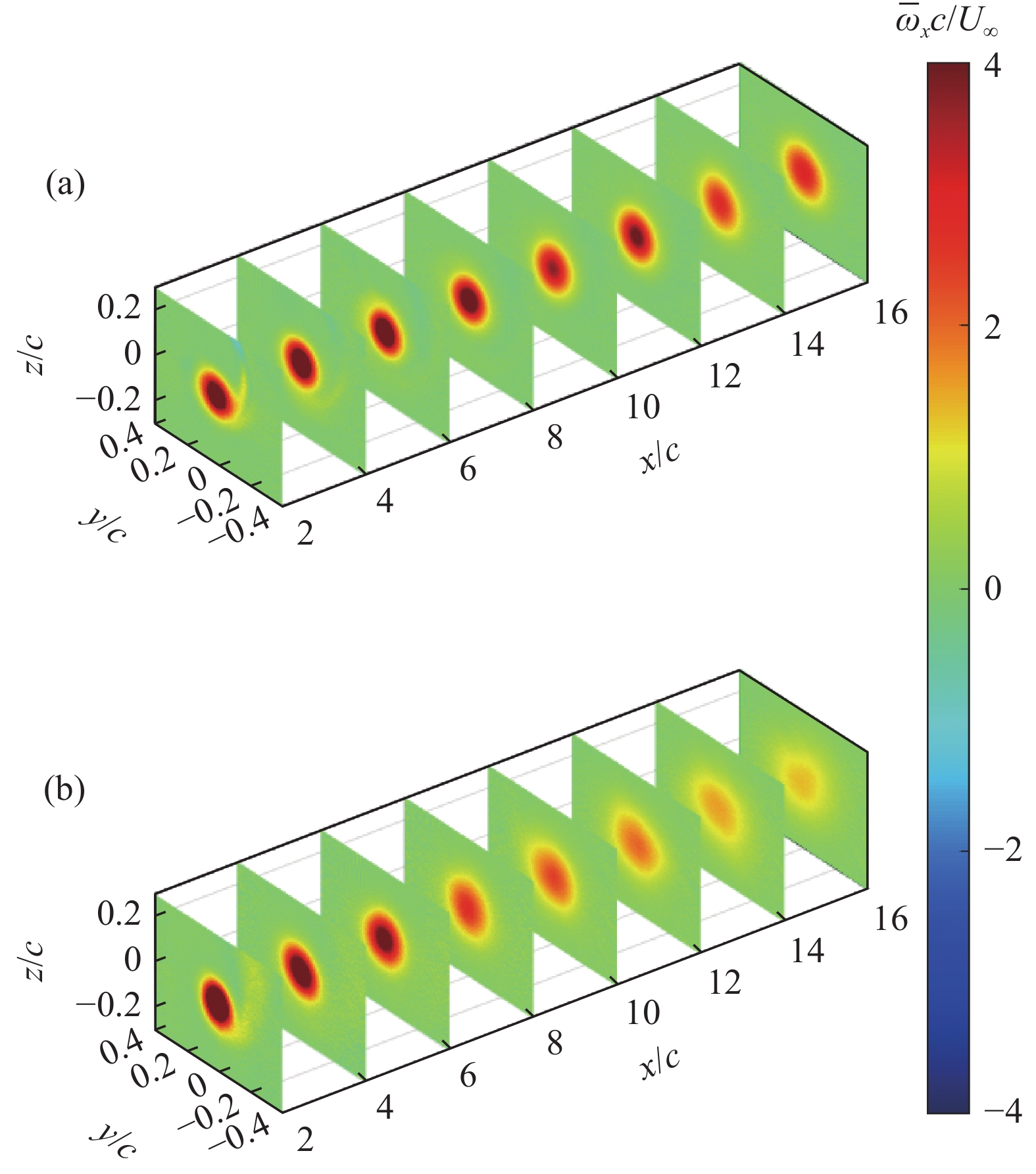
为直观说明来流湍流度对翼尖涡演化的影响，首先给出不同来流条件下所有测量平面内的时间平均流向涡量场沿程发展，其结果如图3所示。为便于对比，这里将平均涡心位置统一对齐至坐标原点。可以发现，在x/c = 2～4的近场区域，翼尖涡表现出较强且较为集中的流向涡量，同时流场中还能够观察到翼尖涡卷起过程中所形成的尾迹区域。在翼尖涡向下游发展的过程中，涡量分布逐渐发散。对比有无湍流格栅下的翼尖涡沿程发展情况可以看到，在格栅湍流作用下，翼尖涡时均流向涡量分布的分散程度显著增强。这主要是因为高湍流度下翼尖涡的不稳定摇摆运动显著增强，对时均流场的“抹平”效应增强。

图  3  翼尖涡时间平均流向涡量分布的沿程发展：（a）自由来流，（b）格栅湍流

Figure  3.  Time averaged axial vorticity contours along the streamwise positions: (a) free stream, (b) grid turbulence

下载: 全尺寸图片 幻灯片

2.2.1   翼尖涡摇摆运动及其对流场统计量的影响

翼尖涡的摇摆运动是指翼尖涡在其三维空间内的一种非定常、不稳定的运动，通常以翼尖涡涡心位置的运动来表征。翼尖涡瞬时涡心位置有多种不同的确定准则，包括涡量峰值、涡量质心公式、平面内速度极小值等^{[7, 20-21]}，比较后发现涡量质心公式方法在近场区域由于受机翼尾缘脱落尾迹影响而偏离实际的涡心位置，涡量峰值方法对网格分辨率和测量噪声敏感性较强。因此，综合考虑这三种方法识别涡心时的精准度与鲁棒性，本文选择监测瞬时流场翼尖涡区域平面内的速度极小值点来确定瞬时涡心位置。

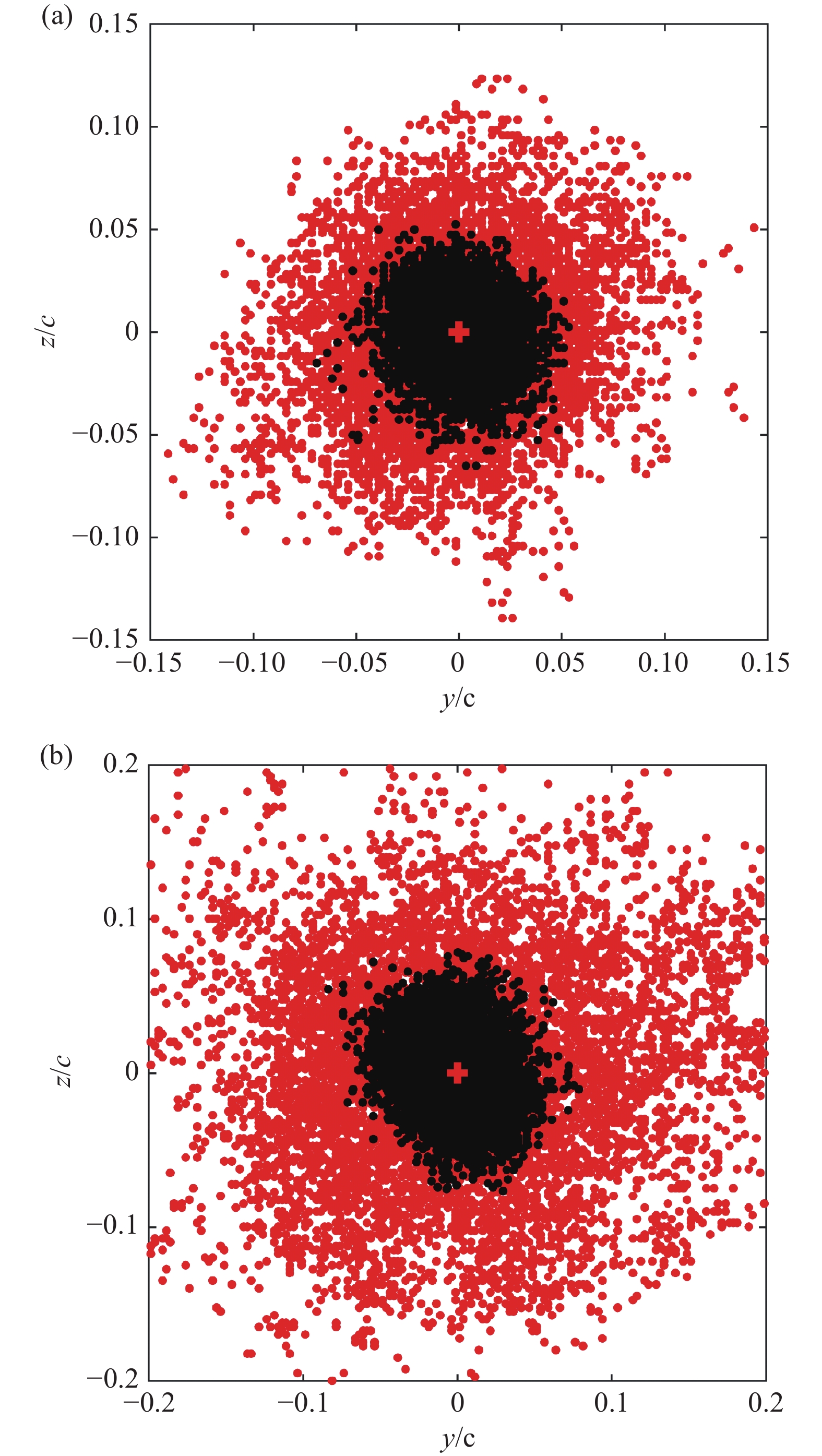
图4展示了x/c = 4与x/c = 10流向站位处不同来流条件下的瞬时涡心位置分布。可以发现，本实验中两种不同来流条件下孤立翼尖涡的涡心位置分布具有近似各向同性的特点；翼尖涡摇摆运动的强弱一般通过摇摆运动幅值$\sigma$进行表征，$\sigma = \sqrt {\sigma _y^2 + \sigma _z^2}$，其中${\sigma _y}、{\sigma _z}$分别为对应y、z方向上翼尖涡涡心位置的标准差。可以看到，随着湍流度的增大和向下游的发展，翼尖涡的瞬时涡心位置散布更加明显。具体而言，x/c = 4处，自由来流和格栅湍流条件下的摇摆运动幅值分别为1.22 mm和4.37 mm；而x/c = 10处，该数值分别为2.72 mm和8.38 mm，表明其摇摆运动明显增强。

图  4  翼尖涡瞬时涡心位置分布：(a) x/c = 4，(b) x/c = 10（黑色散点对应自由来流条件，红色散点对应格栅湍流条件）

Figure  4.  Distribution of the instantaneous vortex center: (a) x/c = 4, (b) x/c = 10. Herein, black scatters are for free stream, red scatters are for grid turbulence

下载: 全尺寸图片 幻灯片

翼尖涡的不稳定摇摆运动会显著影响翼尖涡的速度、涡量以及涡核半径等统计量的测量结果，给实验分析带来了明显的复杂性和干扰。在实验分析中需要通过修正算法消除翼尖涡摇摆运动的影响。本文采用基于PIV数据的系综平均流场修正方法^{[7, 22]}，也被称为涡心重新对齐（re-center）方法。系综平均要求计算流场统计量时首先将瞬时流场涡心对齐至平均涡心位置，然后再进行平均，从而得到流场结果。与之相对的平均方式为时间平均，操作上直接对瞬时流场数据求平均即可。

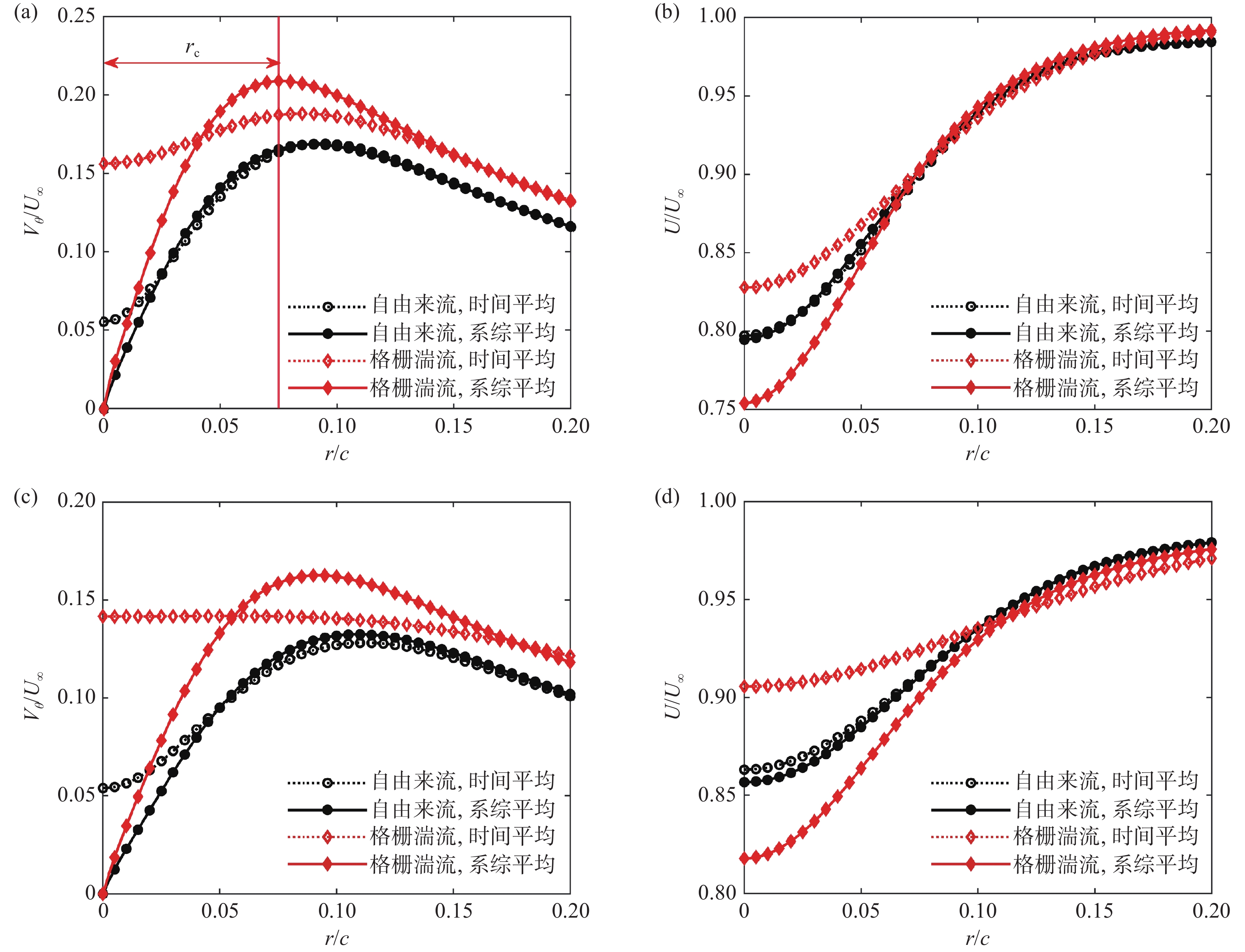
图5给出了流向站位x/c = 4与x/c = 10处自由来流及格栅湍流条件下时间平均与系综平均得到的周向平均速度剖面对比。可以看到在自由来流条件下系综平均与时间平均流场结果相差较小；而格栅湍流条件下翼尖涡摇摆运动更加剧烈，对翼尖涡附近的平均速度场产生明显的“抹平”效应。具体而言，在x/c = 4的流向站位处，时间平均结果中切向速度峰值被低估，同时涡核半径r_c（定义为切向速度剖面峰值对应的径向距离）被高估。对流向速度剖面而言，翼尖涡区域有流向速度亏损，涡核处的速度亏损在时间平均结果中被低估。而在x/c = 10的站位处，格栅湍流条件下翼尖涡摇摆运动幅值大，抹平效应更强，从时间平均速度剖面中已无法获取涡核半径等信息。

图  5  时间平均与系综平均修正后周向平均速度剖面的对比：(a～b) x/c = 4处切向速度及流向速度剖面，(c～d) x/c = 10处切向速度及流向速度剖面

Figure  5.  Comparison of velocity profiles by time averaging and ensemble averaging: (a-b) tangential and streamwise velocity profiles at x/c = 4, (c-d) tangential and streamwise velocity profiles at x/c = 10

下载: 全尺寸图片 幻灯片

此外，从图5中还可以发现，本实验中格栅湍流条件下的翼尖涡测量结果相比自由来流条件具有更大的切向速度峰值与流向速度亏损，表现出更强的环量，意味着翼尖涡的强度更强。这是因为低雷诺数自由来流条件下机翼模型表面存在分离泡，使得机翼升力系数下降，而在高湍流度条件下，机翼表面分离泡被抑制，升力系数更大，从而表现出更高的翼尖涡强度。这与Hrynuk等^[18]研究不同湍流度下机翼升力曲线特性及流动特征的结果相吻合。

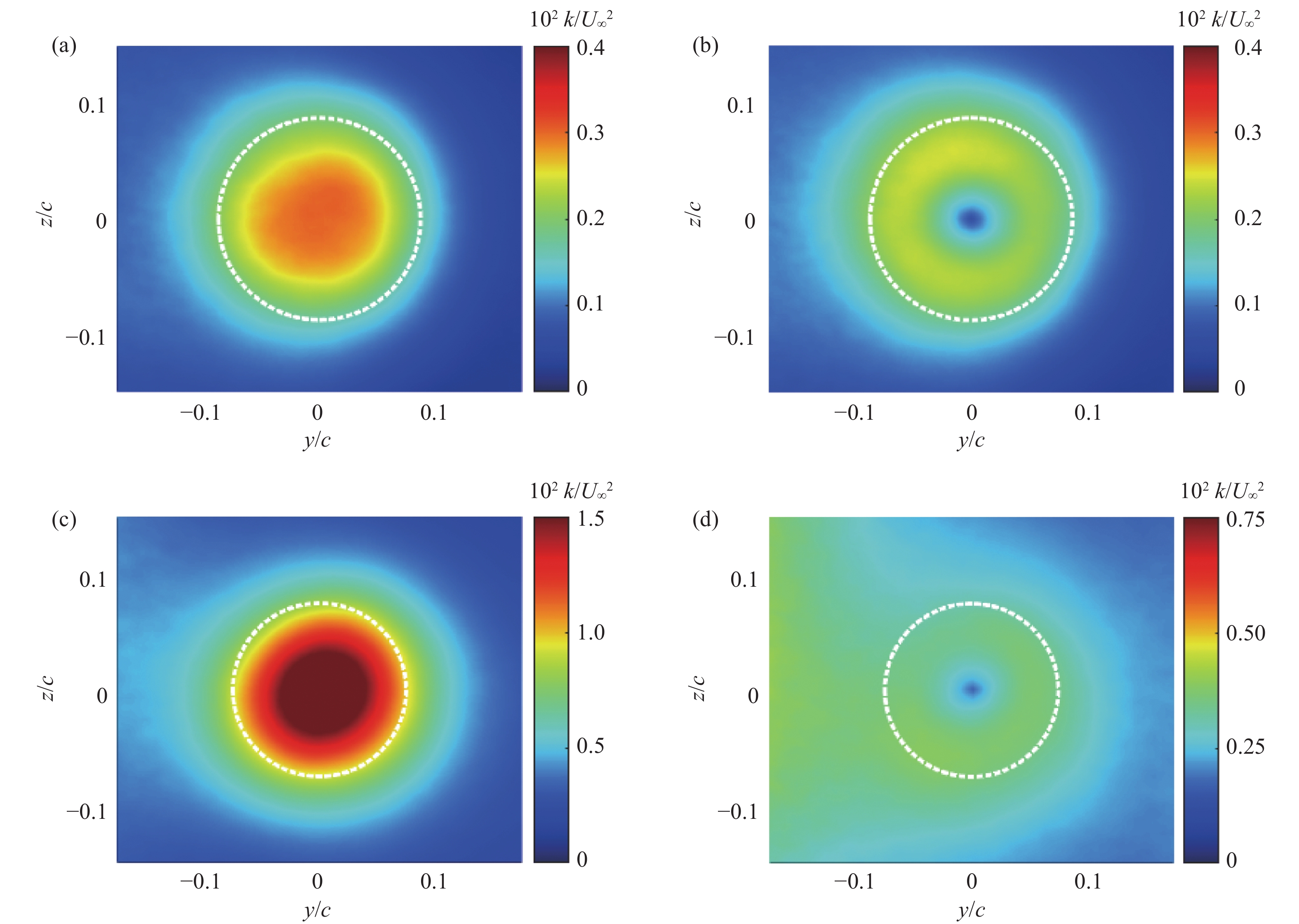
翼尖涡流场速度脉动特性及湍流统计量的测量同样会受到摇摆运动的显著影响，图6展示了x/c = 4的流向站位处不同来流条件下时间平均与系综平均修正后的湍动能分布，其中虚线内为涡核半径所包围的区域。对比修正前后的湍动能分布，可以看到修正后的湍动能显著低于修正前的结果，说明修正前流场的速度脉动主要来自摇摆运动的贡献，而通过系综平均方法能有效消除摇摆运动对速度脉动测量结果的影响。同时注意到修正后翼尖涡涡心附近湍动能强度明显降低^{[9, 23]}。这也与前人的理论分析相一致，即在黏性涡核旋转作用下，翼尖涡内部的湍流脉动受到强烈抑制^[24-25]。

图  6  x/c = 4处系综平均修正前后的湍动能分布：(a～b) 自由来流下时间平均与系综平均结果，(c～d) 格栅湍流下时间平均与系综平均结果

Figure  6.  Turbulent kinetic energy contours before and after ensemble averaging at x/c = 4: (a-b) time averaged and ensemble averaged results for freestream condition, (c-d) time averaged and ensemble averaged results for grid turbulence condition

下载: 全尺寸图片 幻灯片

2.2.2   翼尖涡摇摆运动演化规律

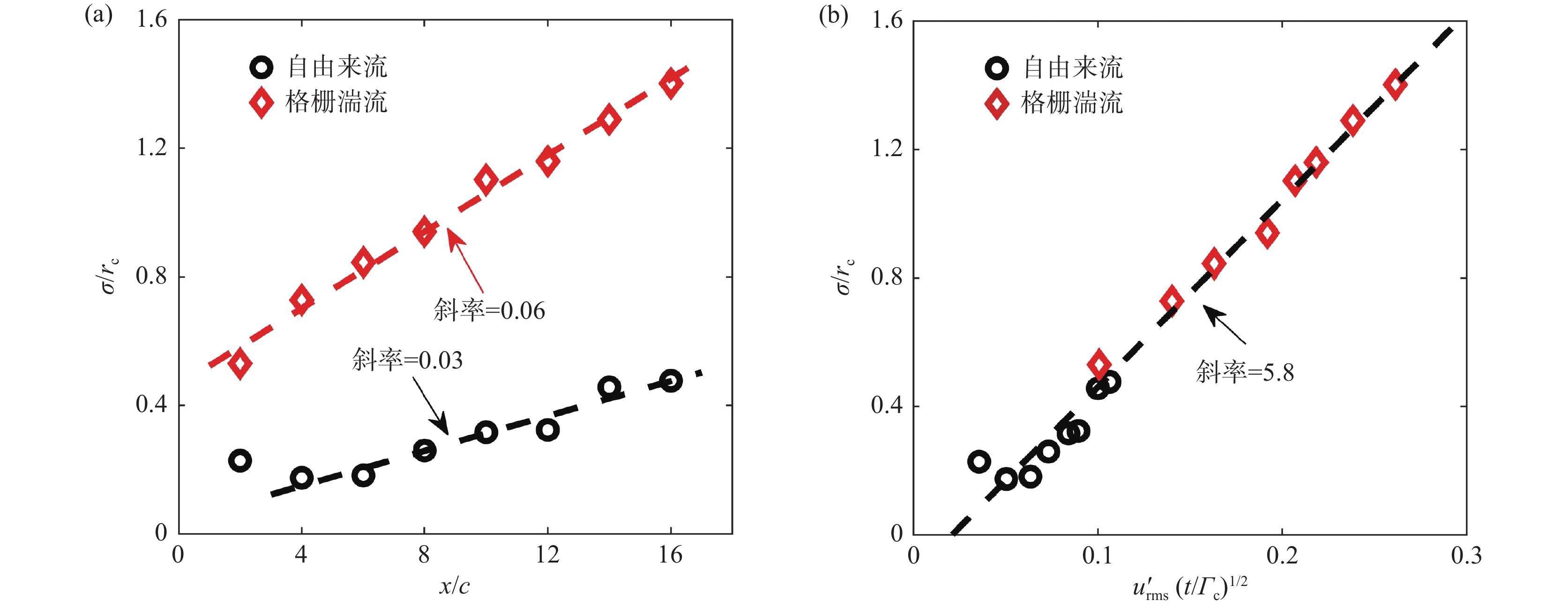
翼尖涡的不稳定摇摆运动随着翼尖涡向下游的演化而发展^[26]，本小节定量分析摇摆运动幅值的沿程演化。图7（a）展示了x/c = 2～16流向范围内翼尖涡摇摆运动幅值随流向位置的变化。可以看到随流向距离的增加，摇摆运动幅值近似线性增大。在x/c = 2处，摇摆幅值可能受到尾迹及二次涡结构^[27]的影响而在一定程度上偏离线性规律。此外，在格栅湍流的作用下，翼尖涡摇摆运动幅值显著增大且表现出更快的增长速率。

图  7  摇摆运动演化规律：(a) 摇摆幅值沿程演化，(b) 摇摆幅值标度规律

Figure  7.  The evolution of vortex wandering: (a) streamwise evolution and (b) scaling law of the wandering amplitude

下载: 全尺寸图片 幻灯片

进一步地，图7（b）给出了本实验中摇摆运动幅值的标度规律，其中特征时间$t = (x - 0.5c)/{U_\infty }$，表征翼尖涡自翼尖后缘拖出后在流动中发展的时间，${{\boldsymbol{u}}'_{{\mathrm{rms}}}}$为对应流向位置处来流的脉动速度均方根值，${\varGamma _{\mathrm{c}}}$为涡核半径区域内部的环量。可以看到不同来流湍流度下的翼尖涡摇摆运动能够较好地符合该标度规律，这在一定程度上说明了翼尖涡摇摆运动机理与来流湍流度的相关性。值得注意的是，该标度规律在形式上与Taylor^[28]推导的均匀各向同性湍流中被动标量的扩散规律非常相似。在Taylor经典的湍流扩散理论中，被动标量位置的标准差满足$\sigma$ ～ ${{\boldsymbol{u}}'_{{\mathrm{rms}}}}{(t{{T}})^{1/2}}$，其中特征时间${{T}}$为湍流积分时间尺度。若将特征时间以翼尖涡翻转时间$r_{\mathrm{c}}^2/{\varGamma _{\mathrm{c}}}$代入，即可得到翼尖涡摇摆运动标度规律${\sigma \mathord{\left/ {\vphantom {\sigma {{r_c}}}} \right. } {{r_{\mathrm{c}}}}}$ ～ ${{\boldsymbol{u}}'_{{\mathrm{rms}}}}{(t/{\varGamma _{\mathrm{c}}})^{1/2}}$。该式说明翼尖涡摇摆运动和翼尖涡旋转过程中对环境湍流中小尺度涡丝的卷吸与动量交换可能存在关联，但摇摆运动的一般性机理仍有待进一步研究。

2.2.3   翼尖涡统计量演化规律

翼尖涡涡核半径及切向速度峰值作为两个重要的物理量，与翼尖涡所影响的危险区域紧密相关，常被用于尾迹遭遇风险的评估^[29]。本小节主要对时间平均及系综平均得到的翼尖涡涡核半径及切向速度峰值的沿程演化规律进行分析。

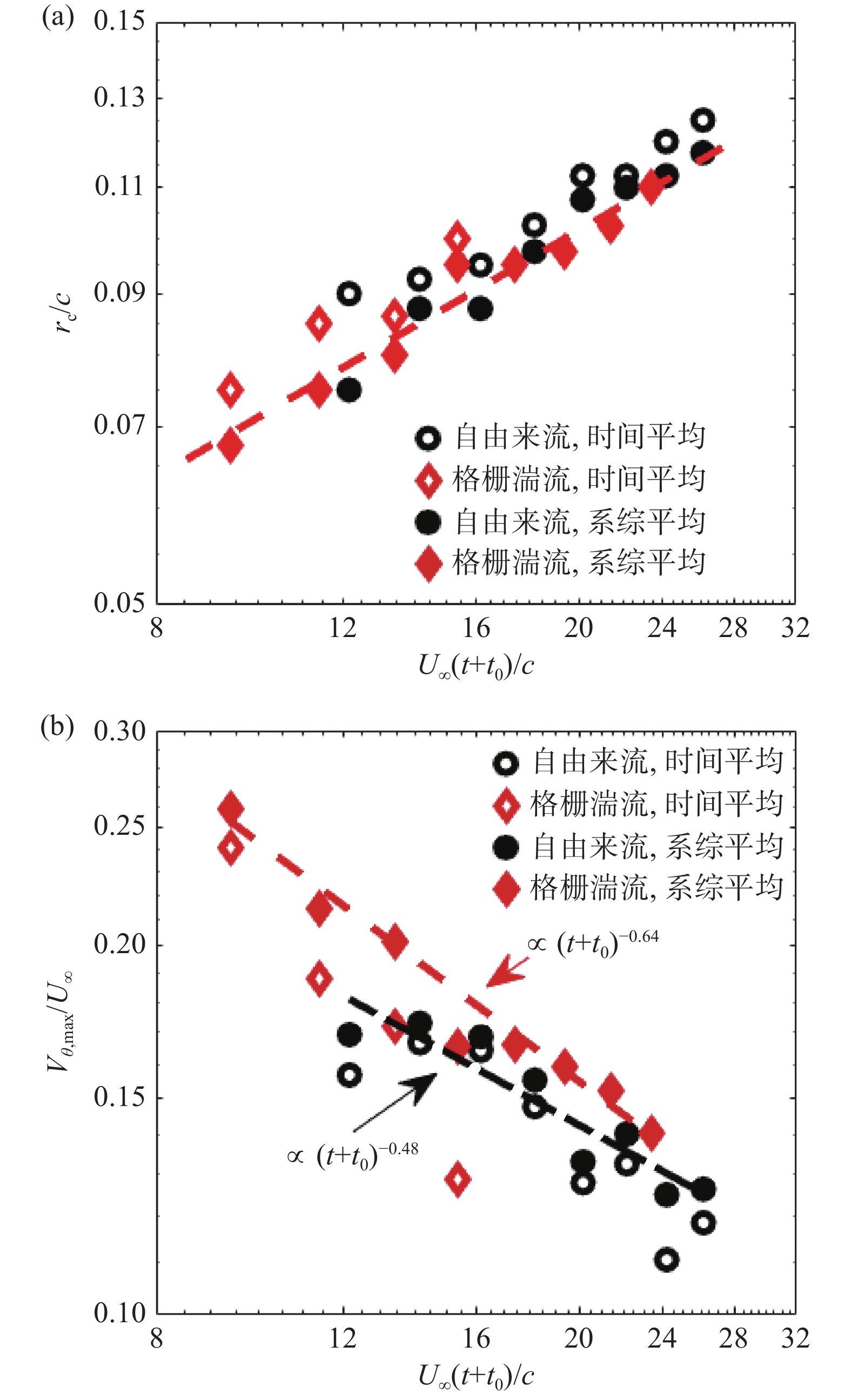
图8（a）展示了时间平均与系综平均得到的涡核半径结果。可以看到时间平均方法对所有对应流向站位处的涡核半径都有不同程度的高估。格栅湍流条件下，x/c > 8之后的流向站位，由于摇摆运动强烈的“抹平”效应已经无法从时间平均流场中得到涡核半径及速度峰值等信息，故这里仅给出了x/c ≤ 8的时间平均结果。涡核在向下游发展过程中不断外扩，理论上对于理想线涡模型，其黏性扩散应当满足${r_{\mathrm{c}}} \propto \sqrt {\nu t}$^[30]。在本实验中，可以通过类似的规律描述不同来流条件下的涡核半径演化，即：

图  8  涡核半径及切向速度峰值沿程演化规律：（a）涡核半径，其中直线为系综平均数据通过式（7）拟合的结果,（b）切向速度峰值，其中直线为系综平均数据拟合结果

Figure  8.  Streamwise evolution of core radius and peak tangential velocity: (a) core radius, the line corresponds to the fitting results of ensemble averaging data using Eq. (7), (b) peak tangential velocity, the lines corresponds to the fitting results of ensemble averaging data

下载: 全尺寸图片 幻灯片

其中，t₀为虚拟时间原点。自由来流和格栅湍流条件下，基于系综平均的涡核半径及其对应的拟合结果如图8（a）所示，对于自由来流条件，t₀ = 6.56 s；对于格栅湍流条件，t₀ = 4.65 s。可以发现，式（7）在不同来流条件下均能较好地描述系综平均涡核半径的演化，说明在实验参数空间内，湍流度对涡核的扩散行为没有显著影响。也就是说，不同来流条件下翼尖涡的涡核均表现出黏性扩散为主导的增长规律，尚未发生高湍流度下翼尖涡的快速破碎机制^[31]。

图8（b）展示了不同流向站位处的切向速度峰值结果，可以看到时间平均方法显著低估了对应位置处的切向速度峰值，对于格栅湍流条件下的实验结果尤为如此。对于系综平均结果，注意到${\varGamma _{\mathrm{c}}} = 2{\text{π}} {V_{\theta ,\max }}{r_{\mathrm{c}}}$，通过翼尖涡完全卷起后涡核内部环量${\varGamma _{\mathrm{c}}}$与式（7）拟合得到的涡核半径，可建立切向速度峰值衰减模型，如式（8）所示：

从图8（b）可以发现，对于系综平均结果，自由来流条件下的切向速度峰值的衰减规律与式（8）较为一致；而格栅湍流下，翼尖涡切向速度峰值的衰减速率更快。考虑到涡核保持黏性扩散，这一现象可能来源于涡剥离机制^[8]，但在下游随着格栅湍流的衰减这一影响也相对减弱，进一步验证了实验参数空间内黏性扩散为主导的翼尖涡衰减规律。

3.   结　论

本文通过时间解析的SPIV技术测量了自由来流及格栅湍流条件下孤立翼尖涡的速度场，测量范围覆盖机翼模型后x/c = 2～16的流向站位。首先分析了翼尖涡的摇摆运动特点与演化规律，通过系综平均方法消除摇摆运动对统计量测量结果的影响，得到了修正后的流场结果，在此基础上对翼尖涡涡核半径及切向速度峰值的沿程演化规律进行分析，取得了如下结论：

1） 孤立翼尖涡的不稳定摇摆运动在向下游发展过程中幅值沿流向近似线性增长。在格栅湍流作用下摇摆运动幅值显著增强，同时不同来流条件下摇摆运动幅值可由来流脉动速度标度。

2） 翼尖涡的摇摆运动对翼尖涡统计量的计算有显著的“抹平”效应。格栅湍流条件下其影响进一步增强，以至于在下游站位处无法从时间平均数据中获得翼尖涡的有效信息。在实验中有必要采取系综平均方法以恢复流场的真实信息。

3） 在本实验参数空间内，自由来流及格栅湍流条件下翼尖涡均表现为黏性扩散为主导的衰减行为。涡核半径服从统一的黏性增长规律，格栅湍流下的翼尖涡切向速度峰值衰减相对更快，但尚未表现出明显的高湍流度下翼尖涡的快速破碎机制。

本研究针对孤立翼尖涡进行了深入探讨。然而，在实际飞机尾流环境中，涡系之间存在着相互作用和诱导效应。鉴于此，本团队在后续工作中，将研究在来流湍流度影响下对转涡对的演化特性和涡系不稳定性的作用机制。