Skin friction measurement and drag reduction of porous media under cryogenic and high Reynolds number conditions
-
摘要:
为研究低温高雷诺数条件下多孔介质湍流减阻规律及雷诺数效应，在0.3 m低温连续式风洞开展了壁面摩擦阻力测量及多孔介质减阻试验。分别在光滑平板和多孔介质区域下游布置低温脉动压力传感器和油流，对脉动压力功率谱及下游全局摩擦阻力进行测量。结果表明：摩擦阻力系数随雷诺数的增大而减小；多孔介质减阻率随雷诺数的增大（增大马赫数或降低来流总温），呈无固定规律下降趋势，且多孔介质的引入，使下游脉动压力的低频信号强度增加，高频信号强度减弱；在马赫数Ma = 0.300、雷诺数Re = 7.51×106、来流总温T0 = 140 K这一典型工况下，多孔介质仍具有11.4%的减阻率，初步验证了在低温高雷诺数条件下使用多孔介质减阻控制策略的可行性。
Abstract:To investigate the drag reduction laws and the Reynolds number effects of porous media under cryogenic and high Reynolds number conditions, this study conducted skin-friction measurements and drag reduction experiments in a 0.3 m transonic cryogenic wind tunnel. Pressure sensors and oil flow devices were installed downstream of the smooth plate and porous media region respectively, to measure the power spectra of fluctuating pressure and the global skin friction. It is shown that the skin friction coefficient decreases with the increase of Reynolds number. With the increase of Reynolds number (increasing the Mach number or decreasing the total temperature of the incoming flow), the porous media drag reduction ratio shows a non-uniform decreasing trend. Besides, the introduction of porous media, the low-frequency signal strength of the downstream pulsating pressure increases, and the intensity of the high-frequency signal is weakened. Under the typical condition that Mach number Ma = 0.300, Reynolds number Re = 7.51×106 and the total temperature of the incoming flow T0 = 140 K, the drag reduction ratio of porous media is 11.4%, which initially verifies the feasibility of the drag reduction control strategy under low temperature and high Reynolds number conditions.
-
0. 引 言
湍流是流体力学尚未完全解决的世界性难题[1]。在研究湍流边界层时，无论是考核湍流理论研究还是检验数值模拟结果，壁面摩擦阻力是最能说明问题的一个指标[2]。真实飞行条件下，飞机所受的摩擦阻力占总阻力的50%以上，因此，降低湍流边界层中的摩擦阻力对提高飞机航程、增大有效载重、降低燃油消耗等具有重要意义。湍流边界层减阻的首要工作是对壁面摩擦阻力进行精确测量。然而，壁面摩擦阻力值量级较小（10–3），实现其精确测量具有很大挑战。目前，国内外学者已提出了多种测量方法[3-5]，如压降法、平均速度法、Preston 管法、油膜法、壁面热线法、热膜法以及基于浮动平板的测力天平法等，其中油膜法被广泛认为是测量时均壁面摩擦阻力最精确的方法之一。
湍流边界层减阻控制手段分为主动控制和被动控制两种。被动控制相较于主动控制不需要外界输入能量，所施加的控制或干扰固定不变，成本较低且应用便捷，Duraisamy等[6]认为：“即使是最先进的航空工业也会继续看好和采用传统的、安全的、简单的被动控制技术实现湍流减阻”。被动控制最初的研究重点主要放在减小表面粗糙度上，直到20世纪70年代，兰利研究中心发现沟槽表面能够减小表面摩擦阻力（也称摩阻），突破了表面越光滑阻力越小的传统思维[7]。壁湍流的相干结构与湍流的高摩阻关系密切，通过对壁面相干结构施加影响以减小湍流摩擦阻力成为湍流减阻研究的主要思路。1994年，Choi等[8]使用直接数值模拟（direct numerical simulation, DNS ）方法，通过在壁面施加相反的法向速度避免了与雷诺应力产生相关的近壁猝发事件，实现了25%的减阻效果。邓冰清[9]基于条带瞬态增长产生流向涡的机理进一步研究了反向控制对近壁区湍流自维持机制的影响，并提出了加强的反相控制和减弱的同相控制，将最大减阻率从25%提升到了34%。Li等 [10]利用高分辨率粒子图像测速法（particle image velocimetry, PIV）对平板涂层近壁流场进行了测量，发现减阻是通过改变流体与表面之间的相互作用（即滑移特性）以及调整湍流结构来实现的，并且随着雷诺数的增加，减阻和滑移性能都有所提高。Rosti等[11]和Du等[12]利用多孔壁面分别获得了20%和43.7%的减阻效果。Klausmann与Ruck[13]在雷诺数3×104～1.4×105 区间，对背风侧覆盖多孔介质的圆柱绕流进行了风洞试验，发现阻力系数可降低 7.7%～13.2%。
以上减阻研究主要集中在中低雷诺数范围，而现代飞行器尺寸大、巡航雷诺数高，中低雷诺数减阻研究已不能满足目前的工程应用需求，高雷诺数条件下的减阻控制研究显得愈发重要。但目前雷诺数对减阻的影响仍处于初步研究阶段，特别是基于近壁相干结构的控制方案在高雷诺数湍流减阻应用上还存在很大挑战[14]，大多数研究还停留在数值模拟阶段。Gómez等 [15]在高雷诺数条件下进行直接数值模拟时发现，顺流优先的可渗透基材料的最大阻力系数减少约20%～25%。Rastegari与Akhavan [16] 同样利用DNS技术研究了高雷诺数湍流中超疏水表面的减阻特性，发现对于给定几何形状和表面微结构尺寸，减阻效果随雷诺数的增大而降低。随着计算能力的提升和实验技术的革新，对高雷诺数下的减阻研究逐步深入，发现壁湍流在内外区间存在复杂的相互作用，表现出不同的流动现象和规律，这也是高雷诺数壁湍流减阻研究的关键和难点[17] 。
近年来，随着NTF（National Transonic Facility）和ETW（European Transonic Wind Tunnel）这两座大型低温高雷诺数风洞设备技术体系的逐步完善，高雷诺数壁湍流减阻逐渐成为国际湍流研究的热点。欧美依托洁净天空（Clean Sky）等重大研究计划对高雷诺数减阻控制及其机理进行了探索[18-19]，目前，已初步完成了风洞试验与飞行试验验证。
本文依托中国空气动力研究与发展中心0.3 m低温连续式风洞，发展低温油流试验技术，开展高雷诺数条件下壁面摩擦阻力测量和壁湍流减阻研究，并对其雷诺数效应进行初步探索，为我国大型低温风洞试验技术体系建设提供技术参考，并为高雷诺数减阻研究提供思路。
1. 摩擦阻力测量原理
1.1 油膜干涉法
油膜干涉法测量的基础原理是Squire推导的油膜方程[20]，核心是测量条纹宽度来计算油膜厚度，进而解算壁面摩擦阻力，主要求解公式如下：
∂h∂t=−12μ∂(τwh2)∂x (1) h=λ∅4π(1√n20−sin2θi) (2) 式中：h为油膜厚度；t为时间；μ为硅油的黏性系数；x为距离；τw为壁面摩擦阻力；λ为单色光波长；∅为条纹级数；n0为硅油折射率；θi为光线入射角。由此可得壁面摩擦阻力系数：
Cf=2n0cosθkΔx∅λ∫t2t1q∞(t)μ(t)dt (3) 式中：θk为光线折射角；Δx为∅级条纹宽度；q∞为来流动压。
1.2 荧光油流法
荧光油流法综合了荧光油流技术与光学流动技术[21]，同油膜干涉法一样，其基础原理也是油膜方程，但其测量范围更大且空间分辨率更高，可以得到全局摩擦阻力场。其求解公式如下：
g=I(x1, x2)Ies(x1, x2)=ah(x1, x2) (4) τi=ag−1ui=0.5ρ∞U2∞Cf (5) 式中：g是灰度；I(x1,x2)是荧光粒子在紫外光源激发下发出的光强分布；Ies(x1,x2)是荧光粒子在模型表面的紫外光强分布；a=2μ/(βk)为绝对摩擦阻力与相对摩擦阻力的比例系数，其中，β为物平面与像平面的比例系数，k为油膜厚度与灰度的线性比例系数，同一车次试验中a值处处相等；ui为油膜在成像平面上的像素运动速度；g−1ui为相对摩擦阻力；Cf为摩擦阻力系数；U∞为来流速度，ρ∞为来流密度。
受限于现有光学试验测试条件，本次荧光油流试验未对油膜厚度进行标定。考虑到油膜干涉法可定量测量局部摩擦阻力，本次试验将结合以上两种测试方法，首先利用油膜干涉法测量测试区域表面出现干涉条纹位置处的绝对摩擦阻力，然后利用荧光油流法获取相同来流工况下测试区域全局相对摩擦阻力分布，即可得到绝对摩擦阻力与相对摩擦阻力的比例系数a，进而获得全局绝对摩擦阻力的分布情况。
2. 试验系统方案
2.1 风洞及试验设备
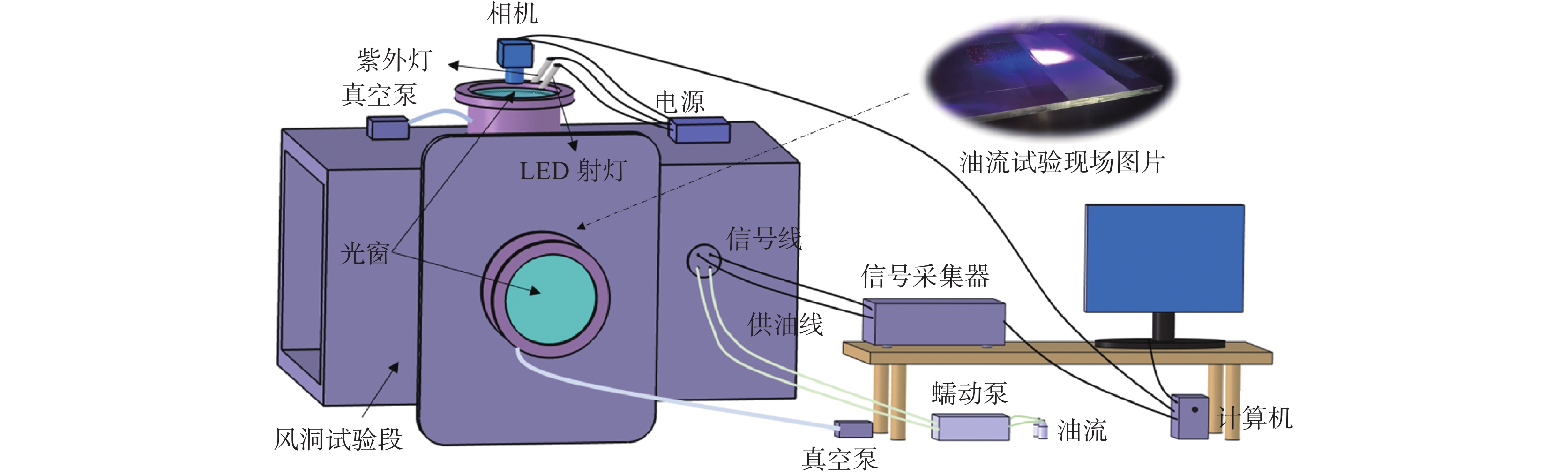
试验在中国空气动力研究与发展中心0.3 m低温连续式风洞中开展。该风洞通过液氮喷射段向洞内喷入液氮，然后汽化吸热实现低温运行。稳定段总压范围为0.2×105～4.5×105 Pa，总温范围为110～323 K，马赫数范围为0.150～1.300，湍流度低于0.3%，试验段尺寸为325 mm（宽）×275 mm（高）。整个风洞试验系统图如图1所示。
油膜干涉试验光源使用波长为460 nm、功率为45 W的无频闪单色LED射灯；荧光油流试验使用波长为400 nm、功率为20 W并可实现10%～100%连续调光的紫外灯源，能为荧光油流提供满足吸收光谱的稳定激发光和照明视场；采用的CCD相机型号为FASTCAM Mini AX100，分辨率为
1 048 pixel ×1 048 pixel，另外为防止杂光干扰，相机镜头加装了600 nm的截止高通滤波片，试验中相机拍摄帧率设置为2000 帧/s。脉动压力传感器选用Kulite绝压型CCQ-062系列，其工作温度范围为80～393 K，压力量程为2 ×105 Pa，外径为1.7 mm。数据采集选用东华DH8300N，采集频率为10 kHz。试验过程中固定来流总压为105 kPa。
2.2 试验模型
试验采用平板为基础研究模型，整体设计如图2所示。模型尺寸设计为400 mm（长）×315 mm（宽）×10 mm （厚），为减少流动分离，前缘加工成25°斜劈。为保证测试区域达到充分的湍流状态，在平板前缘附近布置了一根直径为5 mm的拌线。为便于对比研究多孔介质湍流减阻特性，同时保持试验来流一致性，减少试验误差，在距离平板前缘100 mm且紧靠平板中轴线处对称设计多孔介质和光滑区域，多孔介质区域大小为100 mm（长）×100 mm（宽）×9 mm（高）。平板上各部分的相对位置如图3所示。所选用的多孔介质为泡沫铜材料（孔隙率97%，孔密度20 PPI），主要由固体铜制骨架及其分割形成的空间孔隙组成。布置多孔介质需要在平板上预留凹槽，为保证上表面与平板表面平齐，凹槽设计尺寸与多孔介质尺寸相同，凹槽下壁板厚度设置为1 mm，既能起到固定多孔介质的作用又可以阻挡平板下部气流上窜到多孔介质控制区域。在多孔介质和光滑区域下游相同位置处分别预留了一个低温脉动压力传感器安装孔。
2.3 油流试验设计
由于风洞从启动到稳定运行所需时间相对较长（2 h左右），且稳定过程中来流马赫数Ma = 0.1，常规风洞中预先在模型表面刷油的技术方案在该低温风洞中不再适用。因此，本次试验采用外部供油方式，即在多孔介质下游1 mm处设置了一个供油槽（宽2 mm，深2 mm），槽内两个2 mm的圆孔分别嵌入特氟龙耐低温供油软管，软管引至风洞外与地面供油蠕动泵相连，同时平板尾部预留了宽60 mm的集油槽以减小油流对风洞的污染。模型采用低温304L钢材，由于油膜干涉法对模型表面光洁度有很高要求，因此对油流测试区域进行了镜面抛光处理，光洁度Ra为0.8 μm。
常规硅油凝固点一般在250 K左右，在低温风洞中，由于来流总温较低导致其无法适用。Manfrost SF-1是基于高性能含硅聚合物的特殊配方的液相硅油，在超低温环境下仍具有良好的流动性。为检验在该硅油中添加一定比例的荧光粉后是否仍具有良好的耐低温性能，本文将调配好的荧光油剂放入140 K低温试验箱内进行验证，连续冷冻24 h后，通过低温箱内玻璃棒搅拌发现荧光油剂流动性良好。
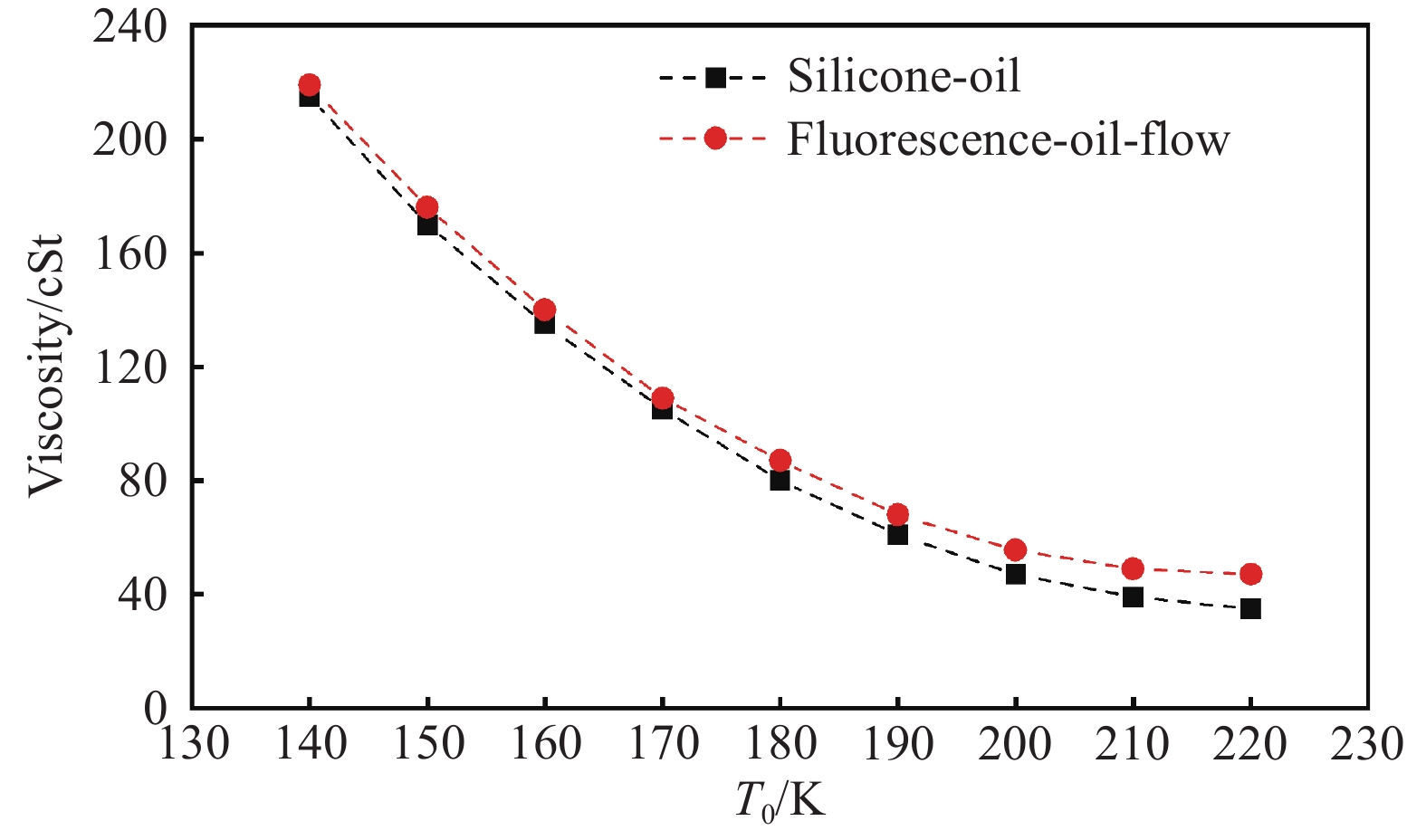
在完成荧光油剂低温流动性能测试后，利用低温黏度分析仪器测试了纯硅油和调配的荧光油剂在140～220 K范围内的黏度大小，测试结果如图4所示，图中纵轴单位1 cSt = 1 mm2/s。由图可知，本试验中所调配的荧光油剂黏度比纯硅油略大，随着温度降低，二者的黏度差异变小，说明本试验中调配的荧光油剂在低温下具有良好的流动性能，且其性能接近于纯硅油，达到了预期的低温应用要求。
3. 试验结果及讨论
3.1 典型工况摩阻测量结果
图5（a、b）分别为利用油膜干涉法和荧光油流法拍摄得到的工况T0 = 140 K、Ma = 0.300下光滑平板表面油流原始图像，从图中可清晰地看出条纹分布情况以及荧光油流流动波纹，这保证了图像后处理的准确度。
![]()
图 5 光滑平板表面油流原始图像（T0 = 140 K, Ma = 0.300）Figure 5. Original images of oil flow on a smooth flat surface（T0 = 140 K, Ma = 0.300）表1和表2分别给出了利用油膜干涉法测量的光滑平板表面和铺设多孔介质平板表面在不同工况下的摩擦阻力系数，其中选取的流向位置是干涉条纹的中心位置，即：
ˉx=xstart+xend2 (6) 其中：xstart、xend分别为图像后处理过程中选取的干涉条纹流向方向开始和结束位置，为保证测量结果的准确性，二者距离不宜过大，距离为4～6条条纹最佳。
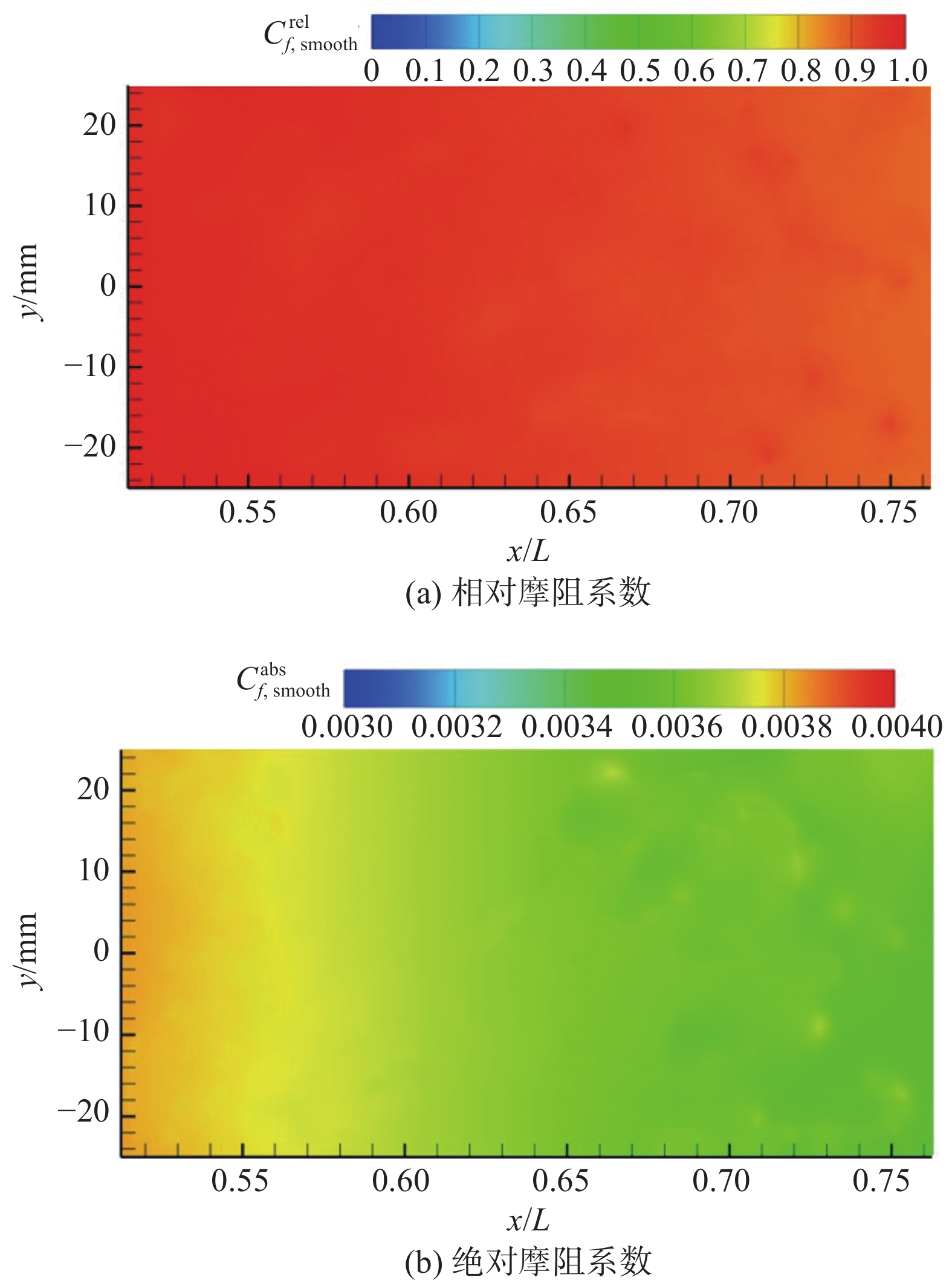
表 1 油膜干涉法测量的光滑平板表面摩擦阻力系数Table 1. Skin friction coefficient of a smooth flat surface measured by oil film interferometryMa T0/K ˉx /mm Cf,smooth/10–3 Cf,theory/10–3 误差/% 0.150 140 252 4.186 3.917 6.87 180 260 4.403 4.179 5.36 220 228 4.826 4.530 6.53 0.225 140 264 3.782 3.587 5.44 180 252 4.067 3.887 4.63 220 272 4.233 4.042 4.73 0.300 140 248 3.658 3.440 6.34 180 232 3.942 3.743 5.32 220 256 4.063 3.876 4.82 表 2 油膜干涉法测量的多孔介质平板表面摩擦阻力系数Table 2. Skin friction coefficient of a porous media-coated flat surface measured by oil film interferometryMa T0/K ˉx/mm Cf,porous/10–3 0.300 140 248 3.227 180 232 3.538 220 256 3.769 通过表1可发现，使用油膜干涉法测量的摩阻系数略大于理论值Cf,theory，出现这种结果的原因可能是模型表面存在一定的粗糙度或者油膜发展不够均匀，但总体来看与理论值的相对误差基本在 5% 左右。图6（a）为利用荧光油流法得到的对应工况下光滑平板表面相对摩擦阻力系数云图。将表1中T0=140 K、Ma=0.300、ˉx=248 mm处的油膜干涉法测得的Cf,smooth=3.658×10–3带入荧光油流法测得的相对摩擦阻力结果，可得到相同来流工况下平板表面绝对摩擦阻力系数分布情况，如图6（b）所示。后续荧光油流法摩擦阻力系数后处理均利用表1和表2中的数据进行计算。
![]()
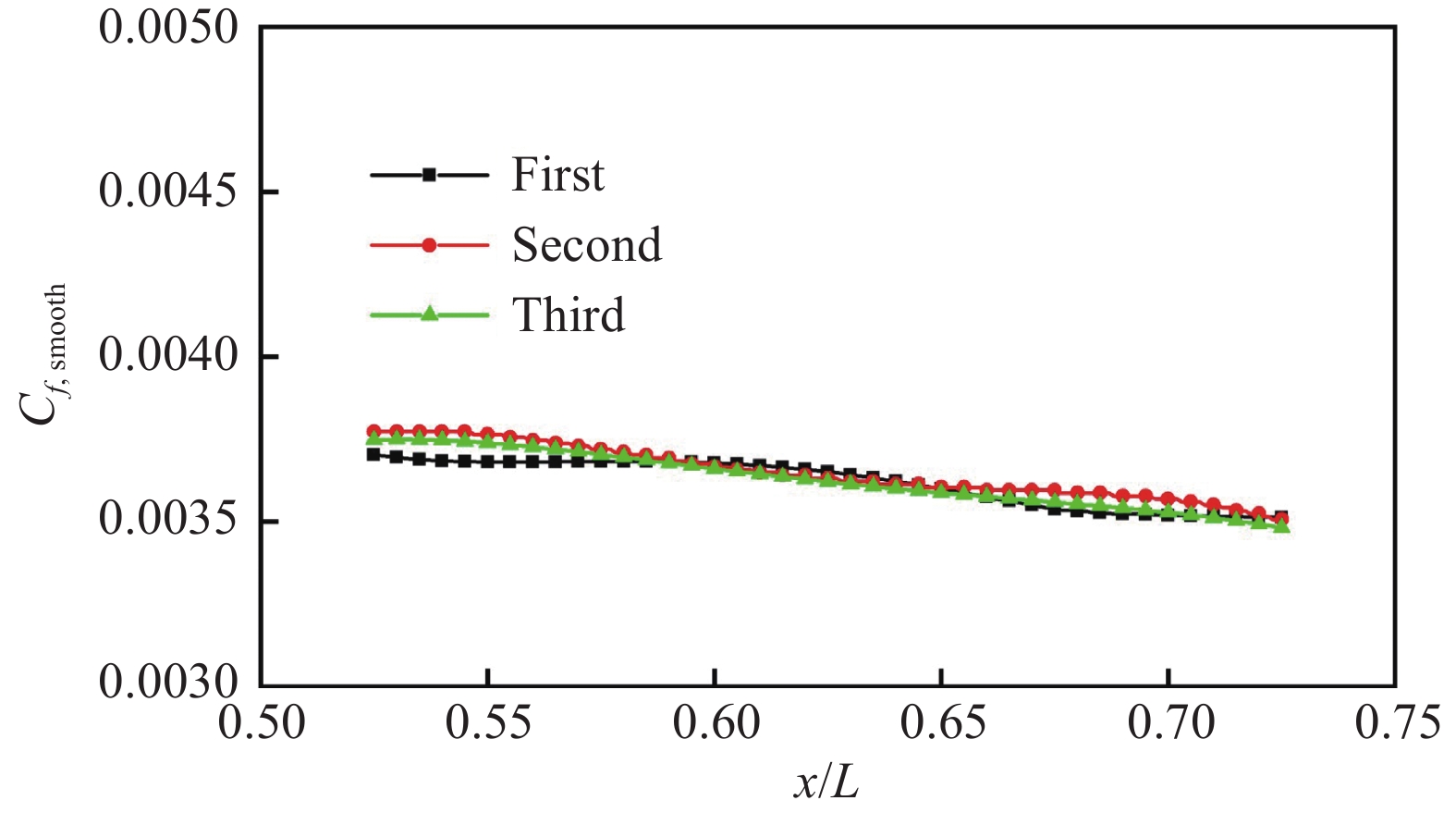
图 6 光滑平板表面摩阻系数分布云图（T0 = 140 K, Ma = 0.300）Figure 6. Contour of skin friction coefficient on a smooth flat surface（T0 = 140 K, Ma = 0.300）图7给出了光滑平板在来流总温T0 = 140 K，马赫数Ma = 0.300这一工况下连续测量3次得到的典型流向站位（x/L = 0.525～0.725）摩擦阻力系数曲线。从图中可看出，3次测量结果吻合较好，重复精度低于4.5%，说明本试验所使用的测试系统是稳定可靠的。
![]()
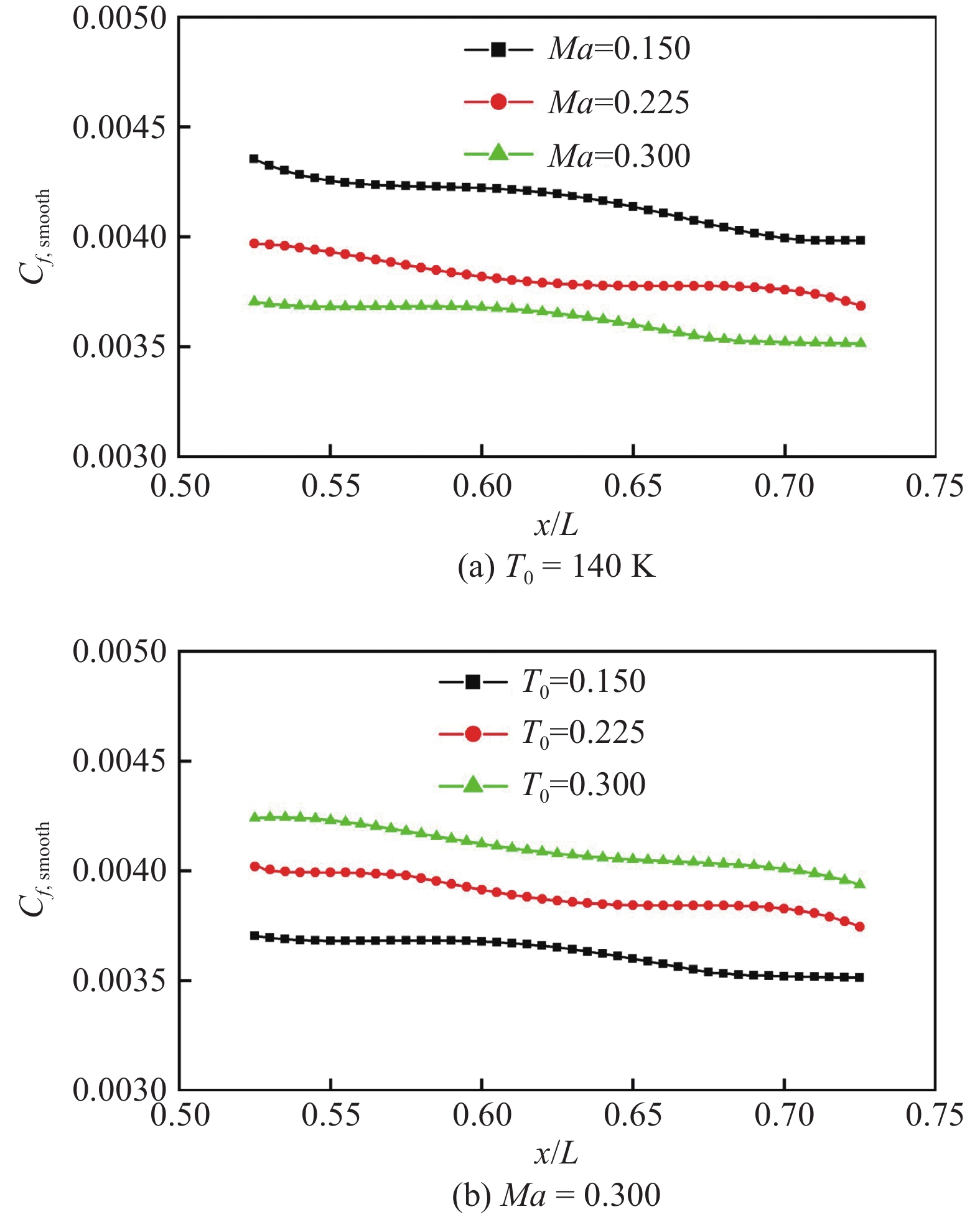
图 7 相同工况下 3 次测量提取的摩阻系数曲线Figure 7. Skin friction coefficient curves extracted from three measurements under the same test conditions图8（a）给出了在固定来流总温T0 = 140 K时，来流马赫数Ma分别为0.150、0.225、0.300这3种工况下光滑平板表面摩擦阻力系数分布云图；图8（b）给出了固定来流马赫数Ma = 0.300时，来流总温T0分别为140、180、220 K（对应的平板特征雷诺数Re分别为7.51×106、5.25×106、3.99×106）这3种工况下光滑平板表面摩擦阻力系数分布云图。
![]()
图 8 不同来流参数下光滑平板表面摩阻系数分布云图Figure 8. Contour of skin friction coefficient on a smooth flat surface with different incoming flow parameters图9（a、b）是根据光滑平板表面摩擦阻力系数云图提取的典型流向站位摩擦阻力系数曲线。从图9（a）可以看出，光滑平板表面摩擦阻力沿流向方向逐渐减小，并且随来流马赫数的增大（Re增大），对应的摩擦阻力系数减小，与经典湍流理论一致[22]。从图9（b）可以得出与图9（a）相似的结论，随来流总温的降低（Re增大），对应的摩擦阻力系数减小。
![]()
图 9 根据摩擦阻力云图提取的摩擦阻力系数曲线Figure 9. Curves of skin friction coefficient extracted from contour图10给出了3个不同流向站位的摩擦阻力系数随雷诺数的变化曲线。由图可看出：摩擦阻力系数与雷诺数的曲线斜率是随机的，在相同马赫数及流向站位下，如Ma = 0.300，x/L = 0.625处的摩擦阻力系数在Re = 3.99×106时为4.08×10–3，而在Re = 7.51×106时为3.65×10–3，约下降10.5%，说明光滑平板表面摩擦阻力分布存在显著的雷诺数效应，且雷诺数对其的影响是非线性的。
![]()
图 10 不同流向站位摩阻系数随Re变化曲线Figure 10. Variation of skin friction coefficient with Reynolds number at different flow stations3.2 摩擦阻力控制效果及讨论
为了研究多孔介质的减阻效果，定义减阻率为：
η=Cf,smooth−Cf,porousCf,smooth×100% (7) 其中：Cf,smooth和Cf,porous分别表示光滑表面和多孔介质表面下游区域摩擦阻力系数。
图11（a～c）分别给出了来流马赫数Ma = 0.300时，平板特征雷诺数Re分别为3.99×106、5.25×106、7.51×106三种工况下铺设多孔介质平板和光滑平板下游的摩擦阻力系数对比云图，图中白色虚线上、下分别为铺设多孔介质平板和光滑平板下游荧光油流测试区域。从图中可以看出，起始摩擦阻力系数分布不对称，这可能是由于多孔介质的展向作用影响了相邻光滑平板表面下游流动。
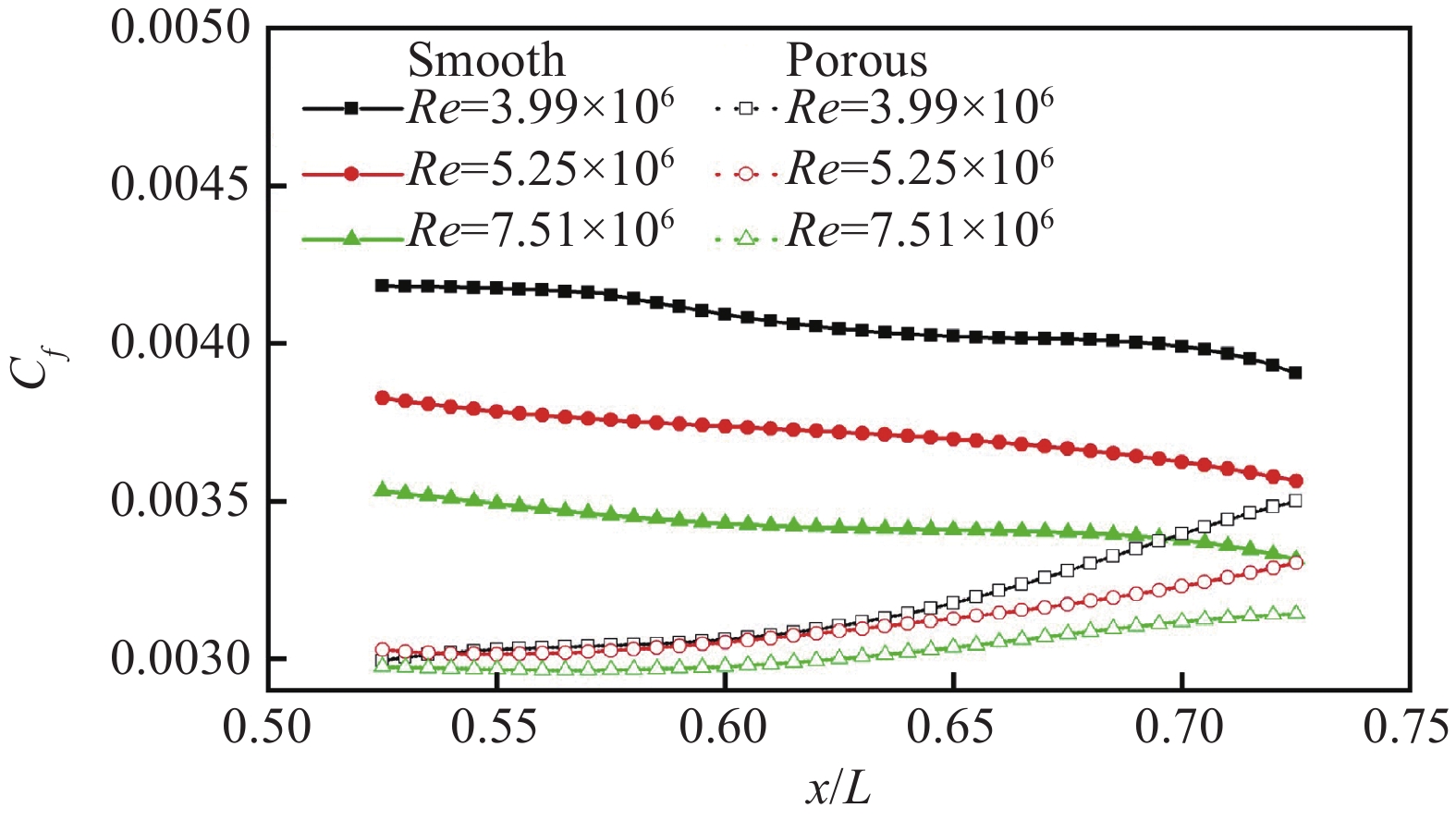
根据摩擦阻力系数云图提取典型流向站位的摩擦阻力系数时，由于多孔介质对下游展向方向的流动有一定的影响，因此在光滑表面提取摩擦阻力系数时需尽可能剔除多孔介质影响的区域，同时，为便于对比，在图11（a～c）的两个白色虚线框内分别进行数据提取，提取后的摩擦阻力系数对比曲线如图12所示，图中实心点、空心点曲线分别代表光滑平板和铺设多孔介质平板的摩擦阻力系数。
![]()
图 12 根据摩擦阻力云图提取的摩擦阻力系数对比曲线（Ma = 0.300）Figure 12. Comparison of skin friction coefficients extracted from contour (Ma = 0.300)从图12可以看出，相较于光滑平板，铺设多孔介质平板下游摩擦阻力系数下降明显，说明多孔介质具有良好的湍流减阻性能。同时还可发现，铺设多孔介质平板的下游附近区域摩擦阻力分布与光滑平板呈现的规律相反，即沿着流向方向摩擦阻力系数逐渐增大。这可能是由于多孔介质改变了下游近壁面的流场结构，使得靠近壁面的速度梯度变得更加平缓，从而在初期时使得多孔介质平板下游区域摩擦阻力减小；然而，随着流体继续沿着表面流动，速度梯度因为多孔介质对近壁面流场控制作用的逐渐减弱而增加，导致摩擦阻力系数增大。
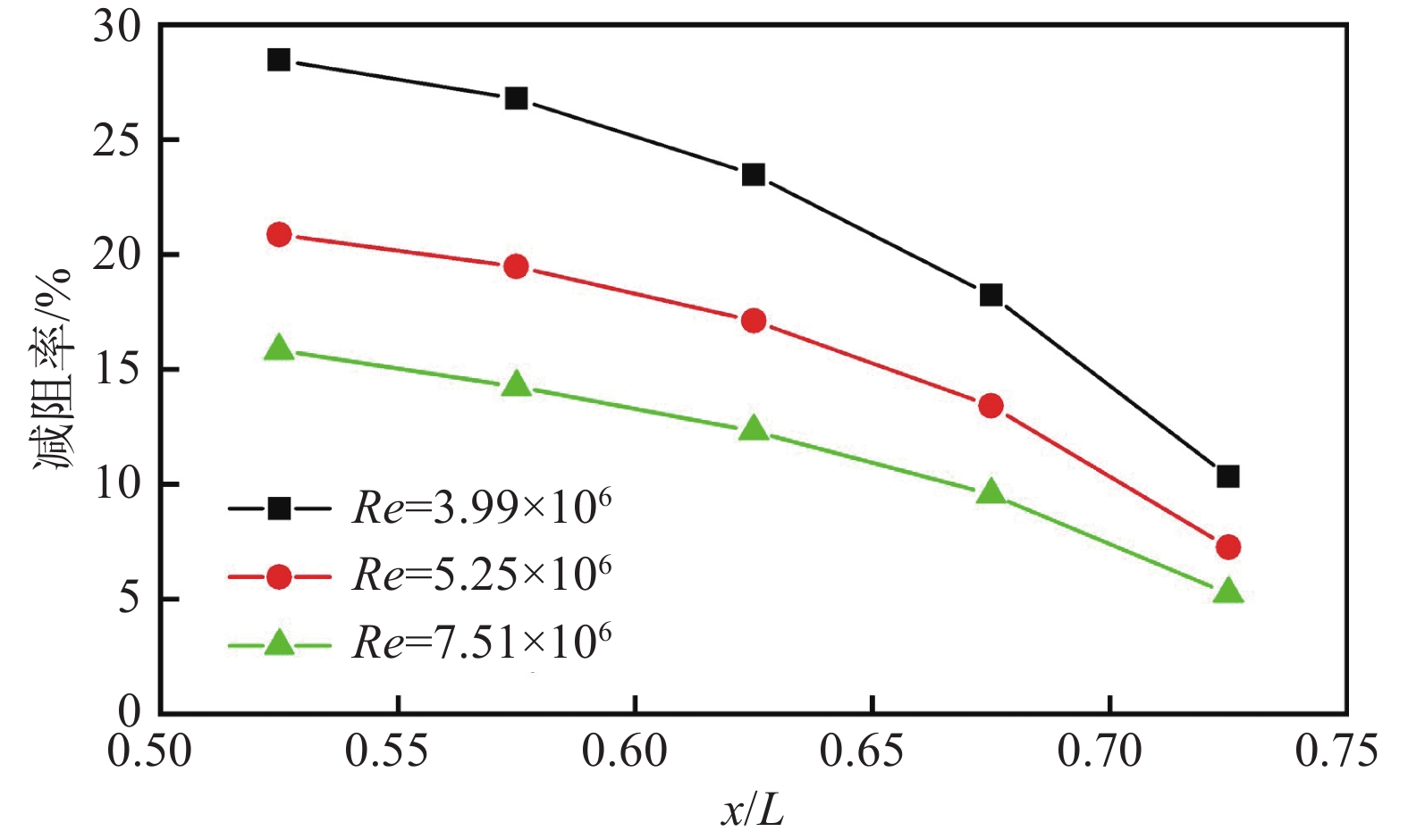
多孔介质减阻控制效果的雷诺数效应曲线如图13所示。从图中可以看出，随着流向距离增加，多孔介质减阻率大幅下降。同时还可以看出多孔介质的减阻效果随着雷诺数的增加而显著降低。在Ma = 0.300条件下，Re=3.99×106时，测试区域减阻率约为21.5%，而当Re=7.51×106时，减阻率约为11.4%。
![]()
图 13 多孔介质减阻控制效果的雷诺数效应（Ma = 0.300）Figure 13. Reynolds number effect on drag reduction control effectiveness of porous media (Ma = 0.300)图14为来流马赫数Ma = 0.300、来流总温T0 = 140 K这一工况下光滑平板与铺设多孔介质平板下游同一位置处脉动压力功率谱对比曲线，由图可知，铺设多孔介质后，低频信号强度增大，高频信号强度减小，这表明由于多孔介质的减阻作用，在功率谱图像上虽表现为一定程度上增加了低频能量，但同时吸收了更多的高频扰动。
4. 结 论
本文通过利用0.3 m低温连续式风洞可独立调节来流马赫数、来流总温、来流总压的优势开展了多孔介质在低温高雷诺数条件下减阻控制试验，得出如下结论：
1） 通过使用耐低温油剂，将荧光油流法和油膜干涉法相结合，可以较为精确地测量平板表面摩擦阻力分布情况，该方法是一种在深低温环境下较为可靠的表面摩擦阻力测量技术。
2） 深低温环境下平板表面摩擦阻力的分布与经典湍流理论一致，并且存在显著的非线性雷诺数效应。
3） 相比光滑平板，多孔介质有一定的减阻效果，随着雷诺数增大，多孔介质减阻率呈非线性下降趋势，并且减阻控制能力沿着流向方向逐渐减弱。
本次风洞试验未研究来流在压缩条件下模型表面的摩擦阻力分布情况和多孔介质减阻流动机理，下一步将开展宽马赫数范围低温试验，同时从流场角度探究高雷诺数条件下多孔介质对摩擦阻力控制的影响规律及机理。
-
![]()
图 5 光滑平板表面油流原始图像（T0 = 140 K, Ma = 0.300）
Figure 5. Original images of oil flow on a smooth flat surface（T0 = 140 K, Ma = 0.300）
![]()
图 6 光滑平板表面摩阻系数分布云图（T0 = 140 K, Ma = 0.300）
Figure 6. Contour of skin friction coefficient on a smooth flat surface（T0 = 140 K, Ma = 0.300）
![]()
图 7 相同工况下 3 次测量提取的摩阻系数曲线
Figure 7. Skin friction coefficient curves extracted from three measurements under the same test conditions
![]()
图 8 不同来流参数下光滑平板表面摩阻系数分布云图
Figure 8. Contour of skin friction coefficient on a smooth flat surface with different incoming flow parameters
![]()
图 9 根据摩擦阻力云图提取的摩擦阻力系数曲线
Figure 9. Curves of skin friction coefficient extracted from contour
![]()
图 10 不同流向站位摩阻系数随Re变化曲线
Figure 10. Variation of skin friction coefficient with Reynolds number at different flow stations
![]()
图 12 根据摩擦阻力云图提取的摩擦阻力系数对比曲线（Ma = 0.300）
Figure 12. Comparison of skin friction coefficients extracted from contour (Ma = 0.300)
![]()
图 13 多孔介质减阻控制效果的雷诺数效应（Ma = 0.300）
Figure 13. Reynolds number effect on drag reduction control effectiveness of porous media (Ma = 0.300)
表 1 油膜干涉法测量的光滑平板表面摩擦阻力系数
Table 1 Skin friction coefficient of a smooth flat surface measured by oil film interferometry
Ma T0/K ˉx /mm Cf,smooth/10–3 Cf,theory/10–3 误差/% 0.150 140 252 4.186 3.917 6.87 180 260 4.403 4.179 5.36 220 228 4.826 4.530 6.53 0.225 140 264 3.782 3.587 5.44 180 252 4.067 3.887 4.63 220 272 4.233 4.042 4.73 0.300 140 248 3.658 3.440 6.34 180 232 3.942 3.743 5.32 220 256 4.063 3.876 4.82 
下载: 导出CSV
表 2 油膜干涉法测量的多孔介质平板表面摩擦阻力系数
Table 2 Skin friction coefficient of a porous media-coated flat surface measured by oil film interferometry
Ma T0/K ˉx/mm Cf,porous/10–3 0.300 140 248 3.227 180 232 3.538 220 256 3.769
下载: 导出CSV
-
[1] GOLDSTEIN S . Fluid mechanics in the first half of this century[J]. Annual Review of Fluid Mechanics,1969 ,1 (1 ):1 −29 . doi: 10.1146/annurev.fl.01.010169.000245[2] 李鹏. 全局表面摩擦应力直接测量技术研究[D]. 南京: 南京航空航天大学, 2012. LI P. Studies of direct measurement techniques about global skin friction[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012 (in Chinese).
[3] TANNER L H, BLOWS L G . A study of the motion of oil films on surfaces in air flow, with application to the measurement of skin friction[J]. Journal of Physics E: Scientific Instruments,1976 ,9 (3 ):194 −202 . doi: 10.1088/0022-3735/9/3/015[4] BROWN J L, NAUGHTON J W. The thin-oil-film equation[R]. California: Ames Research Center, 1999. https://ntrs.nasa.gov/search.jsp?R = 19990047906
[5] DRIVER D M . Application of oil-film interferometry skin-friction measurement to large wind tunnels[J]. Experiments in Fluids,2003 ,34 (6 ):717 −725 . doi: 10.1007/s00348-003-0613-1[6] DURAISAMY K, SPALART P R, RUMSEY C L. Status, Emerging ideas and future directions of turbulence modeling research in aeronautics[R]. Langley Research Center, 2017. https://ntrs.nasa.gov/search.jsp?R = 20170011477
[7] WALSH M, WEINSTEIN L. Drag and heat transfer on surfaces with small longitudinal fins[C]// 11th Fluid and Plasma Dynamics Conference, Seattle, WA. Reston, Virginia: AIAA, 1978: 1161.
[8] CHOI H, MOIN P, KIM J . Active turbulence control for drag reduction in wall-bounded flows[J]. Journal of Fluid Mechanics,1994 ,262 :75 −110 . doi: 10.1017/s0022112094000431[9] 邓冰清. 基于相干结构的壁湍流减阻控制机理研究 [D]. 北京: 清华大学, 2014. DENG B Q. Research on the mechanism of wall turbulence drag reduction control based on coherent structure[D]. Beijing: Tsinghua University, 2014 (in Chinese).
[10] LI H Y, JI S S, TAN X K, et al . Effect of Reynolds number on drag reduction in turbulent boundary layer flow over liquid-gas interface[J]. Physics of Fluids,2020 ,32 (12 ):122111 . doi: 10.1063/5.0027727[11] ROSTI M E, BRANDT L, PINELLI A . Turbulent channel flow over an anisotropic porous wall–drag increase and reduction[J]. Journal of Fluid Mechanics,2018 ,842 :381 −394 . doi: 10.1017/jfm.2018.152[12] DU H, LI Q X, ZHANG Q L, et al . Experimental study on drag reduction of the turbulent boundary layer via porous media under nonzero pressure gradient[J]. Physics of Fluids,2022 ,34 (2 ):025110 . doi: 10.1063/5.0083143[13] KLAUSMANN K, RUCK B . Drag reduction of circular cylinders by porous coating on the leeward side[J]. Journal of Fluid Mechanics,2017 ,813 :382 −411 . doi: 10.1017/jfm.2016.757[14] 许春晓 . 壁湍流相干结构和减阻控制机理[J]. 力学进展,2015 ,45 (1 ):111 −140 . doi: 10.6052/1000-0992-15-006XU C X . Coherent structures and drag-reduction mechanism in wall turbulence[J]. Advances in Mechanics,2015 ,45 (1 ):111 −140 (in Chinese). doi: 10.6052/1000-0992-15-006[15] GÓMEZ-DE-SEGURA G, GARCÍA-MAYORAL R . Turbulent drag reduction by anisotropic permeable substrates–analysis and direct numerical simulations[J]. Journal of Fluid Mechanics,2019 ,875 :124 −172 . doi: 10.1017/jfm.2019.482[16] RASTEGARI A, AKHAVAN R . On drag reduction scaling and sustainability bounds of superhydrophobic surfaces in high Reynolds number turbulent flows[J]. Journal of Fluid Mechanics,2019 ,864 :327 −347 . doi: 10.1017/jfm.2018.1027[17] 郑晓静, 王国华 . 高雷诺数壁湍流的研究进展及挑战[J]. 力学进展,2020 ,50 (0 ):1 −49 . doi: 10.6052/1000-0992-19-009ZHENG X J, WANG G H . Progresses and challenges of high Reynolds number wall-bounded turbulence[J]. Advances in Mechanics,2020 ,50 (0 ):1 −49 (in Chinese). doi: 10.6052/1000-0992-19-009[18] PECORA R . Morphing wing flaps for large civil aircraft: evolution of a smart technology across the Clean Sky program[J]. Chinese Journal of Aeronautics,2021 ,34 (7 ):13 −28 . doi: 10.1016/j.cja.2020.08.004[19] HURST E, YANG Q, CHUNG Y . The effect of Reynolds number on turbulent drag reduction by streamwise travelling waves[J]. Journal of Fluid Mechanics,2014 ,759 :28 −55 . doi: 10.1017/jfm.2014.524[20] SQUIRE L C . The motion of a thin oil sheet under the steady boundary layer on a body[J]. Journal of Fluid Mechanics,1961 ,11 (2 ):161 −179 . doi: 10.1017/s0022112061000445[21] LIU T S, WANG B, WANG B, et al. Physics-based optical flow method in global flow diagnostics[C]// 27th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, Chicago, Illinois. Reston, Virginia: AIAA, 2010: 4361.
[22] 是长春 . 平板湍流摩阻系数的显式表达式[J]. 航空学报,1988 ,9 (6 ):299 −302 .SHI C C . An explicit expression of the turbulent frictional drag coefficient for a flat plate[J]. Acta Aeronautica et Astronautica Sinica,1988 ,9 (6 ):299 −302 (in Chinese).
计量
- 文章访问数: 451
- HTML全文浏览量: 13
- PDF下载量: 40
