0.   引　言

高速飞行器再入过程中，随着高度和速度降低，边界层流动会经历转捩、层流化和再次转捩的复杂过程，而转捩阵面会随雷诺数、攻角发生改变，对于轴对称飞行器，有攻角时迎风面和背风面的转捩发生位置并不相同，为非对称转捩。转捩后会引起边界层剖面特性改变，边界层厚度、摩擦阻力等改变后产生的诱导力和力矩会影响飞行器静/动稳定性^[1]，严重情况下可以显著减小阻尼动导数，导致攻角振荡、发散，对飞行安全和轨迹控制带来一定的影响。

国内外研究边界层转捩对飞行器气动特性的影响主要通过风洞实验方式进行，包括弹道靶自由飞、风洞模型自由飞、强迫和自由振动等实验。早在20世纪60年代，Ward针对半锥角10°尖锥开展了马赫数5强迫振荡实验^[2]，测量了俯仰力矩静、动导数，发现在模型下游发生转捩时尖锥静稳定性下降，动稳定性增大。Ericsson^[3-4]针对细长锥马赫数5～11风洞实验结果，进行了转捩对气动特性影响的时间准稳态分析，发现转捩处于锥体不同位置时，诱导法向力和附加气动力矩对动/静稳定性的影响有明显区别。Stetson^[5]在马赫数6风洞实验中发现带攻角的钝锥表面非对称转捩有迎风面靠前和背风面靠前两种情况，后者能够增加飞行器静稳定性，而前者降低飞行器稳定裕度甚至会导致飞行器攻角发散，并且即使在极小攻角下，非对称差异依然存在。徐国武等^[6]采用强制转捩方法对典型升力体外形开展了非对称转捩对横向静稳定性的影响研究，研究表明转捩会使飞行器航向稳定性变差，斜线非对称转捩甚至会使飞行器航向稳定性的发生改变。

国内，楼洪田^[7-10] 从80年代开始开展了边界层转捩对动稳定性影响的风洞实验研究（1985 — 2001），通过测量尖锥气动特性的转捩诱导量分析边界层转捩对静/动稳定性的影响，指出静、动稳定性转捩诱导量之间的负相关特性。高清^[11]团队、宋威^[12]团队等在风洞实验中通过纵向绊线控制边界层转捩，研究了高速飞行器非对称转捩对动稳定性、横侧向稳定性的影响，发现非对称转捩是导致高速飞行器的横侧向稳定性较差的重要原因之一，强制转捩后细长锥自由飞具有动稳定性。

国内外学者对非对称转捩影响气动力特性的原因也进行了探究，认为是转捩引起边界层厚度增大，湍流区位移厚度斜率比层流大，使得湍流区的壁面压力比层流区大，从而诱导出附加的气动力和力矩，同时转捩位置相对质心（或振心）的移动也会改变静、动稳定性。在非定常俯仰运动过程中，转捩阵面的变化对俯仰动稳定性带来影响，对于该问题，Ericsson^[3]在20世纪60年代进行了研究，根据层流/湍流边界层位移厚度斜率变化分析了转捩引起的气动力特性，认为光滑圆锥有攻角时的后体转捩会产生一个向下的诱导法向力，形成抬头力矩，使得静稳定性降低，在和姿态运动耦合后产生阻尼效应，增大动态稳定性。但这些结论是通过对气动力静/动导数随雷诺数变化特性的分析获得，缺乏直接的测量验证（受风洞实验测量技术限制），然而数值计算不仅可以获取气动力静/动导数，还可以对壁面压力和摩阻进行单独积分，分别获得压力和黏性影响量，进而对转捩影响气动特性的机制做深入研究。

尽管经过数十年研究，针对转捩影响动稳定性规律和机制方面已有初步认识，但这些认识主要来自风洞实验研究。然而，早期风洞实验测量技术手段单一，主要是测力天平和油流，缺乏对流场细节的测量，如边界层流动状态、壁面压力以及转捩阵面形状和位置，因此关于转捩影响静/动稳定性的结论和机制需要进一步的验证和研究。

数值模拟是研究流动机理和气动规律的重要手段，能够细致刻画边界层转捩前后流动变化细节，如壁面压力、摩阻分布变化，也能对压力和黏性力气动力进行单独分析，可以从多个角度研究不同流态动力/力矩和静/动稳定性的影响机制。然而在高速流动条件下，边界层转捩过程受诸多因素影响，比如来流马赫数、雷诺数、湍流度、压力梯度、流动分离、粗糙度、横流、热传导、强激波、强压缩效应等，这些因素相互作用且与当地流动参数密切相关，从而使得转捩变得异常复杂^[13]，转捩阵面形状也表现得十分复杂，目前不管是e^N方法还是RANS转捩模型依然很难对转捩阵面进行精确的模拟。但是，基于人工设置转捩位置的强制转捩方法，为转捩效应的研究提供了一个新的途径，它可以根据风洞实验测量的转捩阵面形状和位置，在计算中人为指定转捩起始点并启动湍流模型，从而实现转捩点前层流区和转捩点后湍流区的模拟。尽管该方法无法精确捕捉转捩过渡区的流动细节，但能够较好地再现风洞实验中转捩阵面的形状和位置，因此适合用来近似模拟复杂转捩形态对气动特性的影响。

本文基于高速数值模拟软件, 根据典型风洞实验结果^[14]，采用给定流向转捩位置的强制转捩方法，通过设置不同形式的动态转捩阵面，结合俯仰强迫振动数值模拟方法，计算得到非定常动态变化的转捩流场，研究了转捩阵面形状和位置对尖锥静/动态稳定性的影响，对转捩影响动态稳定性的物理机制进行了探讨，得到一些有意义的结论。

1.   数值方法

本文以高速流动模拟软件为计算平台，采用强迫振动方法进行运动和转捩过程的动态耦合仿真，通过对非定常气动力辨识获取静/动导数。数值计算采用原始变量NND二阶精度空间离散格式、 min-van混合限制器和双时间步非定常时间推进方法，湍流模型采用SST k-ω 模型，具体方法可参考文献^[15]。

1.1   边界条件

在物面上，Navier-Stokes方程要求满足速度无滑移、温度绝热或者等温以及法向的动量方程。

(1) 速度无滑移

(2) 温度条件

壁面气体温度由等温壁或绝热壁条件决定：对于等温壁T = T_wall或绝热壁$(\partial T / \partial n)=0$，n为温度沿壁面法向的梯度。

(3) 压力边界条件

要求压力满足法向动量方程（忽略黏性应力的影响）：

式中，物面加速度$\boldsymbol{a}_{\mathrm{w}}=\left(\ddot{x}_{\mathrm{w}}, \ddot{y}_{\mathrm{w}}, \ddot{z}_{\mathrm{w}}\right)，$，$n_{\mathrm{w}}$为壁面法向向量。

(4) 壁面密度

壁面气体密度由状态方程获得。

1.2   动网格技术

本文采用刚性旋转法生成动网格，将网格和物面刚性固连，网格的质量与静网格完全一致，精确地满足几何守恒定律，实现方法也较为简单，在计算过程中仅需将位置矢量乘以坐标变换矩阵即可（以俯仰运动为例） ：

其中(x₁，y₁，z₁ ) 为坐标变换前网格点坐标，(x_c，y_c，z_c )为转轴与 xOy 平面的交点，(x₂，y₂，z₂ )为旋转俯仰角θ之后的坐标。

1.3   动导数辨识

对于单自由度强迫俯仰振动，给定简谐振动：

式中：$A_{0}$为起始攻角；$A_{{\mathrm{m}}}$为振幅；$k=\omega L_{ {{\mathrm{ref}} }} / 2 V_{\infty}$为减缩频率，其中${L_{{\mathrm{ref}}}}$为参考长度，${V_\infty }$为来流速度，$\omega = 2{\text{π}} f$为圆频率，$f$为强迫俯仰振动频率。

对动态俯仰力矩系数在起始俯仰角θ处展开（保留至二阶导数），如式(5)所示：

式(5)中角度单位均为弧度，下标“0”表示在振荡中心的取值，$\left(C_m\right)_0$为振荡中心攻角处的静态俯仰力矩系数，$\left(\partial C_m / \partial \theta\right)_0$为该俯仰角的静稳定性导数，$\left(\partial C_m / \partial \dot{\theta}\right)_0$、$\left(\partial C_m / \partial \ddot{\theta}\right)_0$为动稳定性导数。本文通过积分法进行静、动导数辨识，具体可参考文献[16]。

1.4   强制转捩

地面风洞设备受喷管口径、总压参数等的因素限制，很难模拟飞行器实际飞行雷诺数，缩比实验模型的自然转捩位置通常与飞行器真实飞行的转捩位置不符。因此工程中常使用强制转捩装置（涡流发生器、粗糙带、突起物、拌线）进行转捩控制。数值模拟中转捩的实现比较简单，只需在湍流模型指定转捩位置后更新湍流黏性系数，即：

SST k-ω 两方程湍流模型^[17]是目前工程计算中广泛使用的先进湍流模型之一，本文基于该模型获得湍流黏性系数，通过式（6）进行判断来实现强制转捩模拟。

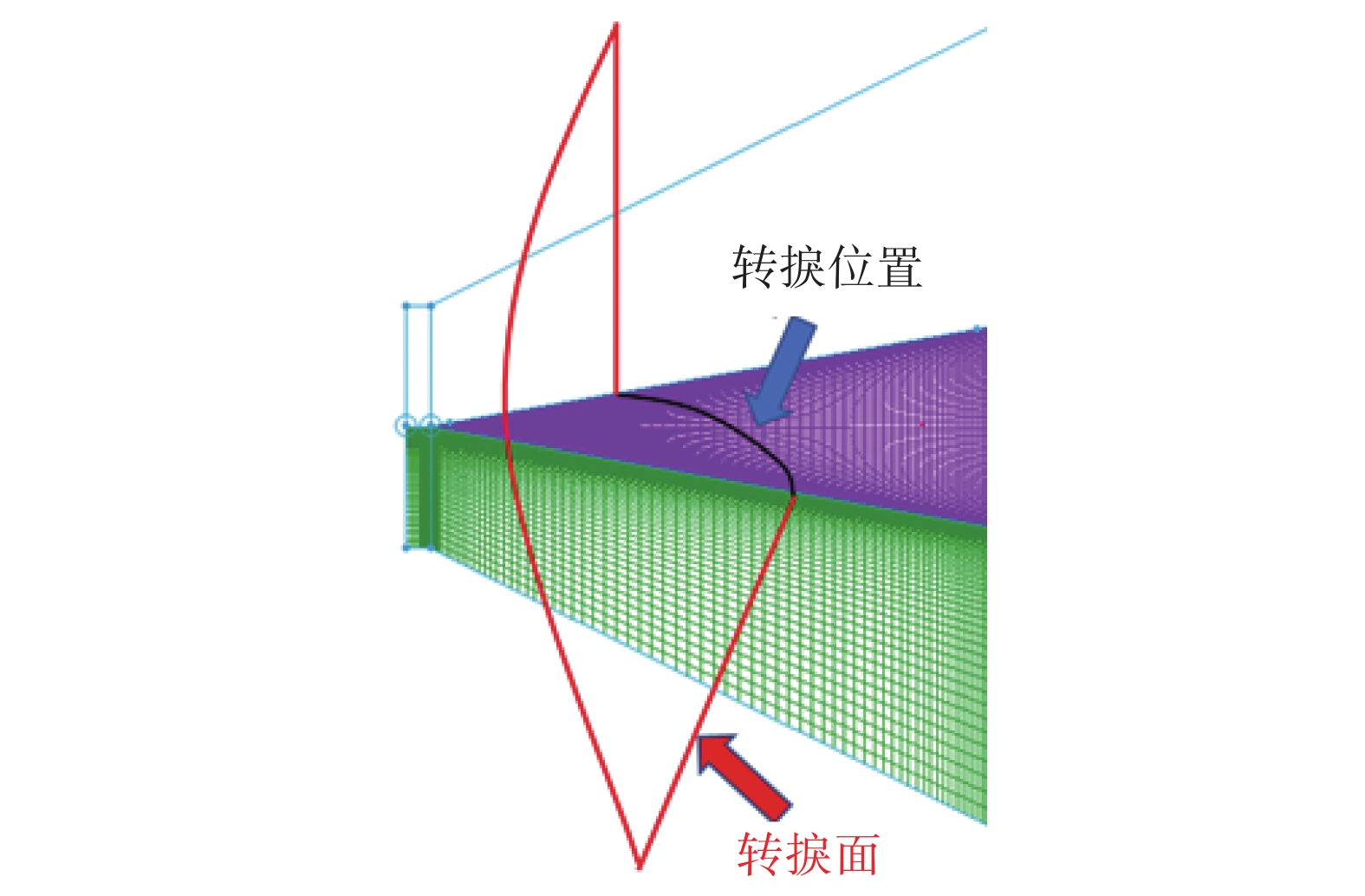
对于非对称转捩，转捩阵面在物面上所处的流向位置并不相同，而且转捩阵面形状和位置会随攻角变化而变化。对于圆锥外形，通常迎风面转捩位置靠后、背风面转捩位置靠前，从零度攻角开始，随攻角增大迎风面转捩后移、背风面转捩前移，在小攻角时圆锥表面的转捩位置如图1所示。

图  1  尖锥转捩面示意图

Figure  1.  Sketch of a cone transition front

下载: 全尺寸图片 幻灯片

计算过程中首先输入图1所示的壁面转捩位置，并在法向构建空间转捩面，将数值计算网格中的每一个网格点与构造的转捩面比较，寻找点到面的最小距离和方向，当计算网格处于转捩面上游时为层流，下游时则为湍流，使用公式（6）对湍流黏性系数进行赋值。

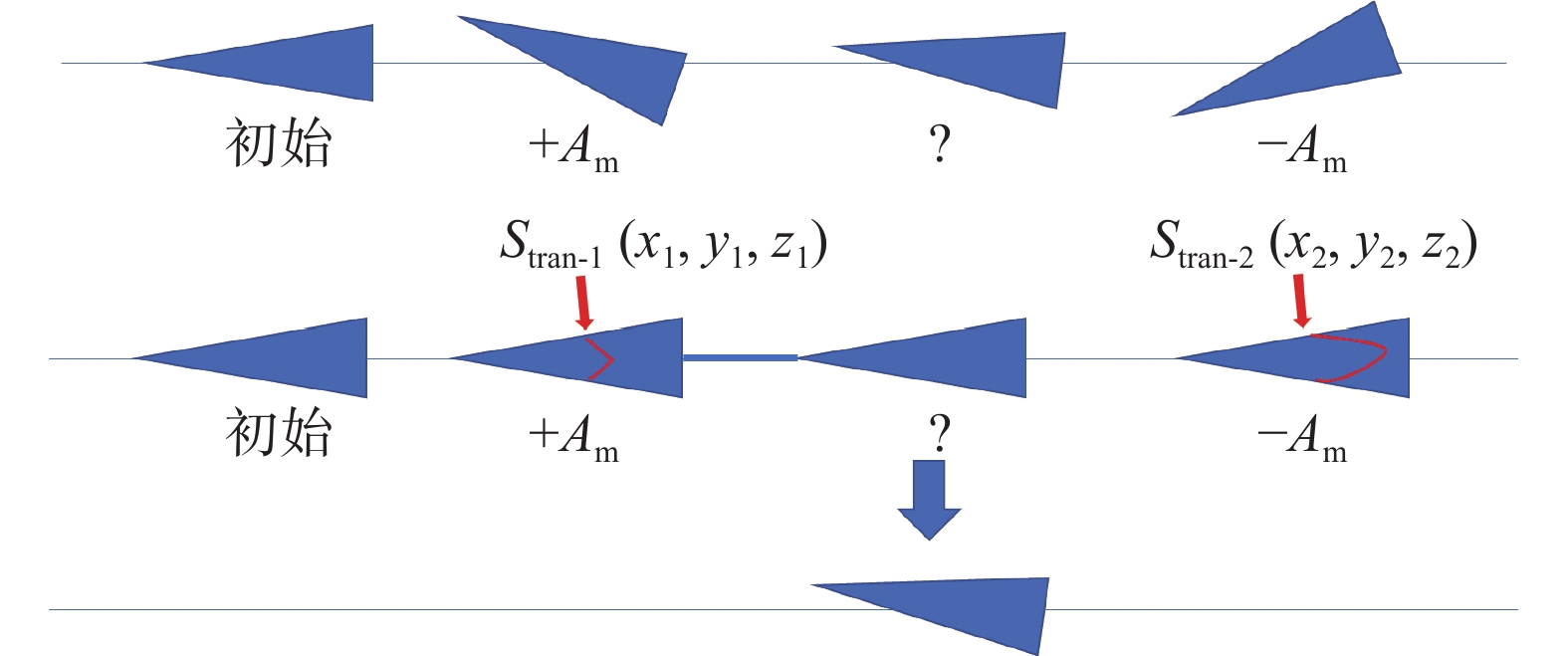
在研究飞行器动态稳定性时，一般需要进行小幅强迫振动来辨识动导数，即要求飞行器在初始平衡位置进行±A_m的刚性简谐运动，如图2所示，通常A_m取1°。由于转捩位置对攻角变化通常非常敏感，不同时刻的转捩位置不相同，因此需要在每个非定常时间步上设置转捩位置。首先设置+A_m和–A_m的转捩面（S_tran-1和S_tran-2），其他攻角的转捩位置通过线性插值获得。

图  2  俯仰强迫振动/转捩示意图

Figure  2.  Sketch of the forced oscillation/transition

下载: 全尺寸图片 幻灯片

转捩面S_tran-1和S_tran-2中任意一点的坐标分别为(x₁, y₁, z₁)和(x₂, y₂, z₂)，中间任意角度ψ∈(–A_m，+A_m)对应的转捩位置为：

随后围绕质心(x_ref, 0 , 0) z轴方向旋转，得到任意角度ψ对应的转捩面：

其中：

通过公式（8）获得任意角度ψ对应的转捩面。通过上述方法可以在强迫振动的任意时刻的转捩阵面，实现非定常强制转捩数值模拟。本文计算的外形为尖锥，因此仅考虑俯仰方向振动。

2.   算例设计与计算方法验证

楼洪田在80年代针对尖锥模型开展了边界层转捩对动稳定性影响的风洞实验研究^[8]，通过自由振动的方法测量了马赫数5、雷诺数Re_L = 2.3×10⁶～13.4×10⁶ 范围内俯仰静/动导数（L为模型长度），在测试参数范围内，随着雷诺数的增加，转捩区从底部附近逐渐向前段移动。实验中^[8]也采用了人工固定转捩方法进行了全湍流模拟，具体方法是在模型距离头部理论尖点0.2L位置安装直径0.5 mm铜丝环，其实验结果和自然转捩不同，一般认为增加人工固定转捩后，其实验结果更趋近于全湍流结果。

2.1   动导数计算方法验证

为了验证HyFLOW动态计算模块的有效性，本文选用文献[8]实验中的最大雷诺数Re_L = 13.4×10⁶流动进行模拟，该条件下尖锥流动基本处于全湍流状态，采用SST k-ω湍流模型进行全湍流状态对比计算。表1比较了HyFLOW数值计算和风洞实验测量的俯仰力矩静/动导数，数值结果与实验值偏差在15%之内。

表  1  Re_L = 13.4×10⁶条件下静、动导数结果

Table  1.  Static/Dynamic derivatives results for Re_L = 13.4×10⁶

	静导数	动导数
数值结果	–0.2031	–2.8431
实验值(人工固定转捩)[8]	–0.1770	–2.7180

下载: 导出CSV 

| 显示表格

2.2   强制转捩计算条件

采用风洞实验半锥角θ_c = 10°的圆锥模型^[8]，底部直径为70 mm，振动中心设置在X_cg = 0.652L处，来流马赫数5，总温T₀ = 373 K，来流雷诺数Re_L = 3.4×10⁶，平衡攻角α = 0°。计算网格规模为61×101×61，法向最小壁面距离为1.0×10^–5 m。动态计算时采用强迫振动，振幅取值±1°，减缩频率k = 0.015。

2.3   强制转捩阵面设计

尖锥静态转捩风洞实验结果^[14]表明，有攻角时转捩阵面呈现出非对称性，迎风区转捩靠后、背风区转捩靠前，随着雷诺数的增大，转捩阵面向上游移动。楼洪田在实验中采用油流显示技术，测量了攻角α = 0°、来流雷诺数Re_L = 3.4×10⁶时静态转捩位置，X_tr≈0.7L，但受当时测量技术限制难以清晰、准确地获取有攻角时的非对称转捩阵面位置，因此本文参考尖锥转捩阵面实验测量结果^[14]，遵循背风面转捩位置靠前、迎风面转捩位置靠后的原则，通过强制转捩方法构造尖锥攻角1°的转捩阵面。

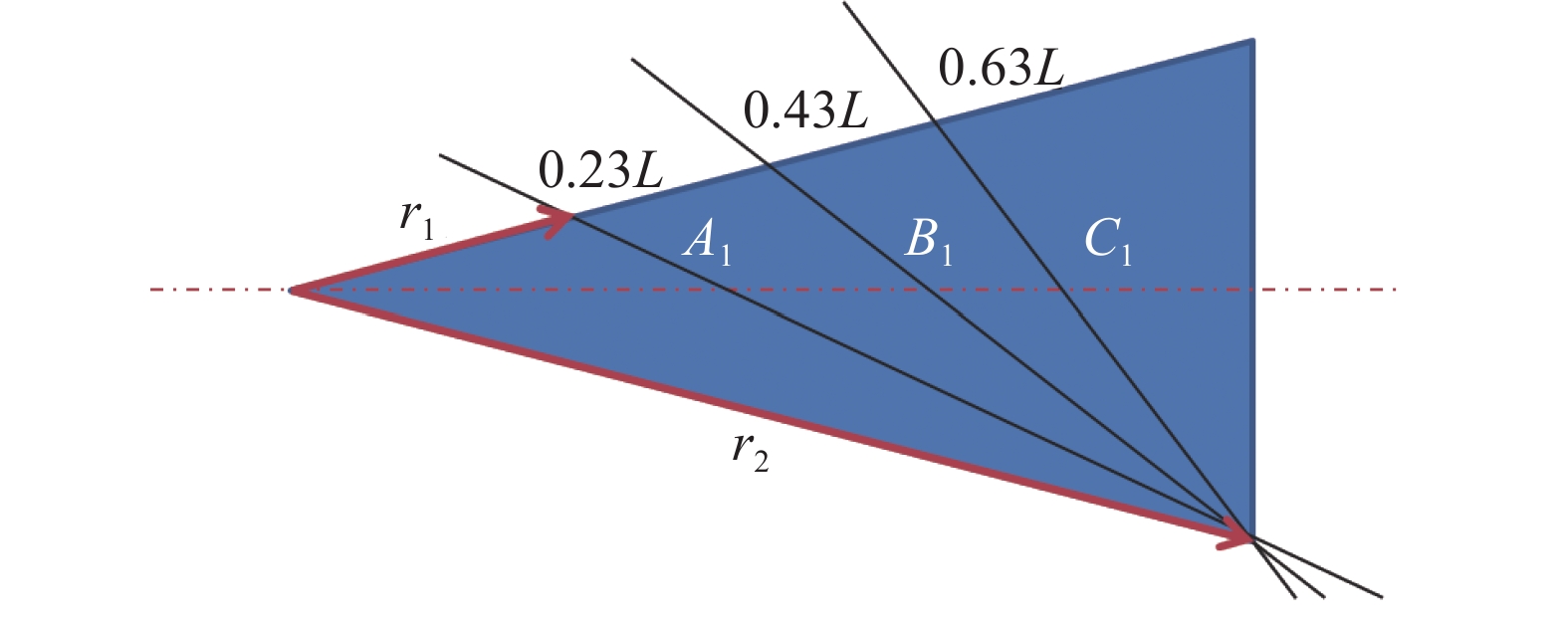
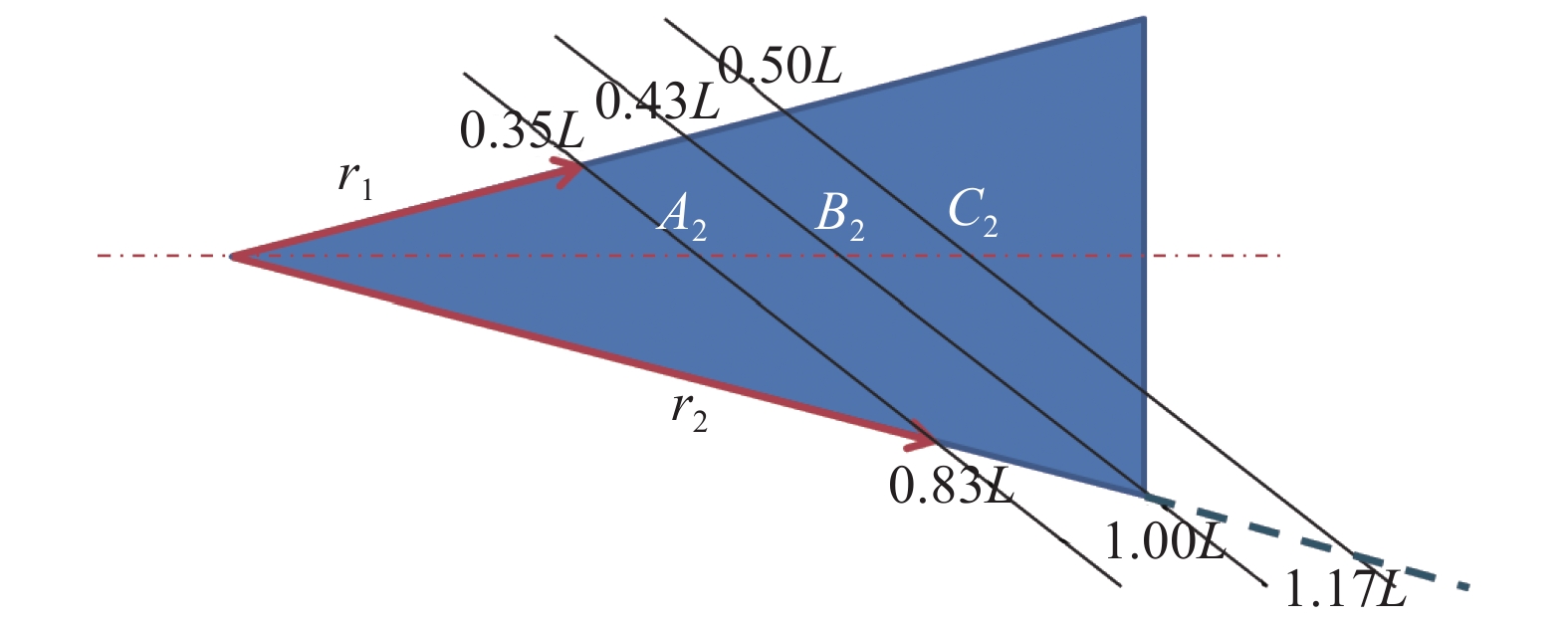
考虑到圆锥转捩位置受到来流条件、壁面条件、几何形状和外部扰动等多因素综合影响，为研究转捩阵面形状和位置变化对静动稳定性的影响，这里考虑两种形式的转捩阵面：阵面斜率变化（系列1），下缘点转捩不变，见图3；阵面位置变化（系列2），阵面斜率不变，见图4，其中转捩位置B₁和B₂相同。

图  3  系列1不同转捩阵面

Figure  3.  Series 1 of transition front shapes for a cone

下载: 全尺寸图片 幻灯片

图  4  系列2不同转捩阵面

Figure  4.  Series 2 of transition front shapes for a cone

下载: 全尺寸图片 幻灯片

转捩阵面在振幅–1°和+1°时相反，在动态计算过程中，俯仰角在±1°范围内变化，任意时刻的转捩阵面在程序内通过1.4节中的方法实现。

2.3.1   强制转捩计算方法验证

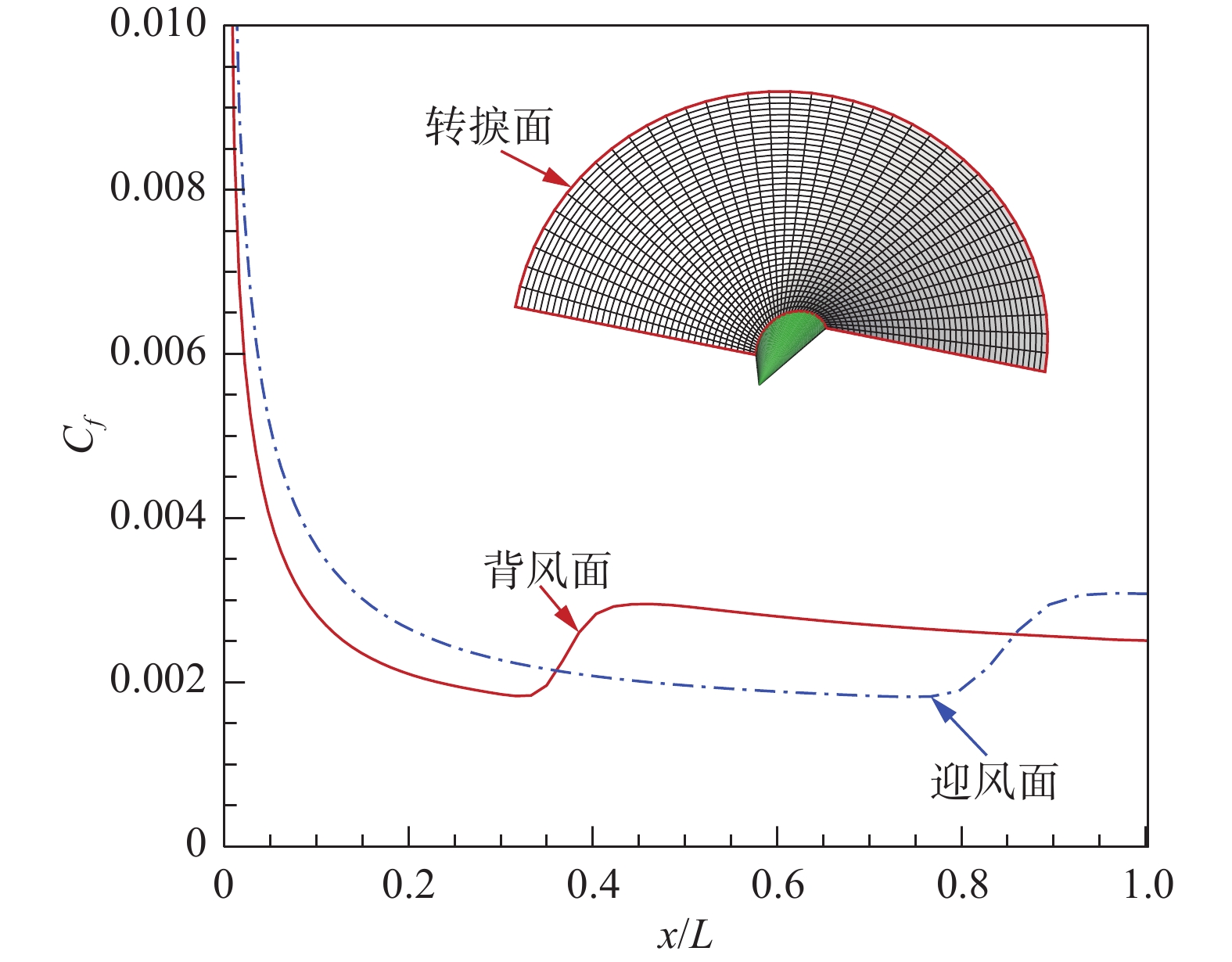
以转捩阵面A₂为例，图5给出了迎风面和背风面对称中心线上的摩阻系数，其中壁面上的转捩位置和空间的转捩面通过计算程序设置，湍流区相对层流区摩阻明显升高，流动从层流转变为湍流，转捩阵面和初始设置转捩线位置（图4）基本吻合，说明指定转捩位置的程序设置正确，实现了人工强制转捩。

图  5  转捩阵面A₂摩阻系数计算结果

Figure  5.  The skin-friction distribution of transition setup A₂

下载: 全尺寸图片 幻灯片

3.   强制转捩对静/动态稳定性的影响

参考风洞实验^[8]，根据转捩位置（阵面）随攻角、雷诺数的变化规律^[18]，通过1.4节介绍的强制转捩方式进行非定常转捩/俯仰运动数值模拟，研究转捩对圆锥稳定性的影响规律和机制。

3.1   转捩对静态气动特性影响

在研究转捩对动态气动特性影响之前，首先开展转捩对静态气动特性的影响计算，对攻角α = –1°～1°范围内的层流、强制转捩和湍流三种流态进行了数值模拟，对比分析了气动力特性。

表2给出了1°攻角时层流、湍流和转捩三种流态下气动力系数计算结果，以及转捩阵面形状和阵面变化对气动力特性的影响。全层流状态时尖锥轴向力小于全湍流状态，这是湍流黏性作用的结果，而法向力和俯仰力矩在这两种流态时几乎完全相同，说明全层流和全湍流的压力分布几乎相同。

表  2  α = 1°层流、湍流和不同转捩阵面下静态气动力系数

Table  2.  Static aerodynamic coefficients for laminar, turbulent, and transition fronts at α = 1°

流动状态	CA	CN	Cm	静导数
层流	0.0830	0.0324	–0.00355	–0.2034
湍流	0.0940	0.0324	–0.00360	–0.2064
A1	0.0899	0.0310	–0.00269	–0.1541
B1	0.0887	0.0307	–0.00214	–0.1226
C1	0.0871	0.0310	–0.00192	–0.1098
A2	0.0908	0.0317	–0.00351	–0.2013
B2	0.0887	0.0307	–0.00214	–0.1226
C2	0.0869	0.0308	–0.00168	–0.0960

下载: 导出CSV 

| 显示表格

转捩发生时轴向力介于全层流和全湍流之间，但法向力和俯仰力矩都相对减小。整体来看，改变转捩阵面斜率（系列1）和阵面位置（系列2）的两种强制转捩阵面形式对气动力影响规律相似。转捩阵面斜率变化对轴向力和法向力的影响较小，最大不超过6%，但对俯仰力矩的影响较大，随着转捩的后移（A→B→C），俯仰力矩系数明显减小，其中A₂到B₂的过程中俯仰力矩变化最大，约为45%，静导数也随转捩阵面位置后移而减小约45%。所有转捩状态下俯仰力矩静导数小于层/湍流状态，说明转捩使尖锥俯仰静稳定性降低。

3.2   转捩对动态气动特性影响

与静态转捩计算相同，选择雷诺数Re_L = 3.4×10⁶的计算条件，对尖锥开展了不同流动状态、转捩阵面的数值模拟，分析了转捩对俯仰动导数的影响规律。

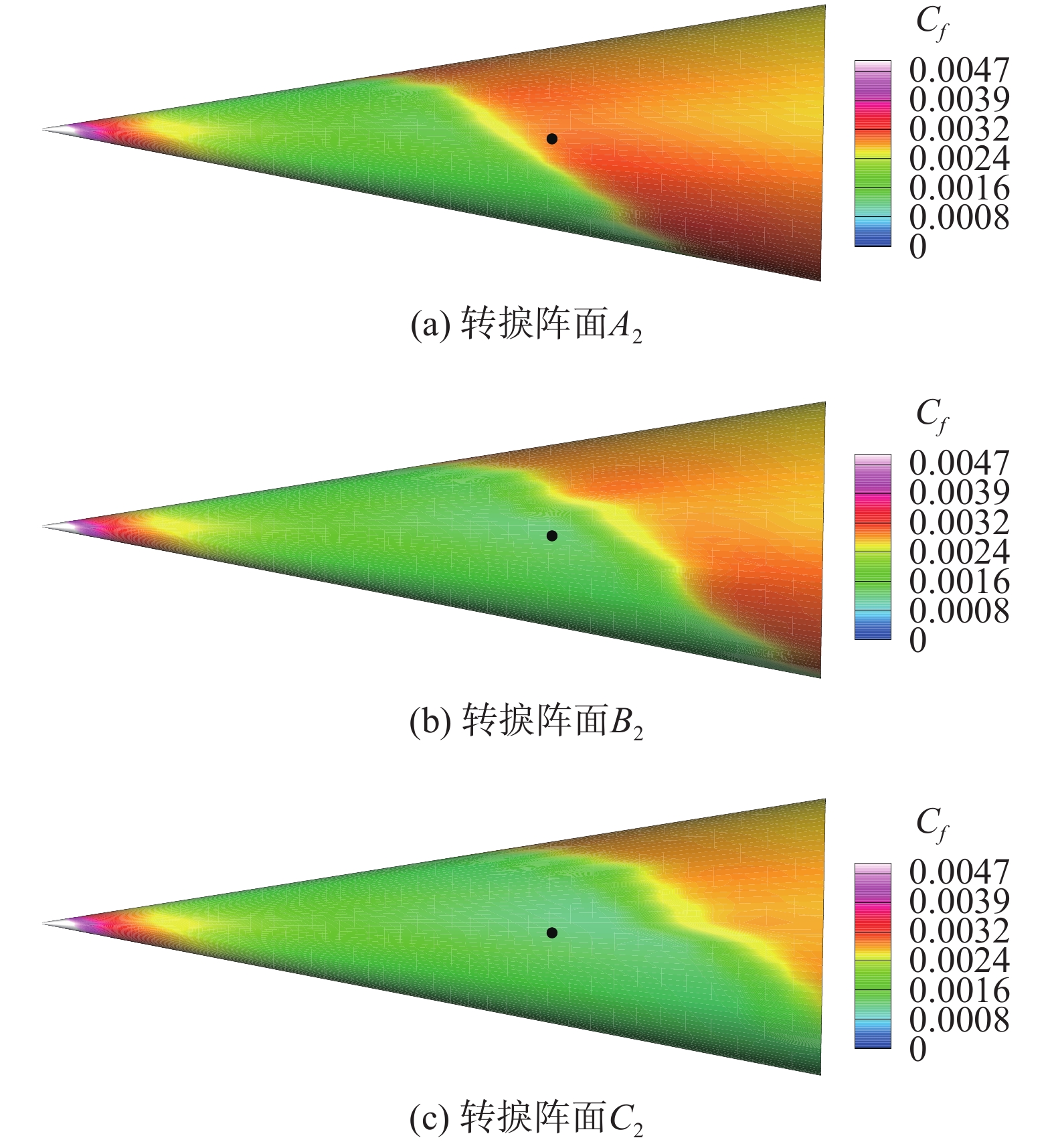
图6给出了系列2转捩阵面在流向位置平移时的表面摩阻分布变化，可以看到A、B、C 3种条件下的转捩阵面依次向下游变化，再次验证了1.4节构造的强制转捩模拟方法。由于数值模拟采用离散网格的原因，转捩阵面在局部位置出现锯齿状，但仍可以描述其转捩阵面形态的变化。

图  6  转捩阵面系列2振幅+1°时摩阻分布

Figure  6.  Distribution of skin-friction with amplitude of +1° for transition series 2

下载: 全尺寸图片 幻灯片

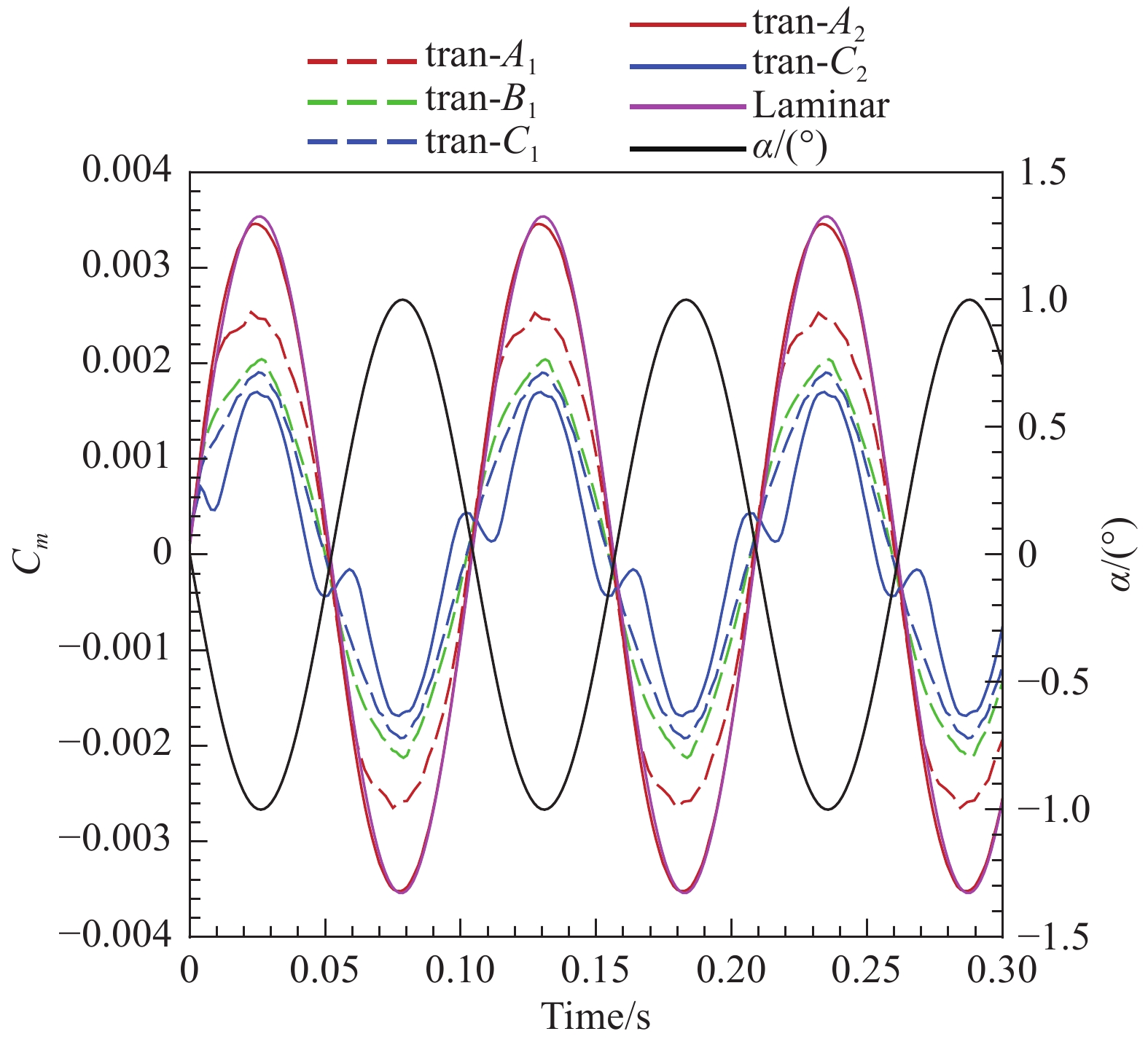
图7为不同转捩阵面时俯仰力矩随时间变化历程曲线（定义抬头力矩为正）。从图7中可知俯仰力矩曲线基本呈现正弦曲线的变化规律，与攻角随时间变化曲线相似。系列1（A→B→C）幅值逐步减小，系列2（A→B→C）幅值变化更大，规律和静态气动力相似。与层流的俯仰力矩相比，随转捩阵面后移，C_m曲线越来越偏离层流状态，A₂幅值最大，最接近层流状态，说明其转捩诱导力矩最小；C₂幅值最小，说明转捩效应最强。另外，C₂时间历程曲线与其他转捩方式有明显不同，C_m在0°攻角附近出现小幅振荡，主要原因是C₂转捩位置最靠下游，其非对称力积分面积的变化量与其他转捩形式有所不同，在攻角接近±1°时转捩阵面超出尖锥表面，此时转捩效应最强，而当攻角幅值减小接近平衡态时转捩阵面才完全作用在尖锥上，此时非对称转捩效应又很弱，其C_m曲线在平衡攻角附近不像其他转捩形式那样呈单调变化，而是呈现小幅振荡。

图  7  不同转捩阵面俯仰力矩系数时间历程曲线

Figure  7.  Time history curves of pitch moment coefficients for transition fronts

下载: 全尺寸图片 幻灯片

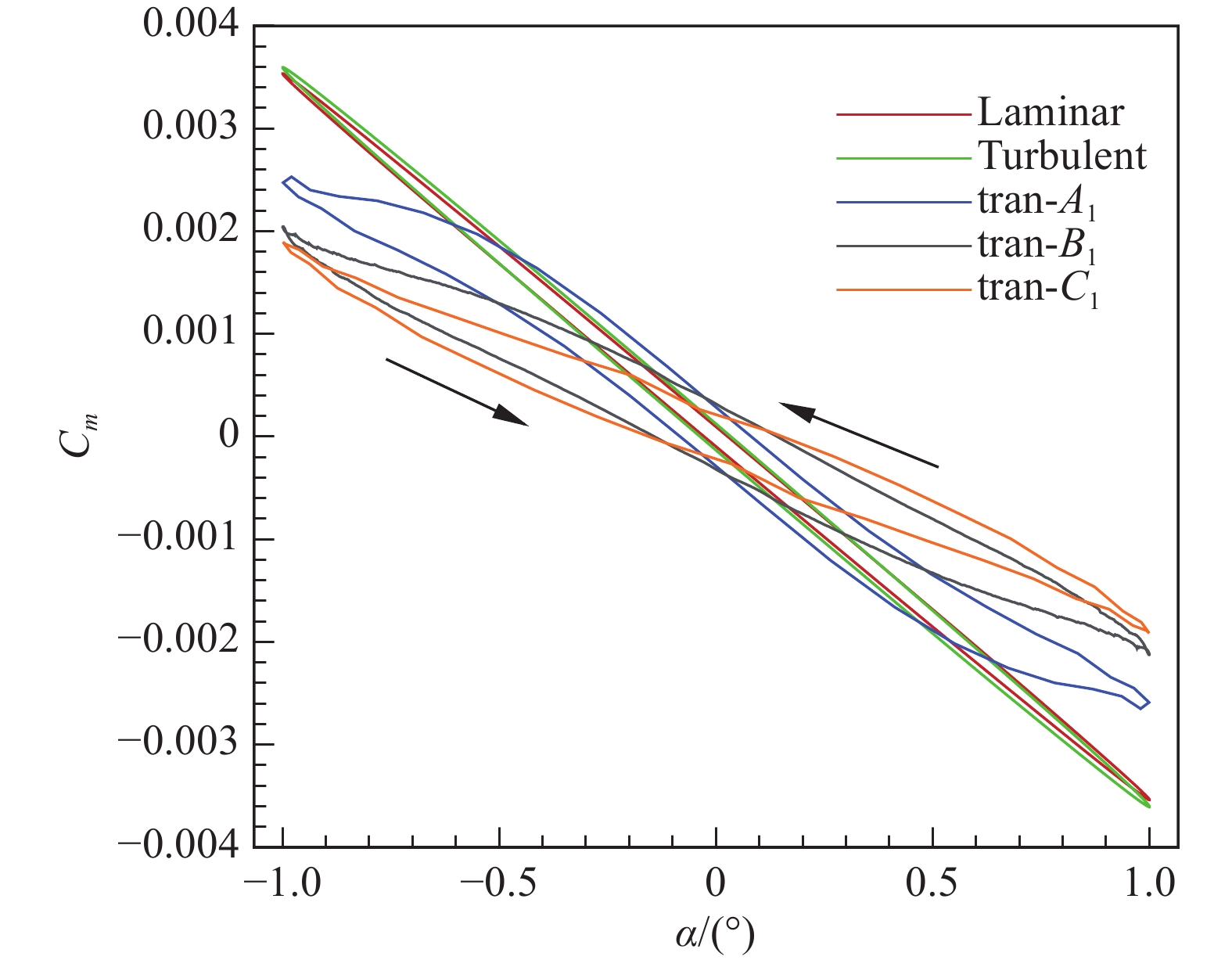
图8给出了转捩阵面系列1俯仰力矩迟滞环，从图中可知，全层流和全湍流迟滞环的大小和斜率十分接近，并且是稳定的。有转捩发生后迟滞环形状发生明显改变，迟滞环包围面积增大，但方向未发生改变，说明动稳定性增大。迟滞环斜率随转捩阵面后移逐渐偏离层/湍流状态，按照A→B→C的顺序逐渐减小，对应了表3中静导数的减小。

图  8  系列1俯仰力矩系数迟滞环

Figure  8.  Pitch moment coefficients hysteresis loop of series 1

下载: 全尺寸图片 幻灯片

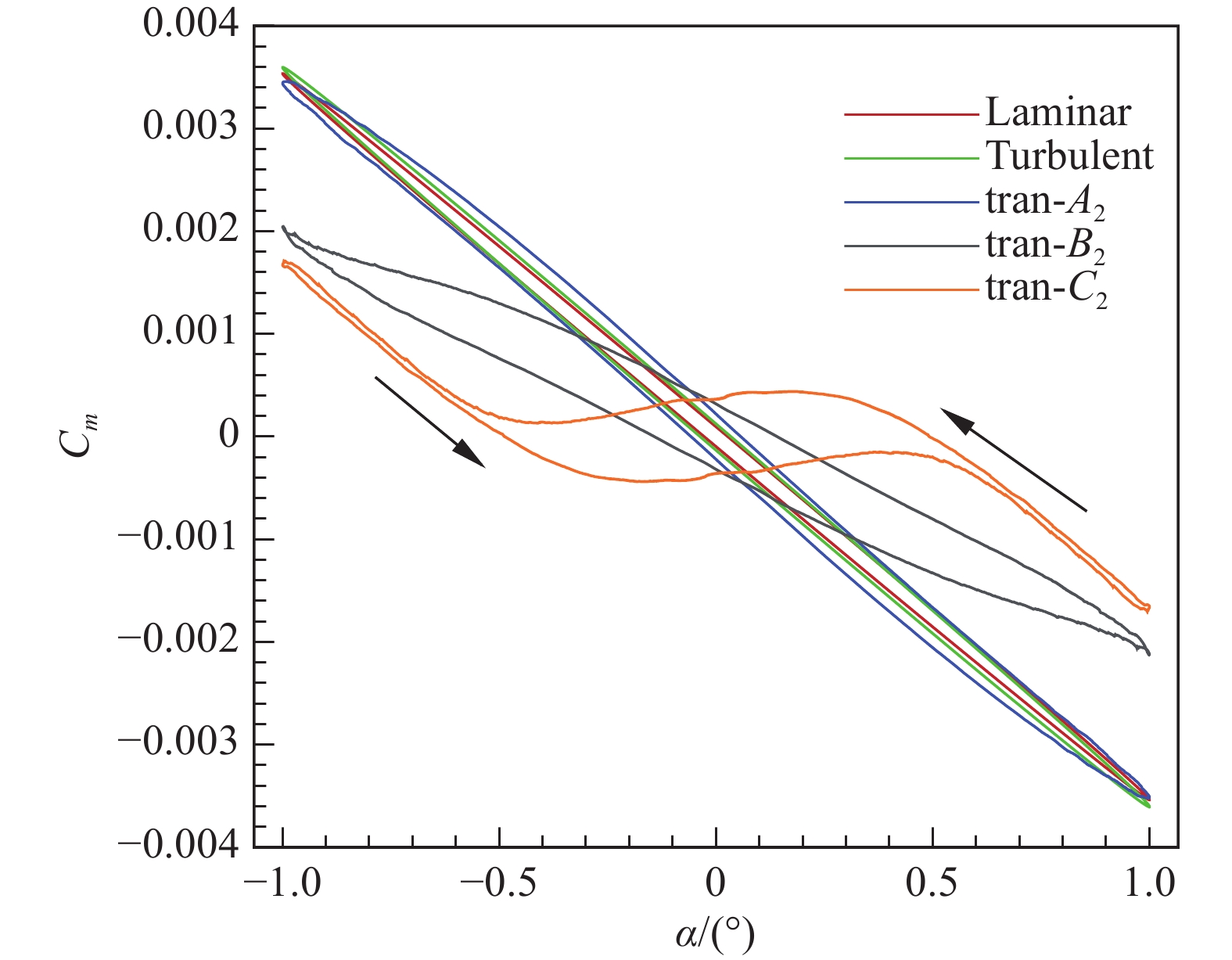
表  3  不同状态下的俯仰力矩静、动导数

Table  3.  Static and dynamic derivatives of different cases

流动状态	静导数	动导数
层流	–0.2027	–2.2099
湍流	–0.2060	–2.3043
A1	–0.1556	–6.4420
B1	–0.1156	–6.3334
C1	–0.1027	–4.9334
A2	–0.2033	–4.8612
B2	–0.1156	–6.3334
C2	–0.0755	–4.4857
实验值[8]	–0.0437	–3.9830

下载: 导出CSV 

| 显示表格

图9给出了转捩阵面系列2俯仰力矩迟滞环，相较于系列1，系列2转捩阵面迟滞环斜率和形状变化更大。A₂和全层流、全湍流时迟滞环相似，表明A₂阵面上下表面非对称转捩引起的气动力对俯仰力矩的影响较小；随着转捩阵面逐步后移到B₂时迟滞环面积和斜率发生明显变化；当转捩阵面进一步后移到C₂时，迟滞环形状明显改变，在平衡攻角附近静导数符号改变，这是由C₂转捩阵面特殊性造成，图7俯仰力矩系数时间历程曲线中已有解释。

图  9  系列2俯仰力矩系数迟滞环

Figure  9.  Pitch moment coefficients hysteresis loop of series 2

下载: 全尺寸图片 幻灯片

通过对非定常数值模拟获得的俯仰力矩系数进行辨识，可以获得俯仰力矩静、动导数，见表3。从表中可知，全层流和全湍流状态时静导数差异很小，和表1中静态计算的静导数几乎一致，转捩状态下静导数和静态时也比较接近，多数情况下相差小于约10%。与静态模拟结果相似，随着转捩阵面的后移，俯仰力矩静导数逐渐减小，其中C₂阵面的静导数约为A₂阵面情况的1/3。几乎所有转捩状态下辨识的俯仰力矩静导数绝对值都小于全层流/湍流，即转捩降低了静稳定性，这与静态规律相同。

表3中也给出了非定常流动辨识的俯仰力矩动导数。可以看到，全层流和全湍流时动导数十分接近，而所有转捩情况下动导数绝对值明显增大，约是层/湍流的2～3倍，由于动导数都为负值，说明是动稳定性增强。系列1转捩阵面向下游移动时，动导数在负向逐渐减小，转捩诱导的动稳定增强效应减弱。系列2转捩阵面向下游平行移动时，动导数绝对值先增大后减小，B₂的动稳定性最强。其中C₂转捩阵面静/动导数和风洞实验测量结果最为接近，间接说明C₂转捩阵面形式可能最符合风洞实验情况。

3.3   转捩影响气动特性的机理分析

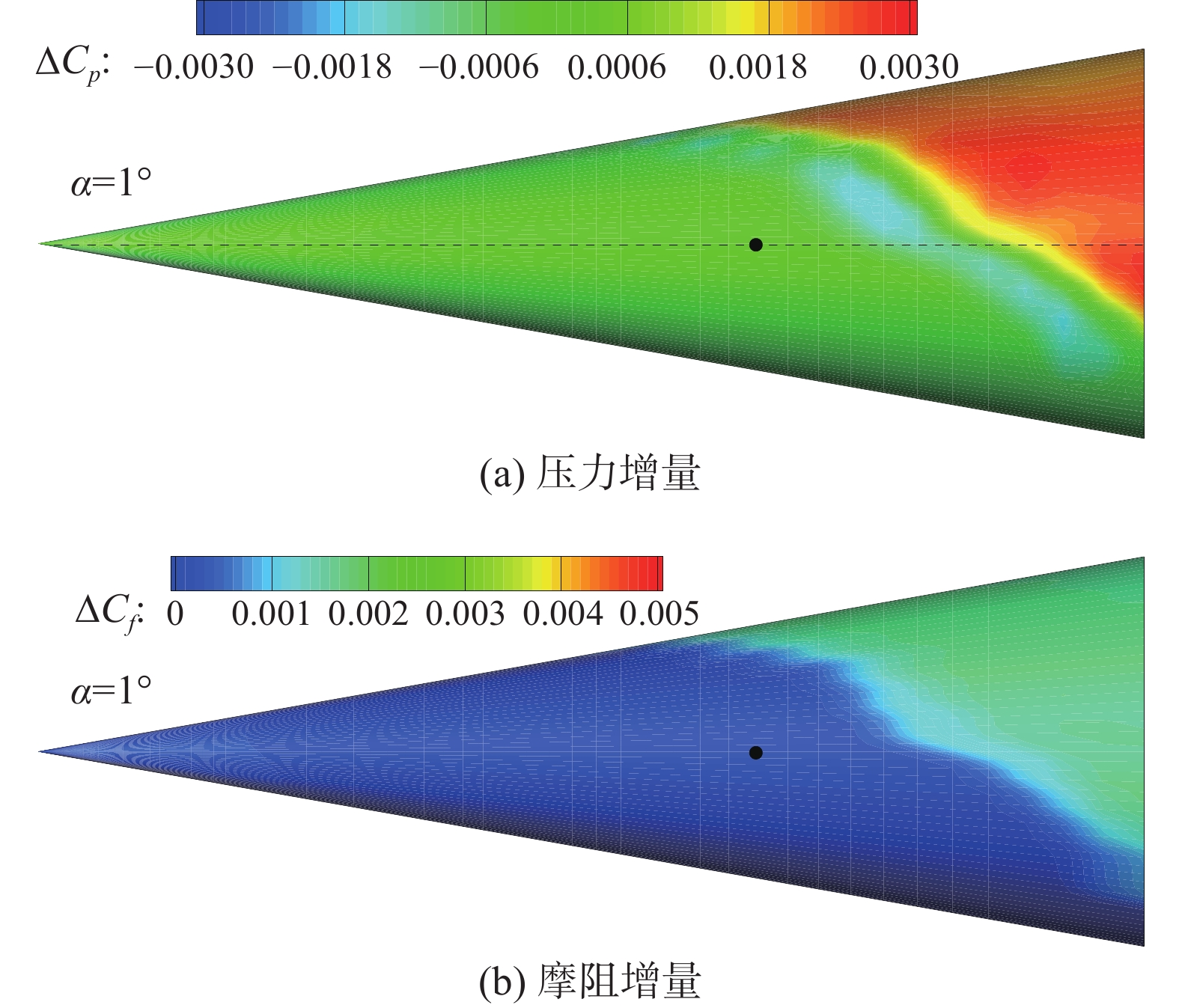
下面以C₂转捩为例，对转捩影响尖锥静/动稳定性的原因作进一步分析。首先将静态转捩流场和静态层流流场进行差量计算，得到转捩引起的壁面压力和摩阻变化，见图10。可以看到，边界层转捩后在湍流区的壁面压力增大，由于转捩起始位置在圆锥周向是有变化的，即非对称转捩，压力增量在周向随转捩位置而变化，沿转捩阵面呈不对称分布。当α = 1°时，上表面转捩比下表面靠前，上表面的压力增高区域大于下表面，因此诱导产生一个向下的法向力，由于转捩区域在质心下游，因此该诱导力会产生一个附加的抬头力矩。而边界层转捩后壁面摩阻也会增大，与压力增量分布类似，上、下表面的摩阻增量也是非对称的，而且上表面的增量区域大于下表面，显然该阻力产生的力矩也会引起附加的抬头力矩（见表4）。

图  10  转捩引起壁面压力和摩阻增量

Figure  10.  Increment of pressure and skin-friction induced by transition

下载: 全尺寸图片 幻灯片

表  4  攻角1°时不同转捩阵面下俯仰力矩系数增量

Table  4.  Pitch moment coefficients increment of the transition fronts at α = 1°

状态	ΔCm	ΔCm, p	ΔCm, f
A2	0.00003	–0.00024	0.00027
B2	0.00141	0.00096	0.00045
C2	0.00187	0.00136	0.00051

下载: 导出CSV 

| 显示表格

表4给出了攻角1°时3种不同转捩阵面情况下的附加俯仰力矩。3种情况下，总附加力矩都为抬头力矩（符号为正），且随着转捩位置向下游移动（A→B→C）附加力矩增大。进行有黏和无黏分解后得到力矩分量（ΔC_{m, f} 、ΔC_{m, p}），分别对应摩阻和压力产生的附加力矩。可以看到，压力分量是总力矩的主要贡献，转捩位置后移，压力产生的附加力矩增长快于摩阻力矩。由此可知，圆锥表面压力变化是转捩非对称力矩的主要来源。

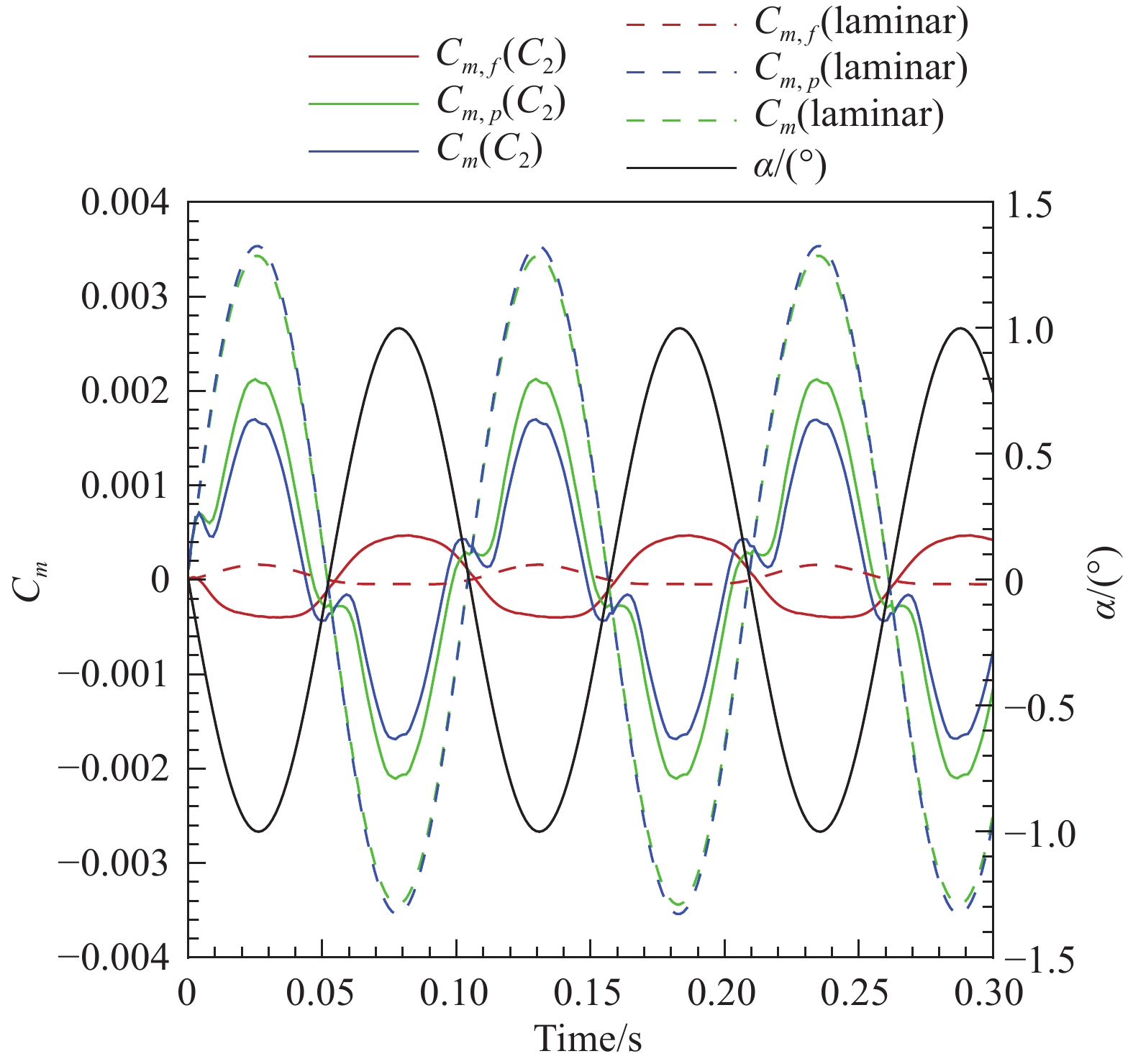
在俯仰运动过程中，尖锥俯仰力矩随时间（攻角）呈周期振荡变化，在非定常气动力/力矩计算中可以将非定常气动力分解为有黏（摩阻）和无黏（压力）两部分。图11给出了层流和C₂转捩两种工况下俯仰力矩各分量时间历程。在层流状态下，总俯仰力矩和压力分量力矩几乎完全重合（除了在α = ±1°附近很小区域外），摩阻力矩分量很小，但其随攻角变化趋势和压力分量一致。在C₂转捩状态下，无黏压力分量（C_{m, p}）的力矩曲线和总力矩（C_m）曲线的形状接近，但C_{m, p}绝对值略高于C_m，摩阻分量（C_{m, f}）力矩较小，其变化趋势和压力分量的变化趋势相反，造成总的俯仰力矩在多数攻角区间略小于压力分量力矩。

图  11  俯仰力矩系数时间历程曲线

Figure  11.  Time history curves of pitch moment coefficients

下载: 全尺寸图片 幻灯片

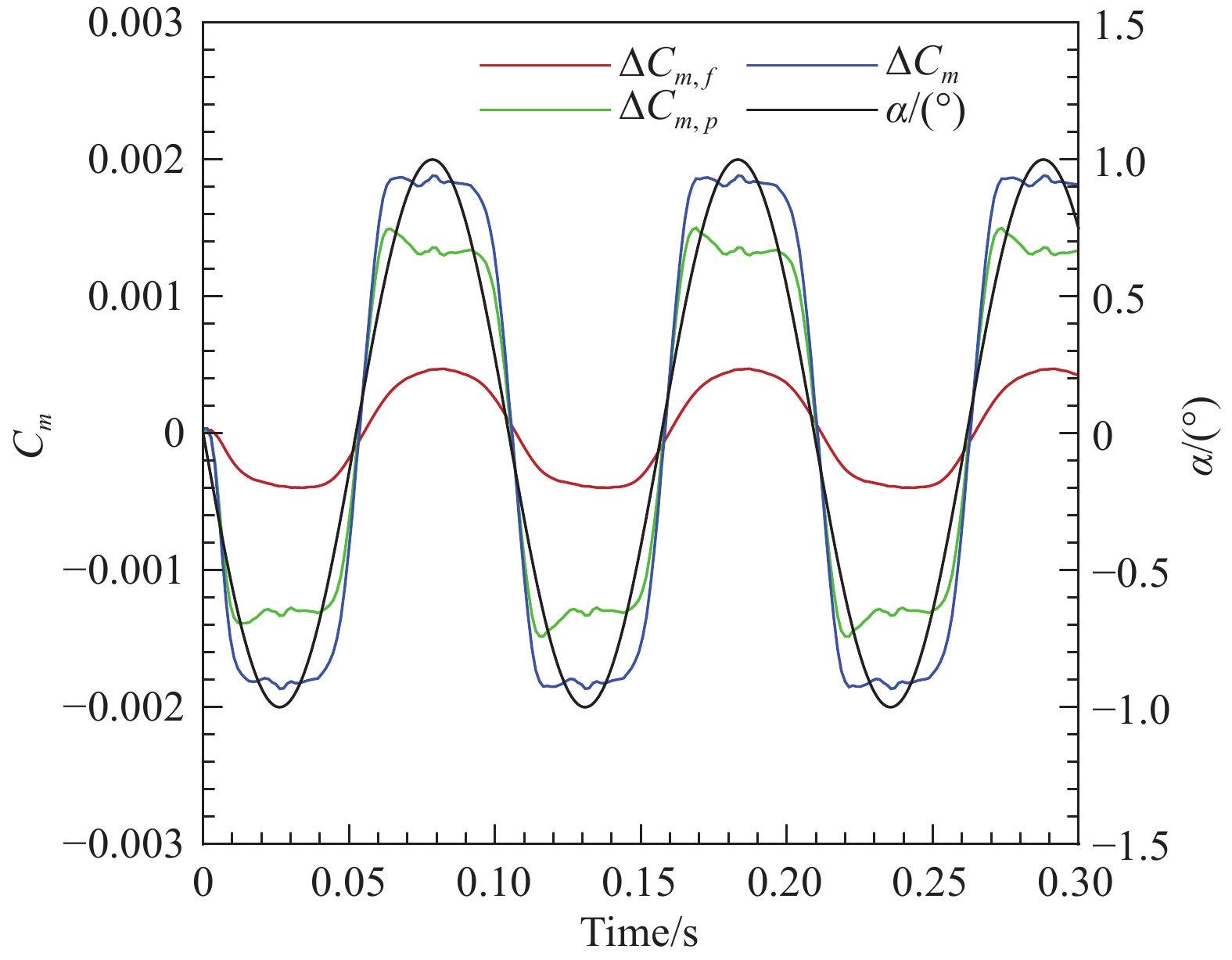
图12给出了俯仰力矩各分量的转捩诱导增量随时间变化历程，摩阻和压力分量随攻角变化趋势相同，正攻角时产生抬头力矩，负攻角时反之，这和静态计算的结果类似，压力分量大于摩阻分量，是构成转捩附加力矩的主要成分。与图11相比，也可以看到，转捩引起的力矩增量随时间变化方向与整体力矩相反，即起到减小力矩大小的作用，和前面分析的静稳定性降低特性一致。

图  12  转捩阵面C₂俯仰力矩系数增量时间历程曲线

Figure  12.  Time history curves of pitch moment coefficients increment for transition front C₂

下载: 全尺寸图片 幻灯片

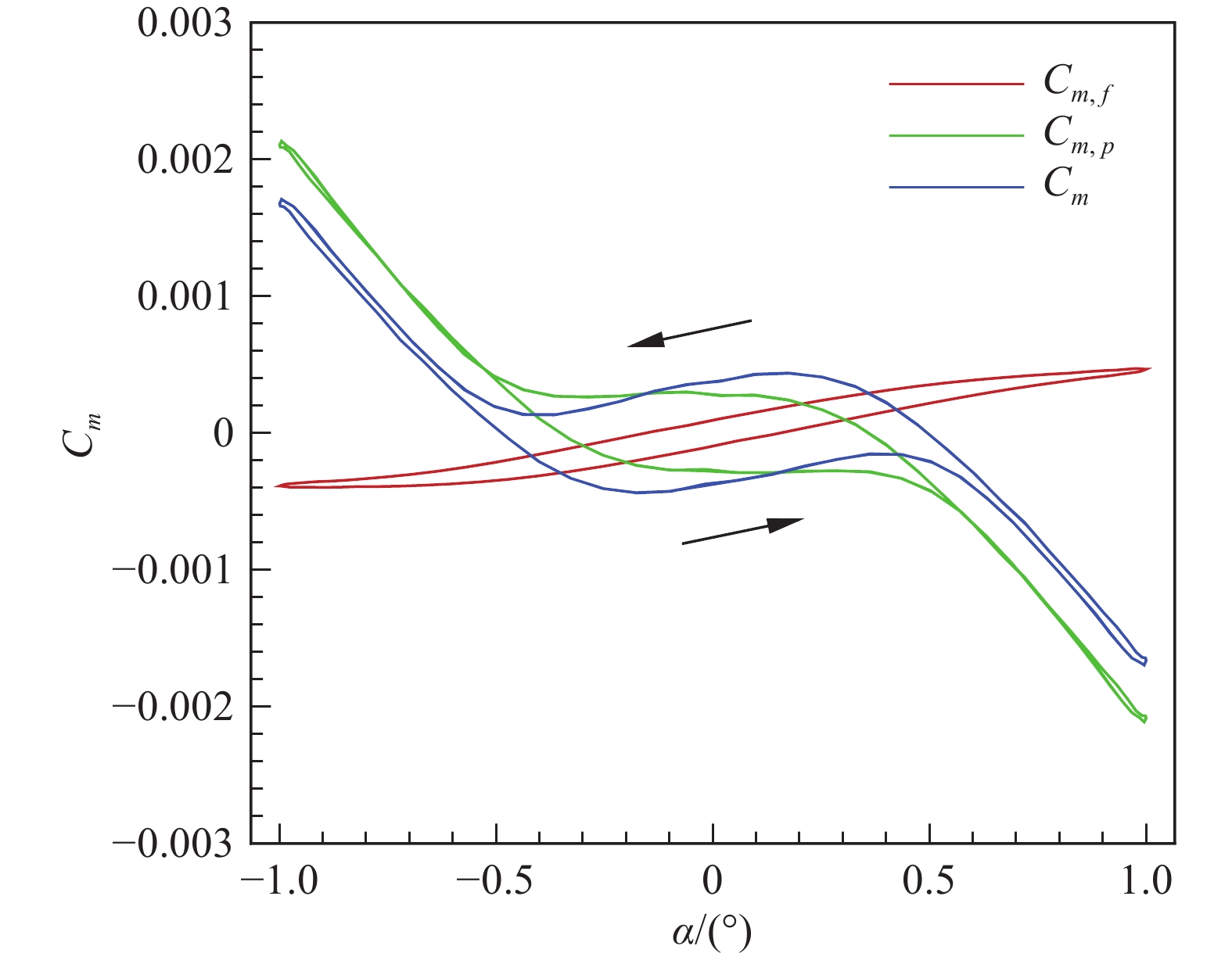
图13给出了俯仰力矩各分量迟滞环，3种分量迟滞环方向相同，动导数为负，无黏分量迟滞环形状和整体量的相似，但与黏性分量相差较大。两种分量迟滞环两端顶点斜率相反，即C_{m, f}对应的静导数为正，C_{m, p}的为负，但整体静导数分量中C_{m, p}起绝对主导作用。表5给出了图13中迟滞环辨识后的静/动导数，整体动导数中无黏分量占比较大，约62%，进一步验证了之前的结论，转捩引起的压力变化在对静/动稳定性影响中起主导作用。

图  13  转捩阵面C₂俯仰力矩系数迟滞环

Figure  13.  Pitch moment coefficients hysteresis loop of transition front C₂

下载: 全尺寸图片 幻灯片

表  5  摩阻和压力分量的静、动导数

Table  5.  Static and dynamic derivatives of the skin-friction and pressure

状态	静导数	动导数
摩阻分量	0.0267	–1.6939
压力分量	–0.1021	–2.7918（62%）
总和	–0.0755	–4.4857

下载: 导出CSV 

| 显示表格

4.   结　论

本文基于高速数值模拟软件开展了尖锥强制转捩对静/动导数影响的研究。通过设置不同形式转捩阵面对尖锥模型进行了静态和动态数值模拟，获得了气动力/力矩随转捩阵面变化规律，分析了转捩对俯仰静/动稳定性影响机制，得到以下结论：

（1） 转捩阵面变化会影响静态气动力，随着转捩阵面的后移，俯仰力矩减小，相比全层流/全湍流状态静稳定性降低；转捩阵面变化对动导数影响明显，转捩后的俯仰动稳定性相比层流和湍流状态显著增强，动导数增大约1～2倍。

（2） 两种转捩形式对尖锥俯仰静/动稳定性的影响规律相似，都会降低静稳定性，增加动稳定性，其中C₂转捩计算的静/动导数和风洞实验值符合度最好，推测该转捩形式可能最为接近风洞实际情况。

（3） 边界层转捩后诱导出压力和摩阻增量，产生的附加俯仰力矩与整体力矩方向相反，而且在俯仰力矩动导数中压力分量起主导作用，说明转捩后引起的压力变化是导致动态效应影响的主要因素。

（4） 本文构造的动态转捩的模拟方法可以实现快速有效的动态转捩数值预测，鉴于动态转捩风洞实验相比静态风洞实验难度大、周期长，尤其缺乏对流场细节的测量，本方法可以将静态风洞转捩实验结果做为输入，开展相关的转捩动态过程模拟。