Numerical simulation of hypersonic magnetofluid control based on non-linear coupling constitutive relation
-
摘要:
针对高速等离子体在磁场中的复杂非线性流动问题，由于连续介质理论的N-S方程已不再适用，本文通过耦合非线性耦合本构方程和Maxwell电磁场控制方程，结合Park TTv双温度模型和Park11组分化学反应模型，建立了低磁雷诺数高速磁流体热化学非平衡数值模拟方法。基于高速等离子体圆柱扰流算例的数值模拟，研究了偶极子磁场对高速磁流体控制的影响机理，重点分析了磁场的存在以及磁感应强度的大小对等离子体流场结构的影响。研究结果表明：磁场将会显著影响高速等离子体流场结构，磁感应强度增大，带电粒子所受洛伦兹力增强，导致弓形激波脱体距离增大，当B0 = 3T时，激波脱体距离增幅达452.38%；驻点热流变化受磁感应强度、来流高度、来流马赫数共同影响，当H = 80 km时，加入磁场后热流降幅达45.55%；此外，磁场对高速磁流体热化学非平衡效应影响较为显著，主要体现在波后N2的离解程度和近壁面的复合反应等方面，而对O2的离解过程影响不大。
Abstract:To address the complex nonlinear flow mechanisms of high-speed plasma in magnetic fields, the conventional Navier-Stokes (N-S) equations based on continuum theory fail to provide accurate predictions. Therefore, A novel framework was developed by coupling the Nonlinear Coupling Constitutive Relations (NCCR) with Maxwell's electromagnetic field governing equations, augmented with the Park's TTv two-temperature model and the Park 11-component chemical reaction model. This integration established a numerical simulation method and code for hypersonic magnetohydrodynamic (MHD) thermochemical non-equilibrium under low magnetic Reynolds numbers conditions. Numerical simulations of high-speed plasma flow past a spherical body were conducted to investigate the influence mechanism of a dipole magnetic field on high-speed MHD control, with particular focus on the effects of magnetic field existence and its induction strength on plasma flow field structures. The results show that the presence of a magnetic field significantly alters high-speed plasma flow structures, with stronger magnetic fields inducing greater Lorentz forces on charged particles and consequently increasing bow shock detachment distances (e.g., a 452.38% increment observed at B0 = 3 T). Stagnation point heat flux variations exhibit dependence on multiple factors including magnetic induction strength, inflow altitude, and Mach number, showing a notable 45.55% reduction at H = 80 km after magnetic field introduction. Furthermore, the magnetic field induces prominent thermochemical non-equilibrium effects, primarily enhancing N2 dissociation in post-shock regions while modifying recombination reactions near walls, yet exerting minimal influence on O2 dissociation dynamics.
-
0. 引 言
飞行器高速飞行时，飞行器前缘脱体弓形激波导致流场温度与压力急剧升高，气体粒子热运动加剧，振动能被激发。温度升高到一定程度时，将会发生剧烈的物理化学反应，多组分气体发生离解、电离、复合、交换等反应，气体分子内能模态不同程度被激发，形成具有弱导电性的等离子体流场[1]。当高温气体与壁面接触后，由于温差较大将会产生巨大的热流。为了降低飞行器表面热流，对飞行器实施更好的热防护，磁控热防护技术在20世纪50年代被提出。起初磁控热防护并不具有现实意义，若要达到降低气动热的效果，需建立巨大且笨重的磁体结构。然而磁流体控制技术经过50多年的发展，具有超导性质的磁体系统不断进步，目前已构建重量约380 kg、中心磁场约1.2 T（线圈直径0.9 m，线圈长度1.4 m）的薄型超导螺线管磁体系统[2]。磁体系统的不断发展使得磁流体控制技术在再入返回舱等高速飞行器热防护应用中逐渐得以实现。
在磁流体控制技术发展过程中，数值模拟技术相较于实验研究而言，起步较晚，但所需的人力、物力成本显著降低，通过数值模拟可以得到流场结构信息，有助于研究人员直观地了解流场规律。磁流体控制数值模拟技术经过近几十年的发展，尤其是近些年不断地对计算格式进行修正，其准确性不断提高，发挥着越来越重要的作用[3]。胡宁等[4]通过数值模拟研究了正交电磁场控制装置中外加电场强度、磁场强度等参数对等离子体电子密度控制效果的影响规律。相比于传统的计算流体力学（Computational Fluid Dynamics, CFD）数值模拟，高速磁流体控制数值模拟涉及多种复杂物理现象，包括产生和维持带电粒子的过程、带电粒子与磁场的作用、电磁场中的霍尔效应等[5]。
在高速磁流体控制数值模拟研究方面，国内外开展了系列研究。例如早期的Hoffmann等[6]模拟了半球体高速绕流流场，旨在研究电磁干扰效应对钝体绕流流场的影响。1988年，Brio与Wu[7]应用Roe格式求解了一维的磁流体动力学（Magnetohydrodynamics, MHD）激波管问题，准确捕捉到了复杂的磁流体动力学波系结构。日本的Fujino[2]团队数值研究表明，基于OREX飞行工况的低轨道条件下（60 km），施加0.5 T磁场可使对流热流降低20%，且随高度增加效果更显著。Alexis Lefevre等[8]通过耦合欧拉方程与Maxwell电磁场方程，研究了磁流体流动控制对行星返回舱周围电离冲击层的影响，为未来的MHD气动制动实验提供了框架，同时说明了磁控热防护的可行性。国内丁明松等[9]采用三维低磁雷诺数磁流体动力学数值模拟方法及程序，分析了电导率模型对高速磁流体流场分布、气动力/热特性的影响。罗凯等[10]通过数值模拟方法研究了不同磁感应强度、磁体位置对双锥模型绕流流动结构及流场内关键参数分布的影响机理和规律。徐帅等[11]建立了多组分双温度模型的非平衡气体控制方程，给出了相关输运系数和化学反应参数的计算方法。总结来看，虽然目前的研究涵盖了多方面的影响，比如热化学反应、霍尔效应以及电导率模型等因素的影响，但是高空高速飞行引起的热化学非平衡效应、稀薄气体效应尚未被完全考虑，同时N-S方程在稀薄流域将不再满足连续性假设，气体流动的非线性现象逐渐凸显[12]。
目前针对高空稀薄流动，非线性耦合本构（nonlinear coupling constitutive relations，NCCR）方程不仅在连续流域能够回归N-S方程的结果，并且在稀薄流域中能够获得优于N-S方程的结果，有效改善了N-S方程对强非线性流动描述的不足并极大拓展非平衡流动模拟的范围，具有进行大规模实际工程应用的能力[13]。黄依峰等[14]运用NCCR模型对不同来流高度下的侧向喷流问题进行模拟计算，并与N-S方程和DSMC方法结果进行对比，结果表明NCCR模型结果更为贴近DSMC结果。曹竣哲等[15]通过一系列典型非平衡流动数值模拟定量验证了NCCR模型的准确性。
基于此，本文通过将NCCR方程耦合Maxwell电磁场控制方程，发展了考虑电磁源项的多组分NCCR-MHD方程，同时加入Park TTv双温度模型以及Park11组分化学反应模型，建立了低磁雷诺数高速磁流体热化学非平衡数值模拟方法，研究磁场的存在以及磁感应强度的大小对高速磁流体流动特性的影响机理，同时探究了在不同高度环境、马赫数下磁场的作用效果。
1. 计算方法与物理模型
1.1 考虑电磁源项的多组分NCCR方程理论
NCCR方程最先由Eu[16]根据广义流体动力学理论建立，之后针对热化学非平衡多组分混合气体流动问题，Ahn[17]在单组分NCCR方程基础上建立了包含单原子和双原子分子的多组分非线性耦合本构模型，加入电磁源项后守恒量方程为：
\begin{split} &\frac{\partial }{\partial t} \left(\begin{gathered}\rho \\ \rho {\boldsymbol{u}}\\ \rho E\\ {\rho }_{i}\\ \end{gathered}\right)+\nabla \cdot \left(\begin{gathered}\rho {\boldsymbol{u}}\\ \rho {\boldsymbol{uu}}\\ \left(\rho E+p\right){\boldsymbol{u}}\\ {\rho }_{i}{\boldsymbol{u}}\\\end{gathered}\right)+ \nabla \cdot \left(\begin{gathered}0\\ {\displaystyle \sum {}_{i = 1}^{r}\left({{\boldsymbol{\varPi }} }_{i}+\omega {\varDelta }_{i}{\boldsymbol{I}}\right)}\\ {\displaystyle \sum {}_{i = 1}^{r}\left({\boldsymbol{\varPi } }_{i}+\omega {\varDelta }_{i}{\boldsymbol{I}}\right)\cdot {\boldsymbol{u}}+{\boldsymbol{Q}}}\\ \frac{{\rho }_{i}}{\rho }{D}_{c,i}{c}_{c,i}\\\end{gathered}\right) \\ &=\left(\begin{gathered}0\\ 0\\ 0\\ {S}_{i}\\\end{gathered}\right)+ {Q}_{m}\cdot \left(\begin{gathered}0\\ {\boldsymbol{J}}\times {\boldsymbol{B}}\\ {\boldsymbol{J}}\cdot {\boldsymbol{E}}\\ 0\\\end{gathered}\right) \end{split} (1) 式中：下标i代表某一组分； {\boldsymbol{u}}、p、E 分别为多组分混合气体的平均速度、压力和总能；{\boldsymbol{\varPi }}为黏性应力，\varDelta 为附加体积正应力，{\boldsymbol{Q}}为热通量；{D_{c,i}}为组分i的扩散系数，{c_{c,i}}为组分i的质量分数，{S_i}为化学反应源项；方程右端第二项为电磁源项，{Q_m}为磁相互作用数，{\boldsymbol{J}}为电流密度，{\boldsymbol{B}}为磁感应强度，{\boldsymbol{E}}为电场强度。
多组分混合气体非守恒量本构方程[18]由一组非线性耦合微分方程组成：
- 2\left( {p + \varDelta } \right){\left[ {\nabla {\boldsymbol{u}}} \right]^{\left( 2 \right)}} - 2{\left[ {\boldsymbol{\varPi }\cdot \nabla {\boldsymbol{u}}} \right]^{\left( 2 \right)}} - \frac{p}{{{\eta _{\text{b}}}}}{\boldsymbol{\varPi }}q\left( \kappa \right) = 0 (2) - 2\gamma '\left( {\Delta {\boldsymbol{I}} + {\boldsymbol{\varPi }}} \right):\nabla {\boldsymbol{u}} - \frac{2}{3}\gamma 'p\nabla \cdot {\boldsymbol{u}} - \frac{2}{3}\gamma '\frac{p}{{{\eta _b}}}\Delta q\left( \kappa \right) = 0 (3) \left( {p + \varDelta } \right){c_p}T\nabla \ln T + {\boldsymbol{\varPi }}{c_p}\nabla T + {\boldsymbol{Q}}\nabla {\boldsymbol{u}} + \frac{{p{c_p}T}}{\lambda }{\boldsymbol{Q}}q\left( \kappa \right) = 0 (4) 式中：q\left( \kappa \right) = \sinh \kappa /\kappa ，\kappa 由Rayleigh-Onsager为耗散函数给定， \gamma ' = (5 - 3\gamma )/2 （\gamma 为比热比）， {\eta _b} 为附加应力黏性系数，{c_p}为定压比热。
通过进一步将输运方程无量纲化，可得到NCCR本构方程：
\varPi q(c R)=\left(1+f_b \Delta\right) \varPi_0+[\varPi \cdot \nabla u]^{(2)} (5) \Delta q(c R)=\Delta_0+\frac{3}{2} f_b\left(\Pi+f_b+\Delta I\right): \nabla u (6) Q q(c R)=\left(1+f_b \Delta\right) Q_0+\Pi \cdot Q_0+Q \cdot \nabla u (7) 式中： c 为分子模型参数，R为无量纲Rayleigh-Onsager耗散函数，{{\boldsymbol{\varPi }}_0}为牛顿黏性应力， {\varDelta _0} 为线性附加正应力，{{\boldsymbol{Q}}_0}为傅里叶热传导。NCCR模型和Eu广义流体动力学方程共同组成了NCCR基本理论体系[19]。
本文采用文献[18]的混合模态间断伽辽金算法对NCCR方程进行求解。相比于牛顿黏性定律和傅里叶热传导定律，NCCR方程是强非线性方程，传统的FVM对NCCR模型的求解效果并不是特别理想，而混合间断伽辽金算法可以使得高阶量和守恒量保持同一高度，同时只需要定义守恒变量的边界条件即可[18]。同时为了考虑高速流动中的热不平衡现象，采用ParkTTv双温度模型，假定组分的平移和旋转能量模式在一个温度Tt下处于平衡状态，组分的振动和电子能量模式在另一个温度Tv下处于平衡状态[20]。
1.2 化学反应模型
设定高速来流混合气体组分数为ns，化学反应数目为nr，其通用化学反应方程式如下[21]：
{\displaystyle \sum _{s = 1}^{{n}_{s}}{a}_{s,r}}{Z}_{s}\underset{{k}_{{\mathrm{b}},r}}{\overset{{k}_{{\mathrm{f}},r}}{\rightleftharpoons }}{\displaystyle \sum _{s = 1}^{{n}_{s}}{b}_{s,r}}{Z}_{s} (8) 式中： r = 1,2,3, \cdots ,{n_r} ， {a_{s,r}} 和 {b_{s,r}} 分别为组分s在第r反应式中为反应物和生成物的化学反应计量系数；下标f对应正向，下标b对应逆向， {k_{{\mathrm{f}},r}} 和 {k_{{\mathrm{b}},r}} 分别为第r个化学反应的正向和逆向化学反应速率。对于混合气体中的组分 {Z_s} ，其质量生成率 {\dot w_s} 计算公式如下：
{\dot w_s} = {M_s}\sum\limits_{r = 1}^{n_r} {\left( {{b_{s,r}} - {a_{s,r}}} \right)} \left( {{R_{{\mathrm{f}},r}} - {R_{{\mathrm{b}},r}}} \right) (9) \left\{ \begin{gathered} {R_{{\mathrm{f}},r}} = {k_{{\mathrm{f}},r}}\prod\limits_{s = 1}^{n_s} {{{\left( {\frac{{{\rho _s}}}{{{M_s}}}} \right)}^{{a_{s,r}}}}} \\ {R_{{\mathrm{b}},r}} = {k_{{\mathrm{b}},r}}\prod\limits_{s = 1}^{n_s} {{{\left( {\frac{{{\rho _s}}}{{{M_s}}}} \right)}^{{b_{s,r}}}}} \\ \end{gathered} \right. (10) 式中： {M_s} 为组分s的摩尔质量。化学反应速率 {k_{{\mathrm{f}},r}} 和 {k_{{\mathrm{b}},r}} 由Arrhenius公式给出：
\left\{ \begin{gathered} {k_{\mathrm{f}}} = {A_ {\mathrm{f}} }{T^{B_{\mathrm{f}}}}\exp \left( { - {{{C_{\mathrm{f}}}} \mathord{\left/ {\vphantom {{{C_{\mathrm{f}}}} T}} \right. } T}} \right) \\ {k_{\mathrm{b}}} = {A_{\mathrm{b}}}{T^{B_{\mathrm{b}}}}\exp \left( { - {{{C_{\mathrm{b}}}} \mathord{\left/ {\vphantom {{{C_{\mathrm{b}}}} T}} \right. } T}} \right) \\ \end{gathered} \right. (11) {K_c} = \frac{{{k_{\mathrm{f}}}}}{{{k_{\mathrm{b}}}}} (12) 式中：T为温度，A为频率因子，B为温度指数，C为组分反应活化温度， {K_c} 为化学反应平衡常数。
1.3 电动力学模型
假设等离子体微元呈现电中性，则电流密度{\boldsymbol{J}}满足连续性方程[22]:
\nabla \cdot {\boldsymbol{J}} = 0 (13) 由广义欧姆定律可得电流密度{\boldsymbol{J}}为：
{\boldsymbol{J}} = \sigma \left( {{\boldsymbol{E}} + {\boldsymbol{u}} \times {\boldsymbol{B}}} \right) (14) 式中\sigma 为气体电导率；针对定常外磁场，由法拉第定律 \nabla \times {\boldsymbol{E}} = {{ - \partial {\boldsymbol{B}}} \mathord{\left/ {\vphantom {{ - \partial {\boldsymbol{B}}} {\partial t}}} \right. } {\partial t}} = 0 ，可得电场是无旋的，因此可以写成电势函数形式：{\boldsymbol{E}} = - \nabla \phi ，代入式（13）和（14）可得：
\nabla \cdot \left( {\sigma \nabla \phi } \right) = \nabla \cdot \left[ {\sigma \left( {{\boldsymbol{u}} \times {\boldsymbol{B}}} \right)} \right] (15) 本文电导率模型采用Bush模型，即：
\sigma = {\sigma _0} \cdot {\left( {\frac{T}{{{T_0}}}} \right)^n} (16) 式中：{\sigma _0}为参考电导率，{T_0}为参考温度。引入虚拟时间项得：
\frac{{\partial \phi }}{{\partial t}} + \nabla \cdot \left( {\sigma \nabla \phi } \right) = \nabla \cdot \left[ {\sigma \left( {{\boldsymbol{u}} \times {\boldsymbol{B}}} \right)} \right] (17) 采用隐式时间离散式（17），得到电势函数\phi 和感应电场{\boldsymbol{E}}，在由式（14）得电流密度{\boldsymbol{J}}。
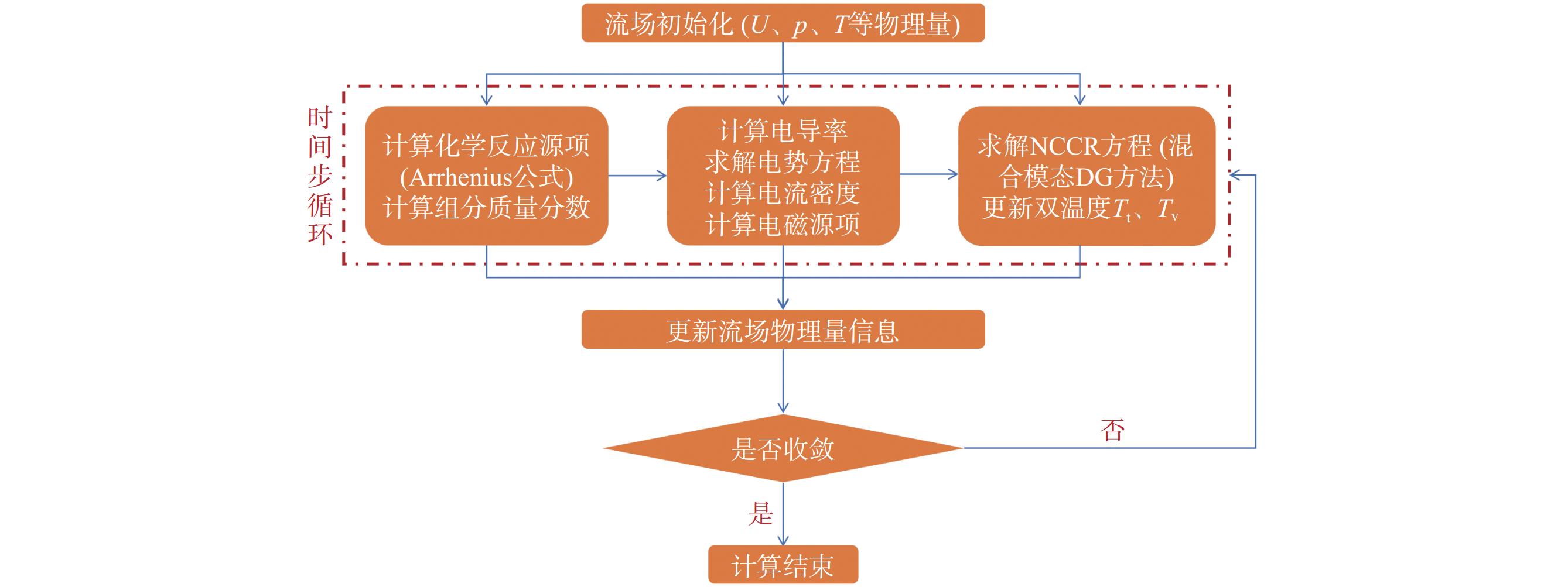
结合前面几个小节内容，整个NCCR-MHD求解流程如图1所示。
1.4 数值方法验证
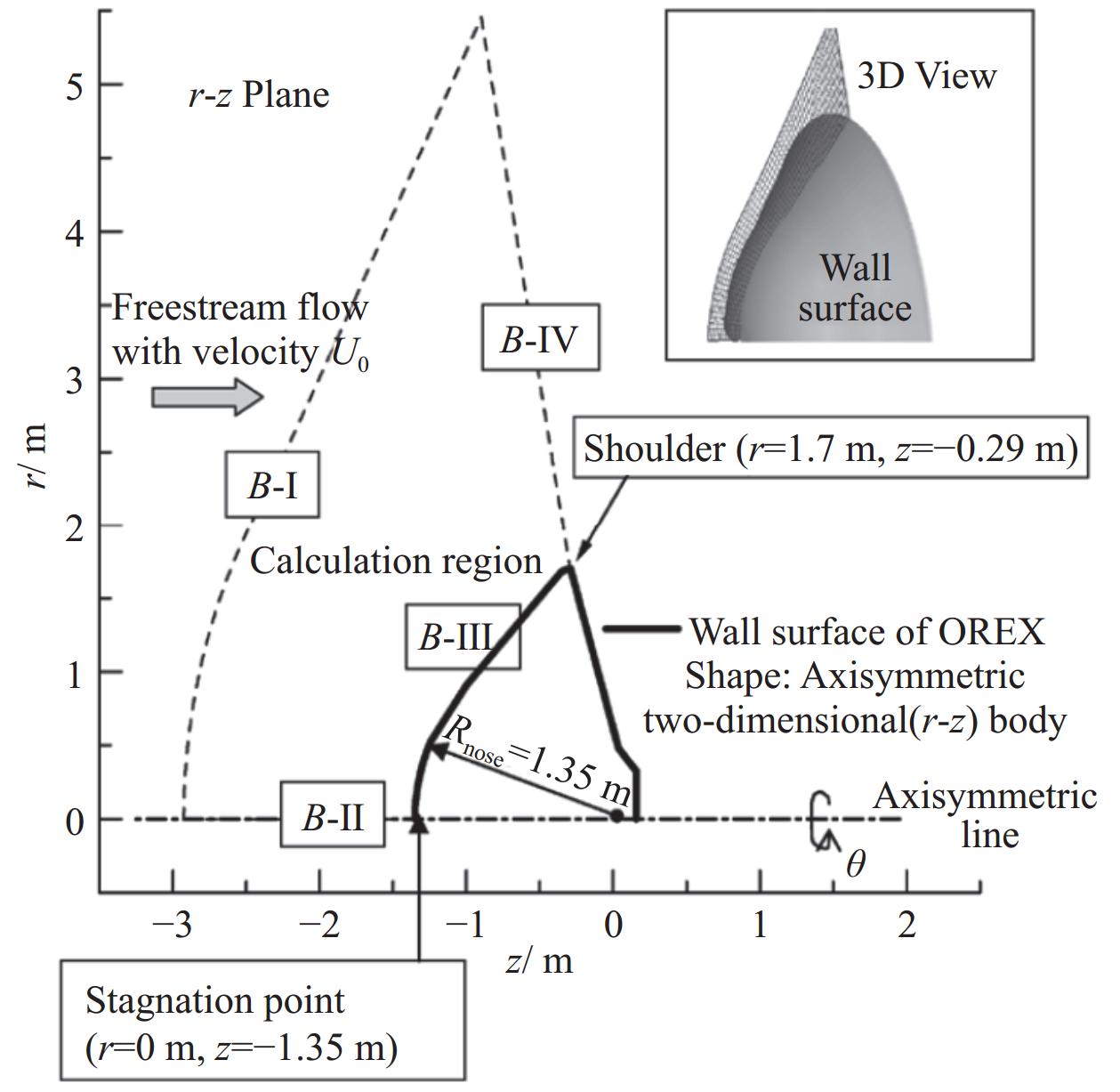
关于间断伽辽金算法求解NCCR方程的验证本团队已在文献[17]中给出，现验证本文所建立的NCCR-MHD耦合方法准确性。采用文献[2]中的OREX返回舱算例进行验证，返回舱几何尺寸如图2所示，计算网格同文献采用二维半模网格，远场入口为自由来流边界条件，壁面为固定壁温、无滑移、非催化壁面，来流压力{p_\infty } = 23.6 Pa，温度{T_\infty } = 248.12 K，速度U =
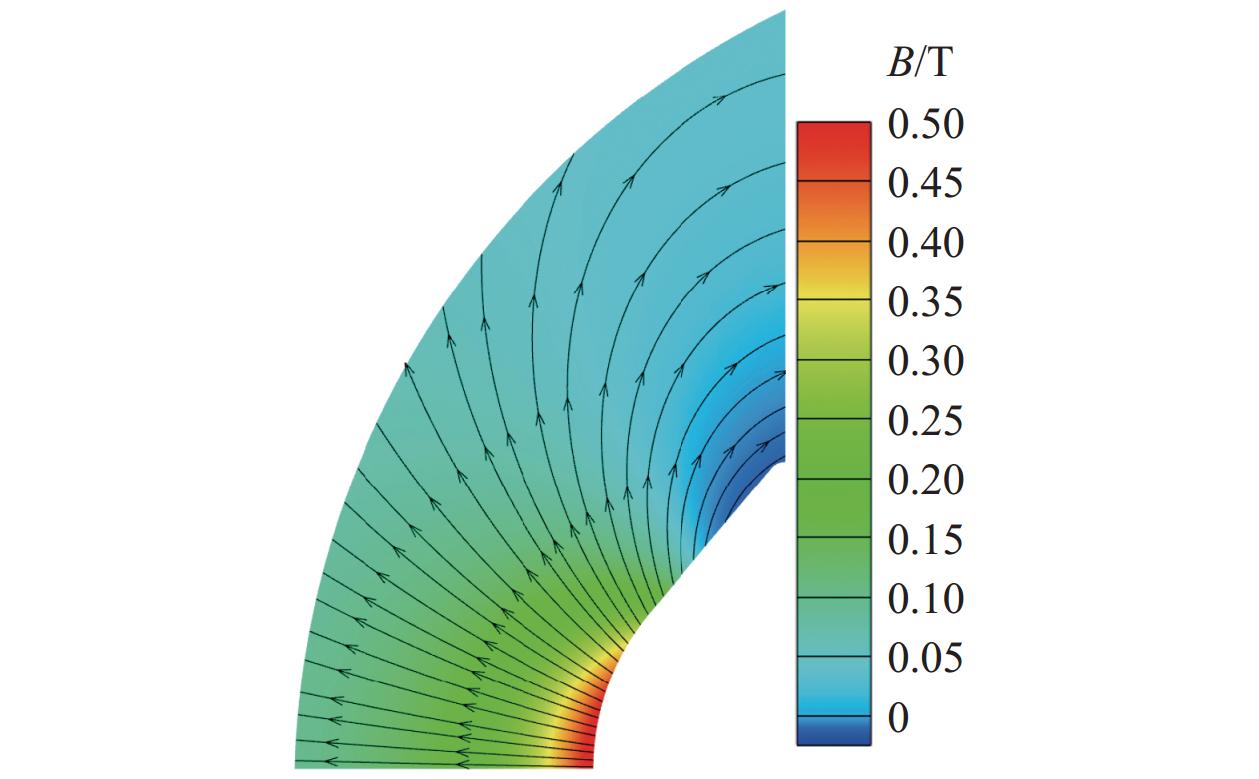
5561.6 m/s，壁面温度为1519 K。外加磁场为偶极子磁场，磁场分布由公式（18）给出，滞止点{B_0} = 0.5 T，磁场磁感线分布如图3所示。![]()
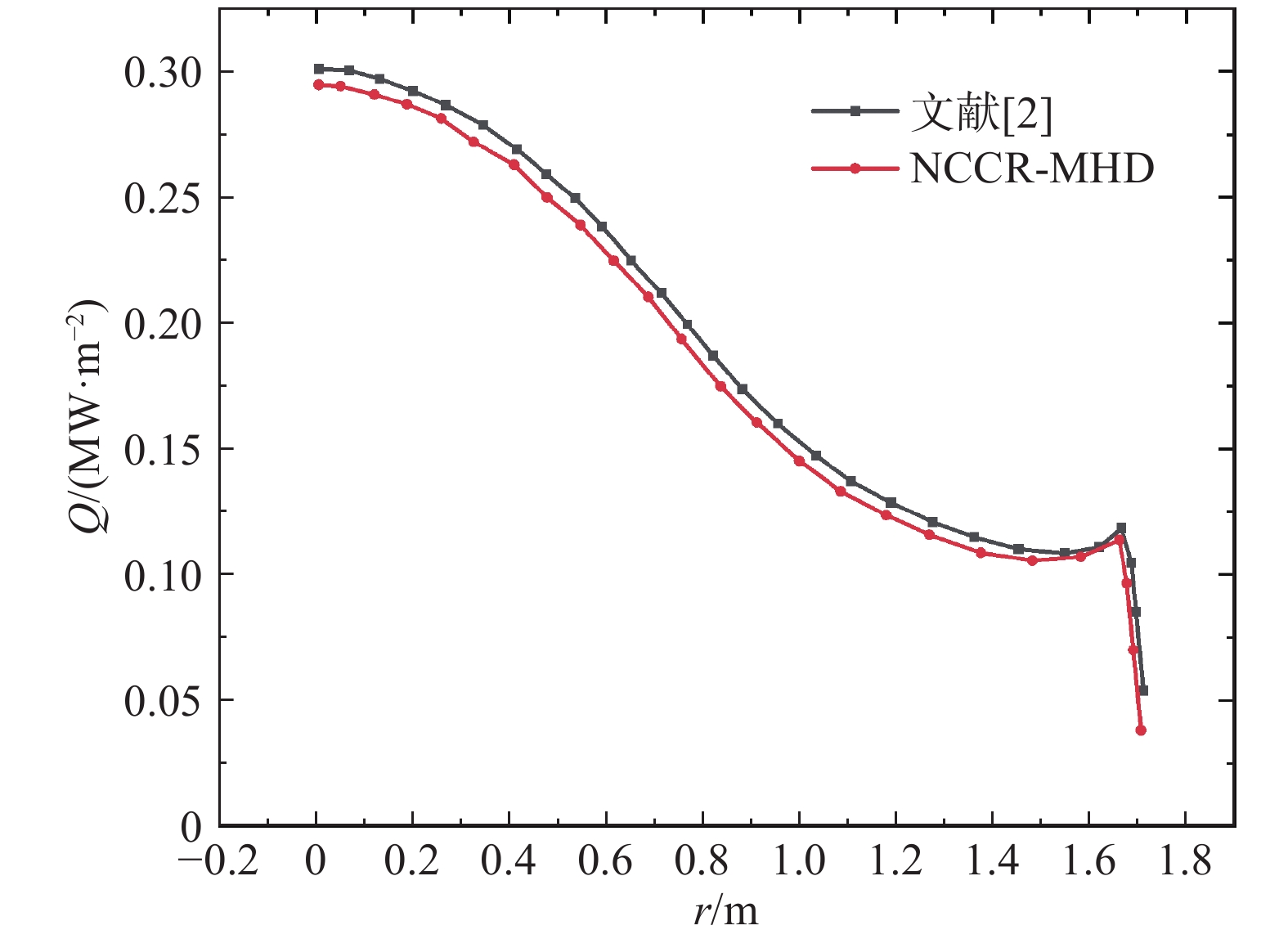
图 3 OREX返回舱周围磁场分布Figure 3. Distribution of the magnetic field around the OREX re-entry capsule\begin{split} {B_r} = &- \frac{{{B_0}R_b^3}}{{2{{({z^2} + {r^2})}^{3/2}}}}\frac{{3zr}}{{{z^2} + {r^2}}} \\ {B_z} = &- \frac{{{B_0}R_b^3}}{{2{{({z^2} + {r^2})}^{3/2}}}}\left(\frac{{2{z^2} - {r^2}}}{{{z^2} + {r^2}}}\right) \end{split} (18) 图4 为OREX返回舱壁面热流分布曲线，对比了本文NCCR-MHD数值模拟结果和文献数据。可以看出，在相同磁场配置下，本文计算结果略低于文献值。根据文献[18]的分析可知，这一差异源于NCCR方程考虑了稀薄气体的热非平衡特性，其包含了N-S方程所忽略的非线性项，因此由NCCR方程计算得出的热流值略小于N-S方程计算得到的热流值。
![]()
图 4 OREX返回舱壁面热流分布曲线Figure 4. Wall heat flux distribution curve of OREX return capsule2. 高速磁流体圆柱扰流数值模拟
2.1 网格无关性验证
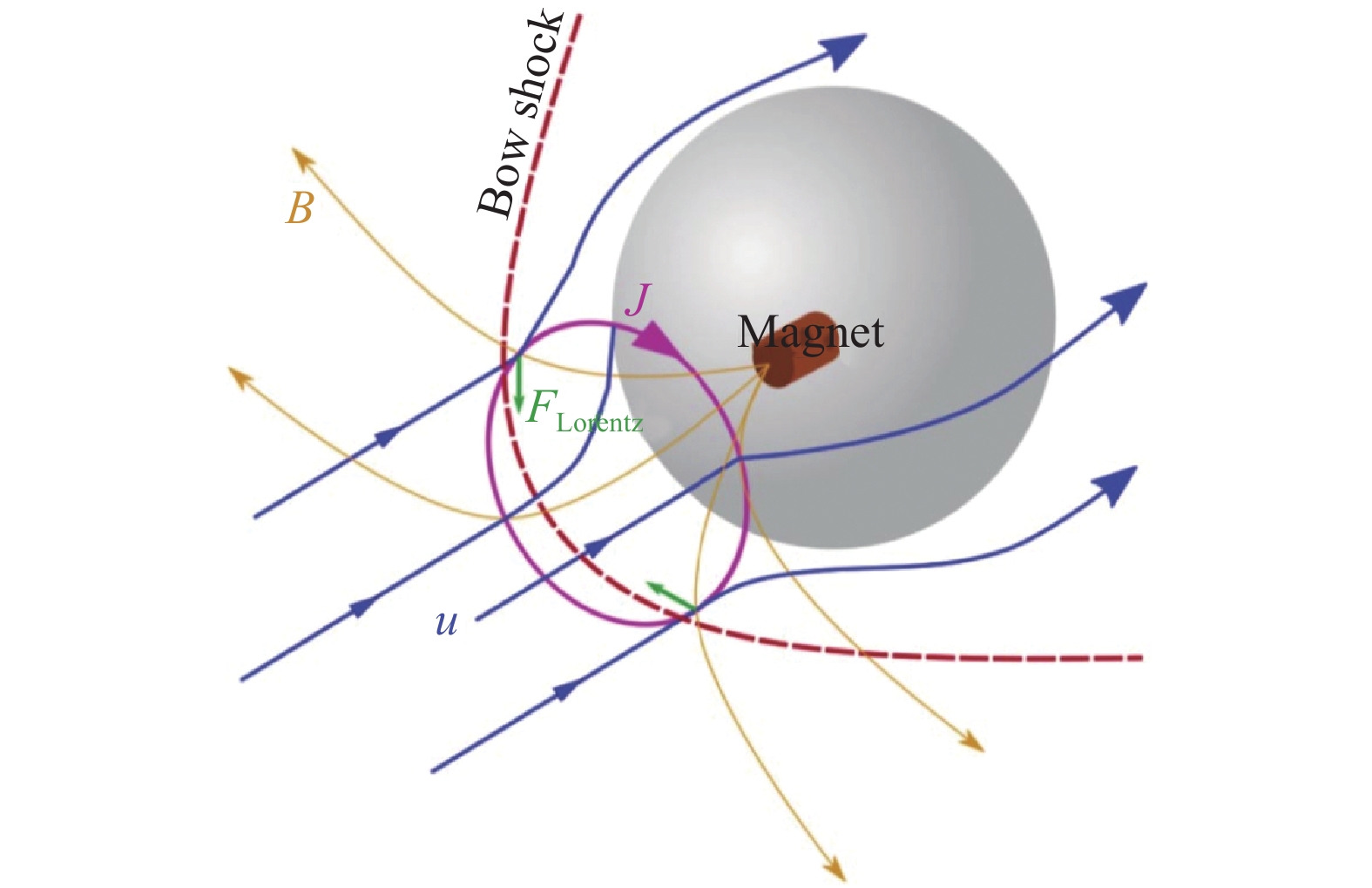
如图5所示，磁控热防护的原理是在高速等离子体流场中施加磁场，改变粒子的运动状态，将激波远离壁面，进而达到热防护的目的。本文基于上述开发的程序，以高速等离子体二维圆柱绕流为对象，探究磁控热防护的作用机理，着重探讨磁场强度、来流马赫数和来流高度对流场结构以及磁控热防护作用效果的影响。
![]()
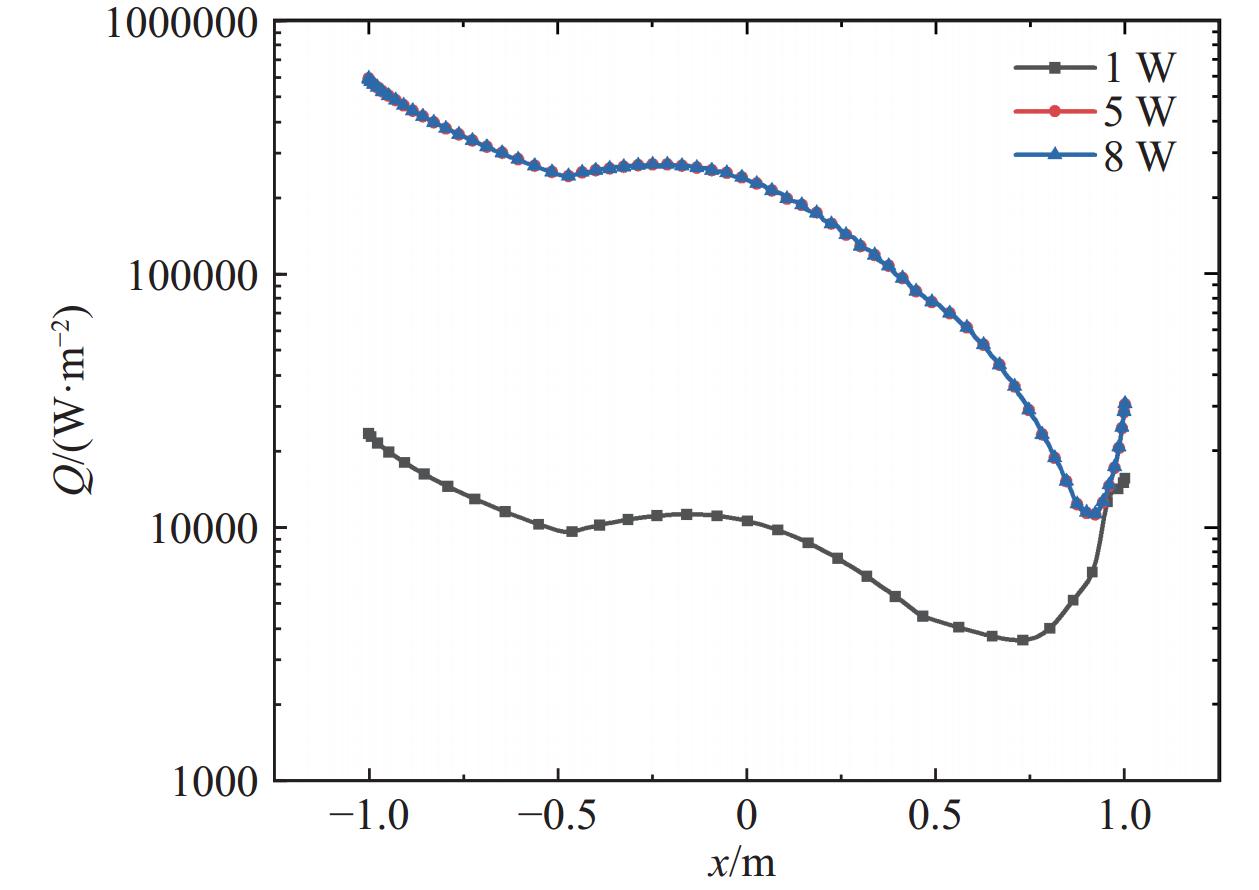
图 5 磁场作用下的等离子体球体扰流示意图[8]Figure 5. Schematic diagram of plasma sphere flow disturbance under magnetic field effects由于圆柱构型以及流场均具有对称性，为简化计算，网格无关性验证采用轴对称二维网格，即1/2流场。其中粗网格（网格数量为1 W）无附面层，中网格（网格数量为5 W）第一层网格高度为0.001 m，细网格（网格数量为8 W）第一层网格高度为
0.00001 m。图6可以看出，中网格和细网格条件下壁面热流密度分布结果几乎重合，表明当网格数量达到8 W时，壁面热流分布基本趋于稳定，不再随网格数量的变化而变化。因此，本文统一采用细网格（全流场网格数量为16 W）进行计算分析。![]()
图 6 不同网格数量壁面热流密度分布Figure 6. Wall heat flux distribution curve on the wall with different grid2.2 磁感应强度对热化学非平衡流动的影响
首先探究磁场的存在以及驻点磁感应强度大小对高速磁流体热化学非平衡流动的影响机理，圆柱半径R = 1 m，外加磁场为偶极子磁场，驻点磁感应强度为{B_0}，磁场分布由式（18）给出，来流压力p = 20 Pa，温度T = 223 K，速度U =
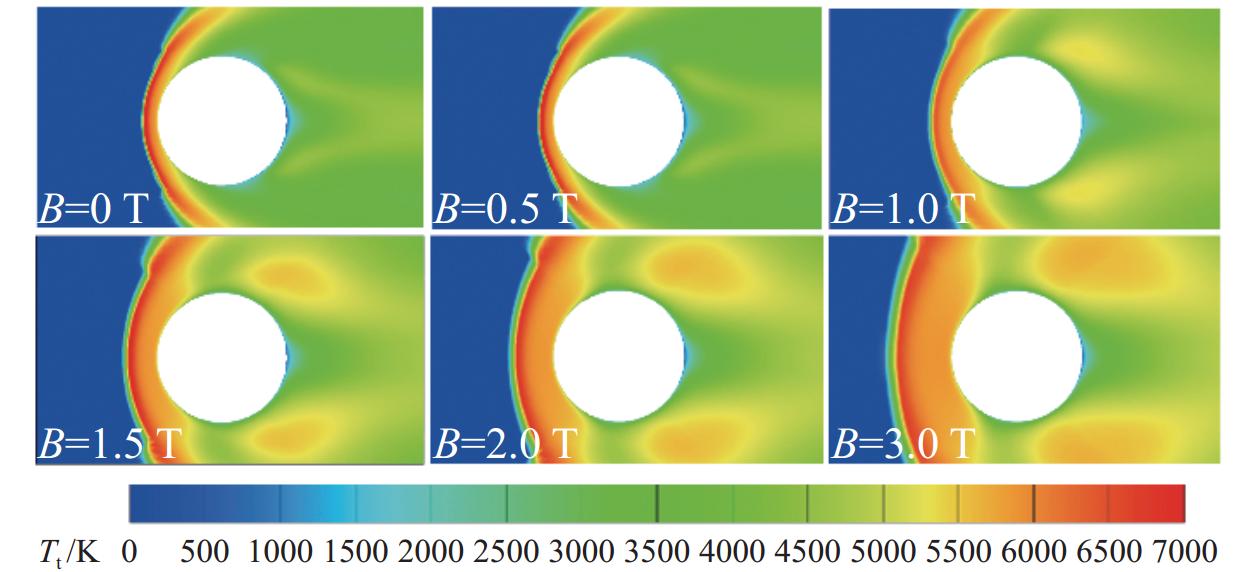
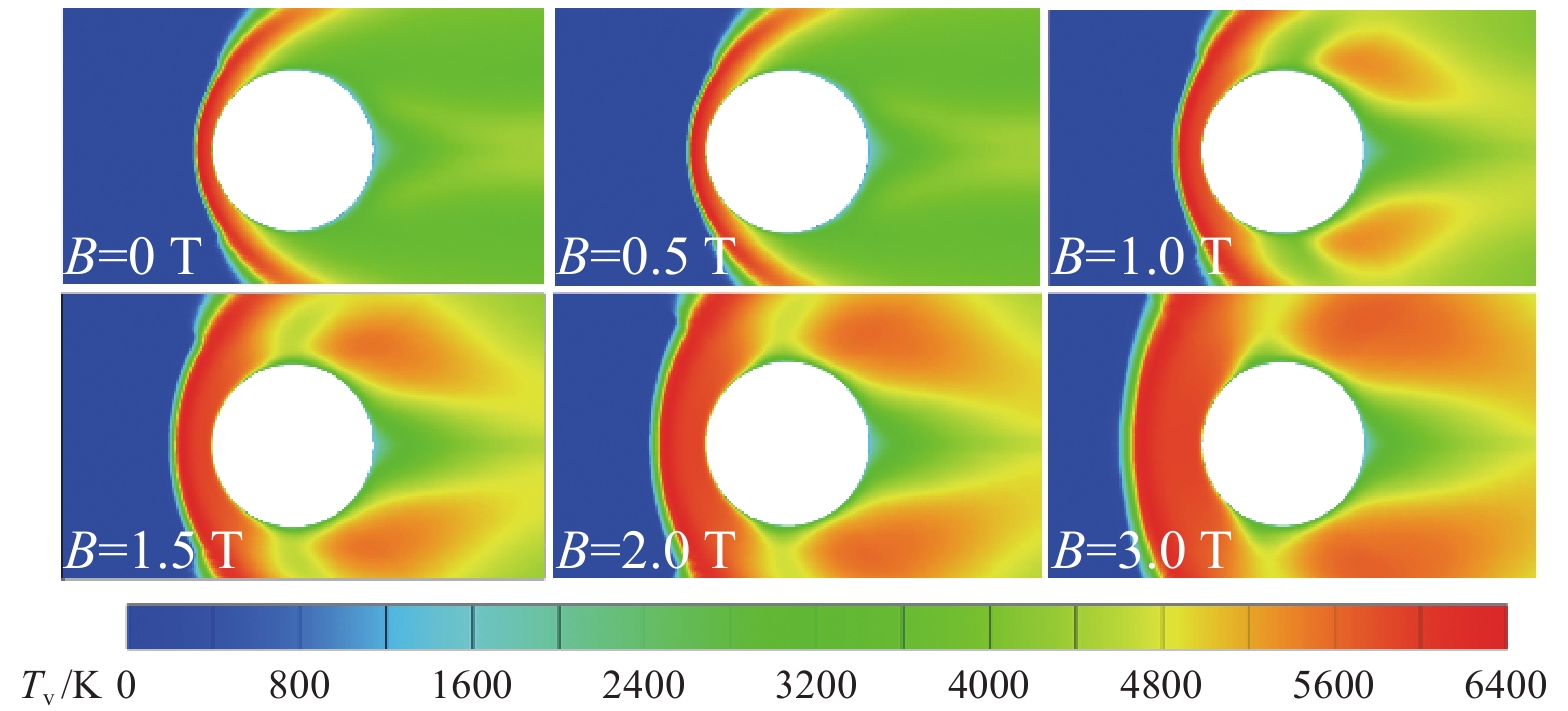
6000 m/s；采用无滑移、固定壁温非催化壁面，壁面温度为300 K，采用Park11组分化学反应模型，自由来流N2摩尔分数为0.2，O2摩尔分数为0.8；不考虑霍尔效应的影响，驻点磁感应强度{B_0}分别设置为0、0.5、1、1.5、2、3 T。{\boldsymbol{B}} = {B_0}\frac{{R_b^2}}{{{r^2}}}\left[ {\left( {\cos {\theta ^2} - \sin {\theta ^2}} \right){{\boldsymbol{e}}_x} + \sin (2\theta) {{\boldsymbol{e}}_y}} \right] (19) 图7和图8分别为不同磁感应强度下的圆柱扰流平动温度云图和振动温度云图。结果显示，高速来流经过圆柱前缘脱体激波后，气流被剧烈压缩，导致温度急剧上升。当平动温度达到足够高时，气体各组分振动能开始被激发，振动温度升高，同时吸收部分平动能，因此可以观察到波后气体平动温度具有下降的趋势。同时，由图还可以看出激波脱体距离受磁感应强度大小影响显著：当磁感应强度B0 = 0 T时，激波距离壁面较近，随着磁感应强度增大，激波脱体距离不断增大。此外，磁感应强度对脱体激波形状影响也较为显著，当磁感应强度较小时，脱体激波上下两侧偏折角度较大，向壁面靠拢；当磁感应强度较大时，脱体激波上下两侧偏折角度较小，形态更接近正激波。
![]()
图 7 不同磁感应强度下的平动温度云图Figure 7. Translational temperature contours with different magnetic induction intensities![]()
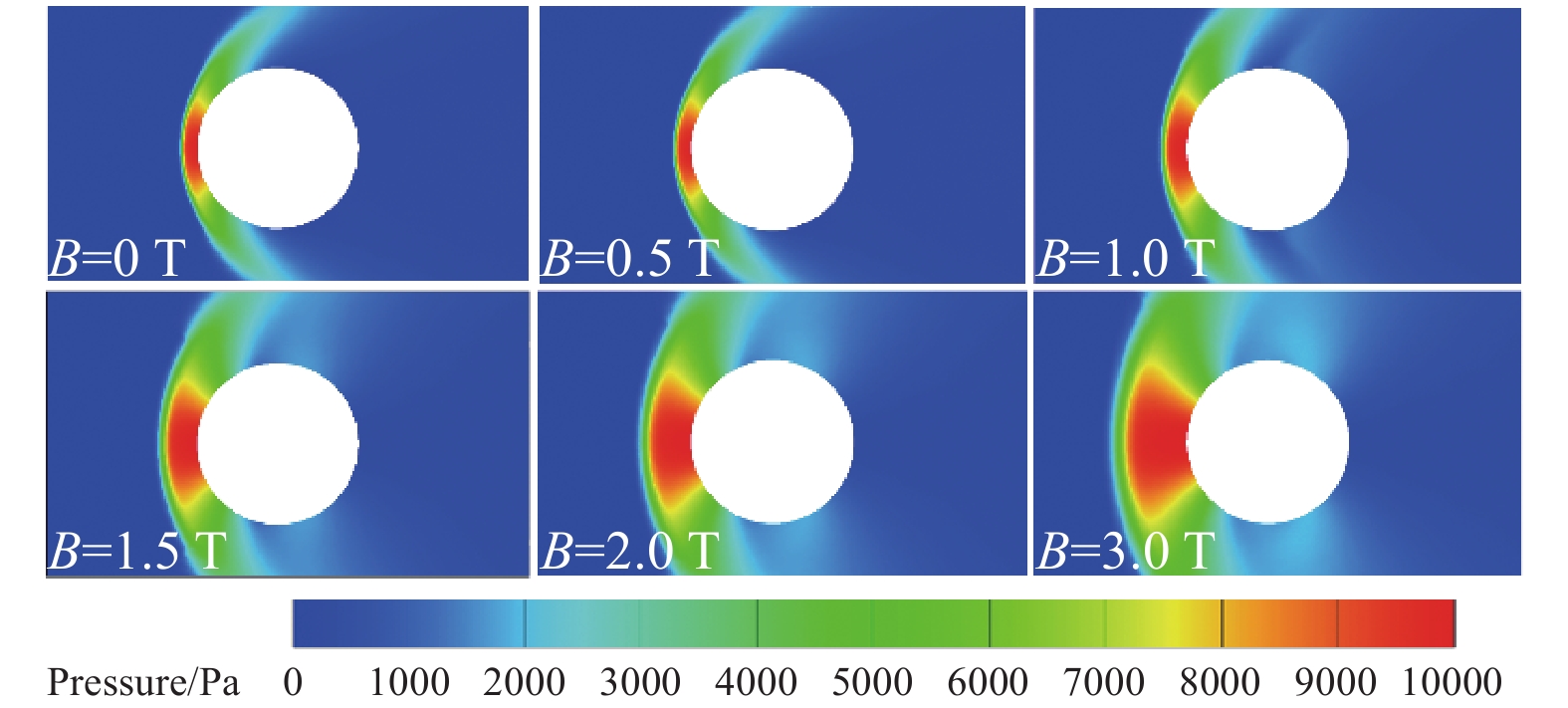
图 8 不同磁感应强度下的振动温度云图Figure 8. Vibration temperature contour with different magnetic induction intensities图9给出了不同磁感应强度下的圆柱扰流压力云图。由图可以看出，高速气流经过脱体激波后被剧烈压缩，导致压力急剧升高，在圆柱前缘形成伞状高压区，被称为“磁阻力伞”。同时随着磁感应强度的增大，激波脱体距离增加，高压区不断扩大，圆柱的阻力不断增大，这对返回舱再入过程是有利的。返回舱再入时速度很高，具有巨大的动能，重返大气层时需要依靠前缘阻力把速度降下来，将动能迅速转化为热能并耗散掉。
![]()
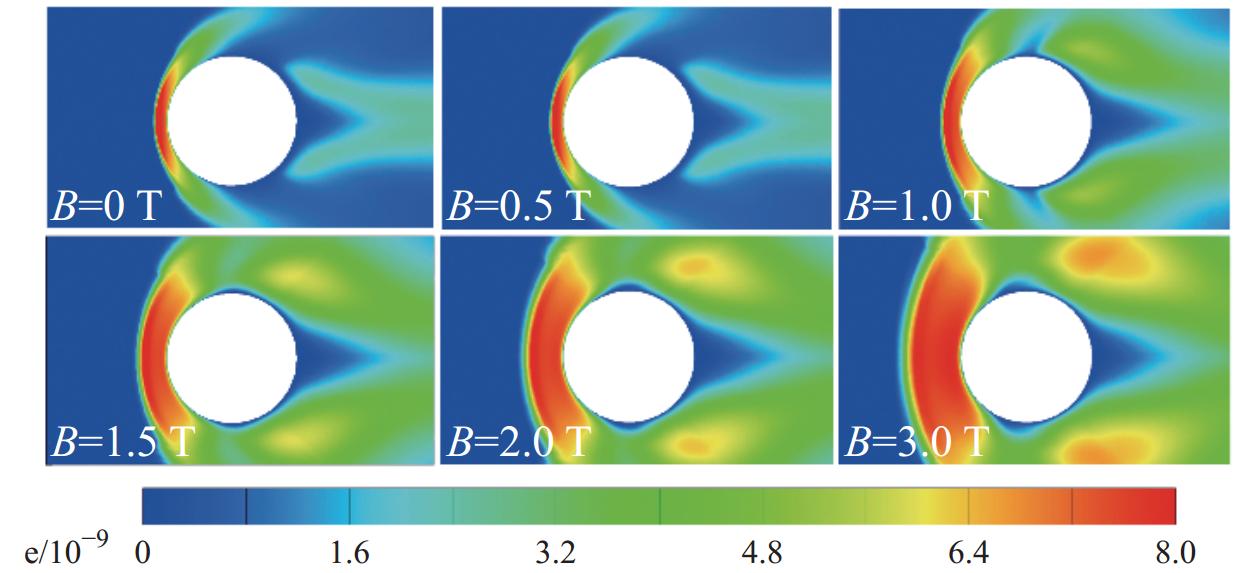
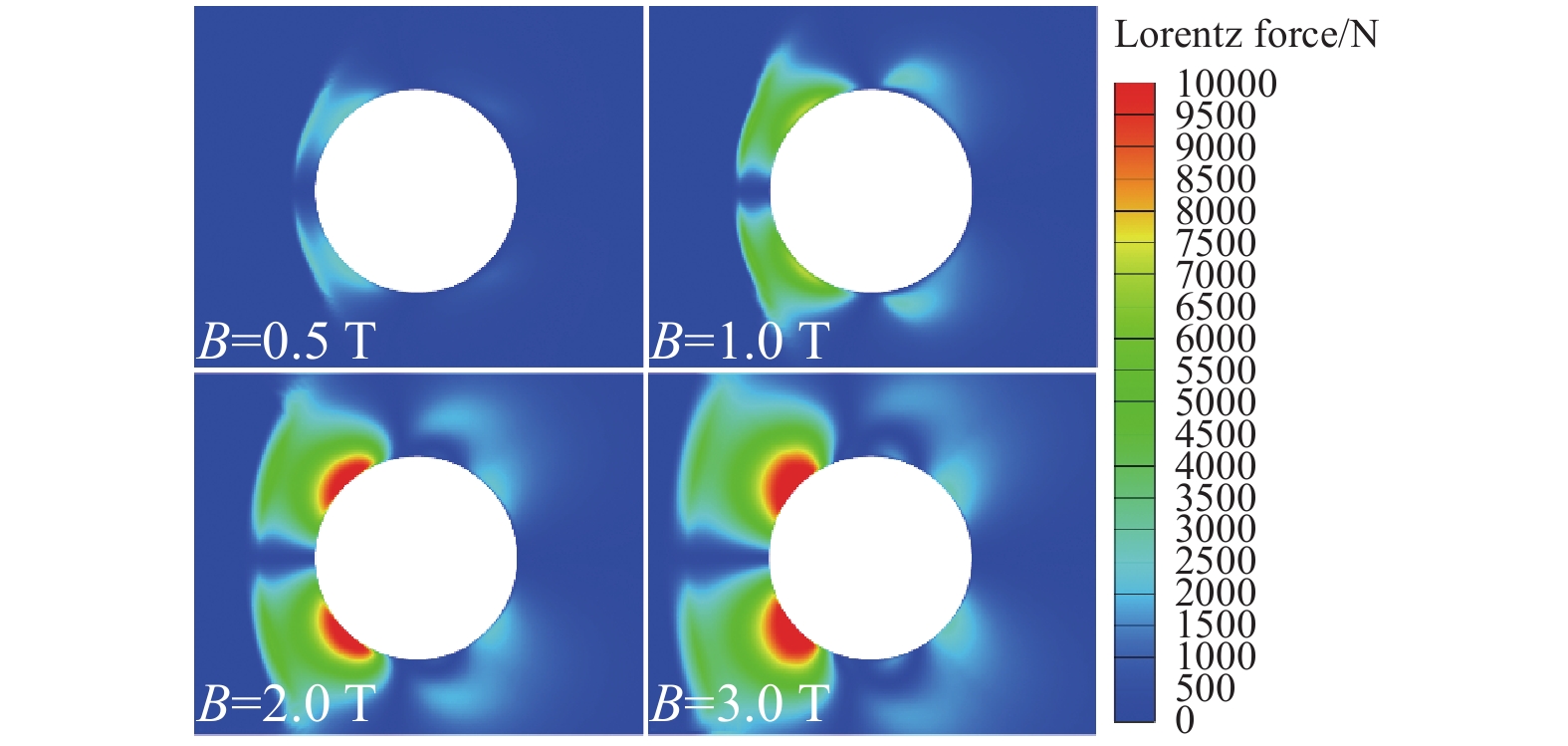
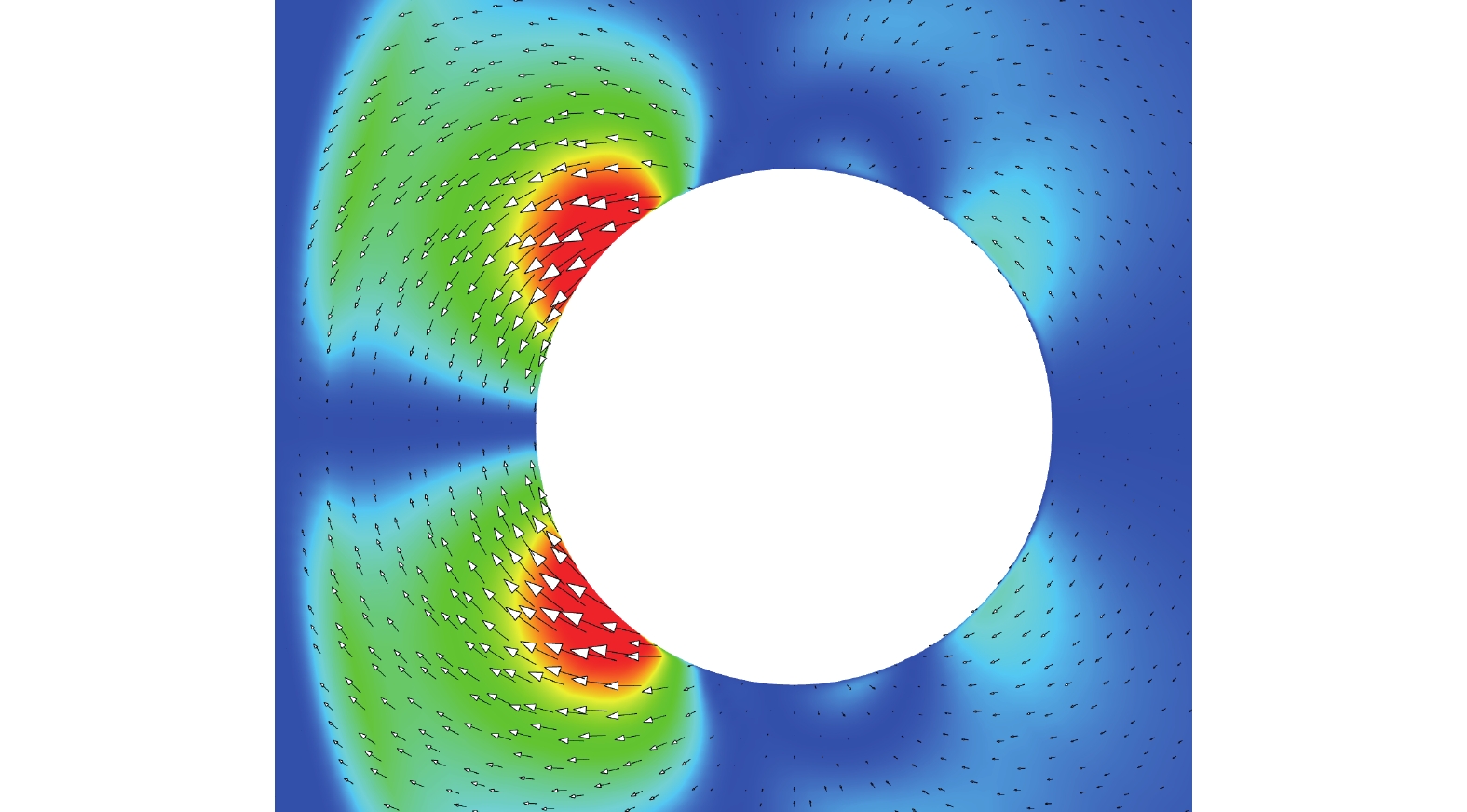
图 9 不同磁感应强度下的压力云图Figure 9. Pressure contours at different magnetic induction intensities图10为不同磁感应强度下的电子摩尔分数云图。可见电子浓度较高区域主要集中在弓形激波后，这是由于激波后温度急剧升高引发气体离解、电离、复合等一系列化学反应所致。当磁感应强度B0 = 0 T时，电子分布较为集中且距离壁面较近；由图11可以看出，随着磁感应强度的不断增大，电子受到的洛伦兹力越来越大，同时作用范围不断扩大，受力主要分布在圆柱前缘两侧。图12给出B0 = 3 T时洛伦兹力矢量图分布。在圆柱前缘两侧，洛伦兹力方向指向前缘滞止线，将其沿流向和法向分解，其中，逆流向洛伦兹力分量主要作用是做负功，导致流体减速，激波脱体距离增大；法向洛伦兹力虽不对流体做功，却使得流线偏转，改变激波形状，磁场越强，激波形状变化越大。
![]()
图 10 不同磁感应强度下的电子摩尔分数云图Figure 10. Electron mole fraction contour with different magnetic induction intensities![]()
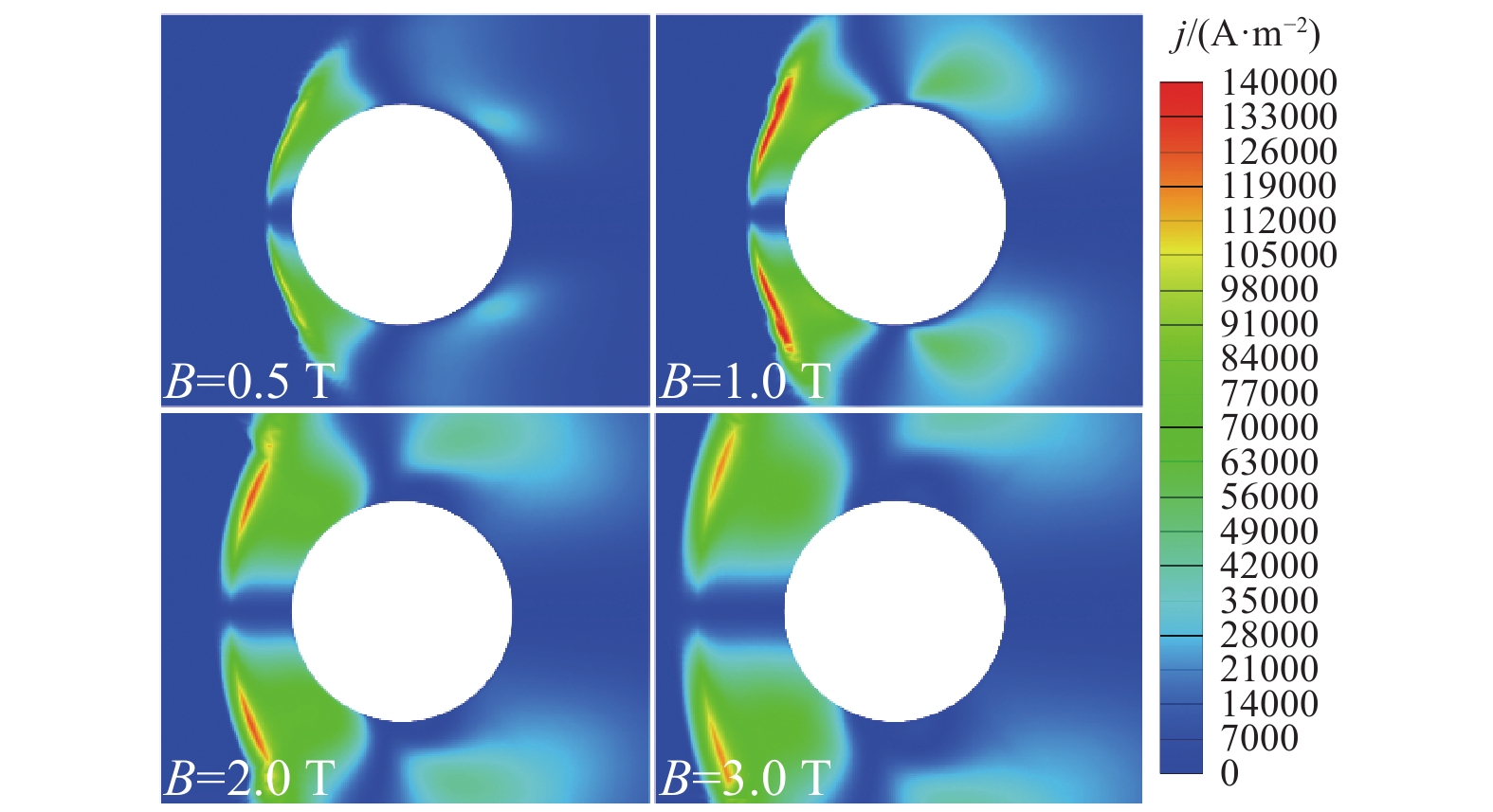
图 11 不同磁感应强度下的洛伦兹力分布云图Figure 11. Lorentz force distribution contour with different magnetic induction intensities图13为不同磁感应强度下的电流密度分布云图。电流密度较大区域主要位于激波后，这是由于气流经过激波后速度降低，紧邻激波处高速气流产生的感应电动势较大，因此所产生感应电流也较大。波后电流密度峰值随着磁感应强度的增大呈现先增大后减小的趋势。
![]()
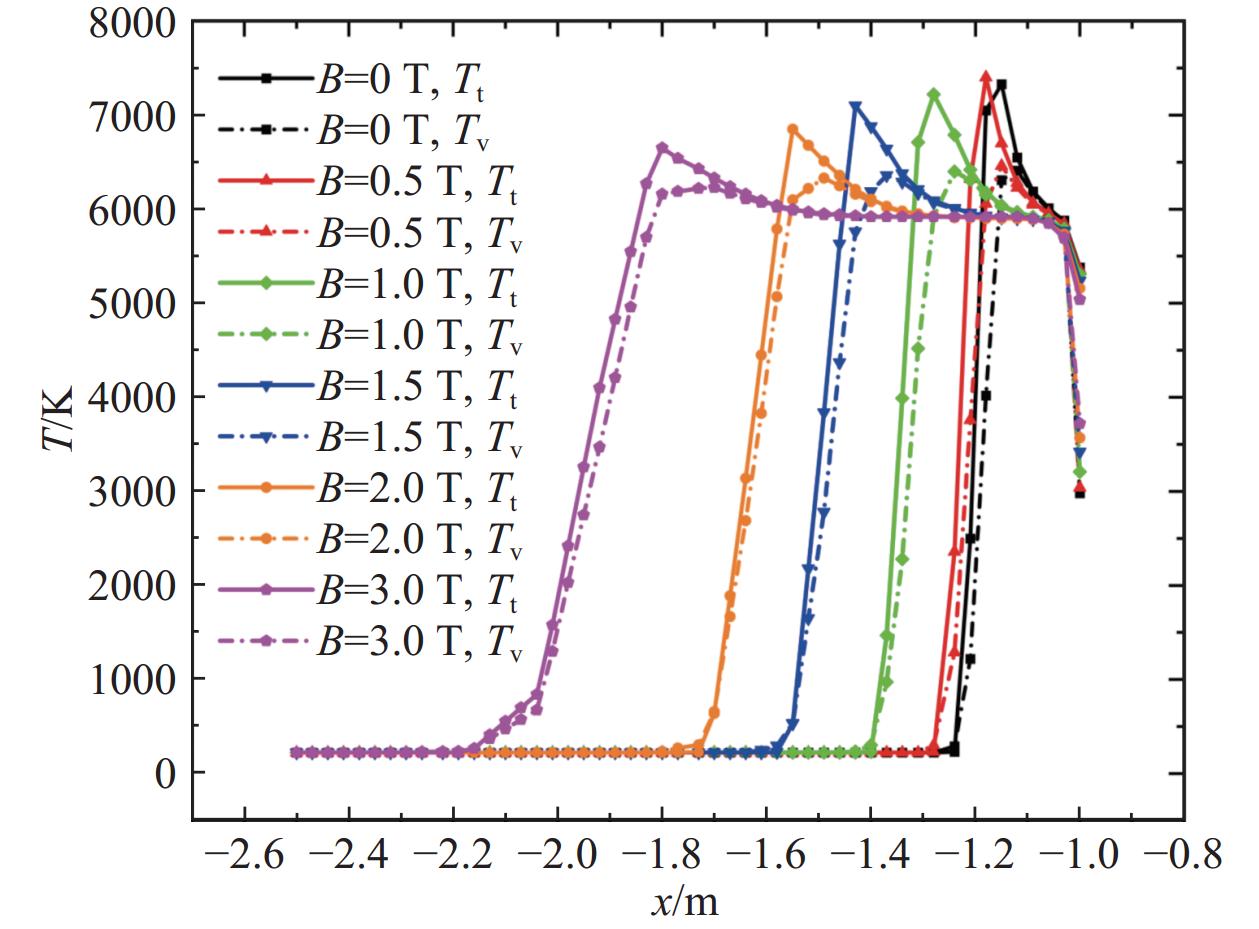
图 13 不同磁感应强度下的电流密度分布云图Figure 13. Contour of current density distribution with different magnetic induction intensities图14进一步展示了不同磁感应强度下的圆柱前缘滞止线平动温度和振动温度分布。由图可以看出，随着磁感应强度的不断增加，激波脱体距离不断增加。如，B0 = 0.5 T时相对于无磁场，激波脱离距离增加了14.28%；而当B0 = 3 T时，相对于无磁场，激波脱体距离增加了452.38%。
![]()
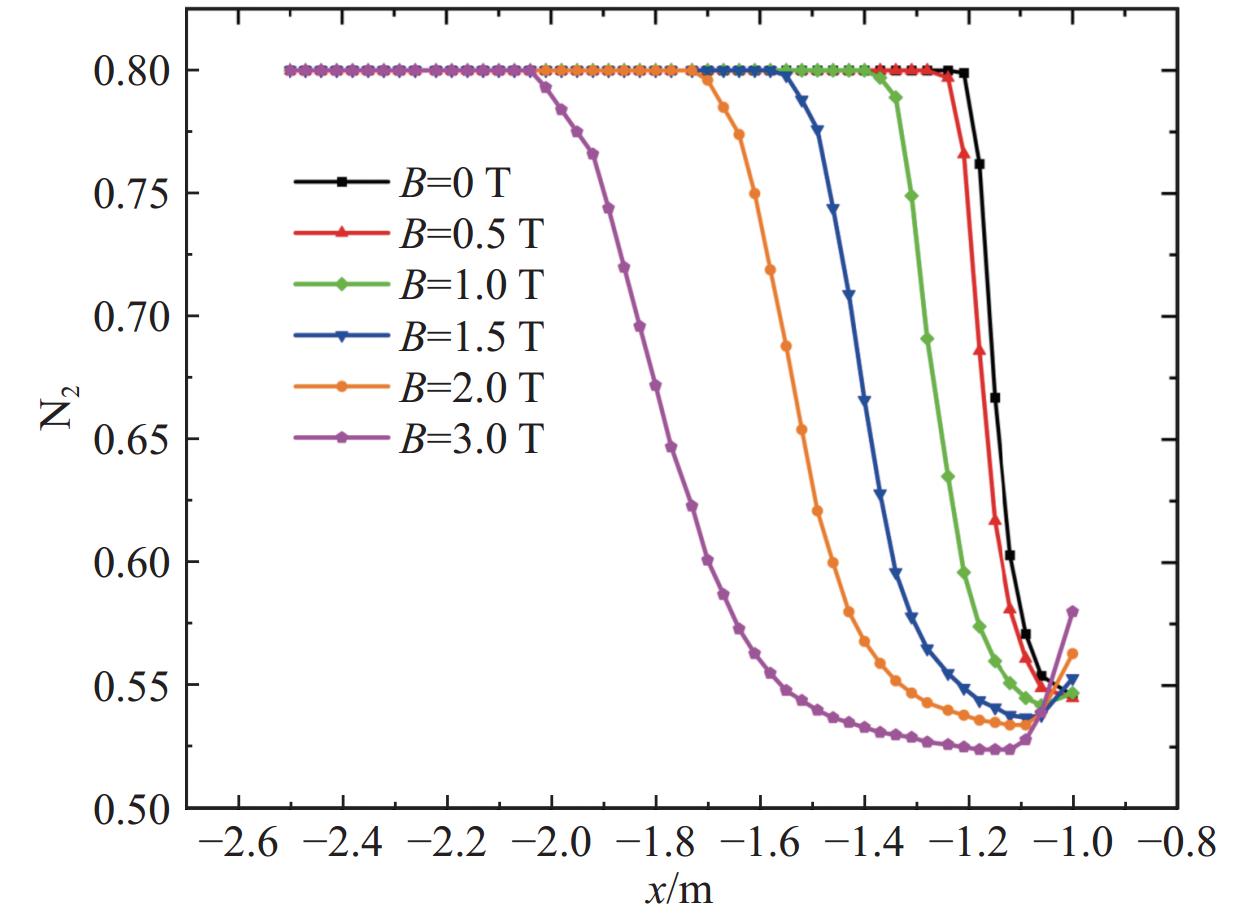
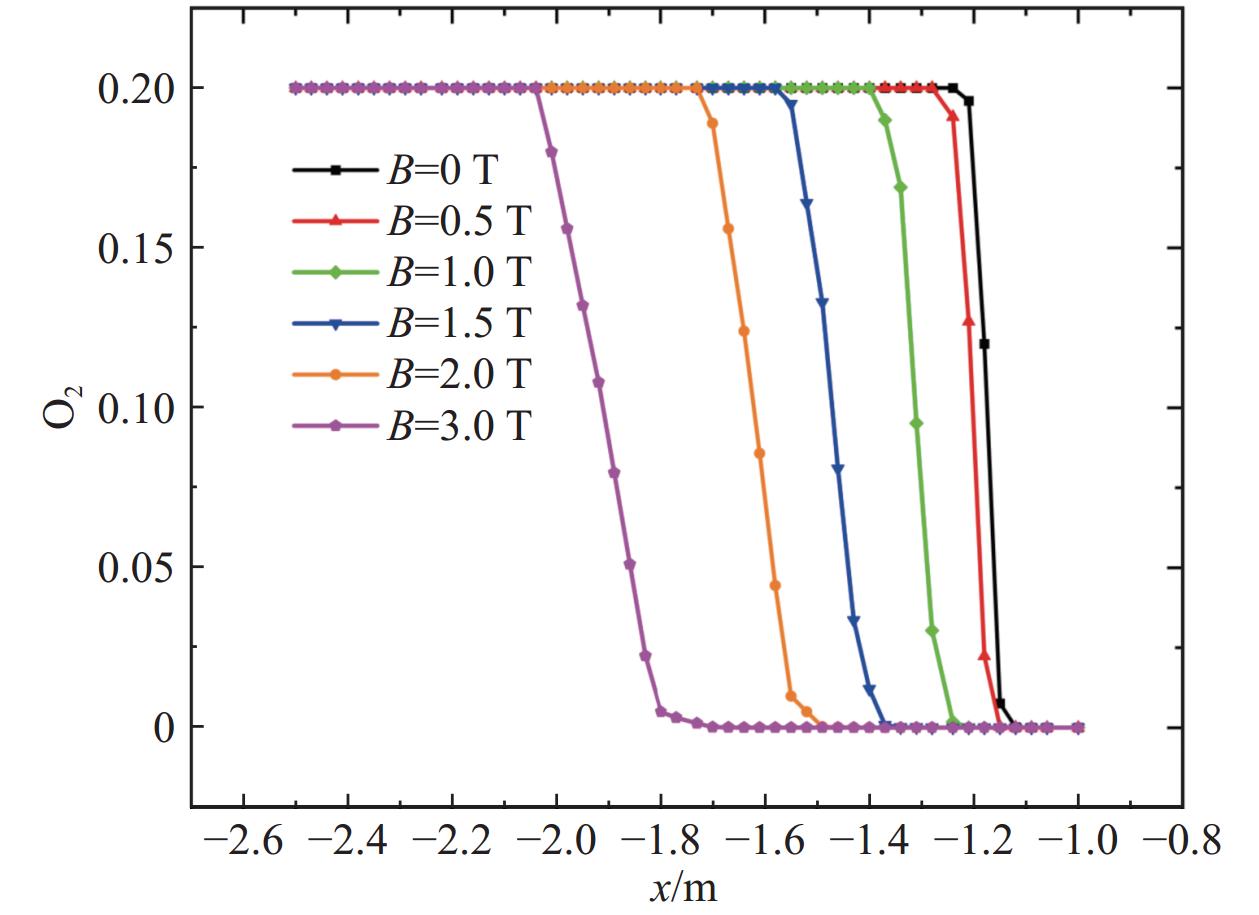
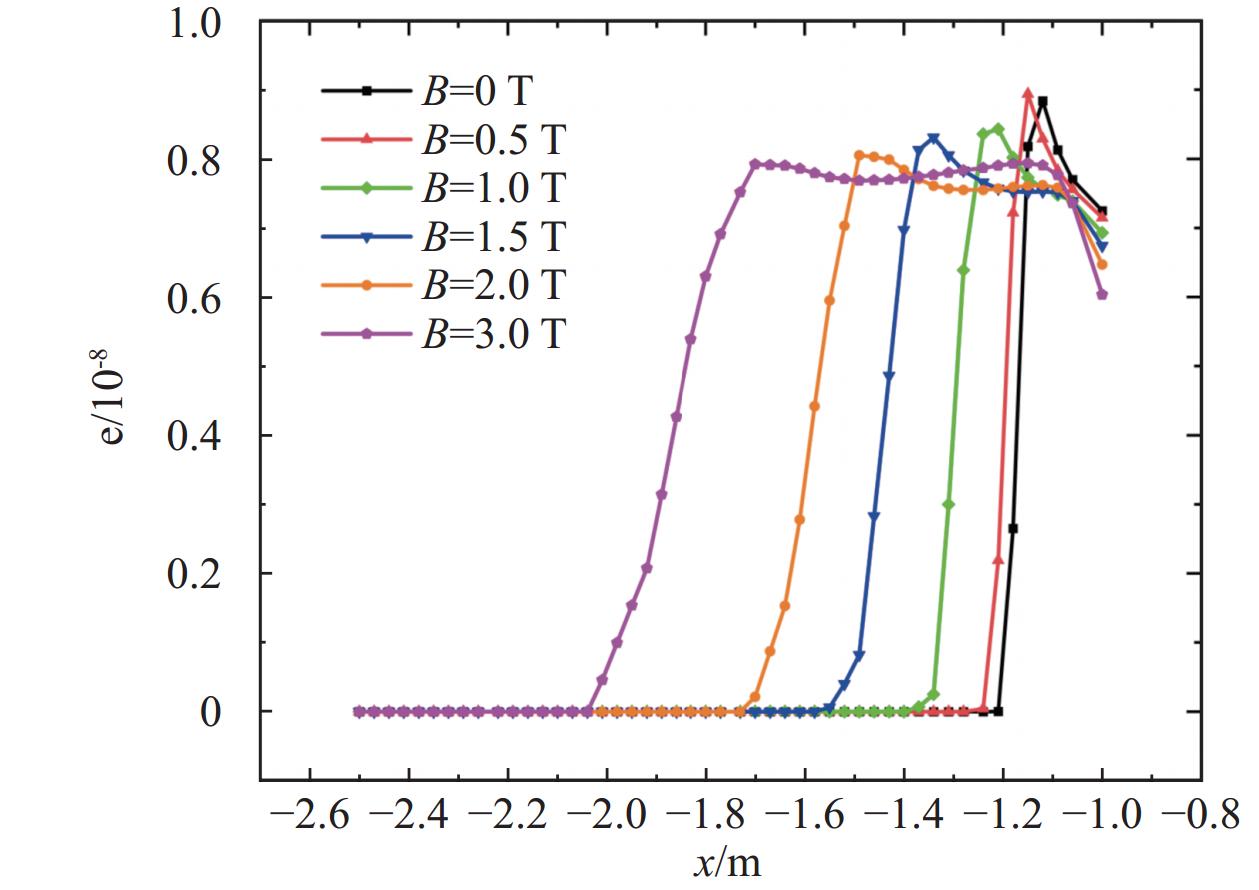
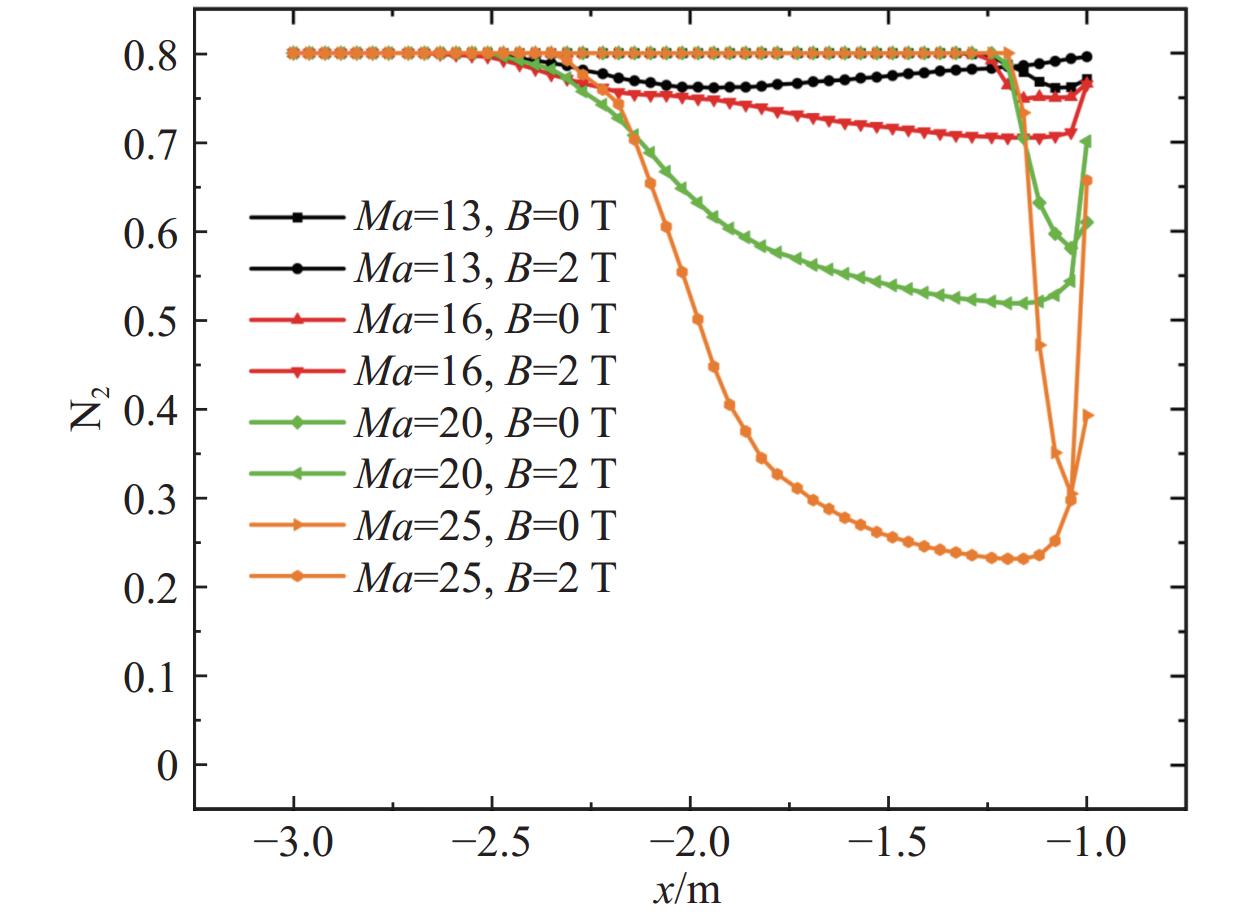
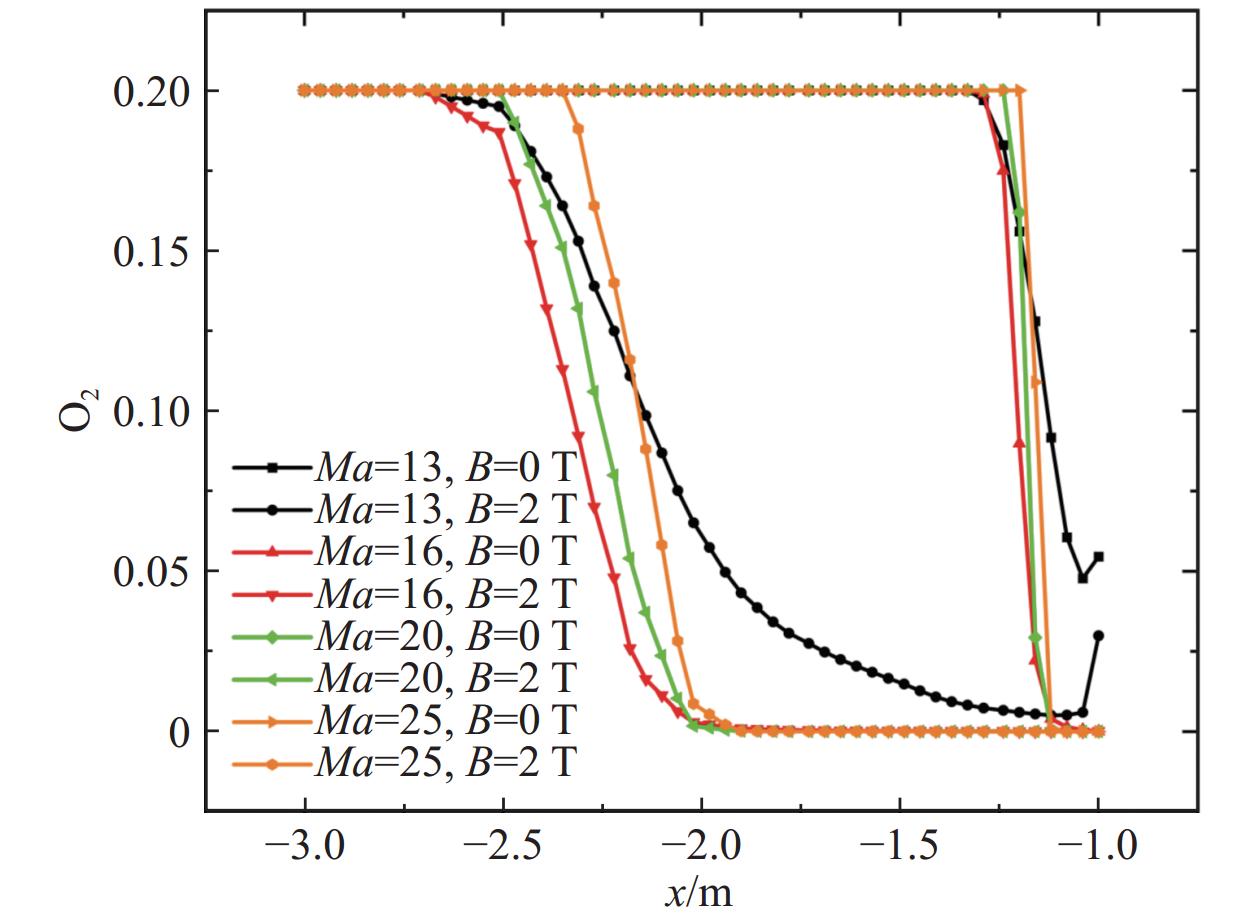
图 14 圆柱前缘滞止线平动温度和振动温度分布Figure 14. Translational temperature and vibration temperature distribution along the stagnation line of cylindrical leading edge图15和图16分别给出了不同磁感应强度下的圆柱前缘滞止线N2和O2摩尔分数分布。可以看到磁感应强度越大，N2和O2离解反应发生得越早，这是由于随着磁感应强度的增大，弓形激波前移，气流经过弓形激波后，温度急剧升高，当温度达到N2和O2的离解温度时，两种组分摩尔分数开始下降，生成N原子和O原子。值得注意的是，由图15可以看出，N2离解程度受磁场影响比较明显：磁感应强度越大，N2浓度最小值越小，B0 = 0 T时N2最低浓度为0.55，当B0 =3 T时降至0.52；当N2浓度达到最小时，在壁面附近又发生复合反应，导致N2浓度有短暂回升，且回升幅度随磁感应强度增强而增大。相比之下，O2离解程度基本不受磁场影响，这是由于O2离解温度较低，而弓形激波后温度较高，因此在到达壁面之前就已完全离解。图17给出了不同磁感应强度下的圆柱前缘滞止线电子摩尔分数分布。由图可以看出，磁感应强度大小显著影响滞止线电子浓度的分布：磁感应强度越大，峰值位置离壁面越远，但峰值大小变化幅度相对较小。
![]()
图 15 圆柱前缘滞止线N2摩尔分数分布Figure 15. N2 mole fraction distribution along the stagnation line of cylindrical leading edge![]()
图 16 圆柱前缘滞止线O2摩尔分数分布Figure 16. O2 mole fraction distribution along the stagnation line of cylindrical leading edge![]()
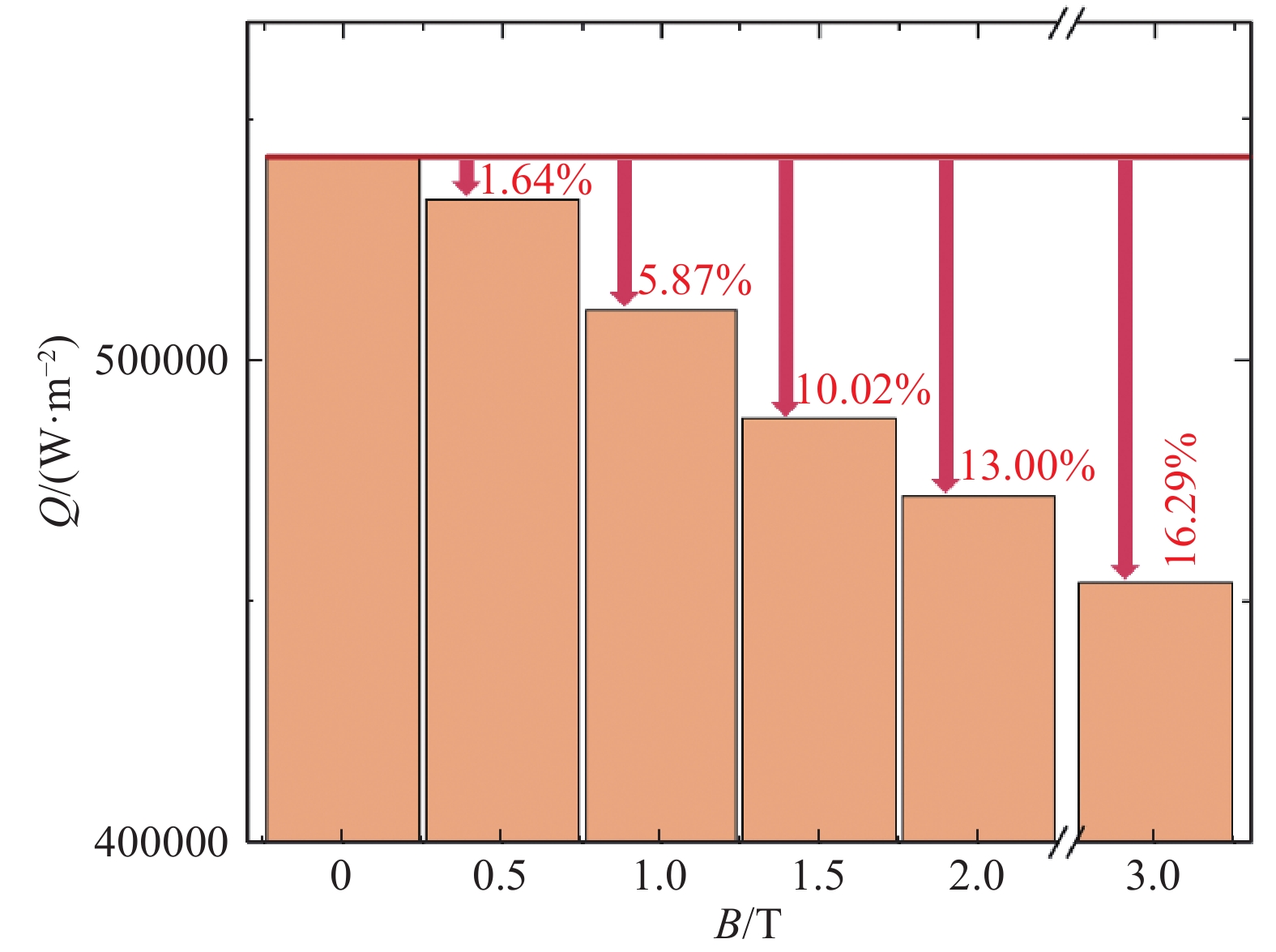
图 17 圆柱前缘滞止线电子摩尔分数分布Figure 17. Electron mole fraction distribution along the stagnation line of cylindrical leading edge图18为不同磁感应强度下的驻点热流柱状图。可以看到，磁场对驻点热流影响显著，随着磁感应强度增大，驻点热流降低幅度不断增大：当B = 1 T时，驻点热流降低了5.87%，B = 3 T时，降幅达16.29%。这是由于随着磁感应强度的增大，激波脱体距离增大，温度峰值远离壁面，减小了壁面温差，导致热流幅值下降，可以对再入飞行器起到很好的热防护作用。
![]()
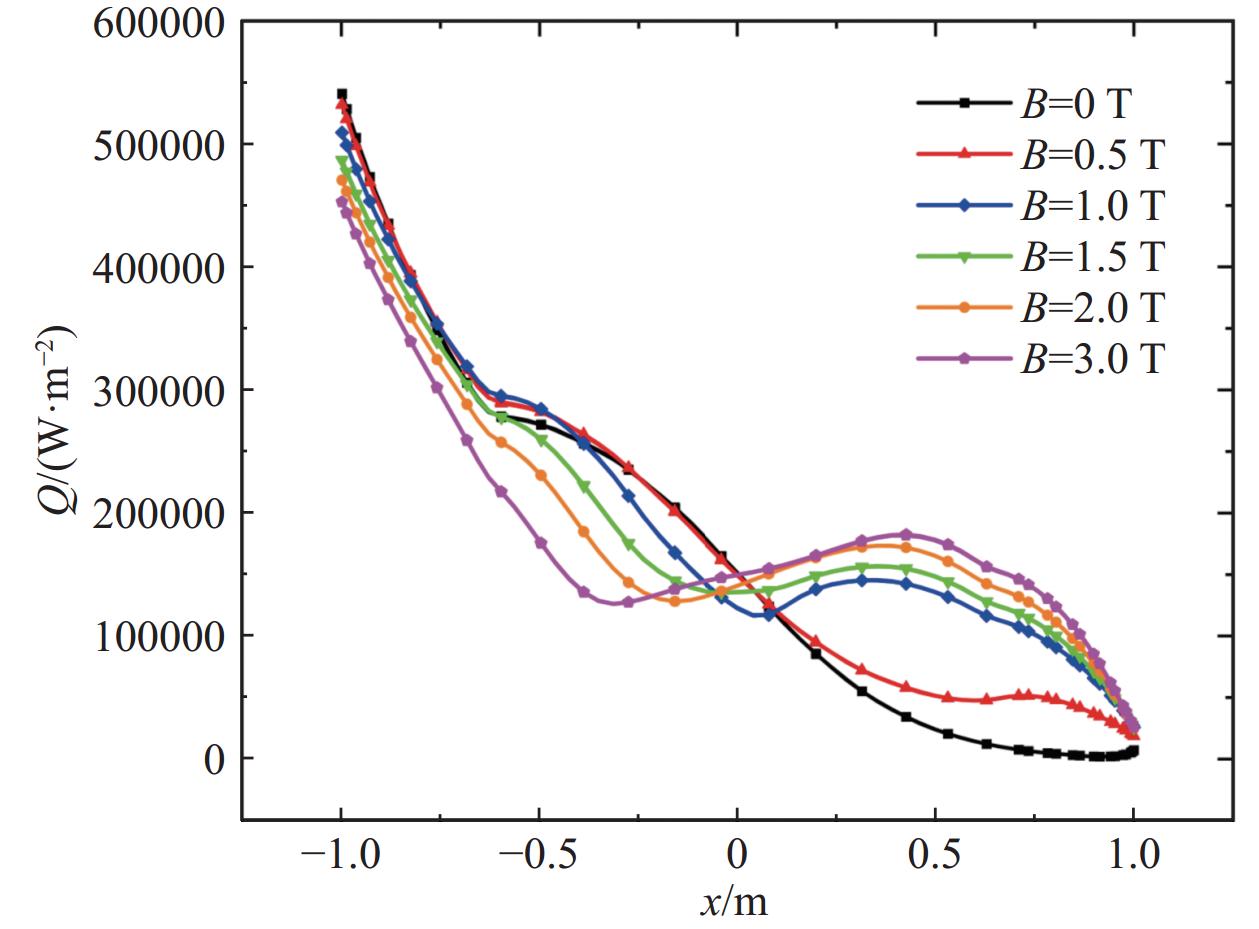
图 18 不同磁感应强度下的驻点热流柱状图Figure 18. Bar chart of stagnation point heat flux under different magnetic induction intensities图19给出了不同磁感应强度下的圆柱表面热流变化曲线。在圆柱前缘部分，随着磁感应强度的增大，壁面热流有所下降，而在圆柱两侧以及后方，磁场越强，壁面热流越大，结合图11洛伦兹力矢量图可以发现，在圆柱两侧附近，洛伦兹力方向指向圆柱壁面，进而导致两侧气流速度增加，滞止摩擦产生的温度升高，与壁面温差增大，热流增大。这也就是所谓的“肩部过热”现象，可见并不能一味的增大磁感应强度来降低前缘气动热，同时还要考虑肩部热负荷以及磁体系统的重量和复杂性。
![]()
图 19 不同磁感应强度下圆柱壁面热流变化Figure 19. Surface heat flux of the cylinder under different magnetic induction intensities2.2 不同马赫数下磁场对热化学非平衡流动的影响
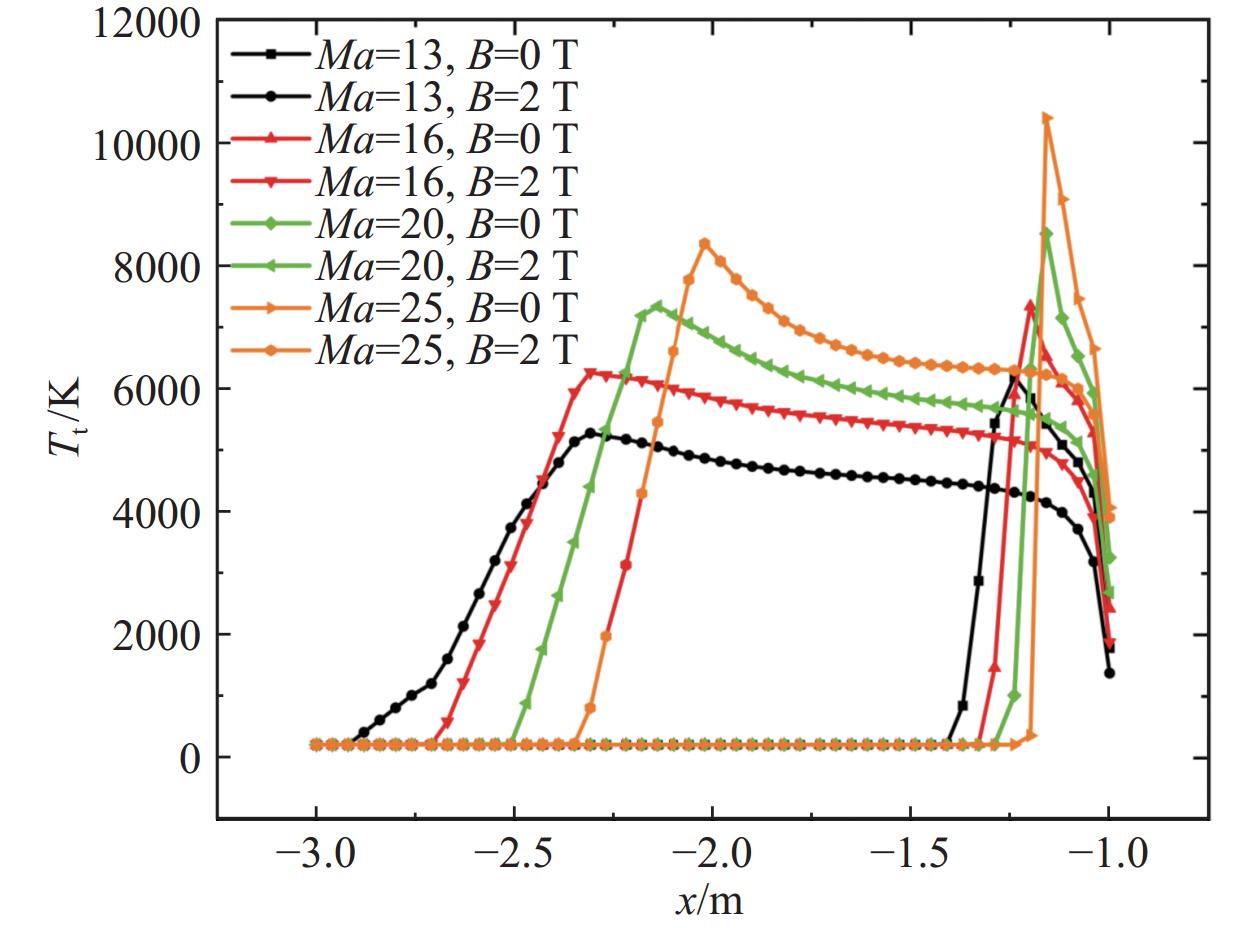
图20给出了马赫数13～25下的滞止线平动温度分布曲线。可以看出，当磁场为0 T时，随着马赫数的增大，激波位置逐渐向壁面靠近，同时峰值温度升高。而当配置偶极子磁场后，激波位置前移，同时相对于无磁场情形，相同马赫数下的峰值温度有所下降。Ma = 13时，加入磁场后峰值温度下降了14.74%，而当Ma = 25时，峰值温度下降了19.18%。
![]()
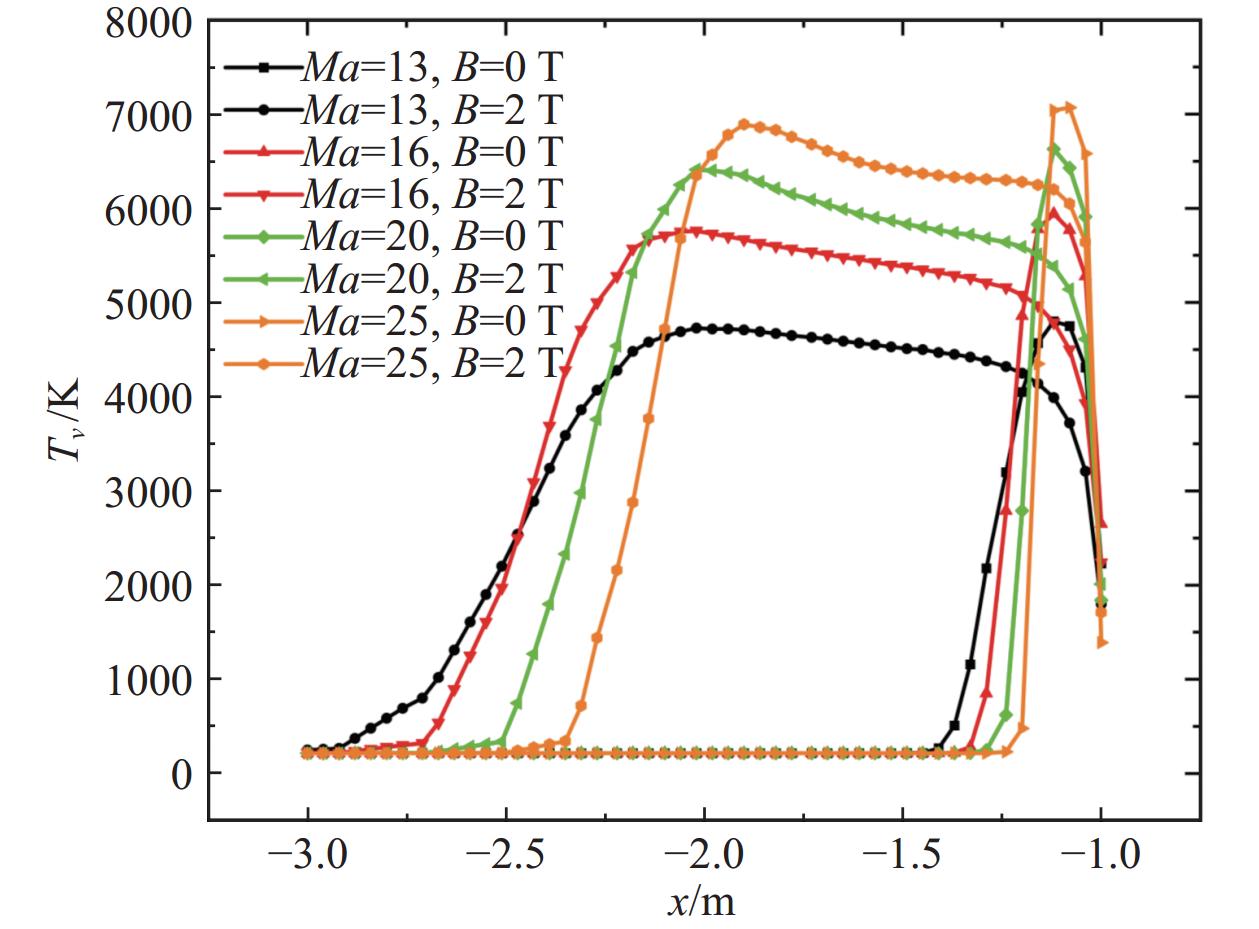
图 20 不同马赫数下磁场对滞止线平动温度分布的影响（H = 70 km）Figure 20. Effect of magnetic field on translational temperature distribution along stagnation line at different Mach numbers (H = 70 km)图21给出了各个工况下的滞止线振动温度分布曲线，磁场的存在对振动温度的影响主要体现在激波前移，振动温度提前上升，但是振动温度峰值仅有略微下降。当磁场为0 T时，振动温度峰值几乎在同一位置，然而当加入磁场后，随着马赫数的增大，不同马赫数下的振动温度峰值位置有所不同，马赫数越大，振动温度峰值位置越靠近壁面。由温度分布可见，磁场对大马赫数的影响较为显著，主要体现在平动温度峰值下降以及两种温度峰值位置变化。
![]()
图 21 不同马赫数下磁场对滞止线振动温度分布的影响（H = 70 km）Figure 21. Effect of magnetic field on vibration temperature distribution along stagnation line at different Mach numbers (H = 70 km)图22和23分别给出了各个工况下的滞止线N2和O2摩尔分数分布曲线，当磁场为0 T时，N2和O2的离解程度随着马赫数的升高而增大，当Ma达到16时，O2已经完全离解，而N2仅仅离解了6.40%。随着马赫数的继续升高，N2的离解程度不断增大，当Ma = 25时，N2离解程度达到了61.8%。当对Ma = 13时的工况加入磁场后，相对于无磁场 N2波后浓度最小值变化不大，但是在近壁面又发生了N2的复合反应，导致N2浓度升高；而O2离解程度在加入磁场后变化较为明显，最小值下降了89.32%。随着马赫数的继续升高，N2离解程度逐渐增大，在壁面附近复合反应生成的N2浓度也越高。而O2由于已经完全离解，仅仅是开始离解位置前移。
![]()
图 22 不同马赫数下滞止线N2摩尔分数分布曲线（H = 70 km）Figure 22. N2 mole fraction distribution at the stagnation line under each working condition (H = 70 km)![]()
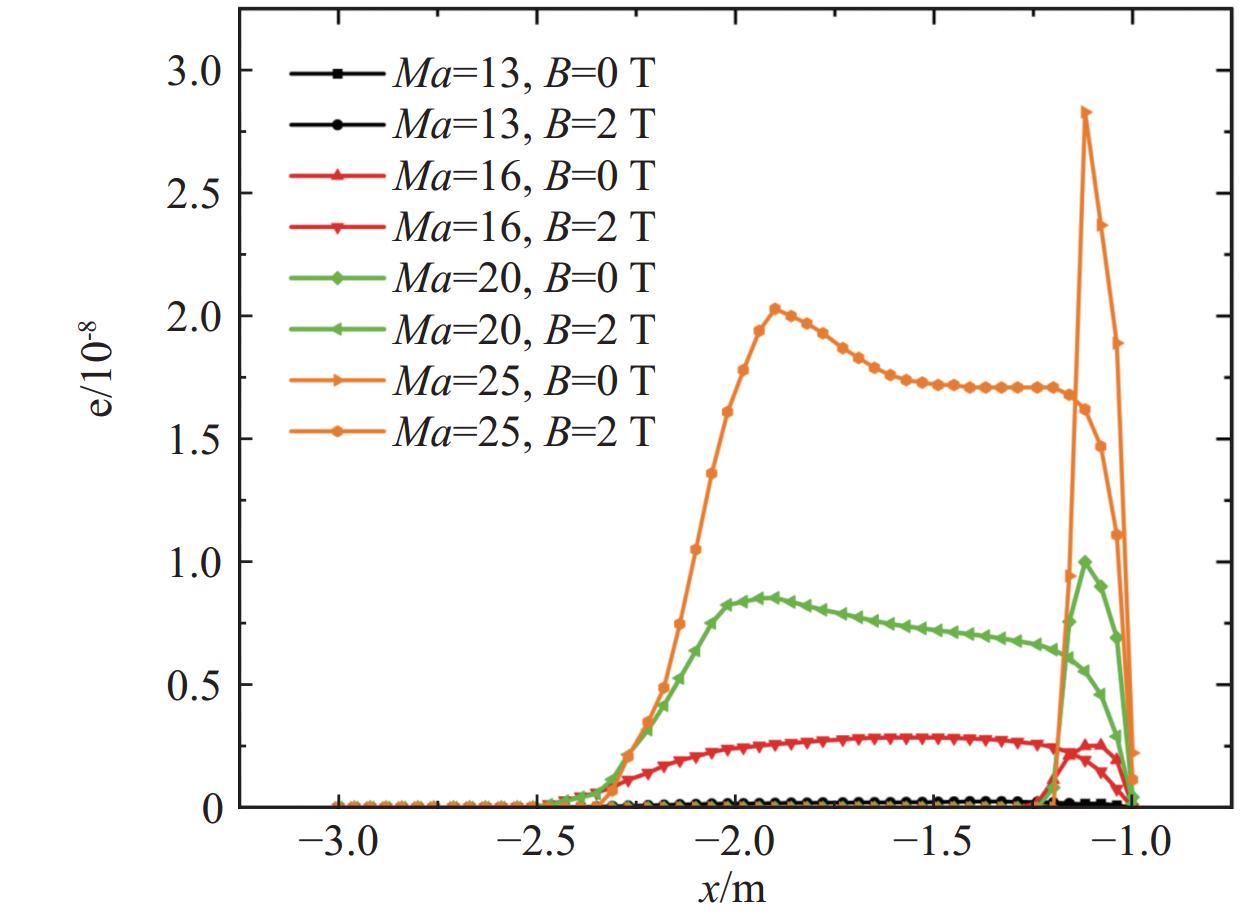
图 23 不同马赫数下滞止线O2摩尔分数分布（H = 70 km）Figure 23. O2 mole fraction distribution along the stagnation line at deferent Mach numbers (H = 70 km)图24给出了各个工况下的滞止线电子浓度分布曲线，可以看出，Ma = 13时，由于来流气体动能较低，经过激波压缩后产生的温度较低，此时气体电离程度较低，电子浓度无显著变化。随着马赫数不断升高，来流气体动能增大，进而导致波后温度升高，气体电离程度增大，导致电子浓度升高。同时磁场对高马赫数工况电子浓度峰值影响较大， Ma = 25时，加入磁场后电子浓度相比于无磁场下降了28.44%。
![]()
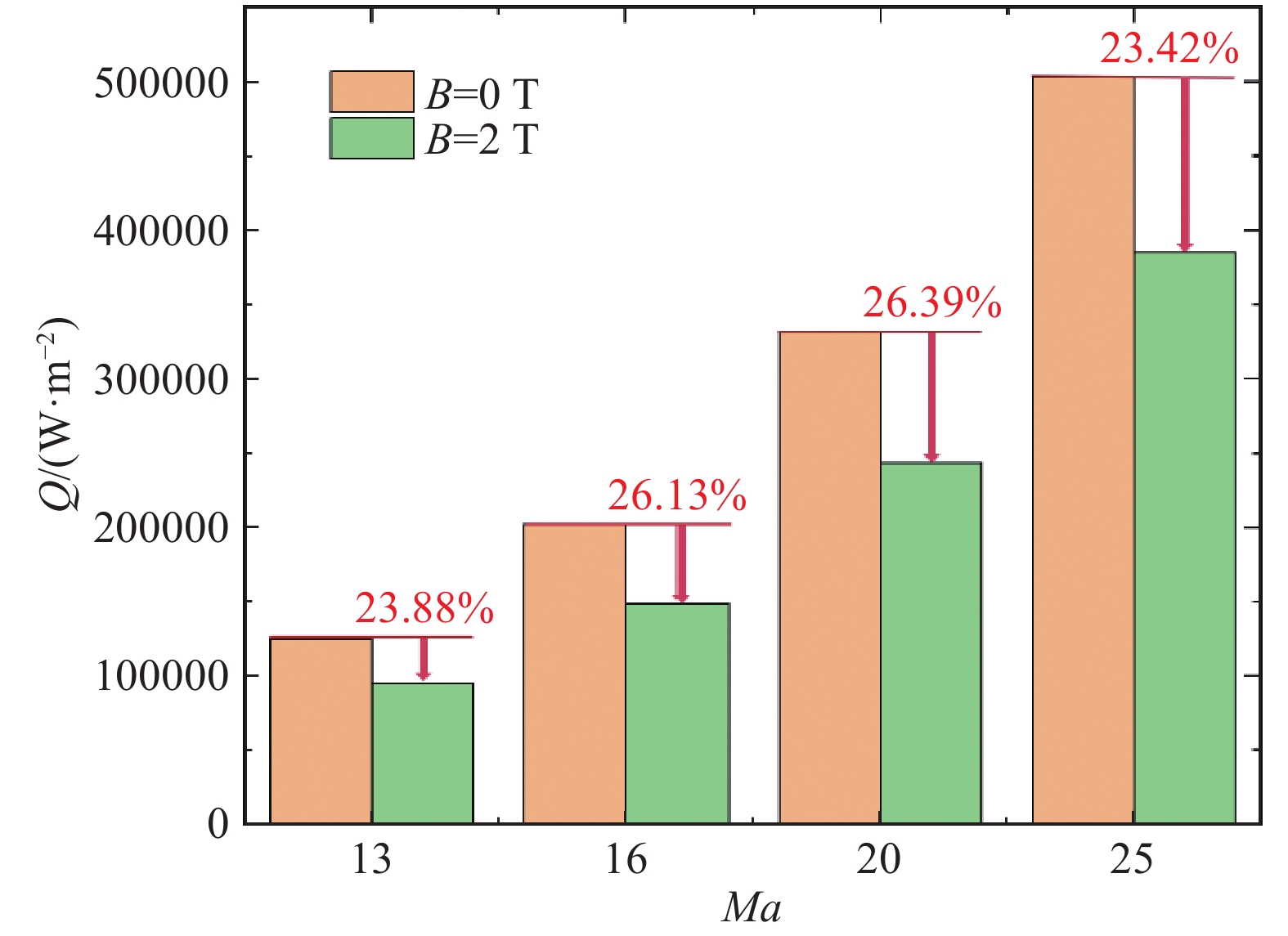
图 24 不同马赫数下滞止线电子摩尔分数分布（H = 70 km）Figure 24. Electron mole fraction distribution along the stagnation line at deferent Mach numbers (H = 70 km)图24给出了不同马赫数加入磁场后驻点热流变化图。当无磁场时，随着马赫数的升高，驻点热流逐渐增大，这是由于来流气体动能逐渐增大，导致激波后温度增大，进而增大了气体与壁面的温差，导致热流增大。加入磁场后，由于激波前移，波后温度峰值前移，导致近壁面处温度降低，进而导致热流降低。由图25可以看出，随着马赫数的增大，驻点热流降低绝对值越来越大，但是降低比例变化不明显，降低比例受马赫数影响较小。
![]()
图 25 不同马赫数下磁场对驻点热流的影响（H = 70 km）Figure 25. Effect of magnetic field on stagnation heat flux at different Mach numbers (H = 70 km)2.3 相同配置磁场对不同高度下的热化学非平衡流动影响
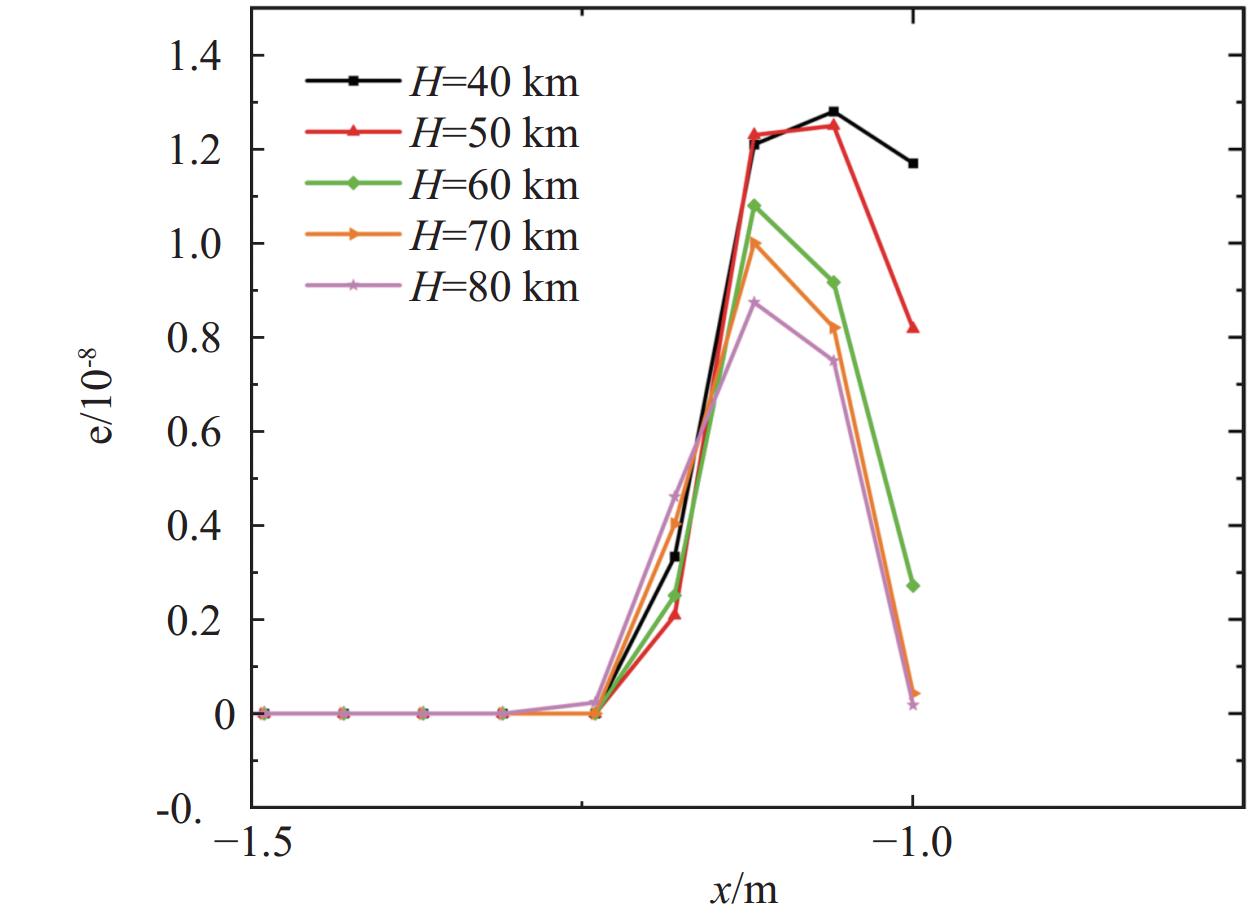
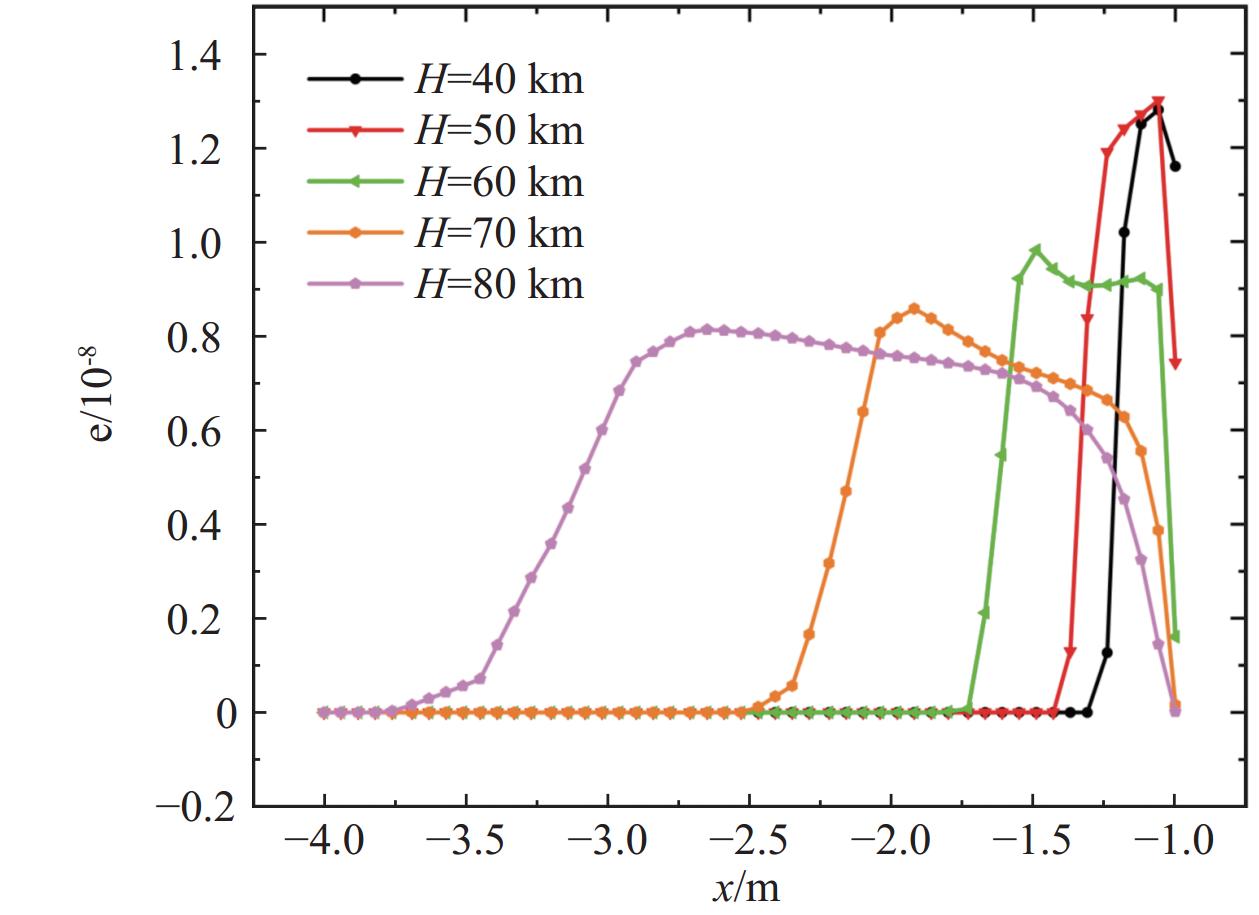
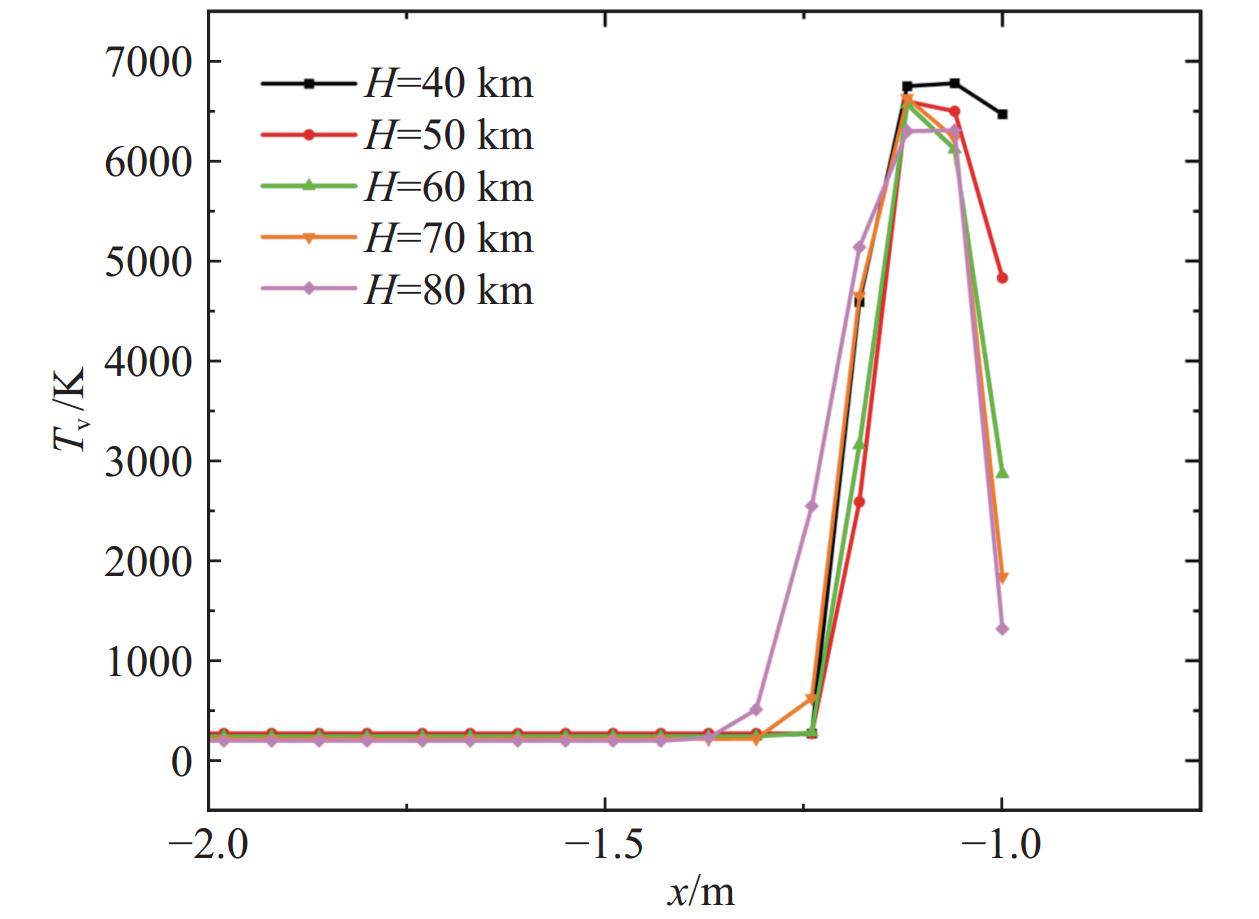
图26给出了B0 = 0 T时不同高度滞止线电子摩尔分数分布曲线。可以看出，在马赫数相同且不加入磁场时，激波位置受高度影响较小，且电子浓度达到峰值的位置也几乎不变。但是随着高度的增加，电子浓度峰值却在降低，这是由于高度越低，分子数密度越高，导致气体经过激波压缩后温度剧烈升高，达到电离温度后开始电离并生成电子，且高度越低，电离程度越大，因此电子浓度峰值也越大。图27给出了B0 = 2 T时不同高度滞止线电子摩尔分数分布曲线。同一高度下，磁场的加入会导致激波位置显著前移，电子浓度峰值略微下降，且高度越高，激波位置前移距离越大。
![]()
图 26 不同高度下滞止线电子摩尔分数分布（B0 = 0 T, Ma = 20）Figure 26. Electron molar concentration distribution along the stagnation line at different altitudes under B0 = 0 T, Ma = 20![]()
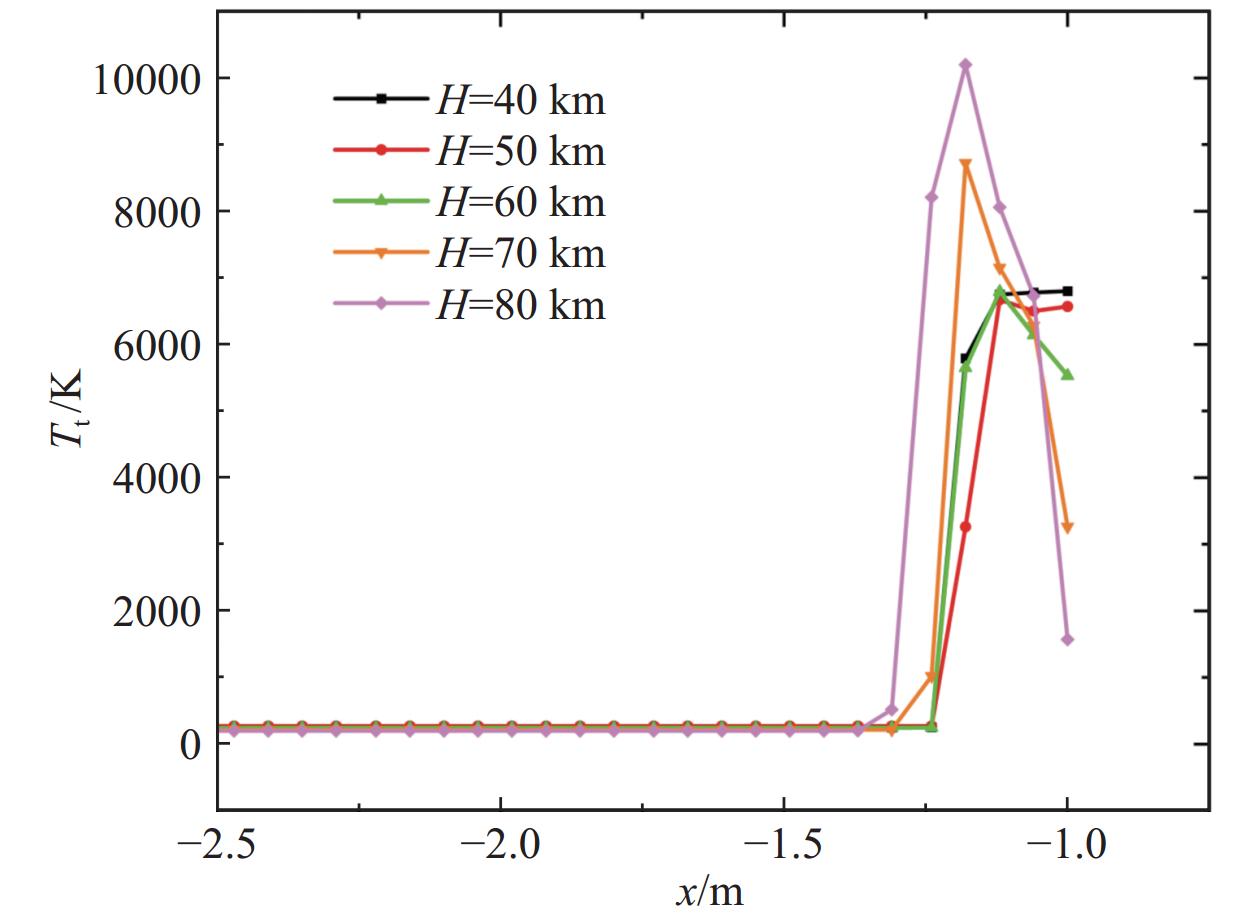
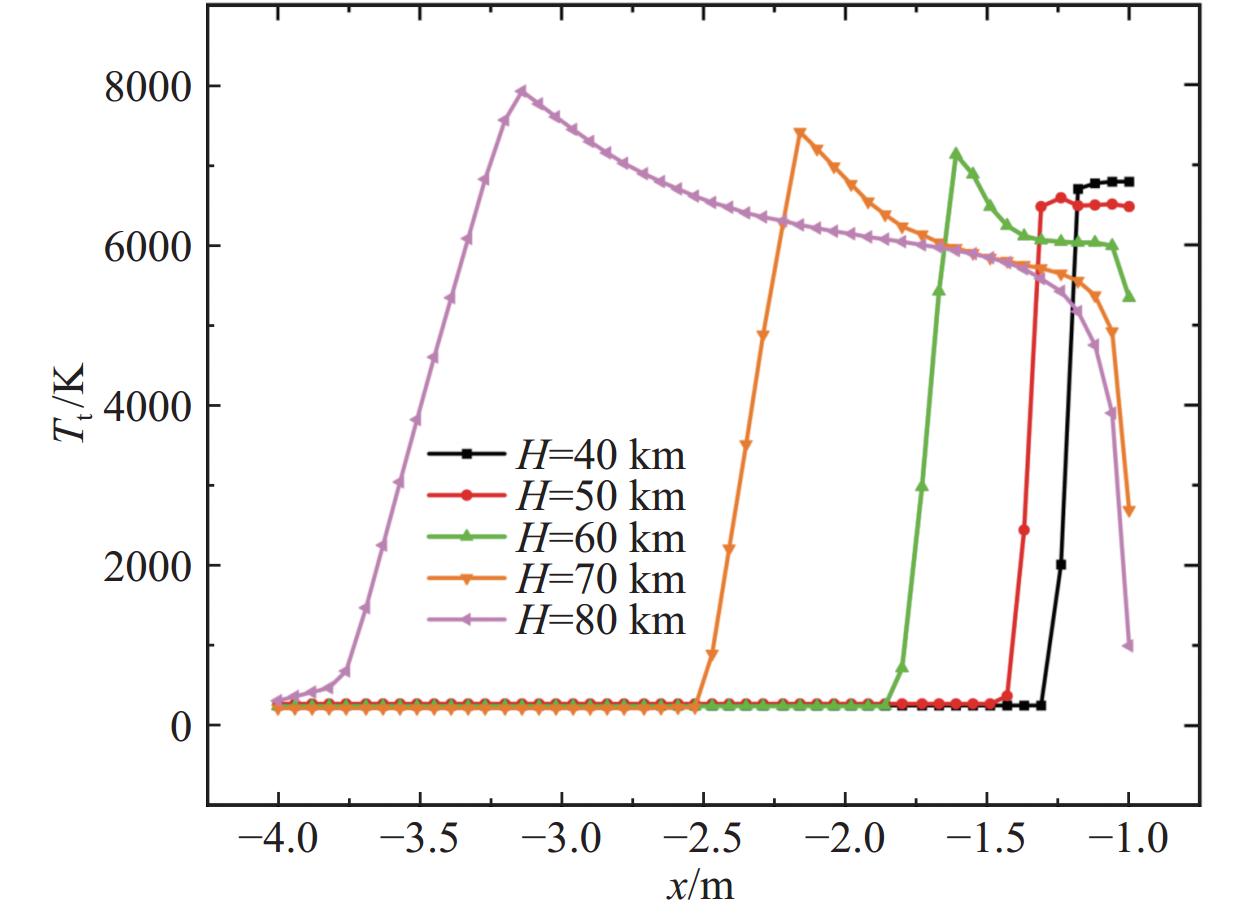
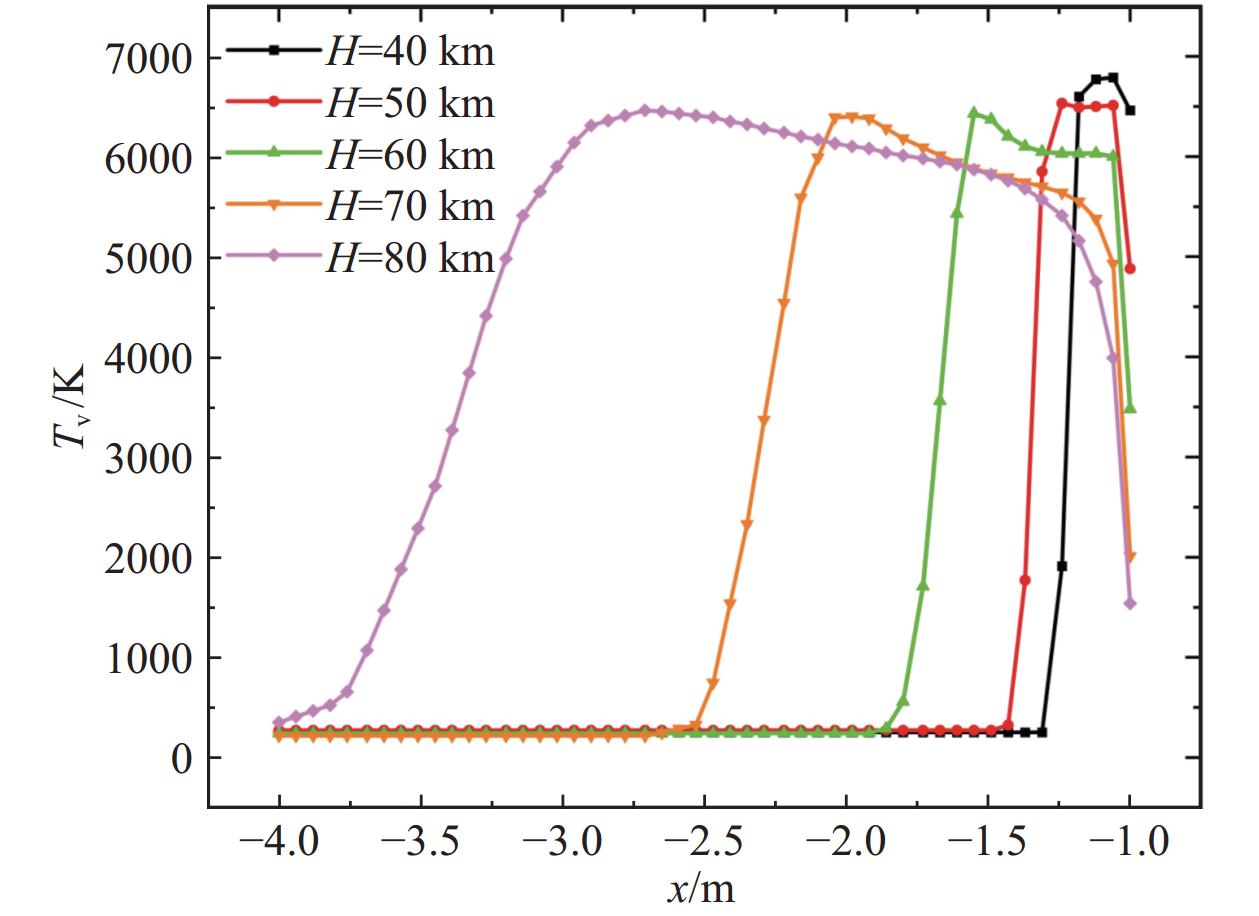
图 27 不同高度下滞止线电子摩尔分数分布（B0 = 2 T、Ma = 20）Figure 27. Electron molar concentration distribution along stagnation line at different altitudes under B0 = 2 T, Ma = 20图28给出了B0 = 0 T时不同高度滞止线平动温度分布曲线，可以看出，当磁场为0 T时，随着高度的增加平动温度峰值逐渐升高，这是由于当高度较低时，分子数密度较大，电离程度也越大，而电离反应会吸收部分热量，导致平动温度较低。随着高度的增加，电离程度降低，平动温度逐渐升高。而在近壁面处，高度越高，平动温度反而越低。这是由于高度较低时，由于各粒子数密度较高，碰撞频繁，发生了大量的复合反应，导致电子浓度下降，同时放出大量热量，温度升高。图29给出了B0 = 2 T时不同高度滞止线平动温度分布曲线。可以看到，加入磁场后，平动温度峰值降低，且位置前移，高度越高，磁场的作用越明显。
![]()
图 28 不同高度下滞止线平动温度分布曲线（B0 = 0 T, Ma = 20）Figure 28. Translational temperature distribution along the stagnation line at different altitudes under B0 = 0 T, Ma = 20![]()
图 29 不同高度下滞止线平动温度分布（B0 = 2 T, Ma = 20）Figure 29. Translational temperature distribution along the stagnation line at different altitudes under B0 = 2 T, Ma = 20图30给出了B0 = 0 T时不同高度滞止线振动温度分布曲线。可以看出加入磁场前不同高度下的振动温度分布差异不大，振动温度峰值随着高度的增加有略微的降低，这是由于高度较低时，分子数密度较大，平动温度的剧烈升高导致振动能被充分激发，进而吸收部分平动能，并开始发生电离，且电离程度较高，这也是高度越低，平动温度相对较低的原因。图31给出了B0 = 2 T时不同高度滞止线振动温度分布曲线。当加入磁场后，振动温度峰值大小变化不明显，但是达到峰值的位置前移，且高度越高，前移距离越大。
![]()
图 30 不同高度下滞止线振动温度分布（B0 = 0 T, Ma = 20）Figure 30. Vibration temperature distribution along with stagnation line at different altitudes under B0 = 0 T, Ma = 20![]()
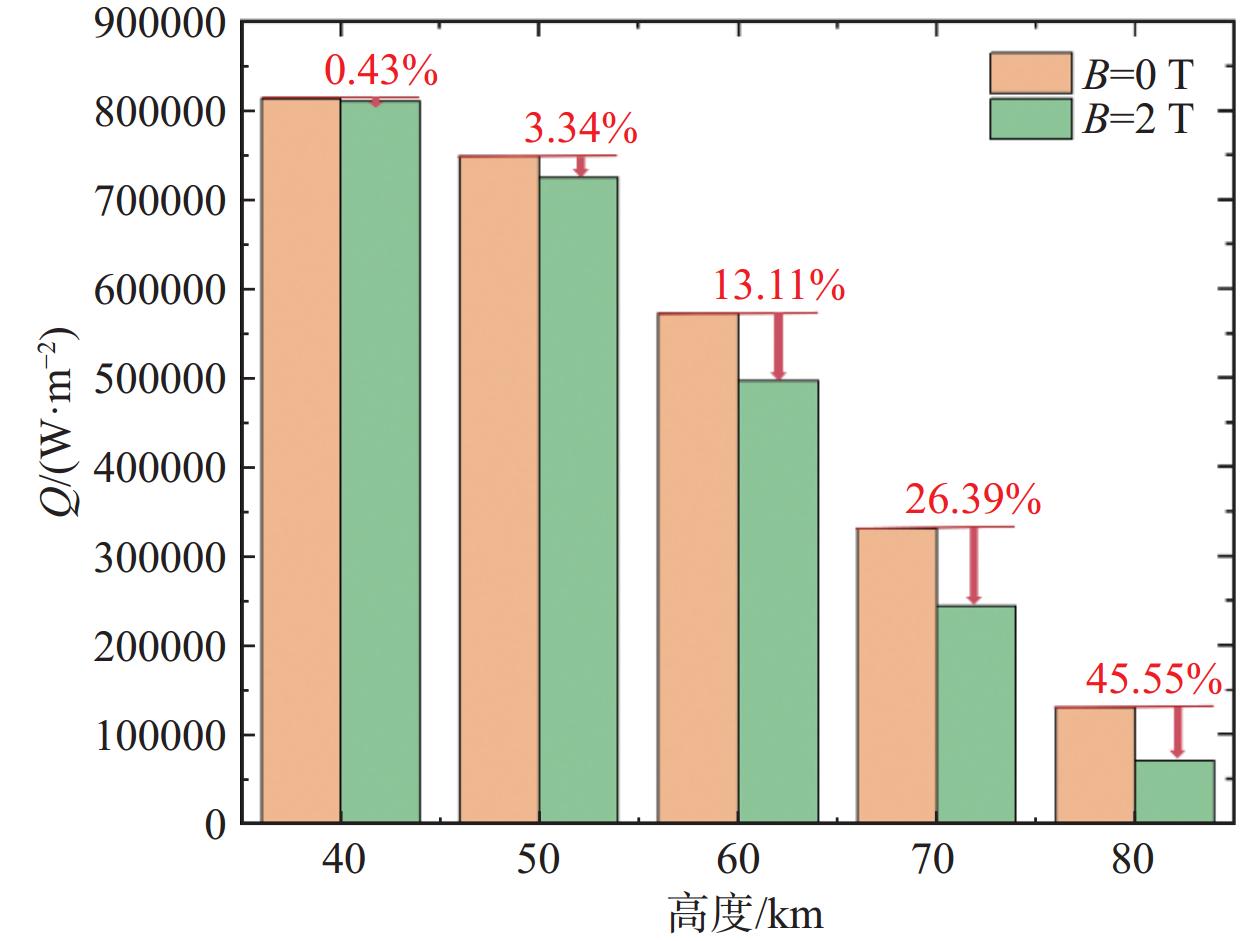
图 31 不同高度下滞止线振动温度分布（B0 = 2 T, Ma = 20）Figure 31. Vibration temperature distribution along the stagnation line at different altitudes under B0 = 2 T, Ma = 20图32给出了不同高度条件加入磁场后驻点热流变化图。当无磁场时，随着高度的升高，驻点热流逐渐降低，这是由于高度越高，壁面附近气体温度越低，与壁面的温差减小，进而热流降低。当加入磁场后，同一高度下的驻点热流均有所下降，这是由于加入磁场后，壁面处气体平动温度显著下降，导致温差减小；且随着高度的增加，驻点热流下降幅度增大，当H = 40 km时热流仅下降了0.43%，而H = 80 km时，热流下降幅度达到了45.55%，因此磁控热防护仅在高度较高时效果才会明显。
![]()
图 32 不同高度下磁场对驻点热流的影响（Ma = 20）Figure 32. Effect of magnetic field on stagnation heat flux at different altitudes (Ma = 20)3. 结 论
本文针对高速磁流体热化学非平衡流动问题，通过耦合NCCR方程和Maxwell电磁场控制方程，建立了低磁雷诺数高速磁流体热化学非平衡数值模拟方法及程序，通过高速等离子体圆柱扰流算例验证了本文磁流体数值模拟方法能够较准确地模拟高速稀薄等离子体流动，并得到以下结论：
1） 对于圆柱扰流，磁场的存在将会显著影响高速等离子体流场结构，激波脱体距离显著增大。在本文研究条件下，当B0 = 3 T时，激波脱体距离比无磁场时增加了452.38%。
2） 随着磁感应强度的增大，气体与壁面温差减小，驻点热流显著下降，下降幅度受磁感应强度大小、来流高度、来流马赫数影响。磁感应强度和来流马赫数越大、高度越高，磁控热防护效果越显著，当H = 80 km时，驻点热流下降幅度达到了45.55%。
3） 高速磁流体热化学非平衡效应受磁场影响较为显著，主要体现在波后N2的离解程度以及近壁面附近的N2复合反应，随着磁场的增强，波后N2浓度最小值降低，而由于壁面附近电子受洛伦兹力影响向滞止线附近运动，导致近壁面复合反应发生更易发生，因此近壁面N2浓度较高，电子浓度较低。
目前本研究尚未考虑霍尔效应的影响，在高空强磁场的条件下，霍尔效应不可忽略，这将是下一步工作的开展方向。
-
![]()
图 32 不同高度下磁场对驻点热流的影响（Ma = 20）
Figure 32. Effect of magnetic field on stagnation heat flux at different altitudes (Ma = 20)
![]()
图 3 OREX返回舱周围磁场分布
Figure 3. Distribution of the magnetic field around the OREX re-entry capsule
![]()
图 4 OREX返回舱壁面热流分布曲线
Figure 4. Wall heat flux distribution curve of OREX return capsule
![]()
图 5 磁场作用下的等离子体球体扰流示意图[8]
Figure 5. Schematic diagram of plasma sphere flow disturbance under magnetic field effects
![]()
图 6 不同网格数量壁面热流密度分布
Figure 6. Wall heat flux distribution curve on the wall with different grid
![]()
图 7 不同磁感应强度下的平动温度云图
Figure 7. Translational temperature contours with different magnetic induction intensities
![]()
图 8 不同磁感应强度下的振动温度云图
Figure 8. Vibration temperature contour with different magnetic induction intensities
![]()
图 9 不同磁感应强度下的压力云图
Figure 9. Pressure contours at different magnetic induction intensities
![]()
图 10 不同磁感应强度下的电子摩尔分数云图
Figure 10. Electron mole fraction contour with different magnetic induction intensities
![]()
图 11 不同磁感应强度下的洛伦兹力分布云图
Figure 11. Lorentz force distribution contour with different magnetic induction intensities
![]()
图 13 不同磁感应强度下的电流密度分布云图
Figure 13. Contour of current density distribution with different magnetic induction intensities
![]()
图 14 圆柱前缘滞止线平动温度和振动温度分布
Figure 14. Translational temperature and vibration temperature distribution along the stagnation line of cylindrical leading edge
![]()
图 15 圆柱前缘滞止线N2摩尔分数分布
Figure 15. N2 mole fraction distribution along the stagnation line of cylindrical leading edge
![]()
图 16 圆柱前缘滞止线O2摩尔分数分布
Figure 16. O2 mole fraction distribution along the stagnation line of cylindrical leading edge
![]()
图 17 圆柱前缘滞止线电子摩尔分数分布
Figure 17. Electron mole fraction distribution along the stagnation line of cylindrical leading edge
![]()
图 18 不同磁感应强度下的驻点热流柱状图
Figure 18. Bar chart of stagnation point heat flux under different magnetic induction intensities
![]()
图 19 不同磁感应强度下圆柱壁面热流变化
Figure 19. Surface heat flux of the cylinder under different magnetic induction intensities
![]()
图 20 不同马赫数下磁场对滞止线平动温度分布的影响（H = 70 km）
Figure 20. Effect of magnetic field on translational temperature distribution along stagnation line at different Mach numbers (H = 70 km)
![]()
图 21 不同马赫数下磁场对滞止线振动温度分布的影响（H = 70 km）
Figure 21. Effect of magnetic field on vibration temperature distribution along stagnation line at different Mach numbers (H = 70 km)
![]()
图 22 不同马赫数下滞止线N2摩尔分数分布曲线（H = 70 km）
Figure 22. N2 mole fraction distribution at the stagnation line under each working condition (H = 70 km)
![]()
图 23 不同马赫数下滞止线O2摩尔分数分布（H = 70 km）
Figure 23. O2 mole fraction distribution along the stagnation line at deferent Mach numbers (H = 70 km)
![]()
图 24 不同马赫数下滞止线电子摩尔分数分布（H = 70 km）
Figure 24. Electron mole fraction distribution along the stagnation line at deferent Mach numbers (H = 70 km)
![]()
图 25 不同马赫数下磁场对驻点热流的影响（H = 70 km）
Figure 25. Effect of magnetic field on stagnation heat flux at different Mach numbers (H = 70 km)
![]()
图 26 不同高度下滞止线电子摩尔分数分布（B0 = 0 T, Ma = 20）
Figure 26. Electron molar concentration distribution along the stagnation line at different altitudes under B0 = 0 T, Ma = 20
![]()
图 27 不同高度下滞止线电子摩尔分数分布（B0 = 2 T、Ma = 20）
Figure 27. Electron molar concentration distribution along stagnation line at different altitudes under B0 = 2 T, Ma = 20
![]()
图 28 不同高度下滞止线平动温度分布曲线（B0 = 0 T, Ma = 20）
Figure 28. Translational temperature distribution along the stagnation line at different altitudes under B0 = 0 T, Ma = 20
![]()
图 29 不同高度下滞止线平动温度分布（B0 = 2 T, Ma = 20）
Figure 29. Translational temperature distribution along the stagnation line at different altitudes under B0 = 2 T, Ma = 20
![]()
图 30 不同高度下滞止线振动温度分布（B0 = 0 T, Ma = 20）
Figure 30. Vibration temperature distribution along with stagnation line at different altitudes under B0 = 0 T, Ma = 20
-
[1] 丁明松, 江涛, 董维中, 等. 热化学模型对高超声速磁流体控制数值模拟影响分析[J]. 物理学报, 2019, 68(17): 182−194. doi: 10.7498/aps.68.20190378 DING M S, JIANG T, DONG W Z, et al. Numerical analysis of influence of thermochemical model on hypersonic magnetohydrodynamic control[J]. Acta Physica Sinica, 2019, 68(17): 182−194. (in Chinese) doi: 10.7498/aps.68.20190378
[2] FUJINO T, ISHIKAWA M. Numerical Simulation of control of plasma flow with magnetic field for thermal protection in Earth reentry flight[J]. IEEE Transactions on Plasma Science, 2006, 34(2): 409−420. doi: 10.1109/TPS.2006.872458
[3] 张向洪. 高超声速流场电磁干扰数值模拟研究[D]. 南京: 南京航空航天大学, 2013. ZHANG X H. Numerical simulation of electromagnetic interference in hypersonic flow field[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013. (in Chinese)
[4] 胡宁, 闫二艳, 郑强林, 等. 基于正交电磁场的等离子体电子密度控制[J]. 空气动力学学报, 2024, 42(4): 105−114. doi: 10.7638/kqdlxxb-2023.0171 HU N, YAN E Y, ZHENG Q L, et al. Plasma electronic density manipulation based on orthogonal electromagnetic field[J]. Acta Aerodynamica Sinica, 2024, 42(4): 105−114. (in Chinese) doi: 10.7638/kqdlxxb-2023.0171
[5] 杨明娟. 离子推进器羽流电磁特性的PIC/MCC模拟研究[D]. 成都: 电子科技大学, 2017. YANG M J. PIC/MCC simulation study on electromagnetic characteristics of ion thruster plume[D]. Chengdu: University of Electronic Science and Technology of China, 2017. (in Chinese)
[6] HARADA S, AUGUSTINUS J, HOFFMANN K, et al. Development of a modified Runge-Kutta scheme with TVD limiters for the ideal 1-D MHD equations[C]// 13th Computational Fluid Dynamics Conference, Snowmass Village, CO, USA. AIAA, 1997: AIAA1997-2090. doi: 10.2514/6.1997-2090
[7] BRIO M, WU C C. An upwind differencing scheme for the equations of ideal magnetohydrodynamics[J]. Journal of Computational Physics, 1988, 75(2): 400−422. doi: 10.1016/0021-9991(88)90120-9
[8] LEFEVRE A, GILDFIND D E, GOLLAN R J, et al. Expansion tube experiments of magnetohydrodynamic aerobraking for superorbital earth reentry[J]. AIAA Journal, 2021: 1-13. doi: 10.2514/1.j060253
[9] 丁明松, 江涛, 刘庆宗, 等. 电导率模拟对高超声速MHD控制影响[J]. 航空学报, 2019, 40(11): 123009. DING M S, JIANG T, LIU Q Z, et al. Impact of simulation of electrical conductivity on hypersonic MHD control[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(11): 123009. (in Chinese)
[10] 罗凯, 汪球, 李进平, 等. 基于高温真实气体效应的双锥磁流体流动控制[J]. 航空学报, 2022, 43(S2): 79-91. LUO K, WANG Q, LI J P, et al. Magnetohydrodynamic flow control of double-cone under high temperature real gas effect [J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(S2): 76-88(in Chinese).
[11] 徐帅. 热化学非平衡流动磁流体力学控制数值模拟研究[D]. 哈尔滨: 哈尔滨工业大学, 2021. XU S. Numerical simulation of thermochemical non-balanced flow magnetohydrodynamic control[D]. Harbin: Harbin Institute of Technology, 2021.
[12] 欧吉辉, 赵磊, 陈杰. 有局部稀薄气体效应的高超声速流动数值模拟[J]. 空气动力学学报, 2019, 37(2): 193−200. doi: 10.7638/kqdlxxb-2018.0179 OU Jihui, ZHAO Lei, CHEN Jie. Numerical simulation of hypersonic flows with local rarefaction effect[J]. ACTA AERODYNAMICA SINICA, 2019, 37(2): 193−200. (in Chinese). doi: 10.7638/kqdlxxb-2018.0179
[13] 肖洪, 商雨禾, 吴迪, 等. 稀薄气体动力学的非线性耦合本构方程理论及验证[J]. 航空学报, 2015, 36(7): 2091−2104. XIAO H, SHANG Y H, WU D, et al. Nonlinear coupled constitutive relations and its validation for rarefied gas flows[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(7): 2091−2104. (in Chinese)
[14] 黄依峰, 曾舒华, 江中正, 等. 非线性耦合本构在高空侧向喷流中的数值研究[J]. 航空学报, 2022, 43(S2): 11−25. doi: 10.7527/S1000-6893.2022.27700 HUANG Y F, ZENG S H, JIANG Z Z, et al. Numerical study on high-altitude lateral jet based on nonlinear coupled constitutive relation[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(S2): 8−22 (in Chinese). doi: 10.7527/S1000-6893.2022.27700
[15] 曹竣哲, 刘沙, 钟诚文, 等. 基于非线性耦合本构关系模型对临近空间非平衡流动的模拟[C]//中国力学学会流体力学专业委员会. 第十二届全国流体力学学术会议摘要集, 2022. doi: 10.26914/c.cnkihy.2022.068769 [16] EU B C. Kinetic theory and irreversible thermodynamics[J]. NASA STI/Recon Technical Report A, 1992, 93: 24498.
[17] AHN J W, KIM C. An axisymmetric computational model of generalized hydrodynamic theory for rarefied multi-species gas flows[J]. Journal of Computational Physics, 2009, 228(11): 4088−4117. doi: 10.1016/j.jcp.2009.02.026
[18] 肖洪, 师羊羊, 商雨禾, 等. NCCR方程在近平衡气体流动区域的验证[J]. 载人航天, 2015, 21(3): 303−308,314. doi: 10.3969/j.issn.1674-5825.2015.03.015 XIAO H, SHI Y Y, SHANG Y H, et al. Validation of nonlinear coupled constitutive relations in near-equilibrium gas flows[J]. Manned Spaceflight, 2015, 21(3): 303−308,314. (in Chinese) doi: 10.3969/j.issn.1674-5825.2015.03.015
[19] MYONG R S. A generalized hydrodynamic computational model for rarefied and microscale diatomic gas flows[J]. Journal of Computational Physics, 2004, 195(2): 655−676. doi: 10.1016/j.jcp.2003.10.015
[20] 白贺之, 陈兵, 徐旭. 基于PNS方程的高超声速热化学非平衡喷管流动数值模拟[J]. 战术导弹技术, 2018(4): 25−31. BAI H Z, CHEN B, XU X. Numerical simulation of hypersonic nozzle flow in thermochemical nonequilibrium based on parabolized navier-stokes equation[J]. Tactical Missile Technology, 2018(4): 25−31. (in Chinese)
[21] 杨建龙, 刘猛. 电离对高超声速热化学非平衡气动热环境的影响[J]. 北京航空航天大学学报, 2018, 44(11): 2364−2372. YANG J L, LIU M. Influence of ionization on hypersonic thermo-chemical non-equilibrium aerodynamic thermal environments[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(11): 2364−2372. (in Chinese)
[22] 滕子昂, 周志峰, 张智超, 等. 高超声速磁流体流动控制数值模拟研究[J]. 气动研究与试验, 2024(1): 86−99. TENG Z A, ZHOU Z F, ZHANG Z C, et al. Numerical investigation of magnetohydrodynamics flow control[J]. Aerodynamic Research & Experiment, 2024(1): 86−99. (in Chinese)
下载:
计量
- 文章访问数: 2
- HTML全文浏览量: 0
- PDF下载量: 2
