Intelligent Prediction Method for Flow Field and Static Force Coefficients of Two-Dimensional Blunt Body Combined Sections under Steady Wind
-
摘要:
在结构断面设计与优化中，高效精准地获取气动性能具有重要意义。传统的气动选型方法，如风洞试验和计算流体动力学数值模拟，存在耗时且成本高昂的问题，特别是在处理结构断面设计参数多样性和优化方向不确定性的迭代计算任务时，其效率低下的问题尤为突出。本研究提出了一种基于深度学习代理模型的智能预测方法，专注于定常风下钝体二维组合断面的绕流流场及三分力系数的快速精准预测。具体而言，该方法采用类似图片的一致化形状表达来描述钝体组合断面的气动外形，具有不受断面形式限制的通用性；通过融合卷积注意力机制模块与残差模块构建神经网络架构，并利用均方误差来捕捉神经网络预测误差，实现了从气动外形到绕流流场及三分力系数的强非线性映射。研究结果表明，该方法在定常风条件下，对钝体二维组合断面的时均绕流流场、表面压力分布以及三分力系数的预测误差分别控制在3.7%、0.35%和6.25%以内，满足精度要求，且计算效率提升了4个数量级。该方法为定常风下钝体断面气动性能的快速预测提供了一种高效、实用的技术手段。
Abstract:In the design and optimization of structural cross-sections, the efficient and accurate evaluation of aerodynamic performance is of significant importance. Traditional aerodynamic evaluation methods, such as wind tunnel tests and computational fluid dynamics numerical simulations, are time-consuming and costly. This is particularly evident when dealing with iterative computational tasks involving numerous design parameters and uncertain optimization trajectories for structural cross-sections, as the inefficiency of traditional methods becomes more pronounced. To address these challenges, this study proposes an intelligent prediction method based on a deep learning surrogate model, focusing on the rapid and accurate prediction of flow fields around two-dimensional combined bluff body cross-sections and static force coefficients under steady wind conditions. Specifically, this method employs a unified image-like shape representation to characterize the aerodynamic shapes of bluff body combined cross-sections, ensuring broad applicability without being limited by specific cross-section configurations. By integrating convolutional attention mechanisms and residual modules to construct the neural network architecture and using mean squared error to capture prediction errors, the method achieves a highly nonlinear mapping from aerodynamic shapes to flow characteristics and static force coefficients. The results demonstrate that, under steady wind, the prediction errors for the time-averaged flow fields, surface pressure distributions, and static force coefficients of two-dimensional combined bluff body cross-sections are all within 3.7%, 0.35%, and 6.25%, respectively, thereby satisfying the accuracy requirements. Additionally, the computational efficiency is improved by four orders of magnitude compared to conventional methods. Consequently, this method provides an efficient and practical solution for the rapid prediction of aerodynamic performance for bluff body cross-sections under steady wind environments.
-
0. 引 言
结构断面设计是结构设计的关键环节[1-4]，断面形式直接影响结构的强度、承载力和整体稳定性。断面优化设计以优化气动力系数为目标，通过调整结构气动外形来改变气动力的分布与大小，从而有效改善结构的气动性能。然而，对于大型或复杂结构，其气动外形通常表现为非流线型的复杂钝体。相同的气动措施在不同基础外形结构上的减振效果可能不同，甚至截然相反。气动措施的多样性和优化方向的不确定性使得研究人员难以快速确定目标结构的有效气动外形调整方案。
目前，测定气动力系数常用的方法主要有风洞试验[5-6]和计算流体动力学（Computational Fluid Dynamics, CFD）数值模拟[7-9]。风洞试验虽然结果可靠，但存在试验周期长、成本高以及难以与优化算法实现实时交互等局限，制约了其在工程设计中的应用。相比之下，CFD数值模拟方法具有周期短、灵活性高的优势，已成为钝体气动选型的主要技术手段。从工程应用的角度出发，重点关注的是钝体绕流引发的平均流场变化及其整体作用效果。雷诺时均数值模拟（Reynolds-averaged Navier-Stokes, RANS）由于其鲁棒性和低计算成本，被广泛应用于相关研究中。然而，RANS方法采用了严格的时均化处理，这一过程会完全消除瞬态流动特征[10-11]。为解决这一问题，非定常雷诺时均数值模拟（unsteady Reynolds-averaged Navier-Stokes, URANS）在 RANS 的基础上，进一步考虑了流场中的时间变量，能够有效捕捉钝体绕流中典型的大尺度瞬态流动特征和气动力的周期性变化，为研究钝体绕流问题提供了更为有效的手段。
随着人工智能技术的快速发展和计算机硬件性能的不断提升，国内外学者开始将数据驱动方法应用于二维翼型、导弹、飞机等结构的气动力预测。早期研究主要集中在气动力的快速预测和参数化建模上。例如，陈海等[12]利用深度学习技术进行建模，将翼型几何图片作为卷积神经网络输入、气动系数作为输出，有效提高了翼型气动系数预测精度及模拟效率；Miyanawala等[13]基于欧拉距离场定义了气动外形的一致表达形式，实现了椭圆类气动外形的气动力预测；Guo等[14]以符号距离函数（signed distance function, SDF）为输入，利用深度学习神经网络的卷积编码与解码部分实现二维气动流场快速预测，为实时、交互式的气动外形设计优化开拓了空间。随着研究的深入，重点逐渐从简单的参数识别与分析，转向更为综合的风工程问题解决。Abbas等[15]使用人工神经网络来预测桥梁的气动弹性响应，结合数值分析和预测模型，为复杂的空气动力学现象提供了稳健高效的预测策略；李珂等[16]将钝体断面气动外形转化为图像数据，构建钝体断面气动外形到阻力系数的深度学习代理模型，有效提升了气动性能智能预测效率；Ribeiro等[17]进一步提出DeepCFD模型，以SDF和多类流区域信息为输入，为钝体断面的非均匀稳态层流的速度和压力场提供了更加高效的近似解。
尽管数值模拟在气动力研究中仍发挥着重要作用，但其精度的实现依赖于大规模网格及大量流场数据的划分，以及高性能计算集群的支持，这导致模拟计算时间较长，难以满足断面设计优化中对快速评估的需求。深度学习技术为这一问题开辟了新途径，特别是在处理断面设计参数多样性和优化方向不确定性导致的反复迭代计算时，其展现出显著的计算效率优势[18]。针对上述问题，本研究提出了一种基于深度学习的钝体二维组合断面绕流特性智能预测方法，致力于突破时域解耦难题，显著提高气动预测效率[19- 20]，为工程领域的快速气动选型提供技术支撑。
1. 气动预测模型数据集设计
深度学习代理模型并非“开箱即用”，其输入设计变量决定了模型能够“看到”和学习到的结构特征信息，输出响应值的准确性直接决定了模型学习的目标和方向。因此，需要设计可准确表达结构断面的气动外形信息的特征表达、可明确且有针对性地反映钝体结构的绕流特性的输出表达、匹配输入输出映射关系的神经网络架构。在实现输入、输出表达的同时，提高信息传递效率。
1.1 气动外形的一致化输入表达
采用结构断面的角点坐标作为结构几何特征表达是最直接的方式，但这种方法存在一定的局限性：基于原始角点坐标训练的神经网络无法处理未知的结构组合断面形状，难以满足形状选择多样性和频繁调整的需求。为了解决数据异构问题，本研究在Chen等[21]提出的0-1距离场基础上，借鉴Miyanawala等[13]提出的形状表达方法，提出了一种适用范围更广的“一致化形状表达”方法。
李珂等[16]同样关注到传统输入方式的局限，提出通过距离场强化输入信息与边界层的联系，以顺风向坐标场和横风向坐标场弥补距离场信息的不足，以图像形式描述钝体断面气动外形特征。这种图像形式的距离场、顺风向坐标场和横风向坐标场的思想与本研究提出的“一致化形状表达”思路相符。然而，李珂等的输入设计仅针对单个钝体断面（如正六边形、圆形、矩形和正菱形），在面对复杂的结构组合断面时，其方法可能难以准确捕捉组合断面的气动外形特征。
为了有效反映钝体组合断面的气动外形，本研究进一步拓展和优化了输入设计。具体实现时，本研究充分考虑了结构边界层的影响以及流场的流动特征，并采用距离场、顺风向坐标场和横风向坐标场来描述断面气动外形，将其作为神经网络的输入参数，最终定义了一系列“一致化表达”函数，如公式（1～3）所示：
“一致化形状表达”距离场定义为：
Ddist,j=(min (1) “一致化形状表达”顺风向坐标场定义为：
D_{x, j} = \frac{\beta}{1+\mathrm{e}^{-x_j / B}} (2) “一致化形状表达”横风向坐标场定义为：
D_{y, j} = \frac{\beta}{\mathrm{e}^{-\left|y_j\right| / B}} (3) 式中： {D}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t},j} 为结构断面距离场函数； {D}_{x,j} 为结构断面顺风向坐标场函数； {D}_{y,j} 为结构断面横风向坐标场函数； \mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t} (·)为计算两点坐标之间的欧氏距离函数； {r}_{j} 代表结构断面周围空间各点的坐标； j 为区域空间各点的索引； {r}_{i,\Gamma } 代表结构组合断面第 i 个形状边界各点的坐标； \beta 为结构断面权重参数，采样点在边界上或者边界内时 \beta 为0，反之为1； B 为结构断面特征长度； {x}_{j} 和 {y}_{j} 分别代表断面周围空间 j 点的 x 坐标和 y 坐标。
1.2 绕流特性的时均输出表达
为平衡计算精度与效率的需求，近年来基于数据驱动的代理模型方法受到了广泛关注。这类方法通过建立几何参数与气动力系数的直接映射关系，绕过N-S方程主导的压力场演化过程，来探究气动外形对绕流特性的影响机制。然而，现有的气动力系数代理模型大多采用“端到端”的建模策略，即直接从几何参数预测积分得到的气动力系数。这种建模方式虽然计算高效，但其直接跳过了压力场局部采样、表面压力积分等多个关键的数据处理环节，导致模型输入与输出之间的物理联系被弱化，无法有效感知流动分离、涡脱落等微观流动现象的影响。
从流体力学的控制方程出发，气动力系数本质上是表面压力分布的积分结果，即：
C_L = \dfrac{1}{\dfrac{1}{2} \rho U_{\infty}{ }^2 A} \oint_S\left(p-p_{\infty}\right) \mathbf{n} \cdot \mathbf{e}_1 \mathrm{d} S (4) C_D = \dfrac{1}{\dfrac{1}{2} \rho U_{\infty}{ }^2 A} \oint_S\left(p-p_{\infty}\right) \mathbf{n} \cdot \mathbf{e}_{\mathrm{d}} \mathrm{d} S (5) C_m = \dfrac{1}{\dfrac{1}{2} \rho U_{\infty}{ }^2 A B} \oint_S\left(p-p_{\infty}\right)(\boldsymbol{r} \times \mathbf{n}) \cdot \mathbf{e}_{\mathrm{m}} \mathrm{d} S (6) 式中： {C}_{L} 为升力系数， {C}_{D} 为阻力系数， {C}_{m} 为升力矩系数， \rho 为流体密度， {U}_{\infty } 为来流速度， A 为特征面积， B 为特征长度， p 为表面压力， {p}_{\infty } 为来流静压， \mathbf{n} 为表面单位法向量， \mathit{r} 为表面微元到参考点的位置矢量， {\mathbf{e}}_{\mathrm{l}} 为升力方向单位向量, {\mathbf{e}}_{\mathrm{d}} 为阻力方向单位向量， {\mathbf{e}}_{\mathrm{m}} 为力矩轴方向单位向量， \mathrm{d}S 为结构表面微分面积。
针对上述问题，本研究提出了一种绕流流场的时均结果描述方法，把进一步的数据处理环节独立于模型预测，增强模型输入与输出的逻辑关系。该方法通过CFD数值模拟计算，运用URANS模拟手段，对周期性流场进行相位平均处理，进而得到包含丰富流场结构物理特征的稳定时均场，并将其作为结构气动性能的输出。
1.3 模型架构设计
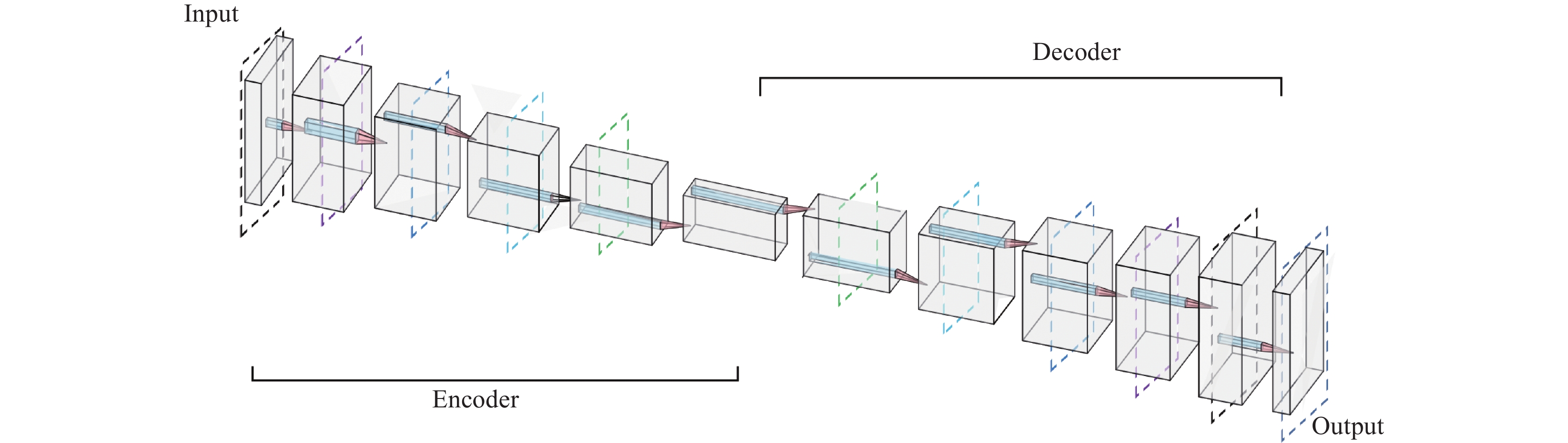
本研究提出了一种基于深度学习的编码器-解码器（decoder-encoder）架构，如图1所示。该架构采用层次化特征提取与重构的设计理念，通过融合残差模块和注意力机制，在保持网络深度的同时确保特征传递的有效性。
1.3.1 编码器
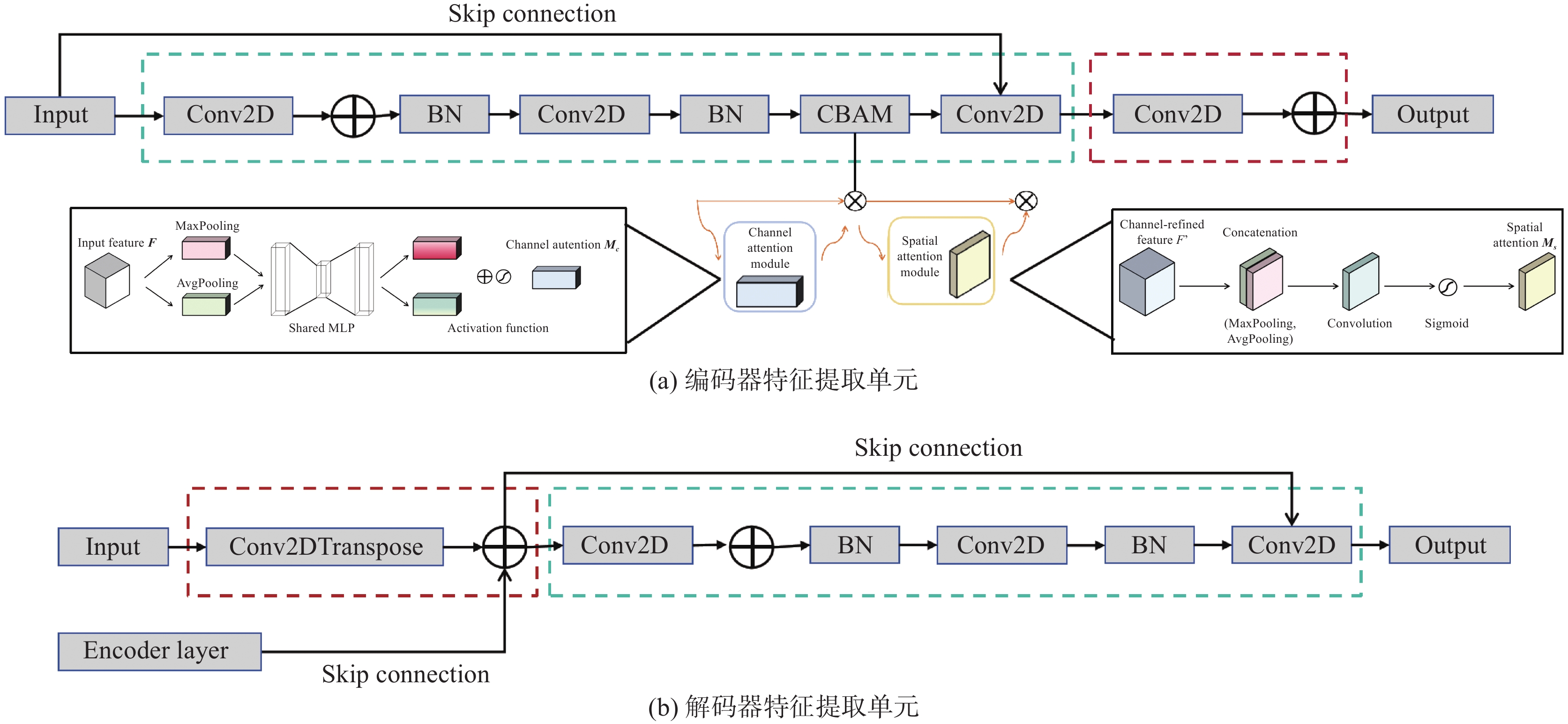
编码器部分采用多级特征提取策略，通过层次化卷积运算逐步构建气动外形的深层特征表示。输入数据经过逐步被压缩图像的空间信息，并通过特征图的学习捕捉更加全面的气动外形特征，这一过程通过下采样（downsampling）的编码器特征提取单元实现。如图5（a）所示，编码器特征提取单元主要包含基础特征提取（红色框内）和特征增强（绿色框内）两个关键环节。
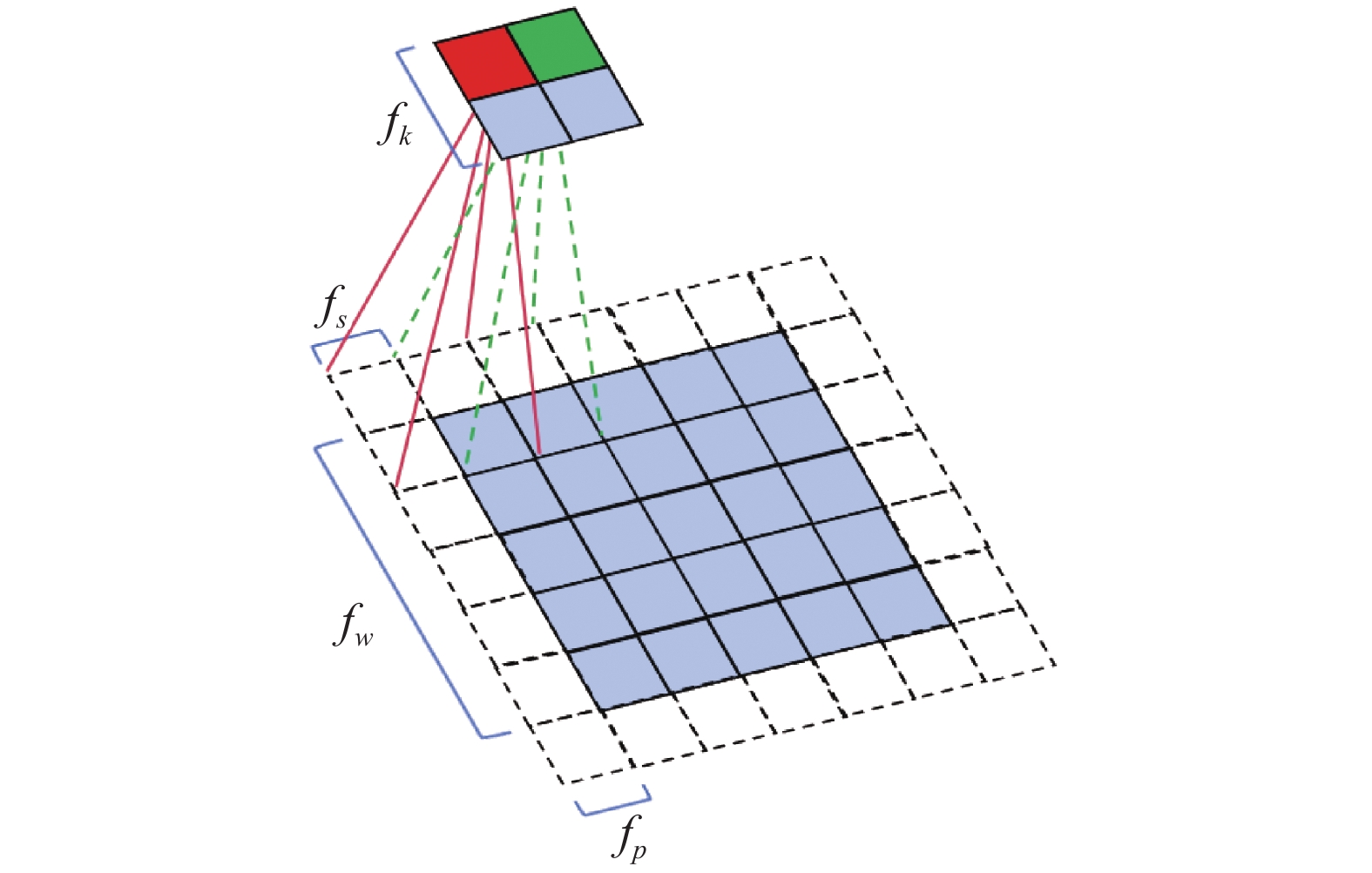
基础特征提取环节通过卷积运算配合非线性激活函数进行特征变换。采用渐进式下采样策略，在保持特征图结构的同时逐步扩大感受野，实现从局部到全局的特征提取。每级基础特征提取单元包含一个基础卷积单元，如图2所示。采用卷积过程实现下采样，通过在输入数据上滑动卷积核，对局部区域进行加权求和，从而提取出数据中的局部特征。其数学计算过程可分解为：
f_w^{\prime} = \frac{\left(f_w+2 f_p-f_k\right)}{f_s}+1 (7) 式中： {f'_w} 代表卷积后产生的特征图大小， {f}_{w} 代表原始输入矩阵大小， {f}_{p} 代表填充补零层数， {f}_{k} 代表卷积核大小， {f}_{s} 代表步幅。
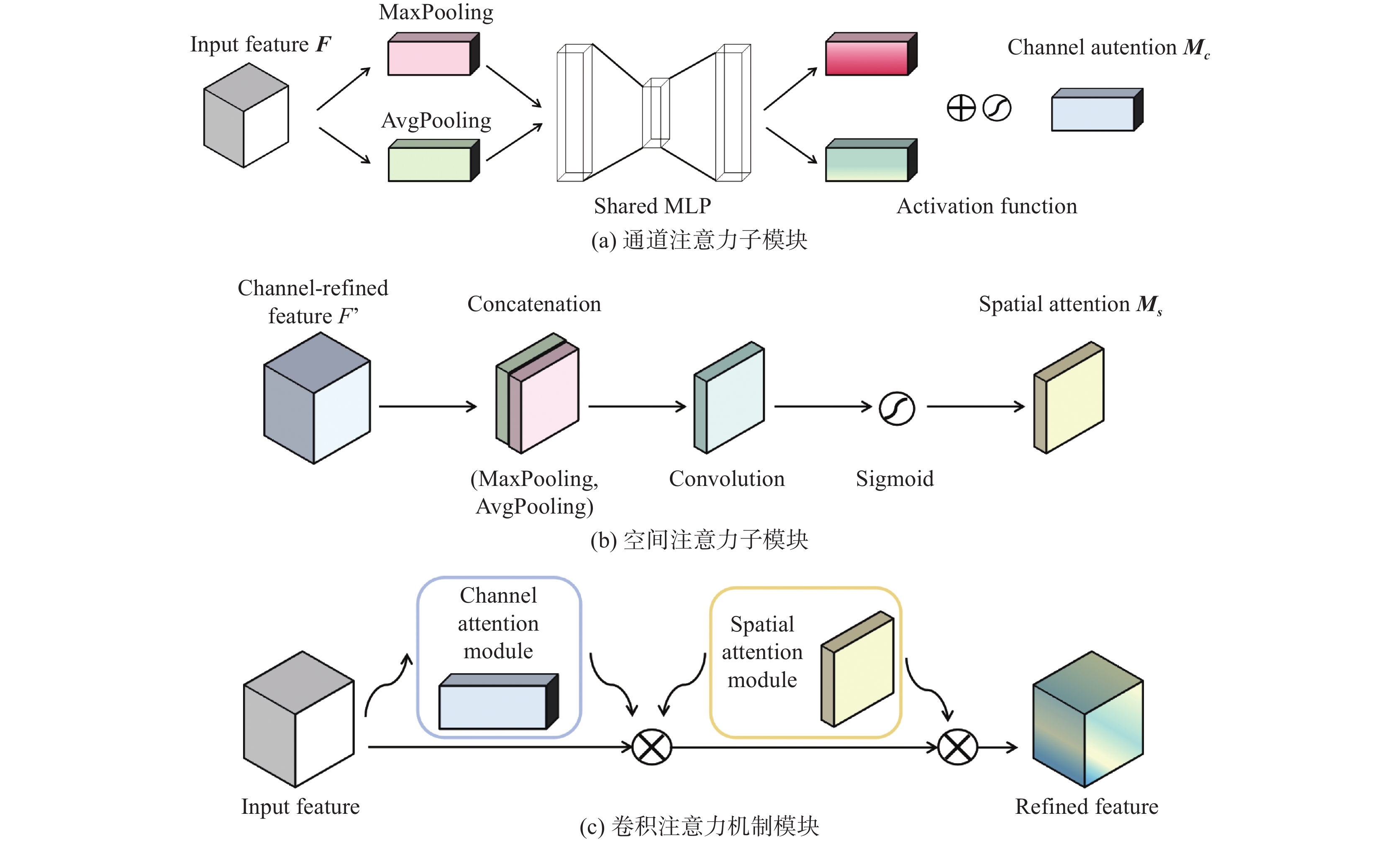
特征增强环节主要采用引入残差学习模块和卷积注意力增强机制[22]。首先引入如图3（c）所示的卷积注意力机制（convolutional block attention module, CBAM），构建了通道-空间协同特征重校准机制。该机制利用图3（a）的通道注意力（channel attention）子模块，通过全局池化与多层感知机（multilayer perceptron, MLP）生成通道权重；利用图3（b）的空间注意力（spatial attention）子模块，通过卷积操作生成空间权重，动态加权关键特征通道，聚焦复杂区域流场，对气动外形输入特征进行逐步增强，使得网络能够自适应地调整对输入特征的关注程度。其数学计算过程分解为：
M_C = \sigma\left(\operatorname{MLP}\left(F_{\text {maxpooling }}+F_{\text {avgpooling }}\right)\right. (8) M_S = \sigma\left(\operatorname{Conv}\left(F'_{ {\mathrm{maxpooling}} },\; F'_{\text{avgpooling }}\right]\right) (9) \left.F_1 = M_S(M c(F) \otimes F) \otimes\left(M c\left(F^{\prime}\right) \otimes F^{\prime}\right)\right) (10) 式中： {M}_{C} 代表通道权重矩阵； {M}_{S} 代表空间权重矩阵； {F}_{1} 代表经卷积注意力机制加权的特征图； \sigma 代表非线性激活函数； \mathrm{M}\mathrm{L}\mathrm{P} 代表共享多层感知机，即多层神经网络堆叠而成的架构； \mathrm{C}\mathrm{o}\mathrm{n}\mathrm{v} 代表卷积运算； F 代表初始特征图； \mathrm{m}\mathrm{a}\mathrm{x}\mathrm{p}\mathrm{o}\mathrm{o}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{g} 代表全局最大池化； \mathrm{a}\mathrm{v}\mathrm{g}\mathrm{p}\mathrm{o}\mathrm{o}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{g} 代表全局平均池化; {F}' 代表经过通道加权的特征图； \otimes 代表逐元素乘法。
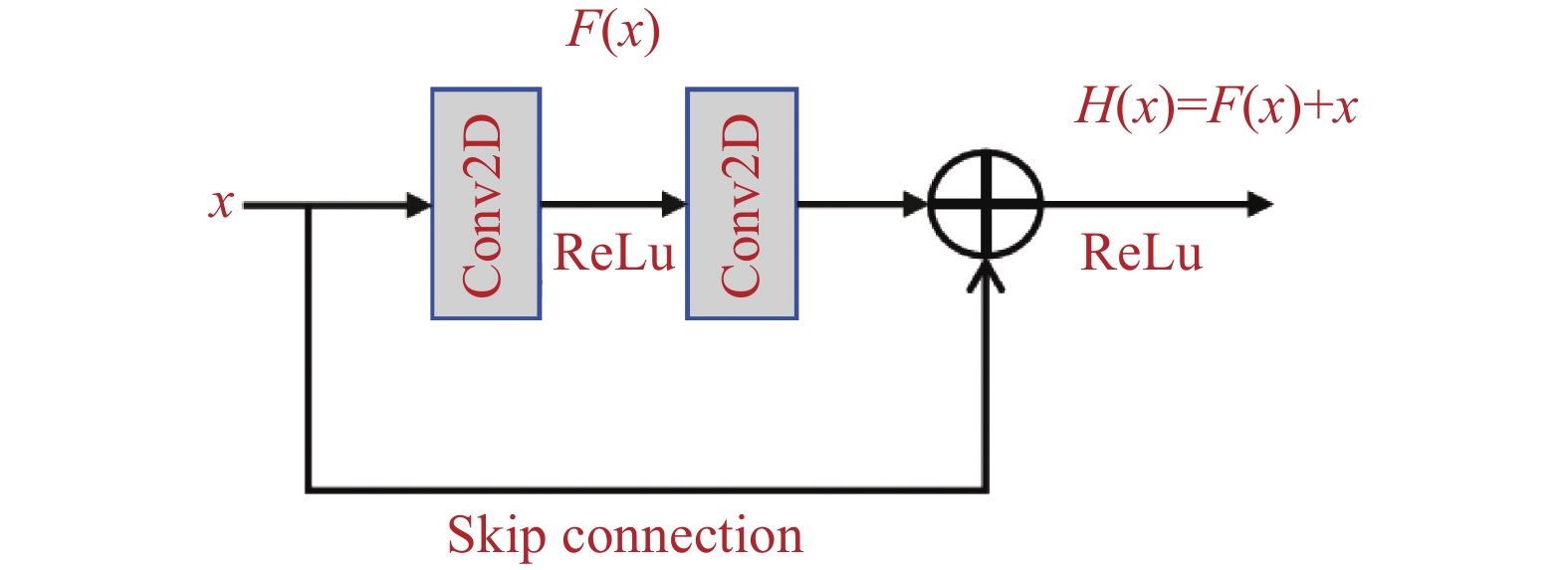
其次，引入残差模块（residual block, ResBlock），通过跨层连接保留原始特征信息，缓解深度网络训练过程中出现的梯度消失问题，确保训练稳定性。如图4所示，每个ResBlock包含两个卷积层和批标准化层（batch normalization, BN），并通过特征叠加将输入直接与输出相加，从而保留原始输入的信息。其数学计算过程分解为：
H\left(x\right) = F\left(x\right)+x (11) 式中： H\left(x\right) 代表经过残差模块处理后的输出特征图； F\left(x\right) 代表残差模块中由两个卷积层和批标准化层对输入特征图进行一系列非线性变换后得到的残差特征图，即需要网络学习的输入与目标输出之间的差异部分； x 代表输入到残差模块的原始特征图。
残差连接本质上构建了CFD数值模拟中微分方程数值解中的欧拉离散格式，其迭代过程可建模为：
x_{t+\Delta t} = x_t+F\left(x_t, \theta_t\right) (12) 式中： x_{t+\Delta t}代表 {t+\Delta t} 时刻物理量； {x}_{t} 代表 t 时刻物理量； F({x}_{t},{\theta }_{t}) 代表在t时刻，由当前物理量 {x}_{t} 以及对应时刻模型参数 {\theta }_{t} 所决定的变化量函数。
本研究进一步建立残差注意力模块，通过嵌入通道-空间注意力机制的残差模块实现物理敏感区域的动态特征增强，一方面确保残差连接跨层信息的完整性，另一方面避免信息的过度压缩或失真。
1.3.2 解码器
解码器采用与编码器对称式结构，采取多层次特征融合与渐进式上采样策略，通过转置卷积（Conv2DTranspose）逐步恢复空间分辨率，并利用跳跃连接将编码器中的高层特征与解码器的低层特征结合，从而实现对流场输出的精确预测，这一过程通过上采样（upsampling）操作的解码器特征提取单元实现。如图5（b）所示，解码器特征提取单元包含基础特征提取（红色框内）和特征增强（绿色框内）两个关键环节。
基础特征提取环节使用Conv2DTranspose学习将低分辨率的特征图恢复至高分辨率图像，逐步恢复图像的空间分辨率，类似于传统的上采样操作。每级上采样模块包含基础特征变换单元，通过批归一化和非线性激活处理确保特征分布的稳定性。该过程可表示为：
f_w^{\prime} = \left(f_w-1\right) f_s+f_k-2 f_p (14) 特征增强环节融合了注意力机制和跨层连接技术。通过嵌入改进的注意力模块，解码器能够动态调整对关键流场特征的关注程度，采用密集的跳跃连接架构将编码器各层特征与解码器对应层特征深度融合，既保留了高级特征的语义信息，又补充了低级特征的空间细节。
2. 数据集获取
本研究基于Python语言开发了一套自动化数据处理程序，实现了结构组合断面气动外形和气动性能信息的自动化处理与高效获取。
2.1 算例设置
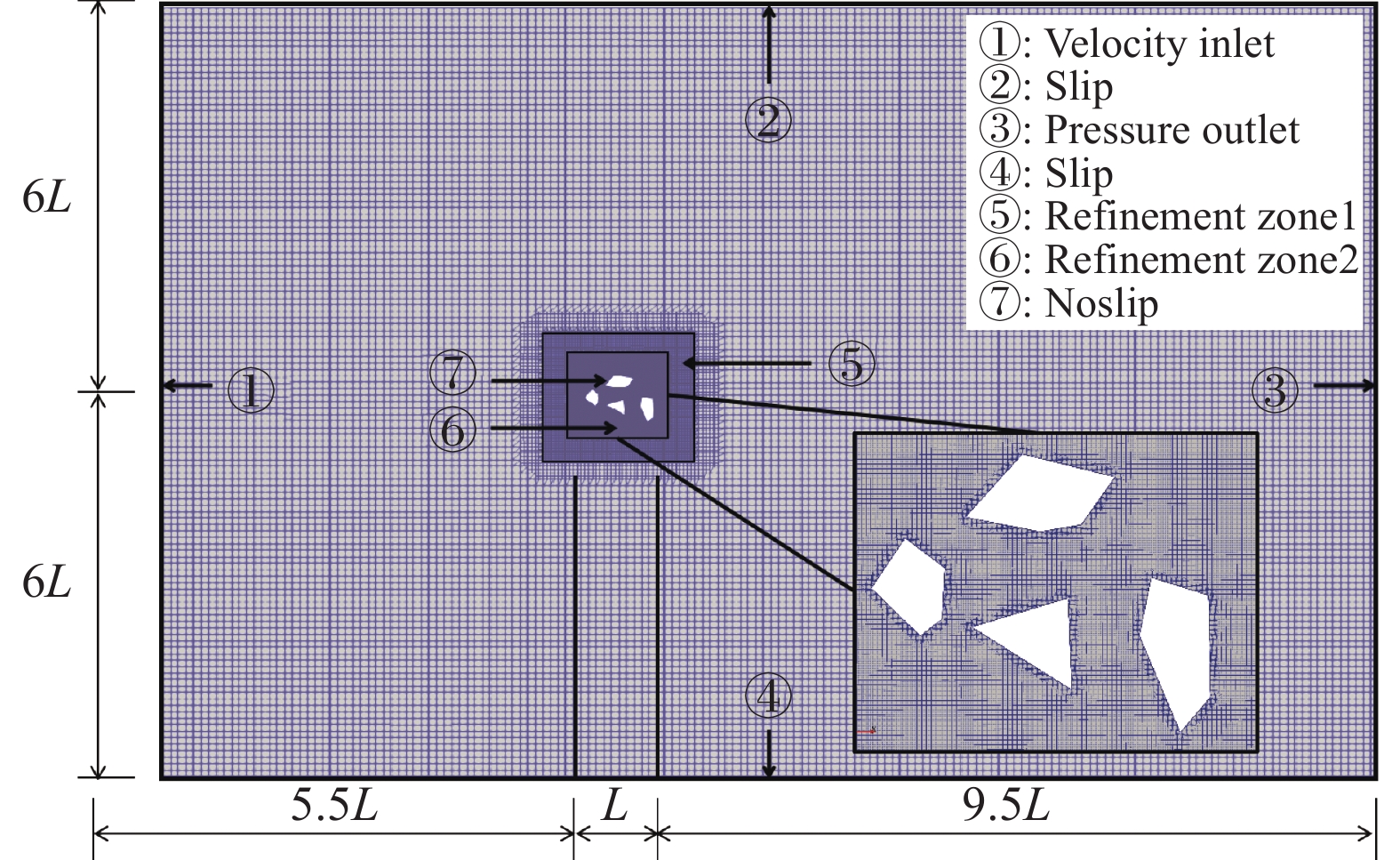
为获取结构断面的气动性能数据，本研究基于开源平台OpenFOAM开展CFD数值模拟，如图6所示，具体设置如下：
1） 控制方程与计算域设置：采用二维URANS方法对结构断面样本进行不可压缩流场分析。计算域为矩形，长度设定为15L，宽度设定为12L，其中L为区域流场总宽度。
2） 湍流模型与边界条件：湍流模型采用k-ω SST剪切应力输运模型；边界条件中，入口处速度场Uinlet、湍流比耗散ω和湍流动能k采用狄利克雷条件，出口压力poutlet及压力场采用狄利克雷条件，出口边界的速度、比耗散率和湍动能采用诺依曼条件，上、下边界采用滑移边界条件，壁面采用无滑移边界条件。
3） 网格生成与质量验证：利用snappyHexMesh生成非结构化网格，网格总数约为77.8万。边界层网格的y+值始终小于1，第一层相对厚度为
0.1167 ，边界层相对厚度为0.5。4） 求解器与时均处理：采用pimpleFoam求解器进行流场求解，该求解器具有良好的稳定性和准确性，适用于复杂流动问题的求解。待结构断面升力和力矩稳定后，对稳定流场周期内的流场进行时均处理，得到时均输出流场，
2.2 网格无关性验证
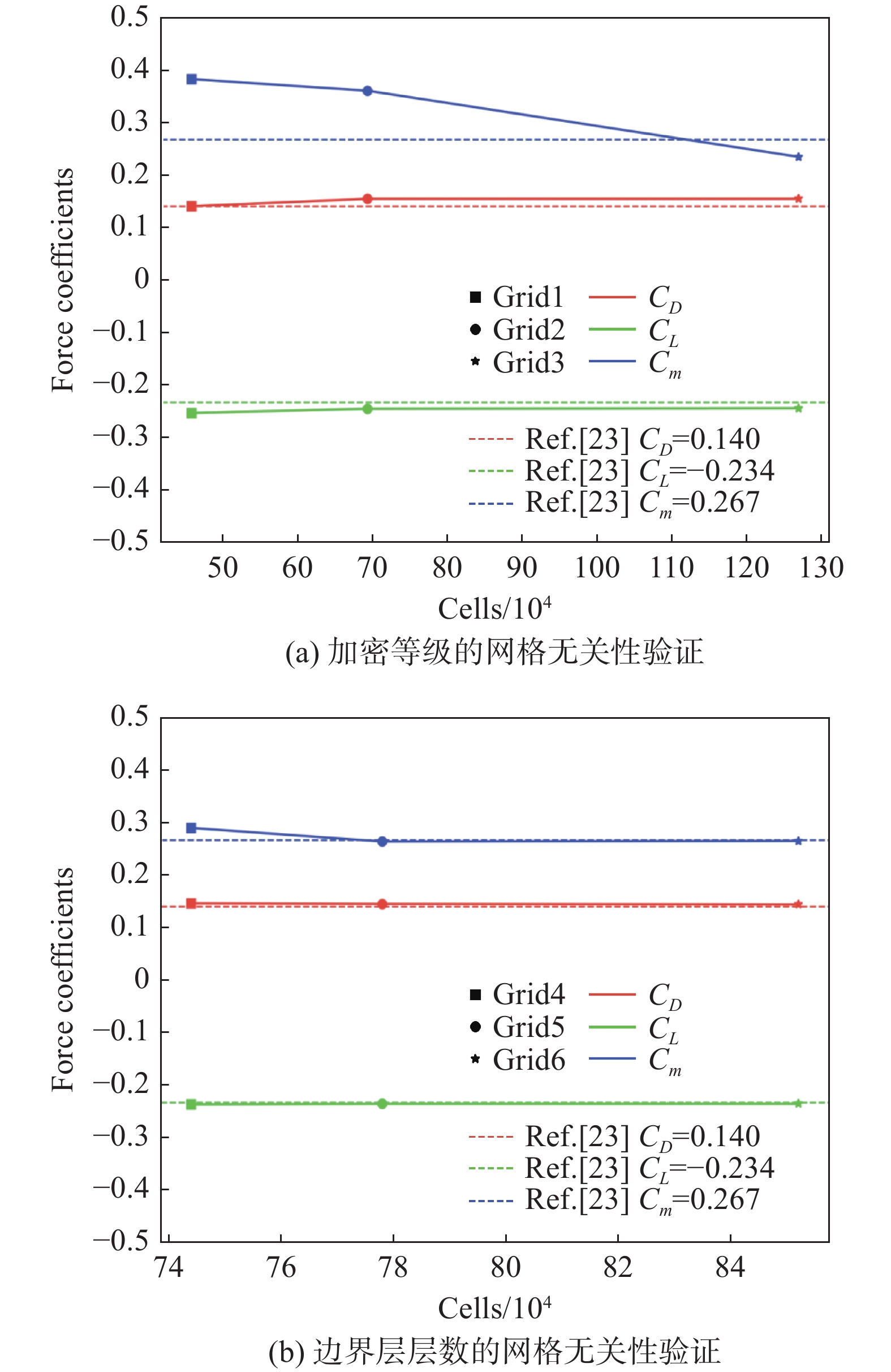
本研究针对二维双箱梁桥，选取 6组不同网格结构研究网格密度对数值模拟结果的影响，网格的差异主要在于加密区的设置区域、加密等级和边界层厚度等，边界层保持相同的离散化。计算结果与Álvarez等[23]的开槽双箱梁数值模拟数据进行对比验证，所有模拟均在Re = 6.61×104、来流风速1 m/s、风攻角0°条件下进行，具体如表1所示。
表 1 网格无关性验证Table 1. Grid independence studyCells/104 Refinement level Boundary layer/layers C_D C_L C_m {\mathrm{error}}_{CD}/% {\mathrm{error}}_{CL} /% {\mathrm{error}}_{Cm} /% Álvarez A J[23] — — — 0.140 –0.234 0.267 — — — Grid 1 45.8 4 0 0.140 –0.254 0.382 0 8.55 43.07 Grid 2 69.3 5 0 0.154 –0.246 0.360 10.00 5.13 34.83 Grid 3 126.9 6 0 0.154 –0.245 0.234 10.00 4.70 12.36 Grid 4 74.8 5 2 0.146 –0.237 0.290 4.29 1.28 8.61 Grid 5 77.8 5 3 0.145 –0.236 0.264 3.57 0.85 1.12 Grid 6 85.2 5 4 0.144 –0.236 0.265 2.86 0.85 0.75 首先分析表面加密等级对模拟结果的影响，对比Grid 1、Grid 2、Grid 3的计算结果（见表1和图7（a））可知，3种不同表面加密等级网格的计算结果非常相似，尤其是Grid 2和Grid 3，可见中等密度网格Grid 2（加密等级5，网格数77.8万）可以以较低的计算成本提供空间离散化的可靠结果，继续提升加密等级对结果改善有限。其次分析添加不同边界层层数对模拟结果的影响，对比Grid 4、Grid 5、Grid 6的计算结果（见表1和图7（b））可知，添加3层边界层为最佳选择，可以避免因层数冗余导致的计算误差扩大与资源浪费。从与Álvarez等[23]的数值模拟结果的一致性而言，当前网格方案下，所提出的二维URANS方法能够反映结构绕流的基本流动特征，Grid 5为最优网格设置。
2.3 批量化数值模拟
为实现CFD数值模拟流程的自动化与批量化操作，本研究致力于将上述CFD数值模拟流程集成到Shell中。通过Shell脚本与Python程序的深度协同，构建一一对应的钝体组合断面气动外形与绕流流场数据集。这一过程涉及多个步骤，下面将详细阐述。
首先，在坐标原点处设定一个单位长度的二维正方形空间区域，作为整个建模过程的基础区域。在此区域内，根据初始断面具体的参数设置（如表2所示），随机生成若干不重叠区域。在每个子区域内，按照初始断面参数设置生成相应的二维形状，例如三角形、矩形等。利用组合断面边界点及周围空间点坐标，依据1.1节和1.2节距离场、顺风向坐标场和横风向坐标场的定义，将断面几何特征转化为一致化形状表达。图8展示了形状个数为2、3、4时结构断面形状的顺风向坐标场、横风向坐标场和距离场。其中，距离场中颜色深浅表示空间区域各点与结构气动外形边界的距离远近，顺风向坐标场和横风向坐标场则分别反映了空间区域各点的流动路径和分布特征信息。
表 2 气动外形的主要参数特征Table 2. Main characteristic parameters of aerodynamic shapesparameter Shapes Size Vertices Pixels/px min 2 0.2 3 256 max 6 0.5 7 256 注：表中Shapes表示组合断面中形状的个数；Size表示限制单个断面最大尺寸，m；Vertices表示组合断面单个形状的边数；Pixels代表采样的分辨率，像素（px），每个像素点pij的坐标通过–0.5–1/256+1/256i和–0.5–1/256+1/256j获得，其中i、j的取值范围均为[0,256]。 其次，针对生成的大量钝体组合断面模型，Python自动化程序将其自动导入CFD 模拟环境，将钝体几何外形信息转换为obj建筑几何文件，存储至CFD数值模拟算例的constant/triSurface目录，并依据不同钝体组合断面的特征，更新system/blockMesh、system/snappyexMeshDict以及后处理函数等文件。
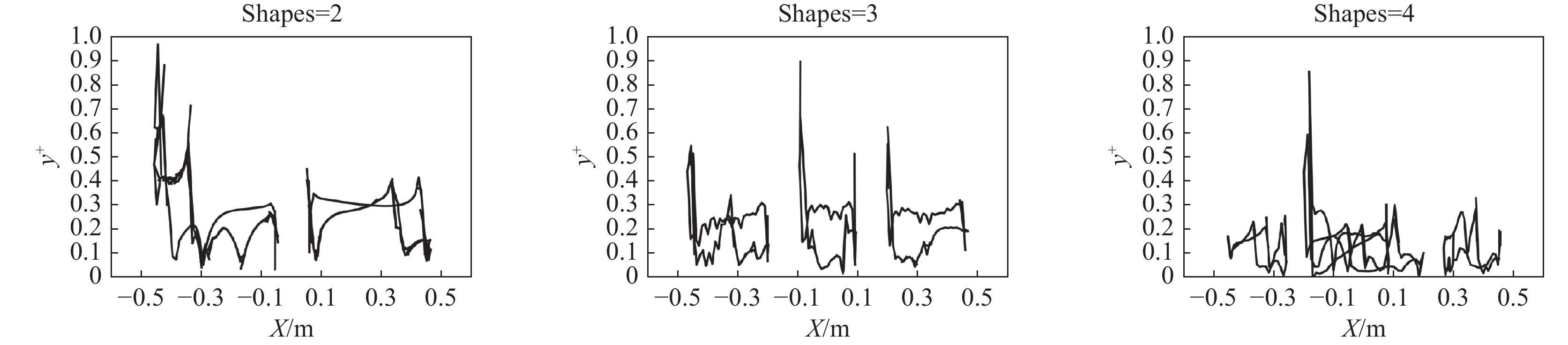
然后，程序指令调用blockMesh工具构建六面体背景网格，为非结构化网格生成搭建框架，再通过snappyHexMesh-overwrite命令，使用snappyHexMesh工具经细化网格、网格捕捉及添加边界层操作生成非结构化网格。依据meshQualityControls参数检查网格质量，若不达标，程序自动回溯调整参数并重新生成，直至满足CFD模拟要求。图9 显示初始组合断面个数为 2、3、4 时典型断面的y+值分布，所有工况下y+值均小于1，符合网格生成质量要求。
最后，流场计算阶段采用pimpleFoam求解器进行瞬态模拟，严格遵循controlDict文件设定的时间步长、计算时长和收敛准则等参数。计算中实时监测各物理量残差变化，残差未达收敛标准时，求解器自动调整迭代参数以保证计算稳定和结果可靠，同时程序定期输出计算状态信息。
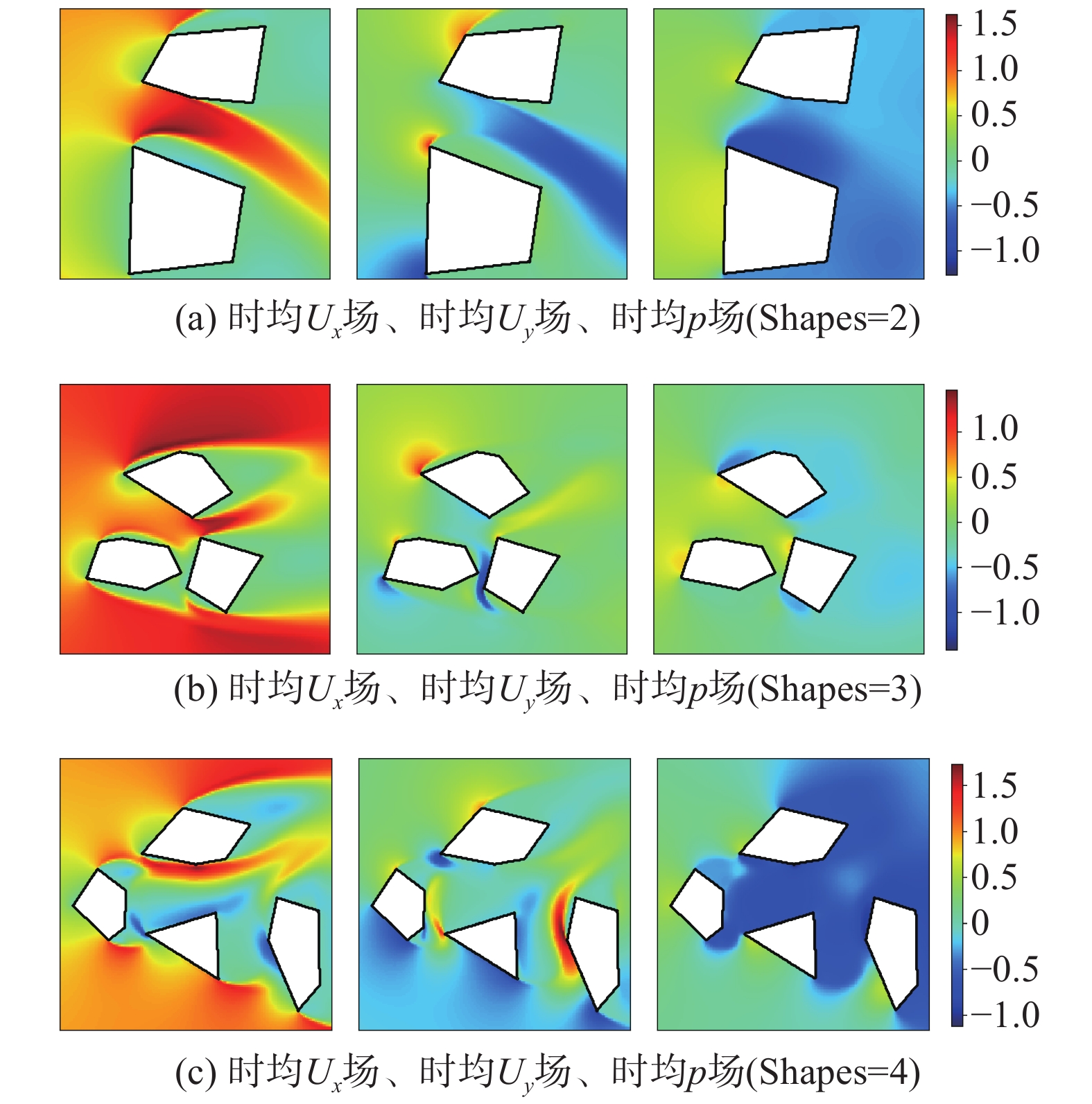
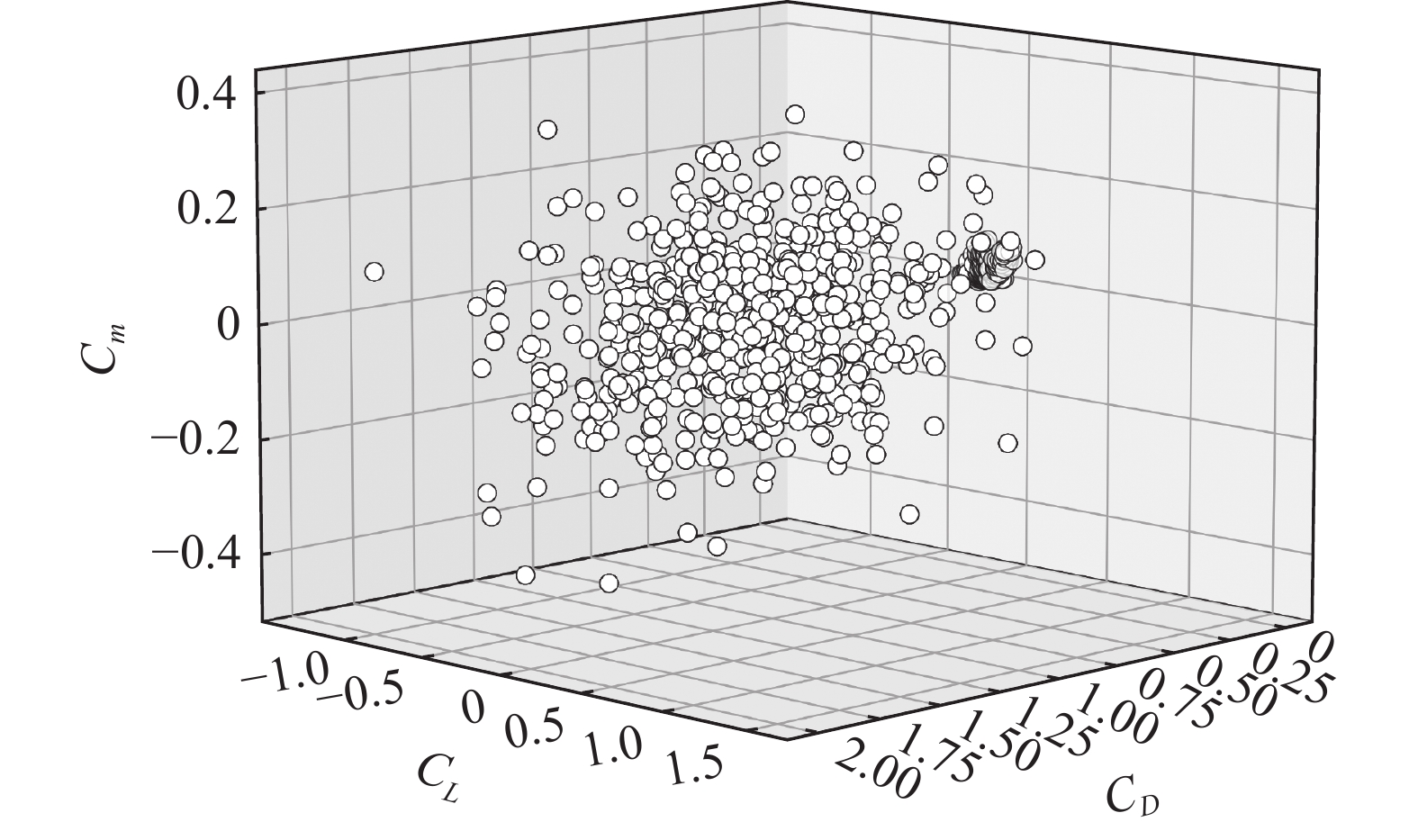
计算完成后，程序按预设规则存储流场数据。速度场、压力场以及力系数等关键物理量以OpenFOAM标准格式保存，所有输出数据采用规范命名以确保可追溯性。图10分别展示了初始组合断面个数为2、3、4时典型断面的时均流场，图11展示了批量数数值模拟的
1000 个算例的三分力系数分布。2.4 数据增强
基于上述批量化数值模拟程序，本研究得到了
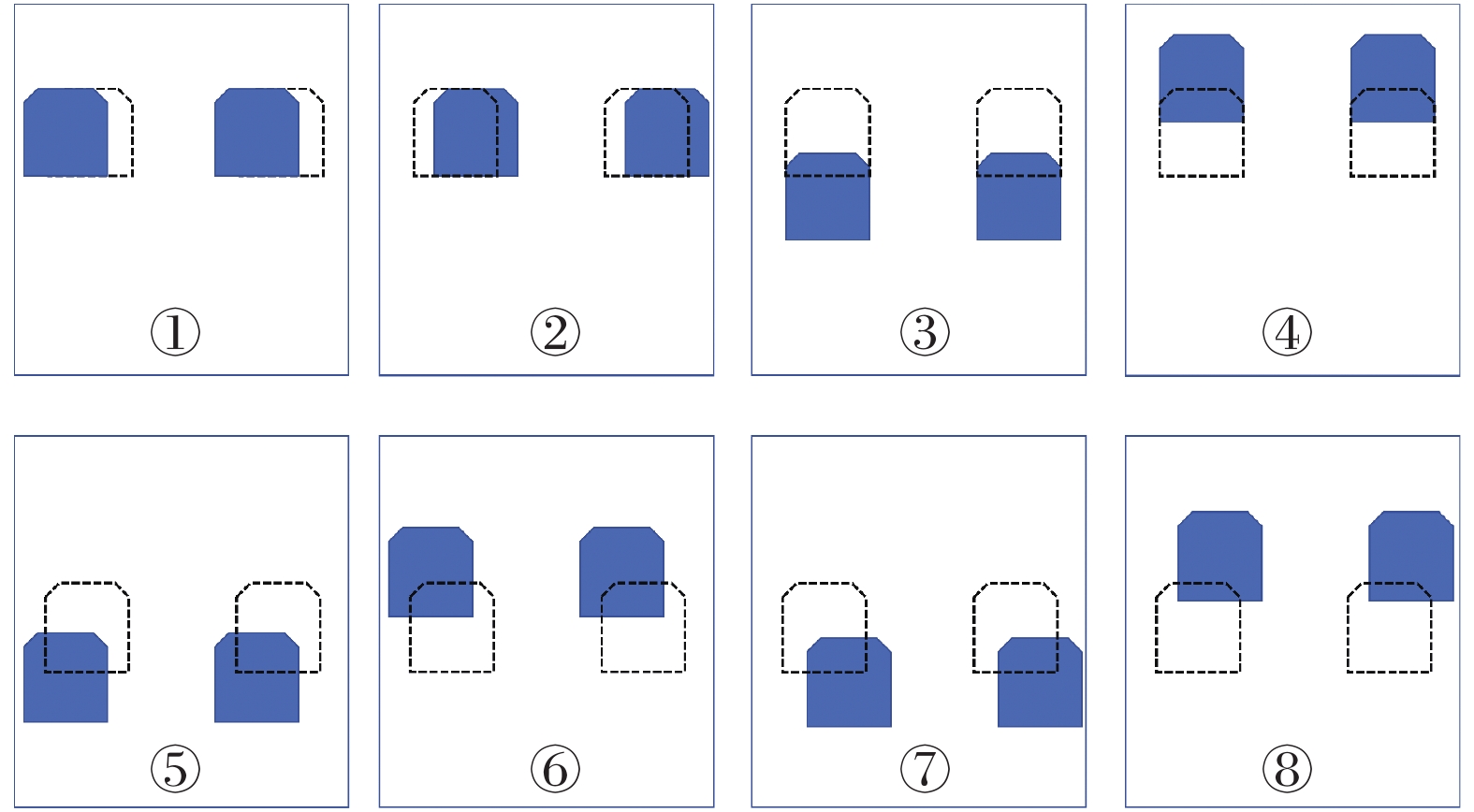
1000 组钝体组合断面的气动外形与绕流流场数据。鉴于该数据集源于CFD数值模拟计算域的局部区域采样的特殊性，本研究提出在维持组合断面几何特征不变的情况下，通过改变采样区域范围获取时均流场输出，并结合气动外形特征设计生成相应的距离场、顺风向坐标场和横风向坐标场的方法，快速扩展数据集规模，从而增强深度学习代理模型对复杂流场特征的提取能力。具体实现方式为：通过建立a、b、c、d四个移动距离公式（公式15～18）确定不同方向移动距离，数据经单方向和组合方向平移实现增强，前者生成左、右、上、下平移数据，后者实现组合平移数据增强。数据增强方法如图12所示，图中虚线框代表数据在增强前的原始状态，实线框代表经过平移变换的数据。
a = -(0.5-x \min ) / 2 (15) b = (0.5-x \max ) / 2 (16) c = -(0.5-y \min ) / 2 (17) d = (0.5-y \max ) / 2 (18) 式中： a 、b分别代表数据在水平方向上向左、向右的移动距离； c 、d代表数据在垂直方向上向上、向下的移动距离。
综上所述，构建的输入数据张量为(
9000 ，256，256，3)，输出数据张量为(9000 ，256，256，3)。其中，输入数据张量中，“9000 ”代表数据样本的数量，意味着有9000 个独立的数据单元用于模型训练或分析；“256，256”表示每个数据样本在空间维度上的尺寸为256×256，这通常可以理解为图像类数据的像素分辨率，即每个样本可看作是一张256×256像素的图像；最后的“3”则对应数据样本的通道数，代表1.1节的一致化形状表达距离场、横风向坐标场以及顺风向坐标场。同理，输出数据张量(9000 ，256，256，3)也遵循相同的解释逻辑，其结构与输入数据张量一致，意味着模型的输出同样为9000 个具有256×256像素分辨率且包含时均输出场三通道的图像数据。3. 模型训练
3.1 模型搭建
利用采样得到的钝体断面气动外形样本以及其对应的时均流场作为数据集搭建网络架构。具体地，编码器通过5级下采样逐步提取几何特征中的多尺度流场关联特征，每级包含带CBAM注意力机制的残差注意力模块，可自适应聚焦关键流动区域。本研究选定 256×256 像素作为输入分辨率，由于有3个不同的场作为输入，因此实际输入数据是一个 256×256×3 的三维矩阵。解码器通过对称的上采样结构重构流场细节，最终输出与输入同分辨率的时均流场预测结果（256×256×3）。
为了找到上述架构的理想设置，主要针对各层是否采取残差注意力模块、通道数以及各层卷积核数、学习率等超参数进行测试，如表3所示，每个架构可以假设24种设置。本研究在超参数搜索过程中进行了大量的评估，并确认各超参数设置如表3所示。
表 3 超参数优化区间Table 3. Hyperparameter optimization spaceParameters Range Setting Filter [8,16,32,64] 32 Kernel [3×3, 7×7] 7×7 Lr [1×10–2, 1×10–3, 5×10–3] 1×10–2 注：表中Filter表示首层隐藏层通道数量；Kernel表示卷积注意力模块的卷积核尺寸；Lr表示初始学习率。 通过以上结构，本研究构建了一个深度学习代理模型，该模型采用编码器-解码器结构，融合卷积注意力模块与残差模块以进行特征提取和流场重构。通过对比测试各层是否采用该模块，确定了模型具体架构和参数，如表4所示。
表 4 神经网络架构及参数Table 4. Neural network structure and parametersEncoder-Decoder Layer ResBlock CBAM Input Shape Output Shape Param downsampling Conv2D-1 True [1,256,256,3] [1,128,128,32] 896 downsampling Conv2D-2 True True [1,128,128,32] [1,64,64,64] 18496 downsampling Conv2D-3 True True [1,64,64,64] [1,32,32,128] 73856 downsampling Conv2D-4 True True [1,32,32,128] [1,16,16,256] 295168 downsampling Conv2D-5 True True [1,16,16,256] [1,8,8,512] 1179648 upsampling Conv2DTranspose-1 True [1,8,8,512] [1,16,16,256] 1179648 upsampling Conv2DTranspose-2 True [1,16,16,256] [1,32,32,128] 295168 upsampling Conv2DTranspose-3 True [1,32,32,128] [1,64,64,64] 73856 upsampling Conv2DTranspose-4 True [1,128,128,32] [1,128,128,32] 18496 upsampling Conv2DTranspose-5 [1,256,256,16] [1,256,256,16] 4624 Conv2D-6 [1,256,256,16] [1,256,256,3] 435 注：表中“Encoder-Decoder”代表编码器-解码器架构类别；“Layer”为网络层名称；“ResBlock”代表是否使用残差块（True为使用）；“CBAM”代表是否使用卷积块注意力模块（True为使用）；“Input Shape”为各层输入数据的形状，依次代表样本数量、高度维度、宽度维度和通道数；“Output Shape”为各层输出数据形状，依次代表样本数量、高度维度、宽度维度和通道数；“Param”为该层的参数量。 3.2 模型训练设置
本研究采用均方误差（mean squared error, MSE）作为损失函数，用于衡量预测结果与真实值之间的差异。其数学表达式为：
E = \frac{1}{n} \sum_{i = 1}^n\left(y_i-\hat{y}_i\right)^2 (19) 式中： n 为采样分辨率， {y}_{i} 为真实值， \hat{{y}_{i}} 为预测值。通过最小化 \mathrm{M}\mathrm{S}\mathrm{E} 损失函数，使模型的预测结果尽可能接近真实的时均流场。
选用Adam优化器，结合Adagrad 和 Adadelta 两种优化算法的优点，自适应地调整学习率。为了防止过拟合，训练过程中引入了L2正则化与Dropout策略。模型的训练还结合了学习率调度机制和早停（early stopping）策略，以确保训练过程的稳定性和收敛速度。
4. 仿真与分析
本研究基于深度学习框架 TensorFlow 的 Keras 库构建了预测网络模型，并在 RTX
3090 GPU 上进行了加速训练，训练时间约为20 min。训练完成后，模型对测试集进行了预测，3组测试算例的预测结果如图13～图15和表5所示。![]()
图 13 时均流场预测结果与CFD结果对比Figure 13. Comparison of predicted mean flow fields with CFD results![]()
图 14 表面压力分布预测结果与CFD计算结果对比Figure 14. Comparison of predicted surface pressure distributions with CFD results![]()
图 15 三分力系数预测结果与CFD计算结果对比Figure 15. Comparison of predicted static force coefficients with CFD results表 5 三分力系数预测结果与CFD计算结果误差对比Table 5. Relative error of predicted static force coefficients三分力系数 平均相对误差（%） 均值 Shapes = 2 Shapes = 3 Shapes = 4 Shapes = 5 Shapes = 6 Shapes = 7 Size = 0.2, Vertices = 3～5 3.084 5.653 2.761 2.984 4.443 2.819 3.624 Size = 0.2, Vertices = 6～7 3.118 5.670 8.990 1.084 3.300 3.376 4.256 Size = 0.3, Vertices = 3～5 2.690 4.127 4.208 3.010 3.509 Size = 0.3, Vertices = 6～7 1.191 5.670 5.191 4.495 4.137 Size = 0.4, Vertices = 3～5 3.667 3.296 4.285 3.749 Size = 0.4, Vertices = 6～7 3.893 3.010 4.076 3.660 Size = 0.5, Vertices = 3～5 6.250 3.118 4.924 Size = 0.5, Vertices = 6～7 2.466 4.869 3.668 4.1 时均流场预测结果
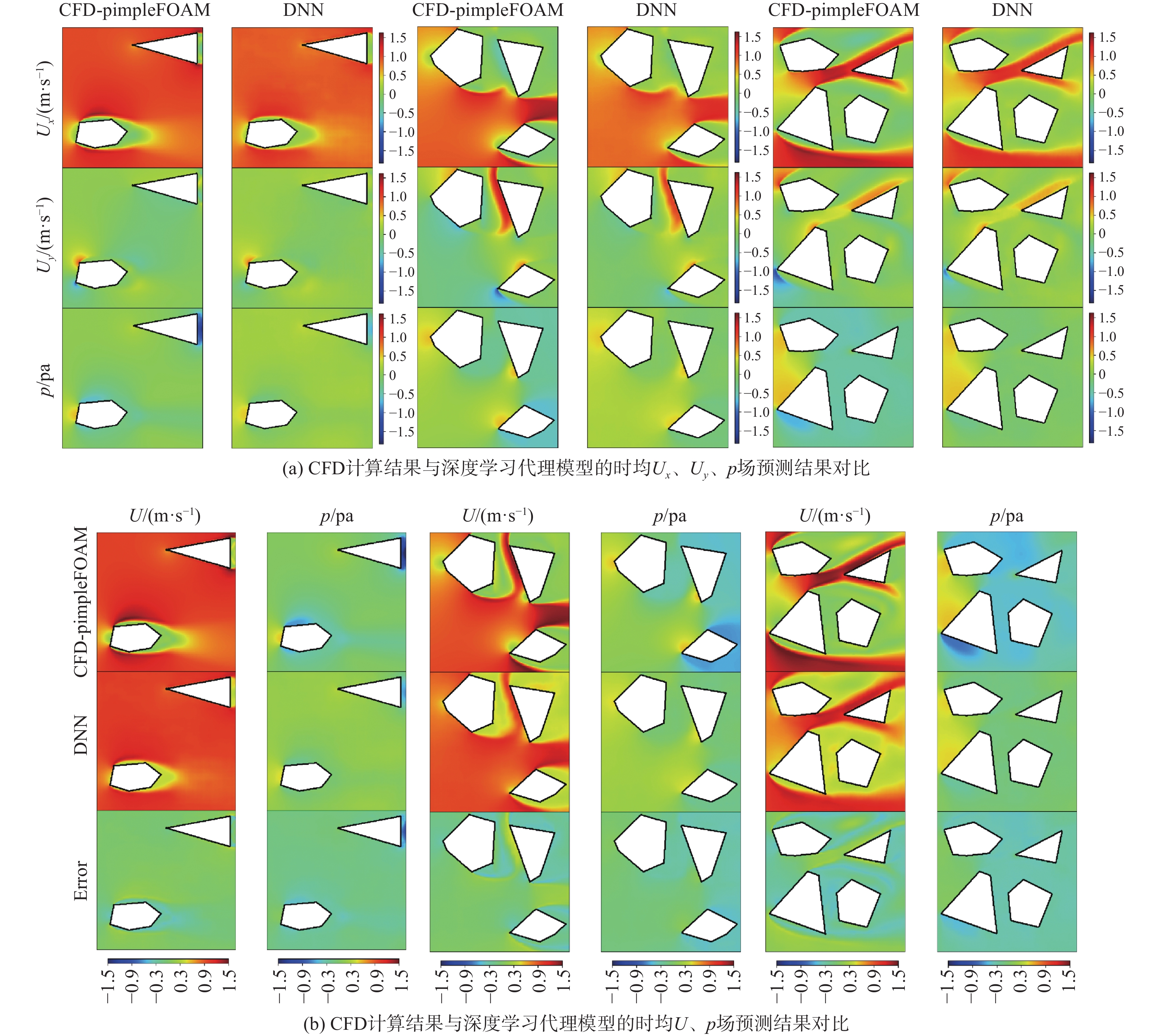
图13展示了模型对时均流场的预测结果与CFD计算结果的对比。从图中可知，本研究所提出的深度学习模型（deep neural network, DNN）在处理不同钝体断面流场时，得到的流场分布趋势与传统数值模拟方法的结果几乎完全一致；尽管本研究预测结果在尾流区域出现了轻微的速度过冲现象，但最大相对误差仅为3.7%。这表明本研究模型在处理多种几何形状时，能够较为精确地捕捉不同组合断面气动外形的复杂特征，表现出了较高的预测精度。
4.2 表面压力分布预测
图14展示了模型预测的表面压力分布结果与CFD计算结果的对比。由图可知，模型在表面压力预测上也表现出较高的精度，迎风面预测误差集中在±0.2%以内，背风面预测误差因流动分离影响增至±0.4%，预测结果与CFD计算的压力分布曲线之间的最大相对误差为0.35%。
总体而言，模型表现出较高的适应性和鲁棒性。预测结果与CFD计算结果的表面压力分布曲线一致性较好，背风面误差较大的原因主要在于气动外形与气动性能之间的映射关系高度非线性，尤其是在流动分离区域，微小的几何变化可能会导致显著的性能差异，模型未能有效捕捉局部压力变化趋势。
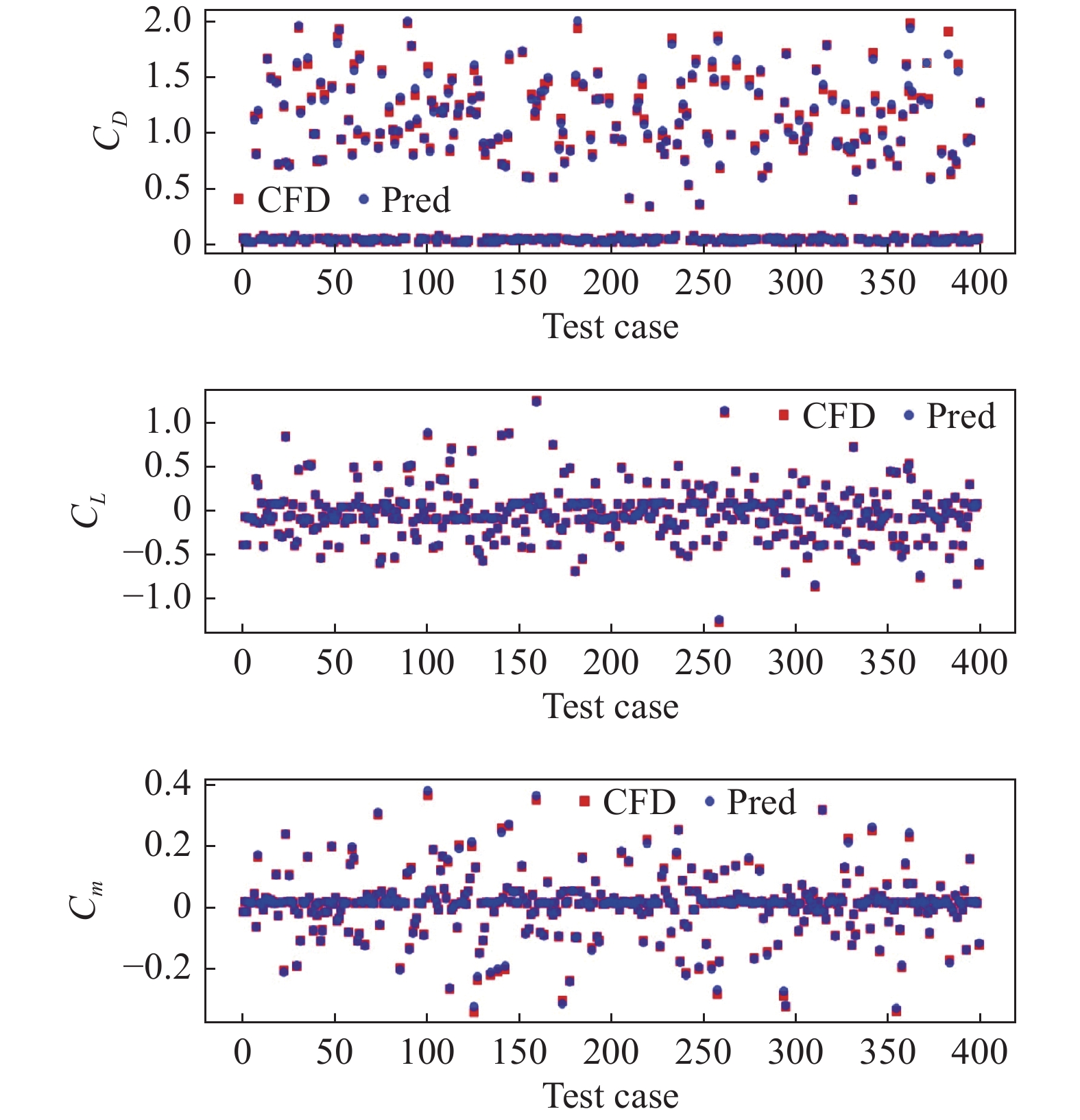
4.3 三分力系数与CFD数值模拟结果对比
图15展示了模型预测的三分力系数结果与CFD计算结果的对比。通过对比可知，模型在预测升力系数、阻力系数和升力矩系数时与CFD数值模拟结果高度一致，最大相对误差分别为4.19%、3.54%和6.25%。表5进一步以输入断面基础参数分类对比了不同组合断面的三分力系数预测结果误差。可以看出深度学习模型不仅能够准确预测结构绕流流场和表面压力分布，还能够高效地捕捉到不同组合断面的气动特性，准确预测三分力系数等气动参数。
此外，模型还大大提高了预测效率，单工况的计算时间从2 h缩短至0.2 s，同时硬件成本降低了94%。
5. 结 论
本研究提出了一种融合残差注意力机制模块的深度学习代理模型，能够高效预测定常风条件下钝体二维组合断面绕流流场及静力三分力系数。主要结论如下：
1） 提出了钝体组合断面一致化形状表达。该方法将钝体断面气动外形的局部动力学信息转化为场表示，适用于多形状组合的复杂结构断面，为气动选型提供了高效且灵活的解决方案。
2） 构建了基于深度学习的智能预测模型，精准捕捉复杂流动特征，时均流场最大相对误差保持在3.7%以内，表面压力分布最大相对误差保持在0.35%，三分力系数最大相对误差为6.25%，满足高精度要求；且计算效率大幅提升，与传统CFD数值模拟方法相比，智能预测模型在计算效率上提高了4个数量级，大幅提升了气动选型与优化效率。
尽管模型在流动分离区的预测精度仍有待提高，但是该模型能够在设计初期快速评估不同外形的气动性能，显著缩短设计周期。未来可望进一步通过引入物理约束损失函数和多尺度特征融合机制，提升对气动外形特征的捕捉能力，并扩展应用于变风速、变雷诺数以及三维流动等更复杂的工况[24-26]。
-
![]()
图 13 时均流场预测结果与CFD结果对比
Figure 13. Comparison of predicted mean flow fields with CFD results
![]()
图 14 表面压力分布预测结果与CFD计算结果对比
Figure 14. Comparison of predicted surface pressure distributions with CFD results
![]()
图 15 三分力系数预测结果与CFD计算结果对比
Figure 15. Comparison of predicted static force coefficients with CFD results
表 1 网格无关性验证
Table 1 Grid independence study
Cells/104 Refinement level Boundary layer/layers C_D C_L C_m {\mathrm{error}}_{CD}/% {\mathrm{error}}_{CL} /% {\mathrm{error}}_{Cm} /% Álvarez A J[23] — — — 0.140 –0.234 0.267 — — — Grid 1 45.8 4 0 0.140 –0.254 0.382 0 8.55 43.07 Grid 2 69.3 5 0 0.154 –0.246 0.360 10.00 5.13 34.83 Grid 3 126.9 6 0 0.154 –0.245 0.234 10.00 4.70 12.36 Grid 4 74.8 5 2 0.146 –0.237 0.290 4.29 1.28 8.61 Grid 5 77.8 5 3 0.145 –0.236 0.264 3.57 0.85 1.12 Grid 6 85.2 5 4 0.144 –0.236 0.265 2.86 0.85 0.75 
下载: 导出CSV
表 2 气动外形的主要参数特征
Table 2 Main characteristic parameters of aerodynamic shapes
parameter Shapes Size Vertices Pixels/px min 2 0.2 3 256 max 6 0.5 7 256 注：表中Shapes表示组合断面中形状的个数；Size表示限制单个断面最大尺寸，m；Vertices表示组合断面单个形状的边数；Pixels代表采样的分辨率，像素（px），每个像素点pij的坐标通过–0.5–1/256+1/256i和–0.5–1/256+1/256j获得，其中i、j的取值范围均为[0,256]。
下载: 导出CSV
表 3 超参数优化区间
Table 3 Hyperparameter optimization space
Parameters Range Setting Filter [8,16,32,64] 32 Kernel [3×3, 7×7] 7×7 Lr [1×10–2, 1×10–3, 5×10–3] 1×10–2 注：表中Filter表示首层隐藏层通道数量；Kernel表示卷积注意力模块的卷积核尺寸；Lr表示初始学习率。
下载: 导出CSV
表 4 神经网络架构及参数
Table 4 Neural network structure and parameters
Encoder-Decoder Layer ResBlock CBAM Input Shape Output Shape Param downsampling Conv2D-1 True [1,256,256,3] [1,128,128,32] 896 downsampling Conv2D-2 True True [1,128,128,32] [1,64,64,64] 18496 downsampling Conv2D-3 True True [1,64,64,64] [1,32,32,128] 73856 downsampling Conv2D-4 True True [1,32,32,128] [1,16,16,256] 295168 downsampling Conv2D-5 True True [1,16,16,256] [1,8,8,512] 1179648 upsampling Conv2DTranspose-1 True [1,8,8,512] [1,16,16,256] 1179648 upsampling Conv2DTranspose-2 True [1,16,16,256] [1,32,32,128] 295168 upsampling Conv2DTranspose-3 True [1,32,32,128] [1,64,64,64] 73856 upsampling Conv2DTranspose-4 True [1,128,128,32] [1,128,128,32] 18496 upsampling Conv2DTranspose-5 [1,256,256,16] [1,256,256,16] 4624 Conv2D-6 [1,256,256,16] [1,256,256,3] 435 注：表中“Encoder-Decoder”代表编码器-解码器架构类别；“Layer”为网络层名称；“ResBlock”代表是否使用残差块（True为使用）；“CBAM”代表是否使用卷积块注意力模块（True为使用）；“Input Shape”为各层输入数据的形状，依次代表样本数量、高度维度、宽度维度和通道数；“Output Shape”为各层输出数据形状，依次代表样本数量、高度维度、宽度维度和通道数；“Param”为该层的参数量。
下载: 导出CSV
表 5 三分力系数预测结果与CFD计算结果误差对比
Table 5 Relative error of predicted static force coefficients
三分力系数 平均相对误差（%） 均值 Shapes = 2 Shapes = 3 Shapes = 4 Shapes = 5 Shapes = 6 Shapes = 7 Size = 0.2, Vertices = 3～5 3.084 5.653 2.761 2.984 4.443 2.819 3.624 Size = 0.2, Vertices = 6～7 3.118 5.670 8.990 1.084 3.300 3.376 4.256 Size = 0.3, Vertices = 3～5 2.690 4.127 4.208 3.010 3.509 Size = 0.3, Vertices = 6～7 1.191 5.670 5.191 4.495 4.137 Size = 0.4, Vertices = 3～5 3.667 3.296 4.285 3.749 Size = 0.4, Vertices = 6～7 3.893 3.010 4.076 3.660 Size = 0.5, Vertices = 3～5 6.250 3.118 4.924 Size = 0.5, Vertices = 6～7 2.466 4.869 3.668
下载: 导出CSV
-
[1] 谢壮宁, 顾明. 任意排列双柱体的风致干扰效应[J]. 土木工程学报, 2005, 38(10): 32−38. doi: 10.3321/j.issn:1000-131X.2005.10.006 XIE Z N, GU M. Wind-induced interference effects of arbitrary arrangement of twin cylindrical bodies[J]. Journal of Civil Engineering, 2005, 38(10): 32−38 (in Chinese). doi: 10.3321/j.issn:1000-131X.2005.10.006
[2] KIM Y C, JUN K D, TAMURA Y. Wind-induced coupled motion of tall buildings with varying square plan with height[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(5): 638−650. doi: 10.1016/j.jweia.2011.03.004
[3] HE X H, LI H, WANG H F, et al. Effects of geometrical parameters on the aerodynamic characteristics of a streamlined flat box girder[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2017, 170: 56−67. doi: 10.1016/j.jweia.2017.08.009
[4] 胡传新, 周志勇, 孙强. 主梁断面形式对大跨斜拉桥风致稳定性的影响研究[J]. 桥梁建设, 2018, 48(6): 53−57. doi: 10.3969/j.issn.1003-4722.2018.06.010 HU C X, ZHOU Z Y, SUN Q. Effects of bridge decks on stability of long-span cable-stayed bridge[J]. Bridge Construction, 2018, 48(6): 53−57(in Chinese). doi: 10.3969/j.issn.1003-4722.2018.06.010
[5] 吴倩云, 孙亚松, 刘小兵. 并列双方柱气动特性的干扰效应研究[J]. 工程力学, 2020, 37(S1): 265−269. doi: 10.6052/j.issn.1000-4750.2019.04.S007 WU Q Y, SUN Y S, LIU X B. Study on interference effect of aerodynamic characteristics of two parallel columns[J]. Engineering Mechanics, 2020, 37(S1): 265−269 (in Chinese). doi: 10.6052/j.issn.1000-4750.2019.04.S007
[6] 杨晶, 许福友, 曾冬雷. 宽高比为 10 的矩形断面气动特性试验研究[J]. 振动与冲击, 2020. YANG J, XU F Y, ZENG D L. Experimental study on the aerodynamic characteristics of a rectangular cross-section with a width-to-height ratio of 10[J]. Vibration and Shock, 2020 (in Chinese).
[7] MADSEN J I, SHYY W, HAFTKA R T. Response surface techniques for diffuser shape optimization[J]. AIAA Journal, 2000, 38: 1512−1518. doi: 10.2514/3.14576
[8] 高宇琦, 王浩, 徐梓栋, 等. 大跨度高铁连续梁桥箱梁断面静力三分力系数的数值模拟[J]. 南京工业大学学报(自然科学版), 2020, 42(3): 358−365. GAO Y Q, WANG H, XU Z D, et al. Numerical simulation of static tri-component coefficients of girder sections of a long-span high-speed railway continuous beam bridge[J]. Journal of Nanjing Tech University (Natural Science Edition), 2020, 42(3): 358−365(in Chinese).
[9] 左云. 不同梁宽的10∶1宽高比边主梁叠合梁气动特性研究[J]. 四川建筑, 2024, 44(2): 182−185. doi: 10.3969/j.issn.1007-8983.2024.02.062 ZUO Y. Study on aerodynamic characteristics of composite beams with 10∶1 aspect-to-height ratio of side girders with different Liang Kuan[J]. Sichuan Architecture, 2024, 44(2): 182−185 (in Chinese). doi: 10.3969/j.issn.1007-8983.2024.02.062
[10] CELIK I, KLEIN M, FREITAG M, et al. Assessment measures for URANS/DES/LES: an overview with applications[J]. Journal of Turbulence, 2006, 7(48): 48. doi: 10.1080/14685240600794379
[11] 陈晓春, 王元. 绕钝体分离流动的非定常数值模拟研究[J]. 空气动力学学报, 2007, 25(4): 513−520. doi: 10.3969/j.issn.0258-1825.2007.04.019 CHEN X C, WANG Y. The unsteady numerical simulation of separated flow around bluff bodies[J]. Acta Aerodynamica Sinica, 2007, 25(4): 513−520(in Chinese). doi: 10.3969/j.issn.0258-1825.2007.04.019
[12] 陈海, 钱炜祺, 何磊. 基于深度学习的翼型气动系数预测[J]. 空气动力学学报, 2018, 36(2): 294−299. CHEN H, QIAN W Q, HE L. Aerodynamic coefficient prediction of airfoils based on deep learning[J]. Acta Aerodynamica Sinica, 2018, 36(2): 294−299 (in Chinese).
[13] MIYANAWALA T P, JAIMAN R K. A novel deep learning method for the predictions of current forces on bluff bodies[C]. ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering. Madrid, Spain, 2018. doi: 10.1115/OMAE2018-78338
[14] GUO X X, LI W, IORIO F. Convolutional neural networks for steady flow approximation[C]. 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco California USA. New York: ACM, 2016: 481-490. doi: 10.1145/2939672.2939738
[15] ABBAS T, KAVRAKOV I, MORGENTHAL G, et al. Prediction of aeroelastic response of bridge decks using artificial neural networks[J]. Computers & Structures, 2020, 231: 106198. doi: 10.1016/j.compstruc.2020.106198
[16] LI K, LI H, LI S P, et al. Fully convolutional neural network prediction method for aerostatic performance of bluff bodies based on consistent shape description[J]. Applied Sciences, 2022, 12(6): 3147. doi: 10.3390/app12063147
[17] RIBEIRO M D, REHMAN A, AHMED S, et al. DeepCFD: Efficient steady-state laminar flow approximation with deep convolutional neural networks[EB/OL]. 2020: 2004.08826. https://arxiv.org/abs/2004.08826v3.
[18] LIN P F, YOU C Y, WANG Q L, et al. Deep learning-based fast prediction of flow field around multiple bluff bodies[J]. Advances in Wind Engineering, 2024, 1(2): 100020. doi: 10.1016/j.awe.2024.100020
[19] BERNARDINI E, SPENCE S M J, WEI D, et al. Aerodynamic shape optimization of civil structures: A CFD-enabled Kriging-based approach[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 144: 154−164. doi: 10.1016/j.jweia.2015.03.011
[20] TOMPSON J, SCHLACHTER K, SPRECHMANN P, et al. Accelerating eulerian fluid simulation with convolutional networks[EB/OL]. 2016: 1607.03597. https://arxiv.org/abs/1607.03597v7.
[21] CHEN D L, GAO X, XU C F, et al. FlowGAN: A conditional generative adversarial network for flow prediction in various conditions[C]. Proc of the 2020 IEEE 32nd International Conference on Tools with Artificial Intelligence (ICTAI), Baltimore, MD, USA. IEEE, 2020: 315-322. doi: 10.1109/ictai50040.2020.00057
[22] WOO S, PARK J, LEE J Y, et al. CBAM: Convolutional block attention module[C]. Computer Vision-ECCV 2018. Cham: Springer International Publishing, 2018: 3-19. doi: 10.1007/978-3-030-01234-2_1
[23] A J Á, NIETO F, KWOK K C S, et al. Aerodynamic performance of twin-box decks: A parametric study on gap width effects based on validated 2D URANS simulations[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 182: 202−221. doi: 10.1016/j.jweia.2018.09.004
[24] 陈冰雁, 刘传振, 白鹏, 等. 使用深度残差网络的乘波体气动性能预测[J]. 空气动力学学报, 2019, 37(3): 505−509. CHEN B Y, LIU C Z, BAI P, et al. Aerodynamic prediction for waveriders using deep residual learning[J]. Acta Aerodynamica Sinica, 2019, 37(3): 505−509 (in Chinese).
[25] SEKAR V, ZHANG M Q, SHU C, et al. Inverse design of airfoil using a deep convolutional neural network[J]. AIAA Journal, 2019, 57(3): 993−1003. doi: 10.2514/1.J057894
[26] 赵天铭, 柳阳威, 唐雨萌. 基于机器学习的压气机叶型优化设计[J]. 工程热物理学报, 2023, 44(4): 914−921. ZHAO T M, LIU Y W, TANG Y M. Optimization of compressor blade based on machine learning[J]. Journal of Engineering Thermophysics, 2023, 44(4): 914−921 (in Chinese).
计量
- 文章访问数: 1
- HTML全文浏览量: 0
- PDF下载量: 1
