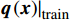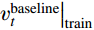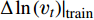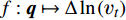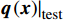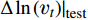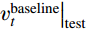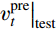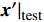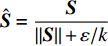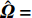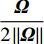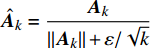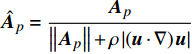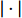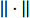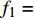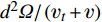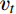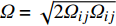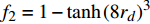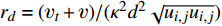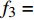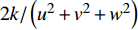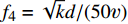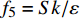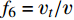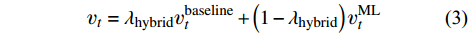Application of machine learning assisted turbulence modeling in flow separation prediction
-
摘要: 数据驱动湍流建模是近年来发展的提高雷诺平均N-S方程预测精度的有效手段,通过机器学习算法能够从高置信度数据中自动提取特征,建立准确的从平均流动特征到雷诺应力的预测模型。针对高雷诺数下积冰翼型绕流这一类典型的复杂流动分离问题,基于此前研究者提出的机器学习预测框架,从输入输出特征选择和翼型绕流中数据分布特性两个方面出发,对机器学习预测结果的光滑性和准确性进行改善。提出了基于雷诺应力张量分析和流动特征辨识的输入特征选择准则;提出了局部区域建模方法以及基准模型和机器学习预测模型混合的代入计算方法。将改进方法应用于积冰翼型绕流问题之中,结果表明改进的方法能够准确给出训练集和预测集上的雷诺应力结果,并且代入平均流计算可以得到和真实分布更加接近的流动和机翼表面压力分布。Abstract: Data-driven turbulence modeling has been considered as an effective method for improving the prediction accuracy of the Reynolds-averaged Navier-Stokes equations. By using machine learning algorithms such as the artificial neural network, features can be automatically extracted from high-fidelity data, and accurate prediction models from the mean flow characteristics to the Reynolds stress can be established. In this study, focused on the ice-accretion airfoil with the typical complex flow separation phenomenon under high Reynolds numbers, efforts are made in two aspects, i.e., the input and output feature selection and the data distribution characteristics of flow around an airfoil, to improve the smoothness and accuracy of the machine learning assisted prediction results. An input feature selection criterion based on the Reynolds stress tensor analysis and the flow characteristics identification is proposed, and a zonal modeling method together with a hybrid approach of the benchmark model and the machine learning assisted prediction model is also proposed. Results obtained from the improved method show that the Reynolds stress on both the training dataset and the prediction dataset can be accurately predicted, and the flow separation and pressure distribution on the airfoil agree well with the real situation.
-
0. 引 言
了解湍流结构的形成和演化机理从而准确预测湍流在现代工程问题中具有重要意义。目前受限于计算机技术的发展,直接数值模拟(Direct Numerical Simulation, DNS)或大涡模拟(Large Eddy Simulation, LES)等高精度数值方法仍然难以用于解决实际工程问题,雷诺平均N-S方程(RANS)仍然是气动设计中最常用的数值模拟方法。然而,许多复杂的流动现象例如旋流、强压力梯度流动、流线大曲率问题等,使用RANS方法无法给出符合工程设计精度要求的结果[1]。以飞机飞行中的流动分离问题为例,大迎角下失速、激波/边界层干扰引起的分离以及机翼表面积冰后升阻力性能的恶化都对飞行安全有着决定性的影响。然而对于RANS方法,研究人员比较了几种常用的湍流模型,发现它们都不能准确预测翼型上表面由于强逆压梯度而导致的流动分离[2]。对于RANS方法的计算误差,研究者一致认为主要来自所预测的雷诺应力的差异,即对于雷诺应力的建模误差。要改善预测效果,就要开发更准确的雷诺应力预测模型,即找到准确的雷诺应力与平均流动之间的映射关系[3-4]。
最早出现并且至今依然经常使用的雷诺应力封闭方法是基于线性涡黏性假设的湍流模型(Linear Eddy Viscosity Model, LEVM),它假设雷诺应力和平均流应变率成正比,并基于经验关联式或求解控制方程来确定两者的比例系数,即涡黏性。基于LEVM的湍流模型具有较好的计算鲁棒性,计算复杂问题时间成本较低,对于大部分边界层附着流动模拟效果较好,但是由于忽略了流线曲率的影响以及雷诺应力的实际各向异性特性,LEVM无法预测复杂的流动,例如方管流动中的二次流[5]和周期山流动中的分离区计算[6]。为了克服LEVM的局限性,研究者提出了非线性涡黏性模式和直接对雷诺应力进行建模的雷诺应力模式。这些改进的模型在某些复杂流动中可以提高预测精度。然而,非线性涡黏模型中额外添加的项和新增系数可能随流动问题变化且十分敏感,而雷诺应力模式则提高了计算成本,并且计算的鲁棒性较差[7]。综上所述,目前仍未出现一种既能给出不同类型复杂流动的精确结果,又能保持鲁棒性和节省成本的湍流计算模型,而此问题对于传统湍流建模框架难以彻底解决。
几十年的湍流研究中产生了大量的高置信度湍流数据,包括DNS和LES的数值计算结果以及实验观测结果。与此同时,随着高效统计推断算法和机器学习技术的发展,应用这些数据辅助湍流建模成为可能,这种框架被称为数据驱动建模,数据驱动方法目前的发展思路可以归纳为以下三类[8-9]:1)基于统计方法对RANS方法中的湍流模型不确定度进行评估。这种方法旨在对雷诺应力张量中的不确定性[10-11]进行量化,并通过统计推断方法识别流场中不确定度高的区域[12],从而有助于约束不确定性并明确RANS预测差异的具体来源。2)基于湍流数据推断湍流模型方程中待标定系数和生成、耗散项相对大小。这种方法选择对于湍流计算有关键影响的关注量(Quantities of Interests, QoIs)作为推断变量,可以是模型系数[13]或湍流模式控制方程[14-15]中的项(其初始值通常称为先验结果)。然后将这些选定的变量视为全流动分布的随机场,并根据给定的高置信度数据(如表面压力分布[15]或观测位置处的速度值[16])推断出最大化所选目标。如果选取的关注量合理,则使用修正后的关注量计算的流动结果(称为后验结果)将与目标吻合程度较高。3)用机器学习对湍流模型的预测结果直接进行修正或替代湍流模型进行雷诺应力的预测。这种方法的目的是建立平均流动特征和雷诺应力特征之间的映射。通过与大数据相结合,机器学习方法可以在不需要人为给出大量先验知识的前提下,提取多层次特征并给出回归或分类结果,这种强大的特征提取和回归能力使其适合于构建湍流模式的映射。在上述三种方法中,前两种方法不能产生预测模型,即无法用于改善训练和推断过程中没有出现过的算例数据集,而基于大数据训练的机器学习模型则可以被推广到具有相同类型的流动现象和流动结构的问题之中。机器学习模型的这种泛化能力使其更具工程应用价值,有助于降低进行实验或DNS计算的成本。因此,本研究采取第三种研究思路,即使用机器学习的方法来改进RANS模型的预测结果。
近年来基于机器学习的湍流建模研究得到了广泛的关注。其中对于训练目标量的选择反映了研究者对湍流预测误差的主要来源的认识以及应当如何处理的看法的不同,据此可以对相关研究进行分类。
第一种观点是以某一原始湍流模型为基准,通过修改模型方程中的某些项的相对大小来实现改进。Tracey等[17]利用机器学习对S-A模型中的源项进行重构,验证了该方法的可行性。Zhu等[18]直接以S-A模型计算的涡黏性为目标,建立人工神经网络。用网络代替原模型,提高了计算效率,降低了对网格密度的依赖性。以上为重现基准模型结果的工作,而如果目标是改进原始湍流模型在复杂问题中的效果,则应首先使用贝叶斯反演方法来推断修改后的源项,然后使用机器学习方法进行训练[15,19-20]。在这些研究中,研究者通过在湍流模型方程的生成项或耗散项上乘上一个全场变化的乘子实现对模型方程和平均方程的修正。由于这种方法通过输运方程来影响雷诺应力,因此更容易达到修正雷诺应力场的光滑性要求。然而,基准湍流模型使用的涡黏性假设限制了雷诺应力的各向异性,无论如何改变幅值,其雷诺应力主方向永远和应变率张量一致,因此目前的理论最优结果与真实雷诺应力仍然存在一定的差异。
第二种观点认为应选择整个雷诺应力作为训练目标。在Ling的工作[21]中,雷诺应力被表示为由平均流的应变率张量和旋转率张量构成的10个整基的线性组合。神经网络的输出变量是组合的各项系数,然后与相应的张量基相结合,组合出雷诺应力各向异性张量。这种类似非线性涡黏模型的想法启发了后来的一些研究[22]。除线性组合外,另一种对雷诺应力的表示方法是特征值分解方法。由于雷诺应力为对称二阶张量,特征值分解将给出一组实特征值和相互正交的特征向量,其中特征向量可以进一步用欧拉角[23]或四元数[24]来描述。对真实雷诺应力和RANS预测的雷诺应力进行分解,得到各特征的差量场,并以此作为机器学习的目标。
综合对比两种方法,以某个基准湍流模型结果为基础进行修正的方法待修正变量数量少,预测难度较低,但无法预测完整的雷诺应力特征;直接对雷诺应力进行表示和学习理论上能够最大程度再现真实结果,但待预测量变多,同时由于预测量直接对平均方程产生影响,也带来了光滑性的问题。
课题组此前基于周期山算例进行了机器学习辅助湍流建模的应用,改进后的框架在预测结果光滑性和精度上有所提升[25]。本文将基于此前研究,研究将此框架应用于积冰翼型的复杂绕流问题这一类工程实际问题里典型且关键的分离流动中的可能性。研究主要关注在建立机器学习预测框架过程中的输入量/输出量特征选择问题,外流绕流问题中数据分布不均匀带来的模型预测困难。文中提出了输入输出特征的选择准则,同时针对翼型流场进行了局部区域建模,验证了局部冻结的可行性,并将方法应用于典型积冰翼型的流动计算,提高了原始湍流模型的预测精度。
1. 研究方法
1.1 机器学习辅助湍流建模框架
首先对本文中所使用的机器学习辅助湍流建模的框架进行阐述。三维可压缩流动的RANS方程组如式(1)所示:
∂ρ∂t+∇⋅(ρu)=0∂∂t(ρu)+∇⋅(ρuu)=ρf+∇⋅T∂∂t(ρe)+∇⋅(ρeu)=∇⋅(T⋅u)+ρf⋅uT=−pI+[λ(∇⋅u)I+μ(∇u+u∇)]+τ (1) 其中,ρ、u、f、e、p、λ和μ分别为雷诺平均后的密度、速度、体积力、比总能、压力、体积黏性和分子黏性。T代表总应力张量,包括压力、分子黏性应力和由于雷诺平均而产生的雷诺应力τ。在传统湍流建模思路中,雷诺应力是由湍流模型方程确定的。当RANS方程和湍流模型方程均收敛时,求解过程结束。而机器学习在湍流建模中的作用是能够在给定一系列输入特征的情况下给出雷诺应力的直接或间接预测结果,即提供一个有预测能力的回归函数。要建立此回归函数,需要基于大量的已存在的高置信度数据,这个过程称为机器学习的训练过程。在训练完成之后,该函数则可以用于预测新的流动过程,称为测试过程,体现了机器学习模型在未知问题上的泛化能力。预测目标的选择、输入输出特征和机器学习算法对预测性能都有决定性的影响。
预测目标的选择随着学习真值类型的变化而变化。本文关注的应用场景为高雷诺数下飞行器实际飞行过程中的典型分离流动问题,而此方面高置信度DNS和LES模拟结果较为缺乏,本文研究中所选择的真值为课题组此前发展的SPF修正的三方程k-v2-ω(记为SPF k-v2-ω)湍流模式的计算结果[26]。该模型应用于高雷诺数下典型结冰翼型的流动预测结果和实验测量得到的力系数曲线、流场脉动量和平均量测量结果符合较好[26]。该三方程模式依然基于线性涡黏性模式框架,因此以该模式迭代收敛结果的涡黏性场作为真值,记为
νtruet 。在得到真值之后,将预测目标取为涡黏性真值场和基准湍流模式计算收敛结果(记为νbaselinet )的差量场,为保证预测的涡黏性场恒为正值,差量场的形式采用先取对数再做差的形式,如式(2)所示:Δln(νt)=ln(νtruet)−ln(νbaselinet) (2) 选取差量场作为目标能够更好地利用基准湍流模式对流动的先验结果,提供更合理的初始猜测,使得回归函数只关注差异显著的区域,从而降低训练难度。
为使得机器学习辅助湍流建模框架更符合湍流计算的合理性和可解释性,对于机器学习中的预测目标有以下两点要求:
1)预测目标应和其对应物理量具有同样自由度;
2)预测目标对于坐标旋转和平移应具有不变性。
可以看出,本文选取的
Δln(νt) 自由度为1,和涡黏性的自由度一致;另由于预测目标为标量场,因此自动满足对于坐标旋转和平移的不变性。因此以上两点要求得到满足。选取涡黏性的差量场作为目标,其输入量特征应来自于基准模式计算的结果,并且在代入平均方程计算时需要在迭代过程中保持冻结,直至平均方程残差重新收敛,即意味着在第二轮重新迭代开始之前只调用一次机器学习模型进行预测。
机器学习辅助的湍流建模框架整理如下,并如图1所示。
1)在训练集和测试集的算例上生成计算网格,并且计算基准湍流模式的结果;
2)从训练集的基准模型计算结果平均值x中构造出平均流输入特征
q(x)|train 并提取出基准涡黏性场νbaselinet|train ;3)获得待学习目标差量场
Δln(νt)|train ;4)根据训练集数据使用随机森林算法构建映射函数
f:q↦Δln(νt) ;5)将训练后的随机森林模型应用于测试集,基于测试集平均流输入特征
q(x)|test 给出Δln(νt)|test ,和测试集基准模型给出的νbaselinet|test 结合得到经过机器学习方法修正后的涡黏性场νpret|test ;6)将预测出的涡黏性场代入CFD求解器中并冻结,重新迭代RANS方程直至平均流重新收敛,得到修正后的平均场结果
x′|test ,求解结束。1.2 基于张量分析和物理特征分析的输入特征选择
根据1.1节的描述,本文中所使用的机器学习框架输入特征应当由基准湍流模型计算得到的平均流特征而构造出。而这些输入特征还应当满足以下三条基本原则:
1)完整性,即输入特征集应包括与雷诺应力分布相关的所有可能信息;
2)紧凑性,即应识别并删除输入特征集中的无效或冗余信息;
3)可实现性,即要求只要流动结构保持不变,输入特征集的变量在不同情况下(例如不同的参考坐标系或流向)应保持一致。
满足前两个原则有助于提高机器学习模型的性能,使其更具外推性和准确性;第三个原则保证了数据驱动模型能够具有和传统湍流模型一样的物理合理性。关于输入量特征的选取已有许多研究[27-28]。本文提出了两种分别基于张量分析和物理特征识别的选择准则,以往研究中出现的输入量均可以被分类入这两种角度,同时还可以在准则的指导下构造出新的有效特征并添加到输入集中。
1.2.1 基于雷诺应力表示的特征量选择
首先考虑通过寻找雷诺应力所依赖的张量或矢量,并构造一个完整的张量基来表示雷诺应力。非线性涡黏性假设就是一种典型的基于雷诺应力表示方法的湍流模式,其将雷诺应力假定为平均流应变率S和旋转率Ω的多项式组合。Pope[29]利用张量函数表示理论,推导出包含10个分量的整基,从而得到多项式的紧致形式。完整性基础保证了由S和Ω构成的每一个对称二阶偏张量都可以表示为这10个张量的线性组合。受此启发,Wu等[24]在此基础上进一步增加压力梯度Δp和湍动能梯度Δk,以补充强压力梯度和湍流强度非均匀分布的影响。为了方便表示,将这两个梯度转化为相应的反对称张量Ap和Ak。同样根据张量表示定理得到由此这四个张量组成的47个分量的整基。由于整基的分量都是张量,不能直接用作输入特征,进一步选择张量的第一不变量,即每个张量的迹作为输入特征。针对本文中的翼型绕流问题,首先从以上特征中去掉二维下为零以及绝对值相同的重复特征(此时剩余17个特征),另外由于结冰翼型网格较为复杂,难以实现较高的光滑性,因此进一步去掉剩余特征中对于网格光滑性十分敏感的部分高阶特征,最终剩余6个特征,如表1所示。表中符号说明如下:
ˆS=S‖ ,{\hat{ \varOmega }} = \dfrac{{{\varOmega }}}{{2\left\| {{\varOmega }} \right\|}} ,{{\hat{ A}}_k} = \dfrac{{{{{A}}_k}}}{{\left\| {{{{A}}_k}} \right\| + \varepsilon /\sqrt k }} ,{{\hat{ A}}_p} = \dfrac{{{{{A}}_p}}}{{\left\| {{{{A}}_p}} \right\| + \rho \left| {\left( {{{u}} \cdot \nabla } \right){{u}}} \right|}} ,其中,\left| {\; \cdot \;} \right| 表示向量范数,\left\| {\; \cdot \;} \right\| 表示Frobenius矩阵范数,变量ε是湍流耗散率,nsym和nanti表示在构造整基时中使用的对称/反对称张量的数量。表 1 基于雷诺应力表示选取的特征量Table 1. Input features selected based on the Reynolds stress representation(nsym, nanti) Feature No. Invariants (1, 0) q1 {{\hat{ S}}^2} (0, 1) q2, q3 {\hat{ A}}_p^2,\quad {\hat{ A}}_k^2 (1, 1) q4 {\hat{ A}}_k^2{\hat{ S}} (0, 2) q5 {{\hat{ A}}_p}{{\hat{ A}}_k} (1, 2) q6 {\hat{ A} }_p^2{{ \hat{ \varOmega} \hat {{S} } } } 1.2.2 基于流动辨识的特征量选择
由于输入特征完全基于基准计算平均场进行构建,当平均场真值和基准值差距较大时难以给出合理表示结果,为进一步补充输入特征引入第二种思路,即通过寻找或构造标志性变量用以定位和定量描述基准场和真值场之间较大的差异。与1.2.1节的表示方法相比,寻找识别差异的标记并将其作为输入更直接并且和预测目标相关性更高。除了标记功能外,所选特征还应具有明确的物理意义,以保证在具有相似流结构的流中具有相似的性能。一方面可以通过构造能够识别关键流动特征的准则量来实现,因为基准值和真值的差异往往出现在复杂的流动结构中。以所积冰型为明冰的翼型为例,冰后产生强烈分离形成流动分离泡并在机翼上再附,基准湍流模型预测的误差主要来自分离泡内剪切层、强逆压力梯度和旋流的预测,通过识别以上流动结构就可以找到待修正区域,在传统建模中也采用了这种思路。另一方面,可以构造出湍流相关物理量的相对大小比率来反映出基准模型对于关键流动现象的辨识程度,将其加入输入量就可以更好定位基准湍流模式的误差以及给出修正方向。综合两方面考虑,以及和上面相同的考虑特征光滑性对于网格光滑性的敏感程度之后,整理出如下所示的6个标量特征。
1)流动剪切层和旋涡流动的识别函数[14]:
{f_1} = {d^2}\varOmega /\left( {{\nu _t} + \nu } \right) ,其中d为到壁面的距离,{\nu _t} 为基准湍流模式预测的涡黏性,\varOmega = \sqrt {2{\varOmega _{ij}}{\varOmega _{ij}}} ;2)边界层识别函数(DDES使用的保护函数)[30]:
{f_{\rm{2}}} = 1 - \tanh \left( {{{ {8{r_d}} }}} \right)^3 ,其中{r_d} = {({{\nu _t} + \nu })}/({{{\kappa ^2}{d^2}\sqrt {{u_{i,j}}{u_{i,j}}} }} ) ;3)基准模式计算湍动能和平均流动能之比:
{f_{\rm{3}}} = 2k/\left( {{u^2} + {v^2} + {w^2}} \right) ;4)基于壁面距离的湍流雷诺数[31]:
{f_{\rm{4}}} = {{\sqrt k d}}/({{50\nu }} ) ;5)湍流时间尺度和平均流时间尺度之比:
{f_{\rm{5}}} = Sk/\varepsilon ;6)基准模式计算涡黏性和分子黏性之比:
{f_{\rm{6}}} = {\nu _t}/\nu 。综上所述,从平均流变量中构造出了12个标准化的不变量作为机器学习框架的输入特征。
1.3 针对翼型绕流问题的局部建模和代入计算
此前大部分机器学习辅助湍流建模框架的研究都以内流流动作为研究对象,内流和外流在关键流动结构上可能比较接近(例如周期山流动分离和结冰翼型后流动分离),但是在进行外流流动的模拟时为了保证远场边界条件对绕流物体附近流场的影响足够小,远场的特征长度需要是绕流物体特征长度的50~100倍。远离壁面的流动数据即使网格变疏,但仍然占据流场数据的一大部分,并且此部分流动数据由于没有受到过多扰动,大部分输入特征保持一致没有波动,预测的雷诺应力和真值区别也较小,因此对于机器学习模型的训练带来了不利影响。为解决这一问题,Zhu等[18]在全场重构S-A模型时,使用了分区建模的方法,根据到壁面距离对整个流场进行划分,不同区域分别训练。在此问题中,本文进一步考虑只针对机翼附近的区域进行训练,而其他区域依然使用基准湍流模式进行计算,区分于原来的分区域建模方法,本文的思路可以称为局部区域建模。和分区域建模对比,局部区域建模首先大大降低了机器学习模型训练的成本,因为远场并不需要进行训练;另外局部区域建模能够合理限制机器学习算法的影响区域,机器学习模型影响的范围基本被约束在壁面附近,对于复杂组合的流动问题,这种思路能够保证机器学习的误差不会影响到原本区别很小的区域造成额外的误差。
接下来从模型训练和代入计算角度详细说明局部区域建模的思路。进行局部区域建模从机器学习模型训练角度容易处理,本文根据预测目标量(差量场)在空间中的显著区域大小,确定了拆分的壁面距离范围,并按照所生成翼型结构网格的ijk指标范围进行了拆分,在机器学习模型的训练和预测中,均只使用该区域内的流动数据。
对于局部区域建模,将预测模型和CFD平均流计算过程耦合起来是一个重要问题。本文采用的基本思路是依然在全场计算湍流模型方程,当每一迭代步需要将涡黏性代入平均流方程中时,在指定需要冻结的区域的涡黏性场替换为冻结的值,其余部分代入湍流模式计算的结果。这种方法能够自由指定需要替换的区域而不必修改湍流模型方程的求解区域和相应的边界条件,容易在程序中实现;并且经过计算验证,在收敛的情况下平均场能够得到光滑的平均速度场。但是这种局部冻结的方法对CFD计算的收敛带来了挑战。由于冻结的涡黏性和基准湍流模型计算的涡黏性存在较大差异,导致在分区的边界上存在间断,验证计算中表明如果直接进行冻结会导致湍流模型方程在迭代过程中很快发散,并且无法通过调整CFL数或增加迭代步数来改善。
本文为解决局部区域冻结CFD计算容易发散的问题,采用了混合的思路:在局部冻结区域将读入的机器学习模型预测的涡黏性和基准湍流模式计算的涡黏性按照一定比例进行混合,混合系数记为λhybrid,如式(3)所示,当λhybrid为0时表示完全为冻结量,为1时则表示未代入全部为基准计算结果。
{\nu _t} = {\lambda _{{\rm{hybrid}}}}\nu _t^{{\rm{baseline}}} + \left( {1 - {\lambda _{{\rm{hybrid}}}}} \right)\nu _t^{{\rm{ML}}} (3) 在实际计算中,首先使用基准湍流模式计算出待修正构型的收敛结果,再采用如上的混合冻结方法计算若干步,之后再完全替换为冻结涡黏性,计算验证结果表明了这种处理能够有效地解决冻结区域内外初始差距过大带来的湍流模型方程发散的问题。
2. 数值方法验证
本部分内容将针对上面研究方法部分提到的全场和局部冻结涡黏性的计算方法进行验证,在此过程中暂不引入机器学习模型,直接使用真值进行计算,即获得当前方法能够得到的理论上限,考察方法的合理性。所选取的算例采用了带944冰型的GLC305翼型绕流问题[32](记为GLC305/944),模拟和实验中的来流马赫数为0.12,基于来流速度和翼型弦长的雷诺数为3.5×106,在本部分的验证工作中,选取迎角6°的工况作为研究对象,图2给出了所生成的结构网格,采用C型网格拓扑,翼型表面网格点282个(尾迹区网格点88个),垂直壁面的法向网格点97个,总计网格量为44 329;所选择的需要进行局部冻结的区域如红色框所示,冻结范围的确定目前根据对流动状态的观察结果确定,选取包括速度梯度、分离泡范围、涡黏性场变化等平均场特征明显、梯度较大的区域,该区域内总计网格量为20 952。本文使用适用于可压缩流动求解的开源程序CFL3D v6.7[33]求解流动,并且在原程序的基础之上添加了冻结全场/局部涡黏性以及进行涡黏性混合的功能。
首先使用SST模式和SPF k-v2-ω对该算例进行模拟,前者的结果将作为后续机器学习训练和预测中的基准结果,给出涡黏性的初始猜测以及组合出输入特征。后者的涡黏性结果将作为机器学习训练的标签值,并在预测集上作为真值和预测结果对比。图3(a、b)分别给出了SST和SPF k-v2-ω的平均速度计算结果。从图中可以看出,SST模式计算得到的分离泡分布在整个翼型上表面,而SPF k-v2-ω的计算结果和文献中的实验结果相近,分离泡在43%左右弦长处再附。两种模式计算结果的区别主要在于对冰角后的自由剪切层流动模拟的差异。文献[26]指出,SST模式由于基于湍流平衡假设,在自由剪切层中湍动能生成项始终和破坏项赋值相近,从而无法模拟出自由剪切层发展过程中高低速流动的充分混合,产生了更大的分离区,而SPF k-v2-ω模式通过设置自由剪切层标识函数,对原始三方程源项进行修改并设置阈值函数,最终得到了和实验更为符合的湍动能分布和生成耗散特性。
得到两种模式的计算结果之后,如1.3节所述进行两种冻结计算。首先将SPF k-v2-ω模式计算得到的整个计算域的涡黏性提取出来,并且代入SST模式的收敛计算结果进行续算,并直至重新收敛;第二种冻结计算是将如图2所示红色区域内的涡黏性进行冻结,并且采用在前55 000步迭代中进行混合(取λhybrid = 0.5),再全部冻结为读入的涡黏性进行重新计算直至流动收敛,两种迭代得到的平均速度云图(以迎角6°下的结果为例)结果如图3(c、d)所示,对应的升力系数的收敛曲线如图4所示。从收敛情况可以看出,局部冻结的开始阶段力系数的震荡较明显,但是混合方法保证了计算能够继续,经过一定步数迭代后替换为全冻结就可以保证流动收敛到合理的结果。从图3(b~d)对比可以看出,无论使用全场冻结还是局部冻结,最终得到的平均流场和SPF k-v2-ω的计算结果一致性很高,证明了当前方法的有效性和机器学习模型能够达到的理论上限足以实现对平均流动的正确修正。
此外,本文还针对所提出的涡黏性混合方法进行了进一步计算验证,以说明不同的混合系数对于计算的影响。同样,迎角6°算例,取混合系数Ratio分别为0 (相当于不进行混合)、0.25、0.50、0.75进行4次计算。所有计算均在使用基准SST湍流模型计算40 000步结果收敛之后,在其基础上进行续算得到。4个计算结果的升力系数结果如图5所示。当混合系数取0时,可以看到流动在达到收敛结果之前就计算发散;当采用了混合系数之后,在进行混合计算的40 000步至80 000步之间,计算均可收敛。而当80 000步以后,此时所有计算都结束混合并冻结为雷诺应力全量,混合系数为0.25和0.5的结果能够最终顺利收敛至同一结果,对应的升力系数为真值的升力系数,而混合系数0.75则在此过程中出现了计算发散,说明在混合计算阶段没有起到完全消除计算不稳定性的作用。以上计算结果说明,混合系数分别影响“原始计算-部分冻结”和“部分冻结-全部冻结”的两个过程,混合系数越小,第一个过程的震荡和发散的可能越大,反之则第二个过程震荡和发散的可能性更大。只要确保流动收敛之后,不同混合系数可以达到同样的计算结果。
3. 模型训练与预测结果
本文通过改变来流迎角构造出训练集和测试集,分别计算迎角为4°、5°、6°和7°四个工况,选取4°和6°的结果为训练集,5°和7°的结果为测试集。由于流动分离现象的变化随迎角增加具有一致性,因此迎角5°和7°相当于机器学习预测的内插和外推情况,可以更好地考察机器学习模型的泛化能力。
本文使用的机器学习算法为随机森林方法,基于Python平台的scikit-learn包进行程序实现[34]。随机森林方法基于一组经过训练的决策树,能够在进行回归或分类的同时给出每个输入特征在所有决策树中的重要性评价。模型超参数包括决策树的最大特征数和决策树数量,前者取为5,从而满足1 + log2n的关系式,其中n = 12为输入特征数量;后者取为300,和文献[25]保持一致。
为和本文提出的局部区域建模冻结的计算方法进行对比,建立两个随机森林模型,分别使用全场数据和局部数据进行训练和预测。训练在工作站上进行,CPU型号为Intel Xeon E5-2670,主频为2.30 GHz,内存为64 GB。两个模型训练过程的基本信息如表2所示。从对比可以看出,采用局部区域冻结能够极大降低训练成本,对于大数据量的情况下优势十分显著。
表 2 两个随机森林模型训练过程基本信息Table 2. Basic information for the training process using two random forest models冻结类型 训练集数据量 单核训练时长 全场冻结 88 658 7 h 40 min 局部冻结 41 904 25 min 机器学习的结果在作为训练集的迎角4°和6°上均和真值符合很好,为展现机器学习模型的泛化能力,下面集中于预测集上的结果,即迎角5°和7°。图6以迎角5°为例给出涡黏性对数差量场的真值和预测值的云图对比,其中图6(a)为真值,图6(b)为对全场涡黏性差量场进行训练和预测的结果,图6(c)则为针对局部涡黏性差量场进行建模的结果,因此并没有全场的结果。首先可以从涡黏性差量场的真值分析基准SST模式和作为真值的SPF k-v2-ω模式计算结果在平均场上的差别:在流动剪切层刚开始发展的位置降低了涡黏性,保证分离泡初始发展、高度等特征和真值更加符合,在翼型弦长30%以后相较于基准SST模式具有更高的涡黏性,保证流动在正确的位置附着。对比基于全场和局部数据训练模型可以看出,局部训练数据将范围约束在翼型附近之后,对于剪切层开始位置的拟合程度更高,而全场数据训练模型则没有完全反映出冰后的涡黏性分布趋势。
用预测出的对数差量场结合SST模式的涡黏性场重构出预测的涡黏性值,并且将涡黏性代入CFD求解器中进行冻结,直至平均流重新收敛。其中基于局部数据训练的模型,其冻结计算按照数值方法部分的说明进行混合计算,混合步长和系数均保持一致。图7分别展示了迎角5°和7°两个预测算例从流场中截取特定流向位置剖面的速度数据进行对比,黑色实线、红色实线和蓝色虚线分别为原始SST模式、作为真值的SPF k-v2-ω模式以及使用局部机器学习模型预测的结果。可以看出无论是内插还是外推结果,使用机器学习方法修正后的涡黏性代入计算的平均流效果能够和真值结果符合,分离泡的大小和再附位置都和真值十分接近。
进一步对比翼型表面的压力系数结果,如图8所示。可以看出压力系数也和真值符合程度很好。综上所述,机器学习应用于分离流动的平均流预测具有较好的拟合能力和泛化能力,能够切实改进预测效果。
4. 结 论
本文讨论了机器学习辅助湍流建模框架的建立,包括从输入量集合构建、特征选择和机器学习方法选择。针对将机器学习模型应用于外流流动这一场景,采用了仅针对流场部分区域进行建模的方式以及相应提升计算收敛性的雷诺应力混合计算方法。将这种方法和全场建模在时间成本和预测效果上进行了对比,结果表明局部建模方法降低了机器学习框架应用于复杂外流流动问题的时间成本,提高了训练效率和准确性,仅针对关键区域进行修正同样能够实现对于平均流动较好的修正效果。进一步工作将探讨以LES或DNS结果为真值情况下局部建模方法的效果。
-
表 1 基于雷诺应力表示选取的特征量
Table 1 Input features selected based on the Reynolds stress representation
(nsym, nanti) Feature No. Invariants (1, 0) q1 {{\hat{ S}}^2} (0, 1) q2, q3 {\hat{ A}}_p^2,\quad {\hat{ A}}_k^2 (1, 1) q4 {\hat{ A}}_k^2{\hat{ S}} (0, 2) q5 {{\hat{ A}}_p}{{\hat{ A}}_k} (1, 2) q6 {\hat{ A} }_p^2{{ \hat{ \varOmega} \hat {{S} } } } 表 2 两个随机森林模型训练过程基本信息
Table 2 Basic information for the training process using two random forest models
冻结类型 训练集数据量 单核训练时长 全场冻结 88 658 7 h 40 min 局部冻结 41 904 25 min -
[1] CRAFT T J, LAUNDER B E, SUGA K. Development and application of a cubic eddy-viscosity model of turbulence[J]. International Journal of Heat and Fluid Flow, 1996, 17(2): 108-115.DOI: 10.1016/0142-727X(95)00079-6[LinkOut]
[2] CELIC A, HIRSCHEL E H. Comparison of eddy-viscosity turbulence models in flows with adverse pressure gradient[J]. AIAA Journal, 2006, 44(10): 2156-2169.DOI: 10.2514/1.14902[LinkOut]
[3] SPALART P R. Philosophies and fallacies in turbulence modeling[J]. Progress in Aerospace Sciences, 2015, 74: 1-15.DOI: 10.1016/j.paerosci.2014.12.004[LinkOut]
[4] 佘振苏, 唐帆, 肖梦娟. 面向精准工程湍流模型的理论研究[J]. 空气动力学学报, 2019, 37(1): 1-18. doi: 10.7638/kqdlxxb-2018.0249 SHE Z S, TANG F, XIAO M. Structural ensemble dynamics theory for engineering turbulence models[J]. Acta Aerodynamica Sinica, 2019, 37(1): 1-18. (in Chinese)DOI: 10.7638/kqdlxxb-2018.0249[万方]
[5] SPEZIALE C G. On nonlinear K-l and K-ε models of turbulence[J]. Journal of Fluid Mechanics, 1987, 178: 459-475.DOI: 10.1017/s0022112087001319[LinkOut]
[6] BREUER M, PELLER N, RAPP C, et al. Flow over periodic hills - Numerical and experimental study in a wide range of Reynolds numbers[J]. Computers & Fluids, 2009, 38(2): 433-457.DOI: 10.1016/j.compfluid.2008.05.002[LinkOut]
[7] SPALART P R. Strategies for turbulence modelling and simulations[J]. International Journal of Heat and Fluid Flow, 2000, 21(3): 252-263.DOI: 10.1016/S0142-727X(00)00007-2[LinkOut]
[8] DURAISAMY K, IACCARINO G, XIAO H. Turbulence modeling in the age of data[J]. Annual Review of Fluid Mechanics, 2019, 51(1): 357-377.DOI: 10.1146/annurev-fluid-010518-040547[LinkOut]
[9] 张伟伟, 朱林阳, 刘溢浪, 等. 机器学习在湍流模型构建中的应用进展[J]. 空气动力学学报, 2019, 37(3): 444-454. doi: 10.7638/kqdlxxb-2019.0036 ZHANG W W, ZHU L Y, LIU Y L, et al. Progresses in the application of machine learning in turbulence modeling[J]. Acta Aerodynamica Sinica, 2019, 37(3): 444-454. (in Chinese)[万方] doi: 10.7638/kqdlxxb-2019.0036
[10] EMORY M, LARSSON J, IACCARINO G. Modeling of structural uncertainties in Reynolds-averaged Navier-Stokes closures[J]. Physics of Fluids, 2013, 25(11): 1155.
[11] XIAO H, WANG J X, GHANEM R G. A random matrix approach for quantifying model-form uncertainties in turbulence modeling[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 313: 941-965.DOI: 10.1016/j.cma.2016.10.025[LinkOut]
[12] LING J, TEMPLETON J. Evaluation of machine learning algorithms for prediction of regions of high Reynolds averaged Navier Stokes uncertainty[J]. Physics of Fluids, 2015, 27(8): 085103.DOI: 10.1063/1.4927765[LinkOut]
[13] EDELING W N, CINNELLA P, DWIGHT R P. Predictive RANS simulations via Bayesian model-scenario averaging[J]. Journal of Computational Physics, 2014, 275: 65-91. doi: 10.1016/j.jcp.2014.06.052[LinkOut]
[14] DURAISAMY K, ZHANG Z J, SINGH A P. New approaches in turbulence and transition modeling using data-driven techniques[C]// 53rd AIAA Aerospace Sciences Meeting, Kissimmee, Florida. Reston, Virginia: AIAA, 2015. doi: 10.2514/6.2015-1284
[15] SINGH A P, MEDIDA S, DURAISAMY K. Machine-learning-augmented predictive modeling of turbulent separated flows over airfoils[J]. AIAA Journal, 2017, 55(7): 2215-2227.DOI: 10.2514/1.J055595[LinkOut]
[16] XIAO H, WU J L, WANG J X, et al. Quantifying and reducing model-form uncertainties in Reynolds-averaged Navier-Stokes simulations: a data-driven, physics-informed Bayesian approach[J]. Journal of Computational Physics, 2016, 324: 115-136. doi: 10.1016/j.jcp.2016.07.038[LinkOut]
[17] TRACEY B D, DURAISAMY K, ALONSO J J. A machine learning strategy to assist turbulence model development[C]// 53rd AIAA Aerospace Sciences Meeting, Kissimmee, Florida. Reston, Virginia: AIAA, 2015. doi: 10.2514/6.2015-1287
[18] ZHU L Y, ZHANG W W, KOU J Q, et al. Machine learning methods for turbulence modeling in subsonic flows around airfoils[J]. Physics of Fluids, 2019, 31(1): 015105.DOI: 10.1063/1.5061693[LinkOut]
[19] SINGH A P, DURAISAMY K. Using field inversion to quantify functional errors in turbulence closures[J]. Physics of Fluids, 2016, 28(4): 045110.DOI: 10.1063/1.4947045[LinkOut]
[20] PARISH E J, DURAISAMY K. A paradigm for data-driven predictive modeling using field inversion and machine learning[J]. Journal of Computational Physics, 2016, 305: 758-774.DOI: 10.1016/j.jcp.2015.11.012[LinkOut]
[21] LING J L, KURZAWSKI A, TEMPLETON J. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance[J]. Journal of Fluid Mechanics, 2016, 807: 155-166. doi: 10.1017/jfm.2016.615[LinkOut]
[22] SCHMELZER M, DWIGHT R P, CINNELLA P. Discovery of algebraic Reynolds-stress models using sparse symbolic regression[J]. Flow, Turbulence and Combustion, 2020, 104(2-3): 579-603.DOI: 10.1007/s10494-019-00089-x[LinkOut]
[23] WANG J X, WU J L, XIAO H. Physics-informed machine learning approach for reconstructing Reynolds stress modeling discrepancies based on DNS data[J]. Physical Review Fluids, 2017, 2(3): 1-22.
[24] WU J L, XIAO H, PATERSON E. Physics-informed machine learning approach for augmenting turbulence models: A omprehensive framework[J]. Physical Review Fluids, 2018, 3(7): 074602.DOI: 10.1103/physrevfluids.3.074602[LinkOut]
[25] YIN Y H, YANG P, ZHANG Y F, et al. Feature selection and processing of turbulence modeling based on an artificial neural network[J]. Physics of Fluids, 2020, 32(10): 105117.DOI: 10.1063/5.0022561[LinkOut]
[26] LI H R, ZHANG Y F, CHEN H X. Aerodynamic prediction of iced airfoils based on modified three-equation turbulence model[J]. AIAA Journal, 2020, 58(9): 3863-3876.DOI: 10.2514/1.J059206[LinkOut]
[27] TRACEY B, DURAISAMY K, ALONSO J. Application of supervised learning to quantify uncertainties in turbulence and combustion modeling[C]// 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine (Dallas/Ft. Worth Region), Texas. Reston, Virginia: AIAA, 2013. doi: 10.2514/6.2013-259
[28] LING J L, JONES R, TEMPLETON J. Machine learning strategies for systems with invariance properties[J]. Journal of Computational Physics, 2016, 318: 22-35. doi: 10.1016/j.jcp.2016.05.003[LinkOut]
[29] POPE S B. A more general effective-viscosity hypothesis[J]. Journal of Fluid Mechanics, 1975, 72(2): 331-340.DOI: 10.1017/s0022112075003382[LinkOut]
[30] SPALART P R, DECK S, SHUR M L, et al. A new version of detached-eddy simulation, resistant to ambiguous grid densities[J]. Theoretical and Computational Fluid Dynamics, 2006, 20(3): 181-195.DOI: 10.1007/s00162-006-0015-0[LinkOut]
[31] RISTORCELLI J R. Diagnostic Statistics for the assessment and characterization of complex turbulent flows[R]. NASA-CR 198221, 1995.
[32] ADDY H, BROEREN A, ZOECKLER J, et al. A wind tunnel study of icing effects on a business jet airfoil[C]// 41st Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virginia: AIAA, 2003. doi: 10.2514/6.2003-727
[33] NASA. CFL3D Version 6 [EB/OL]. https://cfl3d.larc.nasa.gov
[34] PEDREGOSA F, VAROQUAUX G, GRAMFORT A, et al. Scikit-learn: Machine learning in Python[J]. Journal of Machine Learning Research, 2011, 12(1): 2825−2830.
-
期刊类型引用(6)
1. 张盟,王龙. 基于混合神经网络的风力机翼型流场预测. 人工智能. 2025(02): 50-56 .  百度学术
百度学术
2. 龙家俊,刘陈飘,秦飞,张加乐,徐圣冠,高宜胜. 基于Liutex的数据驱动湍流模型修正. 航空学报. 2024(15): 226-239 .  百度学术
百度学术
3. 杨茂桃,梁爽,易淼荣,田野,郭明明,乐嘉陵,张华. 基于深度神经网络的超声速隔离段湍流涡黏性系数辨识. 航空动力学报. 2023(02): 312-324 .  百度学术
百度学术
4. 刘宇豪,刘正先,李孝检. 基于PINN方法的不可压流场求解. 船舶工程. 2023(11): 150-155 .  百度学术
百度学术
5. 张浩男,王尊策,徐艳,张井龙,李森,闫月娟. 基于人工神经网络的空化射流气体体积分数预测及喷嘴结构优化. 化工机械. 2022(02): 248-255 .  百度学术
百度学术
6. 尧少波,何伟峰,陈丽华,吴昌聚,陈伟芳. 融合物理的神经网络方法在流场重建中的应用. 空气动力学学报. 2022(05): 30-38 .  本站查看
本站查看
其他类型引用(2)




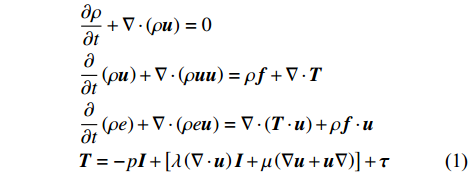
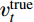
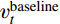
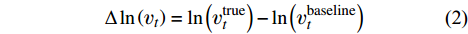
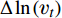

 下载:
下载: