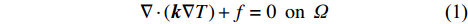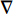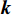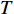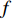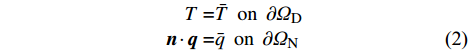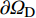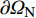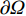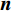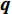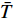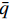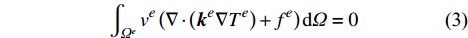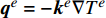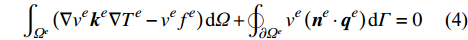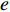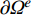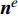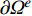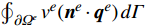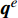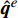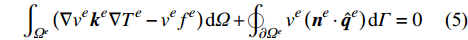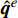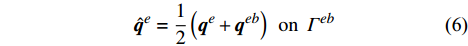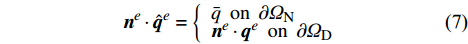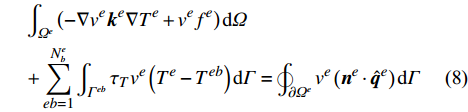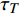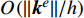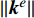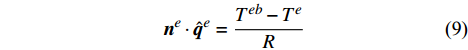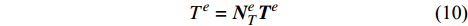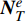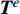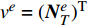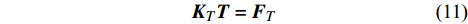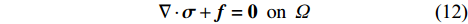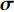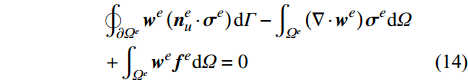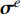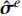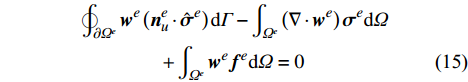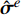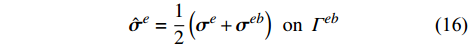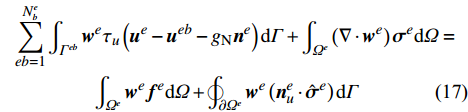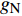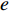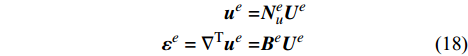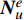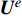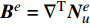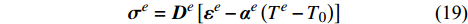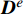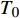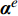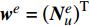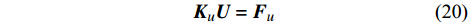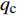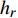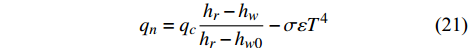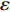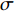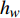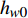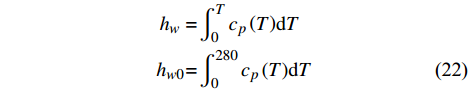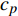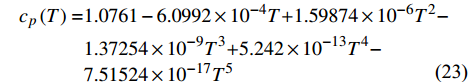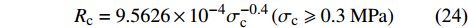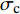A zonal coupled continuous/discontinuous Galerkin finite element method for vehicle structure analyses under aerodynamic force/heating effects
-
摘要: 高超声速飞行器热防护结构中存在大量不同材料的装配界面,因此在结构热力耦合分析中会产生界面非完好接触、热力耦合等非线性效应。针对传统三维有限元方法在求解此类结构时存在的计算量大、计算效率低的问题,建立了适用于含搭接界面温度场和热力耦合分析的分区连续/间断伽辽金有限元方法,充分考虑材料非线性以及温度和应力相关的接触热阻对结构热力耦合响应的影响,并编制相应的有限元计算软件,形成适应于工程大规模计算的含多材料搭接界面结构的三维传热、热力耦合问题研究的高效高精度计算能力,为我国新型高超声速飞行器热气动弹性特性预测及安全评估等提供研究手段和技术支撑。Abstract: Assembly interfaces between dissimilar materials widely exist in thermal protection structures of hypersonic aircrafts. The resulting imperfect contact and thermomechanical coupling need to be carefully considered in structural analyses. Since the traditional three-dimensional finite element method is computational expensive and inefficient, a new zonal coupled continuous/discontinuous Galerkin finite element method is established especially for the thermal and thermomechanical analyses of problems with dissimilar-material assembly interfaces. The effects of material nonlinearity, temperature, and stress-dependent thermal contact resistance to the structural thermomechanical coupling response are taken into account. In addition, an efficient and accurate finite element software suitable for large-scale engineering computations and three-dimensional thermal and thermomechanical coupling analyses of problems with dissimilar-material assembly interfaces is developed. This software provides a research tool and technical supports for the aerothermoelasticity prediction and safety evaluation of novel hypersonic aircrafts.
-
0. 引 言
近空间高超声速飞行器是当前国内外的研究热点之一,其发展水平也是一个国家综合国力的重要体现[1]。近空间高超声速飞行器的研发涉及到气动布局、气动加热环境模拟、结构热防护、发动机研制、航空航天材料、高能燃料、全球定位、矢量控制等多学科技术问题,其中热防护结构是起到决定性作用的一项关键技术[2-4]。对热防护结构的设计及安全评估涉及到气动热力耦合分析,即高超声速飞行引起的气动力和气动热对飞行器结构的传热防热及热力耦合行为的影响[5- 6],以及由此引起的热气弹问题[7- 8]。
国内外研究者针对气动热力耦合问题分析开展了大量的研究工作,取得了一系列丰富的研究成果。桂业伟等给出了气动力/热与结构热响应多场耦合问题的数据流程,深入探讨了多物理场耦合的策略与方法[9]。郭亮等建立了一种针对流场-热-结构的多场耦合分析方法,实现了对固体隔绝内外流场温度动态变化问题的仿真分析[10]。张章等利用流固及热固单向耦合的方法分析了考虑高超声速流场气动压力和气动热作用下空间再入充气结构的特性变化[11]。张胜涛等基于松耦合分析策略框架分析了高超声速流场-热-结构耦合问题,采用自适应耦合计算时间步长、混合插值策略和复杂外形网格变形等方法,实现了多场耦合分析平台[12]。Huang等建立了一体化热气弹耦合的计算框架,基于松耦合方法分析了复合材料双曲浅壳的温度场及热应力分布[13]。Li等基于有限体积法建立了高超声速飞行器圆柱形前缘的空气动力-结构-传热一体化分析方法[14]。Huang等建立了针对热防护系统的流-固-热紧耦合数值方法,与松耦合相比,紧耦合需要增加内部迭代过程。研究结果表明,紧耦合方法可以降低时滞效应并增加时间步长,但是由于迭代量的增加实际计算时间花费并未降低[15- 16]。Chen等基于松耦合方法建立了时间步长可自适应改变的高超声速飞行器前缘结构的气动-热-力耦合分析方法[17]。
特别的,为了提高结构热防护的效率,不同的飞行器结构部位采用的防热结构和使用的防热材料体系也往往不同,因此产生了大量的异种材料装配界面。装配界面会导致两方面的问题,一是非完好接触的装配界面会产生阻碍热量流动的接触热阻,从而对结构温度场产生影响,二是由于界面两侧不同材料的热物性参数可能相差很大,由此带来了严重的热失配问题。由于界面接触热阻受界面温度和界面接触应力的影响,因此形成了复杂的耦合关系,如图1所示。
对于含接触热阻的多场耦合问题,采用间断伽辽金有限元方法进行处理是一种很自然的选择[18-19]。间断伽辽金方法最早是为了求解中子输运的双曲型方程[20],间断伽辽金有限元法既能够像经典有限元方法一样处理复杂边界问题,又吸收了有限差分法的优点,适用于显式求解。间断伽辽金有限元方法允许单元的插值函数存在间断,可以采用不一致的网格划分以及利用间断的分片多项式构造近似函数和权函数空间,在构造高阶单元时具有很大的灵活性,可以较好地进行网格加密及升阶和并行化[21];间断伽辽金有限元方法不再强制单元之间必须协调连续,因此可以避免诸如薄膜自锁、剪切自锁、体积自锁等现象,且提高了解的计算精度和收敛性[22];数值通量的引入进一步消除了间断处的虚假数值振动,相当于计算流体力学中的人工黏性,因此在处理高梯度以及间断问题上很有优势[23];同时由于采用间断的插值函数,因此非常适合含间断问题的处理。但是间断伽辽金有限元方法的最大弱点在于计算量大,特别是对于三维问题[24]。因此,将间断伽辽金有限元方法和传统连续伽辽金方法结合起来就成为一种更好的选择[24]。Nguyen等研究了基于间断伽辽金有限元方法的气动热力耦合问题中界面的自适应处理方法[25]。刘冬欢等研究了接触热阻对疏导式热防护结构传热防热效果的影响[26]。关于气动热力多场耦合问题虽然已经有了大量的研究,但是针对考虑接触热阻的气动热力耦合问题,国内外相关的研究并不多见。
由于非完好接触界面的存在,产生了由界面接触热阻诱导的非线性热力耦合、由高温引起的材料热物性的非线性等复杂的非线性效应,传统的三维有限元计算方法在求解此类问题时遇到了严重的挑战,不仅计算规模大、计算效率低而且计算精度有限,给工程设计带来了极大的不便,成为制约我国新型高超声速飞行器结构设计及安全评估的瓶颈问题之一。在国家数值风洞工程项目的支持下,本文建立了分区耦合的间断/连续伽辽金有限元方法及其算法框架,并编制相应的有限元计算软件,形成适应于工程大规模计算的含多材料搭接界面结构的三维传热、热力耦合问题研究的计算分析能力,这对提高我国高超声速飞行器结构性能预测水平及优化设计等具有重要意义。
1. 有限元格式及计算流程
1.1 气动节点数据向有限元节点的转换方法
虽然国内外针对流固界面数据交互方法进行了大量的研究,但是很多往往过于理论化,采用非常复杂的插值方法来重构界面物理场。Pidaparti通过等参映射实现结构分析和流体分析界面的数据转换[27],三点挑方法将气动网格节点上的气动力按照静力等效原则分配到邻近的三个结构点上,三点挑方法可以推广到多点挑方法,本质上是要求离气动点近的结构点多分配一些载荷而远的少分配一些[28]。Liu等通过一个基于表面样条理论的转换矩阵将流场节点位移列向量用结构有限元节点位移列向量来表示,同时基于虚功原理将流场网格上的压力转换到结构网格上的有限元节点力[29]。刘深深等提出一种基于几何尺度进行归一化的高超声速飞行器多场耦合数据传递新方法[30]。张建刚等采用样条曲面拟合的方法得到翼面压力分布曲面,由该曲面得到有限元节点上的压力值,再在有限元模型单元上积分得到有限元节点载荷供强度设计使用[31]。这种数据插值拟合效果的好坏很大程度上取决于数据点的分布情况,若某个区域数据点分布较少,则很难通过插值的方法恢复该区域,因为这个区域已知的信息量不足以高精度地恢复数据。由于多场耦合分析涉及多次迭代计算,要求气动节点数据向有限元节点转换的效率一定要高,因此本文从工程实用的角度出发,开发流固界面数据转换软件。基本的思想是确定待定有限元节点在气动网格内的归属单元,即有限元节点被哪个气动单元所包围。这可以通过比较节点坐标范围的方法进行判断,接下来基于有限元节点在气动单元内部的不同位置,基于多点挑或插值的方法来确定有限元节点的场量值。
1.2 温度场分析的连续/间断有限元格式
考虑边界为
∂Ω 的区域Ω 上的椭圆型热传导方程:\nabla \cdot \left( {{\boldsymbol{k}}\nabla T} \right) + f = 0\;\;{\rm{ on }}\;\;\varOmega (1) 其中,
\nabla 为梯度算子,{\boldsymbol{k}} 是热传导系数矩阵,一般是对称的,T 为温度,f 是热源函数。问题的Dirichlet边界条件和Neumann边界条件分别为:\begin{split} T =& \bar T\;\;{\rm{ on }}\;\;\partial {\varOmega _{\rm{D}}} \\ {\boldsymbol{n}} \cdot {\boldsymbol{q}} =& \bar q\;\;{\rm{ on }}\;\;\partial {\varOmega _{\rm{N}}} \end{split} (2) 其中,
{\rm{ }}\partial {\varOmega _{\rm{D}}} 和\partial {\varOmega _{\rm{N}}} 分别表示Dirichlet边界和Neumann边界,边界\partial \varOmega 的单位外法线为{\boldsymbol{n}} ,热流密度为{\boldsymbol{q}} ,边界上给定的温度和热流密度分别为\bar T 和\bar q 。等效积分弱形式的热传导方程可写成:
\int_{{\varOmega ^e}} {{v^e}\left( {\nabla \cdot \left( {{{\boldsymbol{k}}^e}\nabla {T^e}} \right) + {f^e}} \right){\rm{d}}\varOmega } = 0 (3) 其中,热流密度为
{{\boldsymbol{q}}^{e}} = - {{\boldsymbol{k}}^{e}}\nabla {T^{e}} 。通过分部积分可以得到其等效形式:\begin{array}{l} \displaystyle\int_{{\varOmega ^e}} {\left( {\nabla {v^e}{{\boldsymbol{k}}^e}\nabla {T^e} - {v^e}{f^e}} \right){\rm{d}}\varOmega } + \displaystyle\oint_{\partial {\varOmega ^e}} {{v^e}\left( {{{\boldsymbol{n}}^e} \cdot {{\boldsymbol{q}}^e}} \right){\rm{d}}\varGamma } = 0 \end{array} (4) 其中,单元
{e} 的边界\partial {\varOmega ^e} 上的外法线为{{\boldsymbol{n}}^{e}} 。上式可见,单元边界
\partial {\varOmega ^{e}} 上的积分项\oint_{\partial {\varOmega ^{e}}} {{v^{e}}} {\left( {{{\boldsymbol{n}}^{e}} \cdot {{\boldsymbol{q}}^{e}}} \right){d}\varGamma } 出现在单元平衡方程中,在间断伽辽金有限元方法中单元内部边界上允许场变量出现间断,该积分项不能随意消去,可通过定义在单元边界上的Bassi-Rebay型数值通量来考虑这种间断效应,间断伽辽金有限元方法就是通过将单元边界热流{{\boldsymbol{q}}^{e}} 用其对应的热流数值通量{\hat {\boldsymbol{q}}^{e}} 进行替换来实现的,即单元的间断伽辽金有限元方程为:\begin{array}{l} \displaystyle\int_{{\varOmega ^e}} {\left( {\nabla {v^e}{{\boldsymbol{k}}^e}\nabla {T^e} - {v^e}{f^e}} \right){\rm{d}}\varOmega } + \displaystyle\oint_{\partial {\varOmega ^e}} {{v^e}\left( {{{\boldsymbol{n}}^e} \cdot {{\hat {\boldsymbol{q}}}^e}} \right){\rm{d}}\varGamma } = 0 \end{array} (5) 其中,热流数值通量
{\hat {\boldsymbol{q}}^e} 为:{\hat {\boldsymbol{q}}^e} = \frac{1}{2}\left( {{{\boldsymbol{q}}^e} + {{\boldsymbol{q}}^{eb}}} \right)\;\;{\rm{ on }}\;\;{\varGamma ^{eb}} (6) 这里,上标“eb”代表单元e的邻居单元。而在单元外边界上,数值通量取为:
{{\boldsymbol{n}}^e} \cdot {\hat {\boldsymbol{q}}^e} = \left\{ \begin{array}{l} \bar q\;\;{\rm{ on }}\;\;\partial {\varOmega _{\rm{N}}} \\ {{\boldsymbol{n}}^e} \cdot {{\boldsymbol{q}}^e}\;\;{\rm{ on }}\;\;\partial {\varOmega _{\rm{D}}} \\ \end{array} \right. (7) 同时必须在边界上加入稳定项,这里将单元内部边界基本场变量的跳变引入到平衡方程中,称为稳定项,此时单元间断伽辽金有限元方程可写成:
\begin{split}& \int_{{\varOmega ^e}} {\left( { - \nabla {v^e}{{\boldsymbol{k}}^e}\nabla {T^e} + {v^e}{f^e}} \right){\rm{d}}\varOmega }\\& + \sum\limits_{eb = 1}^{N_b^e} {\int_{{\varGamma ^{eb}}} {{\tau _T}{v^e}\left( {{T^e} - {T^{eb}}} \right){\rm{d}}\varGamma } } = \oint_{\partial {\varOmega ^e}} {{v^e}\left( {{{\boldsymbol{n}}^e} \cdot {{\hat {\boldsymbol{q}}}^e}} \right){\rm{d}}\varGamma } \end{split} (8) 其中,温度稳定化参数
{\tau _T} 是O\left( {{{\left\| {{{\boldsymbol{k}}^e}} \right\|} / h}} \right) 量级的正数,这里\left\| {{{\boldsymbol{k}}^e}} \right\| 是热传导系数矩阵的某种范数,h是单元的特征尺寸。在引入界面的非完全热接触条件时,首先需要将单元间断伽辽金有限元方程中的温度稳定化参数赋零,同时将界面的热流数值通量由非完全接触的定量描述即接触热阻的定义式给出:
{{\boldsymbol{n}}^e} \cdot {\hat {\boldsymbol{q}}^e} = \frac{{{T^{eb}} - {T^e}}}{R} (9) 同时为了体现这种强的间断效应,在存在接触热阻的单元内边界上要将稳定化参数赋零。
假设单元温度场可以表示为:
{T^e} = {\boldsymbol{N}}_T^e{{\boldsymbol{T}}^e} (10) 这里,
{\boldsymbol{N}}_T^e 为温度场插值函数,{{\boldsymbol{T}}^e} 为单元节点的温度列向量。权函数取为{v^e} = {( {{\boldsymbol{N}}_T^e} )^{\rm{T}}} ,代入单元有限元方程,并引入气动热载荷和辐射边界条件,经过推导并组装可得用温度节点列向量为唯一未知量的结构总体传热有限元方程组:{{\boldsymbol{K}}_T}{\boldsymbol{T}} = {{\boldsymbol{F}}_T} (11) 在引入强制温度边界条件并求解此方程组即可得到结构的温度场,如果考虑材料属性的温度相关性或者接触热阻的温度相关性,则需要进行迭代求解,进一步可得到热流密度场等相关场量。这样就自然地将接触热阻引入到单元平衡方程中来,避免了采用界面单元的麻烦。而在不存在接触热阻的地方,可以采用经典的连续伽辽金有限元方法,无需稳定项和数值通量项,从而大大提高了计算效率。
1.3 位移场分析的连续/间断有限元格式
结构位移场分析的平衡方程可写成:
\nabla \cdot {\boldsymbol{\sigma}} + {\boldsymbol{f}} = {\bf{0}}\;\;{\rm{ on }}\;\;\varOmega (12) 其中,
{\boldsymbol{\sigma }} 为应力向量,{\boldsymbol{f}} 为体力向量,\nabla 为微分算子。平衡方程的等效积分弱形式可写成:
\int_{{\varOmega ^e}} {{{\boldsymbol{w}}^e}\left( {\nabla \cdot {{\boldsymbol{\sigma}} ^e} + {{\boldsymbol{f}}^e}} \right){\rm{d}}\varOmega } = 0 (13) 其中,
{{\boldsymbol{w}}^e} 为定义在区域\varOmega 上矢量形式的权函数。通过分部积分可以得到其等效形式:
\begin{split}& \oint_{\partial {\varOmega ^e}} {{{\boldsymbol{w}}^e}\left( {{\boldsymbol{n}}_u^e \cdot {{\boldsymbol{\sigma}} ^e}} \right){\rm{d}}\varGamma } - \int_{{\varOmega ^e}} {\left( {\nabla \cdot {{\boldsymbol{w}}^e}} \right){{\boldsymbol{\sigma}} ^e}{\rm{d}}} \varOmega \\ \qquad\qquad&+ \int_{{\varOmega ^e}} {{{\boldsymbol{w}}^e}{{\boldsymbol{f}}^e}{\rm{d}}\varOmega } = 0 \end{split} (14) 通过将单元边界应力
{{\boldsymbol{\sigma}} ^e} 用应力数值通量{\hat {\boldsymbol{\sigma}} ^e} 进行替换即可得到单元应力分析的间断伽辽金有限元方程:\begin{split}& \oint_{\partial {\varOmega ^e}} {{{\boldsymbol{w}}^e}\left( {{\boldsymbol{n}}_u^e \cdot {{\hat {\boldsymbol{\sigma}} }^e}} \right){\rm{d}}\varGamma } - \int_{{\varOmega ^e}} {\left( {\nabla \cdot {{\boldsymbol{w}}^e}} \right){{\boldsymbol{\sigma}} ^e}{\rm{d}}} \varOmega \\& \qquad\qquad+\int_{{\varOmega ^e}} {{{\boldsymbol{w}}^e}{{\boldsymbol{f}}^e}{\rm{d}}\varOmega } = 0 \end{split} (15) 这里,Bassi-Rebay型应力数值通量
{\hat {\boldsymbol{\sigma}} ^e} 定义为:{\hat {\boldsymbol{\sigma}} ^e} = \frac{1}{2}\left( {{{\boldsymbol{\sigma}} ^e} + {{\boldsymbol{\sigma}} ^{eb}}} \right)\;\;{\rm{ on }}\;\;{\varGamma ^{eb}} (16) 和温度场分析时引入接触界面条件类似,应力场分析时需要引入位移的不可穿透条件。不可穿透条件意味着接触界面两侧的节点不能互相穿透对方的表面而进入其内部,这在数值计算中是一个很难处理的不等式约束问题。一般有两种方法可用于引入不可穿透条件,一种是采用界面单元来耦合接触区域,通过给定界面单元的刚度与节点相对位置之间的关系来描述各种各样的接触状态;另一种是在计算格式中直接施加位移约束,这需要首先进行接触搜索确定接触对,进而采用诸如罚函数方法、拉格朗日乘子法、约束函数方法等对接触对施加位移约束。与此同时,在许多工程实际问题中罚函数方法已经被证明是很高效的。另一方面,这也同间断伽辽金有限元方法实现无接触单元界面位移连续的稳定项是一致的,因此这里我们采用罚函数方法来引入接触界面的不可穿透条件。此时有:
\begin{split}& \sum\limits_{eb = 1}^{N_b^e} {\int_{{\varGamma ^{eb}}} {{{\boldsymbol{w}}^e}{\tau _u}\left( {{{\boldsymbol{u}}^e} - {{\boldsymbol{u}}^{eb}} - {g_{\rm{N}}}{{\boldsymbol{n}}^e}} \right){\rm{d}}\varGamma } } + \int_{{\varOmega ^e}} {\left( {\nabla \cdot {{\boldsymbol{w}}^e}} \right){{\boldsymbol{\sigma}} ^e}{\rm{d}}} \varOmega= \\& \qquad\qquad \int_{{\varOmega ^e}} {{{\boldsymbol{w}}^e}{{\boldsymbol{f}}^e}{\rm{d}}\varOmega } + \oint_{\partial {\varOmega ^e}} {{{\boldsymbol{w}}^e}\left( {{\boldsymbol{n}}_u^e \cdot {{\hat {\boldsymbol{\sigma}} }^e}} \right){\rm{d}}\varGamma } \\[-14pt] \end{split} (17) 其中,
{g_{\rm{N}}} 表示单元e与其邻居单元eb之间的初始预留间隙。假设单元
e 的位移场和应变场通过插值可以表示为:\begin{split} {{\boldsymbol{u}}^e} =& {\boldsymbol{N}}_u^e{{\boldsymbol{U}}^e} \\ {{\boldsymbol{\varepsilon}} ^e} = {\nabla ^{\rm{T}}}{{\boldsymbol{u}}^e} =& {{\boldsymbol{B}}^e}{{\boldsymbol{U}}^e} \end{split} (18) 其中,
{\boldsymbol{N}}_u^e 为单元位移场的插值函数矩阵,{{\boldsymbol{U}}^e} 为单元节点位移列向量,{{\boldsymbol{B}}^e} = {\nabla ^{\rm{T}}}{\boldsymbol{N}}_u^e 为几何矩阵。进行应力场分析时,需要考虑温度产生的变形,此时的本构方程为:
{{\boldsymbol{\sigma}} ^e} = {{\boldsymbol{D}}^e}\left[ {{{\boldsymbol{\varepsilon}} ^e} - {{\text{α}} ^e}\left( {{T^e} - {T_0}} \right)} \right] (19) 其中,
{{\boldsymbol{D}}^e} 是弹性矩阵,{T_0} 是计算热变形的参考温度,{{{ {\text{α}}}} ^{e}} 是材料的热膨胀系数向量。取权函数为
{{\boldsymbol{w}}^e} = {\left( {{\boldsymbol{N}}_u^e} \right)^{\rm{T}}} ,代入单元有限元方程,并引入气动力热载荷,经过推导并组装可得到用位移节点列向量为唯一未知量的结构总体有限元方程组:{{\boldsymbol{K}}_u}{\boldsymbol{U}} = {{\boldsymbol{F}}_u} (20) 引入强制位移边界条件即可求解整体有限元方程组,得到结构位移场,进一步经过应力磨平等处理即可得到高精度的应力场。
值得注意的是,本文假设结构的变形处于小变形状态,因此热应力对结构的影响仅体现在等效载荷列向量中,并未考虑其对结构几何刚度的影响。
1.4 计算流程及软件开发
求解多场耦合问题的基本方法有紧耦合和松耦合两种,本文采用松耦合的方法通过迭代得到耦合问题的解,具体的计算流程图如图2所示。
首先进行流固界面载荷转换,输入气动热力计算结果和结构有限元网格信息,利用界面载荷转换程序得到有限元节点或者单元上的气动热流和气动力信息。
其次输入必须的各种数据,包括几何信息,比如有限元网格的单元组成和节点坐标;材料属性信息,比如随温度变化的热学参数(热导率、热膨胀系数),力学参数(弹性模量、泊松比、塑性参数),接触热阻模型;载荷信息(经过界面场量转换软件得到的有限元节点上的气动力和气动热流密度、结构位移约束类型及所在的位置);控制参数(比如分析类型、收敛准则、自适应策略、初始化参数等)。
基于初始化的参数进行温度场的试算,并判断当前温度场是否收敛:如不收敛,则对温度场插值单元进行升阶或者加密网格并重新计算;如收敛,则继续进行位移场和应力场的计算。得到位移场和应力场结果之后,需要对位移场结果进行收敛性判断:如不收敛,则进行单元插值函数升阶或网格加密再计算;如收敛,那么基于当前的界面接触应力场和接触热阻模型,对界面接触热阻进行更新,并与之前的界面接触热阻进行收敛性判断:如不收敛,则需要基于当前的新界面接触热阻重新回到温度场计算;如收敛,则针对计算得到的结果进行后处理并输出结果,计算结束。
基于上述有限元格式和计算流程图编制了相应的计算程序,开发了相配套的软件,并作为一个功能模块集成到国家数值风洞软件群中。
2. 算法验证
2.1 问题描述
为验证算法的准确性,构建了如图3所示由四面体单元构成的组合杆件,将本文结果同有限元软件仿真结果对比分析。杆件1长度为0.4 m,材料热导率为30 W/m·K,热膨胀系数为10×10−6 /K,弹性模量为200 GPa;杆件2长度为0.2 m,材料热导率为100 W/m·K,热膨胀系数为15×10−6/K,弹性模量为200 GPa。泊松比均为0.3。组合杆件左右两端分别给定恒温300 K和700 K,界面热阻为1×10−3 m2·K/W。左右两端位移固定,热变形参考温度300 K。
2.2 结果对比
图4~图6分别给出了组合杆件温度场、总位移场(USUM)和等效应力场(SEQV)基于本文有限元程序结果和通用有限元软件结果的对比。同时选取了组合杆件轴线方向截面中心处的一条路径,通过场量沿该路径的分布图比较不同界面接触热阻R下两种方法的计算结果误差,见图7,并在组合杆件中心选择同一位置比较等效应力的结果误差,见表1。
从以上结果对比可以看出,接触热阻的存在导致温度场分布在界面处产生跳变,接触热阻越大,温度的跳变越大。沿轴线路径上的温度场和位移场以及杆件中点处的等效应力数值,本文程序结果和理论解及通用软件结果一致,杆件中点处的等效应力的相对误差不超过0.4%。除此算例外,本文有限元程序在设计开发中,基于软件工程的思想,对所有的边界材料、材料属性、结构形式、载荷形式进行了全方位的测试,本程序结果均与通用有限元软件结果或者理论解完全吻合,这充分说明了本文程序的精度和可靠性,可进一步用于实际工程结构的数值仿真。
表 1 组合杆件中点位置的等效应力Table 1. Equivalent stress at the center of the composite rodThermal contact resistance/ (m2·K·W–1) 5×10–3 1×10–3 1×10–4 Equivalent stress/MPa (v = 0.3) ANSYS 582.7 625.0 631.7 Present 580.2 622.7 632.8 Equivalent stress/MPa (v = 0) Analytical 554.4 592.8 604.4 Present 553.2 594.4 605.5 3. 工程算例
3.1 问题描述
图8为高速飞行器的水平舵面模型图,整体结构由翼前缘和翼后舵结构(蒙皮、蜂窝夹心、结构骨架组成)构成,材料均为GH99。翼根处弦长约537 mm,翼梢处弦长约380 mm,翼展约317 mm,翼面由三个折面组成。针对飞行器强烈的气动加热现象,首先基于给定的冷壁热流和恢复焓对水平舵结构进行热分析,进而同时考虑气动力和气动加热的作用,对结构的热强度进行计算分析。温度场分析时需考虑翼前缘与翼后舵之间的界面接触热阻的影响。
3.2 流固界面气动热力转换
基于1.1节的转换方法得到的转换结果如图9~图11所示。结构温度场和应力场分析时需要给定气动热流、气动力边界条件,相关边界条件由CFD计算给出,提供的环境数据为翼面上各个气动节点的气动力、冷壁热流和恢复焓。由于气动网格节点和有限元分析网格的节点是不重合的,因此首先需要将CFD气动点的气动力、冷壁热流以及恢复焓转换到有限元分析时的单元结构节点上。
可以看出,飞行器飞行过程中,水平舵翼前缘承受较大的气动热和气动压强,基本在2 000 kW/m2和170 kPa左右,而舵面数值偏小,与前缘相差约为一个数量级。
由于本算例主要针对面分布的热流和气动压强进行转换,从快速确定有限元节点场量的角度出发,采用简化的转换算法,将距离有限元节点最近的气动点的场量值作为该有限元节点的场量值。
从转换前后气动和有限元的场量云图可以看出,在大部分区域的转换效果都很好,而在翼前缘区域由于转换前后网格差异较大,导致转换误差稍微大一些,同时由于该区域范围较小,因此转换误差对结构变形和应力的影响是可以忽略的。
3.3 边界条件以及热阻模型
进行热分析时对翼舵外表面施加给定热流边界条件,根据CFD计算得到的冷壁热流
{q_{\rm{c}}} 和恢复焓{h_r} 计算得到施加在结构上的热壁热流{q_n} 为:{q_n} = {q_c}\frac{{{h_r} - {h_w}}}{{{h_r} - {h_{w0}}}} - \sigma \varepsilon {T^4} (21) 这里考虑了舵面辐射散热效果,
\varepsilon 为Stefan-Boltzmann常数,取为5.67×10−8 W/m2K4,\sigma 为辐射系数,取为0.8,T为待求的壁面温度。焓值计算时的参考温度为280 K,壁面温度和参考温度条件下的焓值{h_w} 和{h_{w0}} 分别为:\begin{split} {h_w} =& \int_0^T {{c_p}\left( T \right)} {\rm{d}}T \\ {h_{w0}}{\rm{ = }}&\int_0^{280} {{c_p}\left( T \right)} {\rm{d}}T \end{split} (22) 其中,
{c_p} 为空气的定压比热容,在250~2500 K之间可通过数据拟合为:\begin{split} {c_p}\left( T \right)=&{\rm{ 1}}{\rm{.0761}} - {\rm{6}}{\rm{.0992}} \times {\rm{1}}{{\rm{0}}^{{\rm{ - 4}}}}T{\rm{ + 1}}{\rm{.59874}} \times {\rm{1}}{{\rm{0}}^{{\rm{ - 6}}}}{T^{\rm{2}}} -\\& {\rm{1}}{\rm{.37254}} \times {\rm{1}}{{\rm{0}}^{{\rm{ - 9}}}}{T^{\rm{3}}}{\rm{ + 5}}{\rm{.242}} \times {\rm{1}}{{\rm{0}}^{{\rm{ - 13}}}}{T^{\rm{4}}} -\\& {\rm{7}}{\rm{.51524}} \times {\rm{1}}{{\rm{0}}^{{\rm{ - 17}}}}{T^{\rm{5}}}\\[-10pt] \end{split} (23) 温度场分析时翼舵底部安装面给定温度280 K,辐射环境参考温度280 K,由于给定的热流边界条件与待求温度T相关,因此这是一个非线性温度场问题,依据上述程序进行迭代求解。
在对翼舵强度分析时,外表面施加给定的气动力载荷,翼舵安装面位移固定,热变形参考温度280 K,而界面接触热阻与界面应力密切相关[32-33]:
{R_{\rm{c}}} = 9.5626 \times {10^{ - 4}}\sigma _{\rm{c}}^{ - 0.4} \left( {{\sigma _{\rm{c}}} \geqslant 0.3\;{\rm{ MPa}}} \right) (24) 其中,
{\sigma _{\rm{c}}} 为界面接触应力,MPa。当应力较小时,界面接触热阻较大,随界面应力的增大,界面接触热阻随应力指数型减小。3.4 计算结果
3.4.1 结构温度场
基于上述有限元方法,在不考虑界面接触热阻时得到的结构温度场如图12所示。
从以上计算结果可以看出,由于水平舵两面气动热边界条件的差异导致了温度场分布的不同,其中前缘最高温度达到1276 K,舵面整体温度大致在600~1100 K之间。实际工程应用中,温度过高对结构变形影响较为显著,因此针对升温引起的结构应力变化的研究很有必要。
不同接触热阻时舵面温度场如图13所示,翼舵结构界面两侧节点温度随接触热阻的变化趋势如图14所示。
界面接触热阻在组合结构热传导过程中起到阻碍热量传递的作用,会造成界面两侧温度的跳变,从本翼舵算例结果可以看出,界面接触热阻越大界面两侧温度跳变越明显,但对于整体温度场分布的影响不明显,这是因为本算例中热流边界条件与辐射边界同时施加在翼舵外表面上,气动热和辐射相互作用的影响对于翼舵表面温度场的分布占据主导作用,因此界面接触热阻效果对于翼舵界面处热传导影响效果甚微,而对于非气动热外表面的接触界面,界面接触热阻会占据主导作用,极大地影响结构温度场和热防护效果。
3.4.2 结构位移场和应力场
在同时考虑气动压力、气动热以及界面接触热阻的情况下,利用前述有限元方法对翼舵结构进行热强度计算,得到的总体位移场和等效应力场如图15、图16所示。
从计算结果可以看出,如果同时考虑气动力与气动热的作用,由于GH99热膨胀系数较大,结构位移的变化主要由受热变形的主导,气动力对结构应力的变化影响较小。在翼舵与底盘装配区域等效应力是最大的,最大值可以达到600 MPa,在界面处,由于涉及到不同结构的装配,因此接触应力相对较高,接触热阻较小,因此界面对结构温度场的影响较小,界面接触热阻可忽略不计,无明显温度跳跃现象,界面两侧的应力场分布连续,整体结构仍处于材料的强度极限范围内。一般来讲,结构温度场对结构应力的分布影响较大,计算结果也表明了弹塑性变形对结构强度分析的重要性。因此,通过调控界面接触热阻去实现结构温度场的重分布,从而影响结构的等效应力场,是一种提高结构安全性的有效手段。本算例充分展示了本文发展的分区耦合连续/间断伽辽金有限元方法和及编制的计算软件在处理气动-热-力耦合分析问题上的可行性。
4. 结 论
在国家数值风洞工程项目的支持下,采用松耦合的方法建立了气动热力耦合问题的连续/间断伽辽金有限元计算格式,充分考虑搭接结构在界面处广泛存在的非完好接触现象,引入温度和应力相关的界面接触热阻,在界面处使用间断伽辽金有限元方法,在连续区域采用经典的连续伽辽金有限元方法,极大提高了计算精度和计算效率,并编制了具有自主知识产权的气动-热-力耦合计算分析软件。数值算例验证了本文建立的方法和编制的计算软件的精度和可靠性,形成了大规模工程热力耦合问题的计算分析能力,为我国新型飞行器热防护结构的研发提供重要的技术支撑。下一步将建立瞬态温度场和结构动力学的连续/间断伽辽金有限元方法,将计算能力从静态扩展到动态分析,实现飞行全过程的实时高精度数值仿真。
-
表 1 组合杆件中点位置的等效应力
Table 1 Equivalent stress at the center of the composite rod
Thermal contact resistance/ (m2·K·W–1) 5×10–3 1×10–3 1×10–4 Equivalent stress/MPa (v = 0.3) ANSYS 582.7 625.0 631.7 Present 580.2 622.7 632.8 Equivalent stress/MPa (v = 0) Analytical 554.4 592.8 604.4 Present 553.2 594.4 605.5 -
[1] 尹志忠, 李强. 近空间飞行器及其军事应用分析[J]. 装备指挥技术学院学报. 2006;17(5): 64-68. doi: 10.3783/j.issn.1673-0127.2006.05.016 YIN Z Z, LI Q. Analysis of near space vehicle and its military application[J]. Journal of the Academy of Equipment Command & Technolog, 2006;17(5): 64-68.(in Chinese) DOI: 10.3783/j.issn.1673-0127.2006.05.016
[2] 杨亚政, 李松年, 杨嘉陵. 高超声速飞行器及其关键技术简论[J]. 力学进展. 2007;37(4): 537-550. doi: 10.3321/j.issn:1000-0992.2007.04.004 YAND Y Z, LI S N, YANG J L. A review on hypersonic vehicles and key technologies[J]. Advances in mechanics, 2007; 37(4): 537-550.(in Chinese) DOI: 10.3321/j.issn: 1000-0992.2007.04.004
[3] 桂业伟, 刘磊, 魏东. 长航时高超声速飞行器的综合热效应问题[J]. 空气动力学学报. 2020;38(4): 641-650. doi: 10.7638/kqdlxxb-2020.0078 Gui Y W, LIU L, WEI D. Combined thermal phenomena issues of long endurance hypersonic vehicles[J]. Acta Aerodynamica Sinica, 2020;38(4): 641-650.(in Chinese) DOI: 10.7638/kqdlxxb-2020.0078
[4] 桂业伟. 高超声速飞行器综合热效应问题[J]. 中国科学: 物理学力学天文学. 2019;49(11): 139-153. doi: 10.1360/SSPMA2019-0060 Gui Y W. Combined thermal phenomena of hypersonic vehicle[J]. SCIENTIA SINICA: Physica, Mechanica & Astronomica, 2019;49(11): 139-153.(in Chinese) DOI:CNKI:SUN:JGXK.0.2019-11-012
[5] 刘冬欢, 郑小平, 王飞, 等. 内置高温热管热防护结构传热防热机理研究[J]. 清华学报. 2010;50(7): 1094-1098. doi: 10.16511/j.cnki.qhdxxb.2010.07.020 LIU D H, ZHENG X P, WANG F, et al. Heat conduction and thermal protection mechanism of heat pipe cooled thermal protection structures[J]. Journal of Tsinghua University (Science and Technology), 2010;50(7): 1094-1098.(in Chinese) DOI: 10.16511/j.cnki.qhdxxb.2010.07.020
[6] 刘冬欢, 郑小平, 王飞, 等. 内置高温热管C/C复合材料热防护结构热力耦合机制[J]. 复合材料学报. 2010;27(3): 43-49. doi: 10.13801/j.cnki.fhclxb.2010.03.012 LIU D H, ZHENG X P, WANG F, et al. Mechanism of thermomechanical coupling of high temperature heat pipe cooled C/Ccomposite material thermal protection structure[J]. Acta Materiae Compositae Sinica, 2010;27(3): 43-49.(in Chinese) DOI: 10.13801/j.cnki.fhclxb.2010.03.012
[7] 刘磊, 桂业伟, 耿湘人, 等. 高超声速飞行器热气弹静态问题研究[J]. 空气动力学学报. 2013;31(5): 559-563. doi: 10.7638/kqdlxxb-2012.0006 LIU L, GUI Y W, GENG X R, et al. Study on static aerothermoelasticity for hypersonic vehicles[J]. Acta Aerodynamica Sinica, 2013;31(5): 559-563.(in Chinese) DOI: 10.7638/kqdlxxb-2012.0006
[8] 刘磊, 桂业伟, 耿湘人, 等. 热气动弹性变形对飞行器结构温度场的影响研究[J]. 空气动力学学报. 2015;33(1): 31-35. doi: 10.7638/kqdlxxb-2014.0119 LIU L, GUI Y W, GENG X R, et al. Study on the temperature field of hypersonic vehicle structure with aerothermoelasticity deformation[J]. Acta Aerodynamica Sinica, 2015;33(1): 31-35.(in Chinese) DOI: 10.7638/kqdlxxb-2014.0119
[9] 桂业伟, 刘磊, 耿湘人, 等. 气动力/热与结构多场耦合计算策略与方法研究[J]. 工程热物理学报, 2015(05): 1047-1051. GUI Y W, LIU L, GENG X R, et al. Study on the computation strategy and method of Areo-dynamic-thermal-structural coupling problem[J]. Mianyang: Journal of Engineering Thermophysics, 2015(05): 1047-1051.(in Chinese) DOI: CNKI:SUN:GCRB.0.2015-05-026
[10] 郭亮, 王一丁, 黄立, 等. 结构隔绝内-外空间的流-热-固耦合仿真应用[J]. 空气动力学学报, 2015, 33(2): 272-277. doi: 10.7638/kqdlxxb-2014.0134 GUO L, WANG Y D, HUANG L, et al. Fluid-thermal-structural coupled method for flow and temperature distribution of inner-outer flow filed isolated by structure[J]. Acta Aerodynamica Sinica, 2015;33(2): 272-277.(in Chinese) DOI: 10.7638/kqdlxxb-2014.0134
[11] 张章, 吴杰, 侯安平, 等. 空间再入充气结构的流固及热固单向耦合研究[J]. 空气动力学学报, 2018(6): 1061-1070. doi: 10.7638/kqdlxxb-2018.0033 ZHANG Z, WU J, HOU B P, et al. One way fluid-structure and thermo-structure interaction on an inflatable space re-entry aeroshell[J]. Acta Aerodynamica Sinica, 2018;36(6): 1061-1070.(in Chinese) DOI: 10.7638/kqdlxxb-2018.0033
[12] 张胜涛, 陈方, 刘洪. 高超声速进气道前缘流场-热-结构耦合分析[J]. 空气动力学学报. 2017;35(3): 436-443. doi: 10.7638/kqdlxxb-2017.0036 ZHANG S T, CHENG F, LIU H. Fluid-thermal-structural coupling analysis on leading edge of hypersonic inlets[J]. Acta Aerodynamica Sinica, 2017;35(3): 436-443.(in Chinese) DOI: 10.7638/kqdlxxb-2017.0036
[13] Huang D, Rokita T, Friedmann P P. Integrated aerothermoelastic analysis framework with application to skin panels[J]. AIAA Journal. 2018;56(11): 4562-4581. DOI: 10.2514/1.J056677
[14] Li J, Wang J. An integrated algorithm for hypersonic Fluid-thermal-structural analysis of aerodynamically heated cylindrical leading edge[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering. 2019;233(14): 5177-5191. DOI: 10.1177/0954410019841161
[15] Huang J, Yao W X, Shan X Y, et al. Coupled fluid-structural thermal numerical methods for thermal protection system[J]. AIAA Journal. 2019;57(8): 3630-3638. DOI: 10.2514/1.J057616
[16] Huang J, Yao W X, Shan X Y. Coupled fluid-thermal analysis of combinational nonablative thermal protection system concept[J]. Journal of Spacecraft and Rockets. 2019;56(4): 1137-1151. DOI: 10.2514/1.A34212
[17] Chen F, Liu H, Zhang S. Coupled heat transfer and thermo-mechanical behavior of hypersonic cylindrical leading edges[J]. International Journal of Heat and Mass Transfer. 2018;122: 846-862. DOI: 10.1016/j.ijheatmasstransfer.2018.02.037
[18] Liu D H, Zheng X P, Liu Y H. A discontinuous Galerkin finite element method for heat conduction problems with local high gradient and thermal contact resistance[J]. CMES - Computer Modeling in Engineering and Sciences. 2009;39(3): 263-299. DOI: 10.3970/cmes.2009.039.263
[19] Zheng X P, Liu D H, Liu Y H. Thermoelastic coupling problems caused by thermal contact resistance: A discontinuous Galerkin finite element approach[J]. Science China Physics Mechanics & Astronomy, 2011, 54(4): 666-674. DOI: 10.1007/s11433-011-4282-4
[20] REED W H, HILL T R. Triangular mesh methods for the neutron transport equation[R]. Los Alamos Report LA, 1973.
[21] COCKBURN B. Discontinuous Galerkin methods[M]. ZAMM Zeitschrift für Angewandte Mathematik und Mechanik. 2003, 83(11): 731-754.
[22] Eyck A T, Lew A. Discontinuous Galerkin methods for non-linear elasticity[J]. International Journal for Numerical Methods in Engineering. 2006, 67(9): 1204-1243. DOI: 10.1002/nme.1667
[23] 李锡夔, 姚冬梅. 弹塑性体中波传播问题的间断Galerkin有限元法[J]. 固体力学学报. 2003;24(4): 399-409. doi: 10.3969/j.issn.0254-7805.2003.04.004 LI X K, YAO D M. Discontinuous Galerkin finite element method for wave propagation problems in elasto-plastic continua[J]. Acta Mechanica Solida Sinica, 2003;24(4): 399-409.(in Chinese) DOI: 10.3969/j.issn.0254-7805.2003.04.004
[24] Engel G, Garikipati K, Hughes T, et al. Continuous/ discontinuous finite element approximations of fourth-order elliptic problems in structural and continuum mechanics with applications to thin beams and plates, and strain gradient elasticity[J]. Computer Methods in Applied Mechanics and Engineering, 2002, 191(34): 3669-3750. https://doi.org/10.1016/S0045-7825(02)00286-4
[25] Nguyen M, Errera M, O Labbé, et al. Adaptive interface treatment for aerothermal coupling using a discontinuous Galerkin method[J]. International Journal of Thermal Sciences, 2020, 149: 106208. DOI: 10.1016/j.ijthermalsci.2019.106208
[26] 刘冬欢, 尚新春. 接触热阻对疏导式热防护结构防热效果的影响. 航空学报. 2012;33(10): 1834-1841. ZHUANG F G, CUI E J, ZHANG H X, et al. Effect of thermal contact resistance on the performance of heat-pipe-cooled thermal protection structures[J]. Acta Aeronqutica et Astonautica Sinica, 2012;33(10): 1834-1841.(in Chinese)
[27] Pidaparti R M V. Structural and aerodynamic data transformation using inverse isoparametric mapping[J]. Journal of Aircraft. 1992;29(3): 507-509. DOI: 10.2514/3.46190
[28] 徐敏, 史忠军, 陈士橹. 一种流体-结构耦合计算问题的网格数据交换方法. 西北工业大学学报[J]. 2003;21(5): 532-535. doi: 10.3969/j.issn.1000-2758.2003.05.006 Xu Min, Shi Z J, Chen S L. A suitable method for transferring information between CFD and CSD grids[J]. Journal of Northwestern Polytechnical University. 2003;21(5): 532-535.(in Chinese) DOI: 10.3969/j.issn.1000-2758.2003.05.006
[29] Liu F, Cai J, Zhu Y, et al. Calculation of wing flutter by a coupled fluid-structure method[J]. Journal of Aircraft. 2001;38(2): 334-340. DOI: 10.2514/2.2766
[30] 刘深深, 桂业伟, 唐伟, 等. 一种多场耦合数据传递新方法[J]. 宇航学报. 2016;37(1): 61-67. doi: 10.3873/j.issn.1000-1328.2016.01.008 Liu S S, Gui Y W, Tang W, et al. A new data transfer method in fluid-thermal-structure coupling problems[J]. Journal of Astronautics. 2016;37(1): 61-67.(in Chinese) DOI: 10.3873/j.issn.1000-1328.2016.01.008
[31] 张建刚, 孙仁俊, 唐长红. 大型飞机气动载荷向有限元节点等效分配的方法[J]. 力学与实践. 2017;39(1): 25-29. doi: 10.6052/1000-0879-16-170 Zhang J G, Sun R J, Tang C H. The method of transferring aerodynamic load to FEM nodes for large airplane[J]. Mechanics in Engineering, 2017, 39(1): 25-29(in Chinese) DOI: 10.6052/1000-0879-16-170
[32] Tauchert T R, Leigh D C, Tracy M A. Measurements of thermal contact resistance for steel layered vessels[J]. Journal of Pressure Vessel Technology, 1988, 110(3): 335. DOI: 10.1115/1.3265608
[33] Barber J, Zhang R. Transient behaviour and stability for the thermoelastic contact of two rods of dissimilar materials[J], International Journal of Mechanical Sciences, 1988, 30(9): 691-704. DOI: 10.1016/0020-7403(88)90096-3
-
期刊类型引用(1)
1. 徐世南,徐立友. 空空导弹热力环境耦合分析. 国防科技大学学报. 2025(02): 109-119 .  百度学术
百度学术
其他类型引用(2)





 下载:
下载: