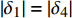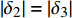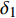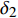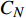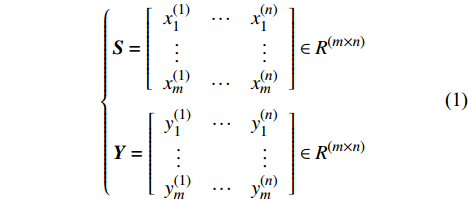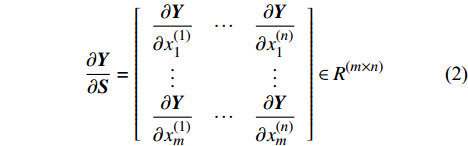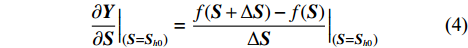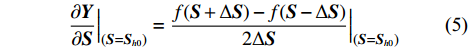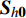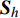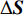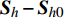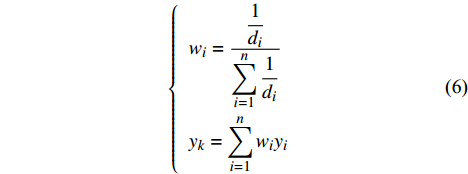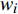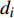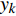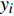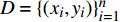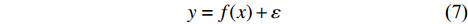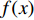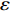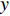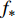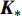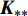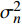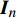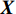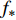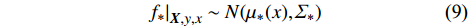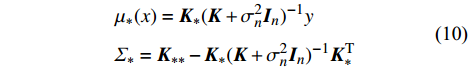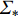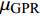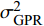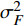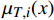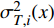Research on the data fusion algorithm based on flight test data and wind tunnel test data
-
摘要: 飞行试验受飞行轨迹和试验激励的限制，通过飞行遥测数据辨识得到的实飞气动数据只能分布于飞行轨迹上的少量特征段。风洞试验由于受地面模拟能力的限制，试验数据与实飞飞行数据存在一定的天地差异。为了弥补飞行试验辨识数据和风洞试验数据的“缺陷”，以一种典型轴对称飞行器为研究对象，对上述两种不同来源的气动数据进行数据融合方法研究。首先，通过气动力参数辨识方法得到飞行器沿实际飞行轨迹的六分量真实气动数据，然后比较与地面试验数据的差异性和一致性；最后分别采用基于梯度信息和基于高斯过程回归的数据融合方法对两种来源的气动数据进行融合。融合建模结果表明，两种融合模型预测数据均比单源模型精度更高；如果高、低精度数据的梯度信息较为一致，则基于梯度信息的数据融合方法效果更好；而基于高斯过程回归的数据融合方法能够给出融合数据的置信区间，有利于分析不确定度。Abstract: Due to the correlation between flight and ground test data, there is a certain difference between the wind tunnel test data and the flight test data. Limited by the flight trajectory and test excitation, the flight test data distributes in a small characteristic sections of the flight trajectory. And due to the limitation of ground simulation capabilities, wind tunnel tests have certain differences between the test data and the actual flight data. In order to remedy these limitations, researches of the data fusion algorithm based on above two different sources of aerodynamic data are conducted. Firstly, through the aerodynamic parameter identification method, the six-component real aerodynamic data of the aircraft along the actual flight trajectory are obtained, and then compare the difference and consistency with the wind tunnel test data. Finally, two kinds of data fusion methods based on gradient information and Gaussian process regression were used to fuse the two sources of aerodynamic datas. The results show that both the prediction data of the two fusion models are more accurate than the single source model; if the gradient information of the high and low precision data is more consistent, the data fusion method based on the gradient information is more effective; while the data fusion method based on the Gaussian process regression could obtain the confidence interval of the fusion data, which is useful to the analysis of uncertainty.
-
0. 引 言
在飞行器设计初期，需要基于气动数据进行多次反复迭代来确定和优化气动外形[1-2]。因此，如何获得精度高、不确定度小且代价低的气动数据成为了气动设计的关键点。
目前获得气动数据的手段主要有飞行试验、风洞试验和数值模拟[3-4]。现有飞行器的气动力建模主要是基于数值模拟或风洞试验数据[5-7]。风洞试验因为存在支架干扰、洞壁干扰和天地相关性等因素，与实际飞行数据存在一定差异，降低了气动力建模精度[8-9]；而飞行试验代价昂贵，受大气环境和传感器精度的影响较大，此外由于试验激励的限制，难以获得满足建模需求的辨识气动力数据样本。目前，国内外专门针对飞行试验数据进行建模的研究还较少。美国的Morelli等[10-11]进行了基于飞行试验数据的高效气动建模和基于飞行试验数据的气动模型参数准确性估计等一系列研究。国内王文正等[12]创新性地将数据挖掘技术应用于飞行试验数据分析和气动力参数辨识中，建立了基于飞行试验数据的建模方法、辨识结果一致性检验方法和舵效确认方法，对数值模拟和风洞试验数据的融合验证进行了初步探索。
从国内外研究内容来看，目前飞行试验数据主要用于气动建模和参数辨识等方面，用于气动数据融合方面的研究较少。基于此，本文提出了基于飞行试验数据和风洞试验数据的气动数据融合算法。飞行试验虽然获取的特征点数据少，但采用全尺寸飞行器可以获得真实飞行条件下的历程数据，数据更加真实，精度相比于风洞试验数据更高。可以用少量的飞行试验数据与风洞试验数据相融合，以达到提高数据精度同时降低试验代价的目的。本文以一种轴对称飞行器为研究对象，进行了基于梯度信息和基于高斯过程回归的气动力数据融合方法研究。该方法可更好地利用飞行试验数据，降低飞行试验次数和代价，提高气动力建模精度，研究结果有助于飞行器气动布局与控制系统设计。
1. 气动力数据样本
1.1 飞行试验数据样本
本文采用的轴对称飞行器进行了多次飞行试验，通过对遥测数据进行气动力参数辨识[13-14]，可以得到飞行器法向力系数
CN 、轴向力系数CA 和侧向力系数Cy 沿飞行时间的变化趋势，如图1所示。由图1可知，在飞行试验过程中，受操纵配平和机动能力的限制，飞行器主要在俯仰通道进行机动控制，侧向力气动力系数很小。在飞行末端，法向气动力系数变化相比于轴向力系数和侧向力系数更加明显，且末端轨迹落于低层大气中，大气测量手段更多，大气模型更加精确，有助于获得更加准确的飞行试验数据。所以末端法向力系数数据适合作为气动数据融合方法研究的高精度样本数据。
1.2 风洞试验数据样本
对象飞行器在风洞中进行了大量地面气动力试验，获取了较为完整的地面风洞试验数据集，并以此建立了飞行器气动力模型[15-16]。通过该模型，可以预测飞行包线内任意状态点的六分量气动力系数。
如图2所示，该飞行器采用“X”型尾翼布局，进行俯仰操纵时，四个舵的舵偏角存在
|δ1|=|δ4| 、|δ2|=|δ3| 关系。为降低气动力系数建模难度，同时考虑到飞行试验沿飞行轨迹状态的激励限制，采用俯仰通道舵偏δ1 、δ2 为变量、法向力系数CN 为研究样本对象。在特定飞行段，通常认为飞行试验辨识的气动力系数样本点精度较高、数量少；风洞试验数据气动力系数样本点数量多，但是由于存在天地相关性差异，精度较低。这里对上述两种来源的数据样本数量分别取5和60个特征状态点。在某一固定马赫数区域，通过Kriging建模[17-18]得到相应的响应面分布，如图3所示。两种数据样本在相同状态点的数值大小上表现出一定的差异性，但整体变化趋势表现出一致性。即两种来源的数据具有接近的梯度信息，反映了高超声速空气流动的基本物理规律。
2. 基于梯度信息的数据融合方法
2.1 算法原理
基于梯度信息的数据融合是最为朴素的一种数据融合算法。根据数据来源的不同，数据的变量是多维的，建立偏导数的阶数也可以是多阶的。阶数的增加会带来计算代价的大幅增加，这里考虑一般性和建模精度的要求，采用一阶偏导信息建立融合模型。已知有m个n维的样本点，它们的值及一阶偏导数信息如下：
数据样本：
\left\{ \begin{gathered} {{\boldsymbol{S}}} = \left[ {\begin{array}{*{20}{c}} {x_1^{(1)}}& \cdots &{x_1^{(n)}} \\ \vdots &{}& \vdots \\ {x_m^{(1)}}& \cdots &{x_m^{(n)}} \end{array}} \right] \in {R^{(m \times n)}} \\ {{\boldsymbol{Y}}} = \left[ {\begin{array}{*{20}{c}} {y_1^{(1)}}& \cdots &{y_1^{(n)}} \\ \vdots &{}& \vdots \\ {y_m^{(1)}}& \cdots &{y_m^{(n)}} \end{array}} \right] \in {R^{(m \times n)}} \end{gathered} \right. (1) 一阶导数：
\dfrac{{\partial {{\boldsymbol{Y}}}}}{{\partial {{\boldsymbol{S}}}}} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{\partial {\boldsymbol{Y}}}}{{\partial x_1^{(1)}}}}& \cdots &{\dfrac{{\partial {\boldsymbol{Y}}}}{{\partial x_1^{(n)}}}} \\ \vdots &{}& \vdots \\ {\dfrac{{\partial {\boldsymbol{Y}}}}{{\partial x_m^{(1)}}}}& \cdots &{\dfrac{{\partial {\boldsymbol{Y}}}}{{\partial x_m^{(n)}}}} \end{array}} \right] \in {R^{(m \times n)}} (2) 风洞试验数据多，可以较为准确地求得样本空间内任意位置处的一阶梯度。在任意高精度数据样本点处的融合气动力系数模型计算公式如下：
f({{{\boldsymbol{S}}}_h}) = f({{{\boldsymbol{S}}}_{h0}}) + \frac{{\partial {{\boldsymbol{Y}}}}}{{\partial {{\boldsymbol{S}}}}}({{{\boldsymbol{S}}}_h} - {{{\boldsymbol{S}}}_{h0}}) (3) \frac{{\partial {\boldsymbol{Y}}}}{{\partial {{\boldsymbol{S}}}}}\Big |_{{({{\boldsymbol{S}}} = {{{\boldsymbol{S}}}_{h0}})}} \Big. = \frac{{f({{\boldsymbol{S}}} + \Delta {{\boldsymbol{S}}}) - f({{\boldsymbol{S}}})}}{{\Delta {{\boldsymbol{S}}}}}\Big |_{{({{\boldsymbol{S}}} = {{{\boldsymbol{S}}}_{h0}})} }\Big. (4) \frac{{\partial {\boldsymbol{Y}}}}{{\partial {{\boldsymbol{S}}}}}\Big|_{ {({{\boldsymbol{S}}} = {{{\boldsymbol{S}}}_{h0}})} }\Big. = \frac{{f({{\boldsymbol{S}}} + \Delta {{\boldsymbol{S}}}) - f({{\boldsymbol{S}}} - \Delta {{\boldsymbol{S}}})}}{{2\Delta {{\boldsymbol{S}}}}}\Big|_{ {({{\boldsymbol{S}}} = {{{\boldsymbol{S}}}_{h0}})} }\Big. (5) 式中：
{{{\boldsymbol{S}}}_{{h}{\mathbf{0}}}} 为已知高精度样本点；{{{\boldsymbol{S}}}_{h}} 是预测数据点。式（4）和式（5）是两种求解梯度信息的方法，工程应用中一般采用后者。需注意的是，当求解梯度信息选用的距离\Delta {{\boldsymbol{S}}} 和样本值的距离{{{\boldsymbol{S}}}_h} - {{{\boldsymbol{S}}}_{h0}} 相同时，计算结果最精确。在预测过程中，若在整个样本空间的气动力模型是连续的，由一个高精度样本点及附近的一阶梯度信息可以求得所有需要的预测值。但在实际中，因为各种误差，气动力系数模型的一阶梯度是不连续的，会导致由多个高精度点计算得到的融合模型不光滑。
为了解决这一问题，本文创新性地设计了基于样本点相对距离的加权融合算法。如式（6）所示，对于新的预测点，首先计算它与所有已知高精度样本点的距离，并以距离为权值，对每个高精度样本点求得的预测值进行加权融合：
\left\{ \begin{array}{l} {w_i} = \frac{{\dfrac{1}{d_i}}}{{\displaystyle\sum\limits_{i = 1}^n {\dfrac{1}{d_i}} }} \\ {y_k} = \displaystyle\sum\limits_{i = 1}^n {{w_i}{y_i}} \end{array} \right. (6) 式中：
{w_i} 为第i个高精度样本点的权值，{d_i} 为预测点距离第i个高精度样本点的距离，{y_k} 为新的预测点的值，{y_i} 为单独使用1个高精度样本点求得的预测值。预测点距离样本点的距离越大则该样本点的影响越小，权值越低。这种方法既解决了融合模型不连续，也利用了所有已知样本点的建模信息，融合精度更高。2.2 数据融合结果
将高精度飞行试验数据随机分为训练集和验证集，用训练集与风洞试验数据进行融合，并用验证集进行验证，融合结果如图4所示。由图4可知，融合曲面具备与低精度数据回归曲面相同的变化趋势，并与高精度数据回归曲面部分重叠。融合模型综合利用了低精度数据的梯度信息和高精度数据的响应值信息，预测精度更加准确。
![]()
图 4 基于梯度信息的气动数据融合算法结果Figure 4. Results of aerodynamic data fusion algorithm based on gradient information利用验证集样本求得三种模型的均方根误差（root mean square error, RMSE）：仅利用低精度数据建立的回归模型预测均方根误差为7.012×10−2；仅利用高精度数据建立的回归模型预测均方根误差为1.632×10−2；基于梯度信息的气动数据融合模型预测均方根误差为7.125×10−3，数据融合模型具备更高的精度。
3. 基于高斯过程回归的数据融合方法
3.1 算法原理
高斯过程回归（Gaussian process regression, GPR）是一种基于贝叶斯优化的回归算法，对处理小样本、非线性、高维数等复杂问题具有良好的适用性[19-21]。在数据集合
D = \{ ({x_i},{y_i})\} _{i = 1}^n 中，考虑到噪声，高斯过程回归的一般模型为：y = f(x) + \varepsilon (7) 式中，
f(x) 为具有联合高斯分布的变量集合，\varepsilon 为高斯白噪声。根据贝叶斯原理，高斯过程回归在数据集D 建立了y 的先验函数，则样本点和新的数据点{f_*} 的后验分布为：\left[ \begin{gathered} y \\ {f_*} \\ \end{gathered} \right] \sim N\Bigg(0,\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{K}} + \sigma _n^2{{\boldsymbol{I}}_n}}&{{\boldsymbol{K}}_*^{\rm{T}}} \\ {{{\boldsymbol{K}}_*}}&{{{\boldsymbol{K}}_{**}}} \end{array}} \right]\Bigg) (8) 式中，N( )表示正态分布，
{\boldsymbol{K}} 为样本点之间对称正定的协方差矩阵，{{\boldsymbol{K}}_*} 为预测点与样本点之间的协方差矩阵，{{\boldsymbol{K}}_{**}} 为预测点自身的协方差，\sigma _n^2 为噪声的方差，{\boldsymbol I_n} 为单位矩阵。令
{\boldsymbol X} 为x的集合，由此计算得到预测值{f_*} 的后验概率分布为：\left. {{f_ * }} \right|_{{\boldsymbol{X}},y,x} \sim N({\mu _*}(x),{\varSigma _*}) (9) 式中：
\begin{gathered} {\mu _*}(x) = {{\boldsymbol{K}}_*}{({\boldsymbol{K}} + \sigma _n^2{{\boldsymbol{I}}_n})^{ - 1}}y \\ {\varSigma _*} = {{\boldsymbol{K}}_{ * * }} - {{\boldsymbol{K}}_ * }{({\boldsymbol{K}} + \sigma _n^2{{\boldsymbol{I}}_n})^{ - 1}}{\boldsymbol{K}}_ * ^{\rm{T}} \\ \end{gathered} (10) 即新的预测点均值和方差分别为
{\mu _*}(x) 和{\varSigma _*} 。采用基于高斯过程回归的气动数据融合算法对不同来源的气动数据进行融合，步骤如下：首先，对不同来源气动数据进行高斯过程回归处理，得到预测点的均值
{\mu _{{\text{GPR}}}} 和方差\sigma _{{\text{GPR}}}^{\text{2}} ，它反映了高斯回归模型的不确定度；接着，依据专家经验、试验经验等先验信息，设定数据源本身的保真度函数\sigma _F^2 ，它反映了样本的精度；然后将两者结合起来得到每一种数据源的总的不确定度\;{\mu _{T, i}(x)} 和\sigma _{T, i}^{\text{2}} (x) ；最后以不确定度方差作为权值进行融合。公式如下：\left\{ \begin{array}{l} {w_i} = \frac{{{ { { \dfrac{1} {\sigma _{T,i}^2(x)}} } }}}{{\displaystyle\sum\limits_{i = 1}^N {\dfrac{1}{\sigma _{T,i}^2(x)}} }} \\ \mu (x) = \displaystyle\sum\limits_{i = 1}^N {{w_i}} {\mu _{T,i}}(x) \\ {\sigma ^2}(x) = {\Bigg(\displaystyle\sum\limits_{i = 1}^N {\frac{1}{{\sigma _{T,i}^2(x)}}} \Bigg)^{ - 1}} \end{array} \right. (11) 3.2 数据融合结果
分别对飞行试验辨识气动力系数样本和风洞试验气动力系数样本进行高斯过程回归处理，得到每一种数据源的回归曲面和置信区间，如图5所示。由回归模型预测结果可知，对于低精度数据样本，数据样本点多，高斯过程回归模型的不确定度低，但是根据先验知识可知数据本身的准度较低，而高精度数据样本则与之相反。
![]()
图 5 单源气动数据高斯过程回归结果Figure 5. Single source aerodynamic data Gauss process regression results对两种来源数据分别进行高斯过程回归处理之后，采用基于不确定度的加权融合算法进行融合，结果如图6所示。融合数据曲面在数值上更接近于高精度数据回归曲面，并且融合之后的置信区间相比于单源数据直接建模结果更小，表明数据的不确定度更低。融合方法达到了提高数据精度、降低数据不确定度的目的。
![]()
图 6 基于高斯过程回归的气动数据融合结果Figure 6. Aerodynamic data fusion results based on Gaussian process regression4. 结 论
本文分别采用基于梯度信息和基于高斯过程回归的数据融合方法对飞行试验辨识数据和风洞试验数据进行融合，得到以下结论：
1）分析两种来源数据的差异性和一致性，两种数据样本在相同状态点的数值大小上表现出一定的差异性，但整体变化趋势表现出一致性。基于此，创新性地采用了基于梯度信息和基于高斯过程回归的两种融合算法对该飞行器气动力数据进行融合建模，结果均得到了比单源数据模型精度更高的融合模型。
2）创新地提出了一种以样本点相对距离作为权值的加权融合方法。当预测点距离样本点的距离越大，则该样本点的影响越小，权值越低。通过这种方法计算得到的预测值，解决了融合曲面不连续的问题，同时利用了所有已知的样本点，精度更高。
3）如果高、低数据的梯度信息较为一致，则基于梯度信息的数据融合适用性更高，预测结果更加准确；而基于高斯过程回归的数据融合方法不仅可以给出预测值，还可以分析置信区间，有利于不确定度的分析和研究。
-
![]()
图 4 基于梯度信息的气动数据融合算法结果
Figure 4. Results of aerodynamic data fusion algorithm based on gradient information
![]()
图 5 单源气动数据高斯过程回归结果
Figure 5. Single source aerodynamic data Gauss process regression results
-
[1] 杨勇, 张辉, 郑宏涛. 有翼高超声速再入飞行器气动设计难点问题[J]. 航空学报, 2015, 36(1): 49-57. YANG Y, ZHANG H, ZHENG H T. Difficulties in aerodynamic design problems of the winged hypersonic reentry vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 49-57. (in Chinese)
[2] 叶露. 变掠翼无尾飞机气动布局设计研究[J]. 飞行力学, 2019, 37(2): 36-40. YE L. Research of variable forward-sweep wing tailless aircraft aerodynamic configuration design[J]. Flight Dynamics, 2019, 37(2): 36-40. (in Chinese)
[3] 何开锋, 钱炜祺, 汪清, 等. 数据融合技术在空气动力学研究中的应用[J]. 空气动力学学报, 2014, 32(6): 777-782. doi: 10.7638/kqdlxxb-2014.0072 HE K F, QIAN W Q, WANG Q, et al. Application of data fusion technique in aerodynamics studies[J]. Acta Aerodynamica Sinica, 2014, 32(6): 777-782. (in Chinese) doi: 10.7638/kqdlxxb-2014.0072
[4] 王文正, 桂业伟, 何开锋, 等. 基于数学模型的气动力数据融合研究[J]. 空气动力学学报, 2009, 27(5): 524-528. doi: 10.3969/j.issn.0258-1825.2009.05.004 WANG W Z, GUI Y W, HE K F, et al. Aerodynamic data fusion technique exploration[J]. Acta Aerodynamica Sinica, 2009, 27(5): 524-528. (in Chinese) doi: 10.3969/j.issn.0258-1825.2009.05.004
[5] 何开锋, 王文正, 钱炜祺. 根据风洞试验结果建立有尾翼导弹数学模型[J]. 流体力学实验与测量, 2004, 18(4): 62-66. HE K F, WANG W Z, QIAN W Q. Mathematic modeling for the missile aerodynamics with tail- wing according to wind-tunnel test results[J]. Experiments and Measurements in Fluid Mechanics, 2004, 18(4): 62-66. (in Chinese)
[6] 赵清杰, 刘若宇. 基于随机森林的大迎角非线性非定常气动建模方法[J]. 北京理工大学学报, 2017, 37(11): 1171-1177. ZHAO Q J, LIU R Y. Modeling of aircraft nonlinear unsteady aerodynamics at high angle attack based on random forest[J]. Transactions of Beijing Institute of Technology, 2017, 37(11): 1171-1177. (in Chinese)
[7] 李富贵, 赵洪. 有限试验状态下面对称飞行器气动建模方法[J]. 固体火箭技术, 2016, 39(3): 417-421, 443. LI F G, ZHAO H. Modeling a plane-symmetric flight vehicle under limited states[J]. Journal of Solid Rocket Technology, 2016, 39(3): 417-421, 443. (in Chinese)
[8] 陈德华, 赵协和, 伍开元, 等. 小展弦比飞机非线性气动特性风洞与飞行相关性研究[J]. 空气动力学学报, 2002, 20(1): 72-77. doi: 10.3969/j.issn.0258-1825.2002.01.010 CHEN D H, ZHAO X H, WU K Y, et al. The correlation study of nonlinear aerodynamic characteristics of aircrafts with low aspect ratio[J]. Acta Aerodynamica Sinica, 2002, 20(1): 72-77. (in Chinese) doi: 10.3969/j.issn.0258-1825.2002.01.010
[9] 罗长童, 胡宗民, 刘云峰, 等. 高超声速风洞气动力/热试验数据天地相关性研究进展[J]. 实验流体力学, 2020, 34(3): 78-89. doi: 10.11729/syltlx20200006 LUO C T, HU Z M, LIU Y F, et al. Research progress on ground-to-flight correlation of aerodynamic force and heating data from hypersonic wind tunnels[J]. Journal of Experiments in Fluid Mechanics, 2020, 34(3): 78-89. (in Chinese) doi: 10.11729/syltlx20200006
[10] MORELLI E A, KLEIN V. Accuracy of aerodynamic model parameters estimated from flight test data[J]. Journal of Guidance, Control, and Dynamics, 1997, 20(1): 74-80. DOI: 10.2514/2.3997
[11] MORELLI E. Flight test maneuvers for efficient aerodynamic modeling[C]//Proc of the AIAA Atmospheric Flight Mechanics Conference, Portland, Oregon. Reston, Virigina: AIAA, 2011. doi: 10.2514/6.2011-6672
[12] 王文正, 郑鹍鹏, 陈功, 等. 数据挖掘技术在飞行试验数据分析和气动参数辨识中的应用研究[J]. 2016, 34(6): 778−782. WANG W Z, ZHENG K P, CHEN G, et al. Application research of data-mining method to flight test data analysis and aerodynamic parameter identification[J]. Acta Aerodynamica Sinica, 2016, 34(6): 778−782 (in Chinese).
[13] 杨媚, 王启, 何康乐. 无人机飞行试验参数辨识研究[J]. 飞行力学, 2017, 35(4): 77-80. YANG M, WANG Q, HE K L. UAV flight test parameter identification research[J]. Flight Dynamics, 2017, 35(4): 77-80. (in Chinese)
[14] 李善营, 高占宝, 刘紫阳, 等. 基于遥测数据的无人机气动参数辨识方法研究[J]. 飞行力学, 2017, 35(3): 32-36. LI S Y, GAO Z B, LIU Z Y, et al. Study on UAV's aerodynamic parameter identification method based on telemetry data[J]. Flight Dynamics, 2017, 35(3): 32-36. (in Chinese)
[15] 汪清, 何开锋, 钱炜祺, 等. 飞机大攻角空间机动气动力建模研究[J]. 航空学报, 2004, 25(5): 447-450. doi: 10.3321/j.issn:1000-6893.2004.05.004 WANG Q, HE K F, QIAN W Q, et al. Aerodynamic modeling of spatial maneuvering aircraft at high angle of attack[J]. Acta Aeronautica et Astronautica Sinica, 2004, 25(5): 447-450. (in Chinese) doi: 10.3321/j.issn:1000-6893.2004.05.004
[16] 黄达, 郑万祥. 基于风洞试验的非定常气动力微分方程建模方法[J]. 南京航空航天大学学报, 2014, 46(4): 599-602. doi: 10.3969/j.issn.1005-2615.2014.04.017 HUANG D, ZHENG W X. Unsteady aerodynamic modeling method using differential equations based on wind tunnel test[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2014, 46(4): 599-602. (in Chinese) doi: 10.3969/j.issn.1005-2615.2014.04.017
[17] 韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197-3225. HAN Z H. Kriging surrogate model and its application to design optimization: a review of recent progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225. (in Chinese)
[18] 李宝玉, 张磊刚, 裘群海, 等. 基于Kriging模型梯度解析解的改进一次二阶矩方法[J]. 航空学报, 2019, 40(5): 222629. LI B Y, ZHANG L G, QIU Q H, et al. An advanced first order and second moment method based on gradient analytical solution of Kriging surrogate model[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(5): 222629. (in Chinese)
[19] 孙斌, 姚海涛, 刘婷. 基于高斯过程回归的短期风速预测[J]. 中国电机工程学报, 2012, 32(29): 104-109, 5. SUN B, YAO H T, LIU T. Short-term wind speed forecasting based on Gaussian process regression model[J]. Proceedings of the CSEE, 2012, 32(29): 104-109, 5. (in Chinese)
[20] SEEGER M. Gaussian processes for machine learning[J]. International Journal of Neural Systems, 2004, 14(2): 69-106. DOI: 10.1142/s0129065704001899
[21] 何志昆, 刘光斌, 赵曦晶, 等. 高斯过程回归方法综述[J]. 控制与决策, 2013, 28(8): 1121-1129, 1137. HE Z K, LIU G B, ZHAO X J, et al. Overview of Gaussian process regression[J]. Control and Decision, 2013, 28(8): 1121-1129, 1137. (in Chinese)
-
期刊类型引用(5)
1. 马洪强，王圣友，王苏宁，王骁. 运动模型式飞行器气动力参数测试系统研究. 计算机测量与控制. 2024(05): 88-93+101 . 
百度学术
2. 王润，刘晋，张青青，尹琰鑫，屈强. 高马赫数气动热环境数据融合方法与展望. 空天技术. 2024(03): 33-41 . 百度学术
3. 王旭，宁晨伽，王文正，张伟伟. 面向飞行试验的多源气动数据智能融合方法. 空气动力学学报. 2023(02): 12-20 . 本站查看
4. 于海森，王长亮，谭述君，刘玉玺，胡迪科. 运载火箭姿态控制多速率陀螺融合方法. 上海航天(中英文). 2023(01): 144-149 . 百度学术
5. 刘汉宇，张耘隆，张津泽，胡彦辰，袁赫. 基于风洞试验数据和仿真融合修正的气动特性预示技术. 导弹与航天运载技术(中英文). 2023(02): 97-101+136 . 百度学术
其他类型引用(2)
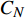
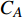
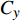
下载:
计量
- 文章访问数: 648
- HTML全文浏览量: 157
- PDF下载量: 155
- 被引次数: 7
