态-态模型下的CO<sub>2</sub>系统热非平衡过程数值研究

段欣葵; 曾明; 王辉; 王东方

doi:10.7638/kqdlxxb-2023.0140

态-态模型下的CO₂系统热非平衡过程数值研究

国防科技大学空天科学学院，长沙　410073

基金项目: 国家自然科学基金（11927803）

详细信息

作者简介:
段欣葵（2001—），女，湖南永州人，硕士研究生，研究方向：高温气体动力学. E-mail：duan_xk@163.com

通讯作者:
曾明^*（1971—），女，湖南娄底人，教授，研究方向：高温气体动力学. E-mail: ming_z@163.com

中图分类号: V211.22
计量
- 文章访问数: 322
- HTML全文浏览量: 21
- PDF下载量: 48
出版历程
- 收稿日期: 2023-08-28
- 修回日期: 2023-11-08
- 录用日期: 2023-11-21
- 网络出版日期: 2023-12-07
- 发布日期: 2023-12-10
- 刊出日期: 2024-06-24

Numerical study of thermal nonequilibrium process in CO₂ system with state-to-state model

College of Aerospace Science and Engineering, National University of Defense Technology, Changsha　410073, China

摘要

摘要:
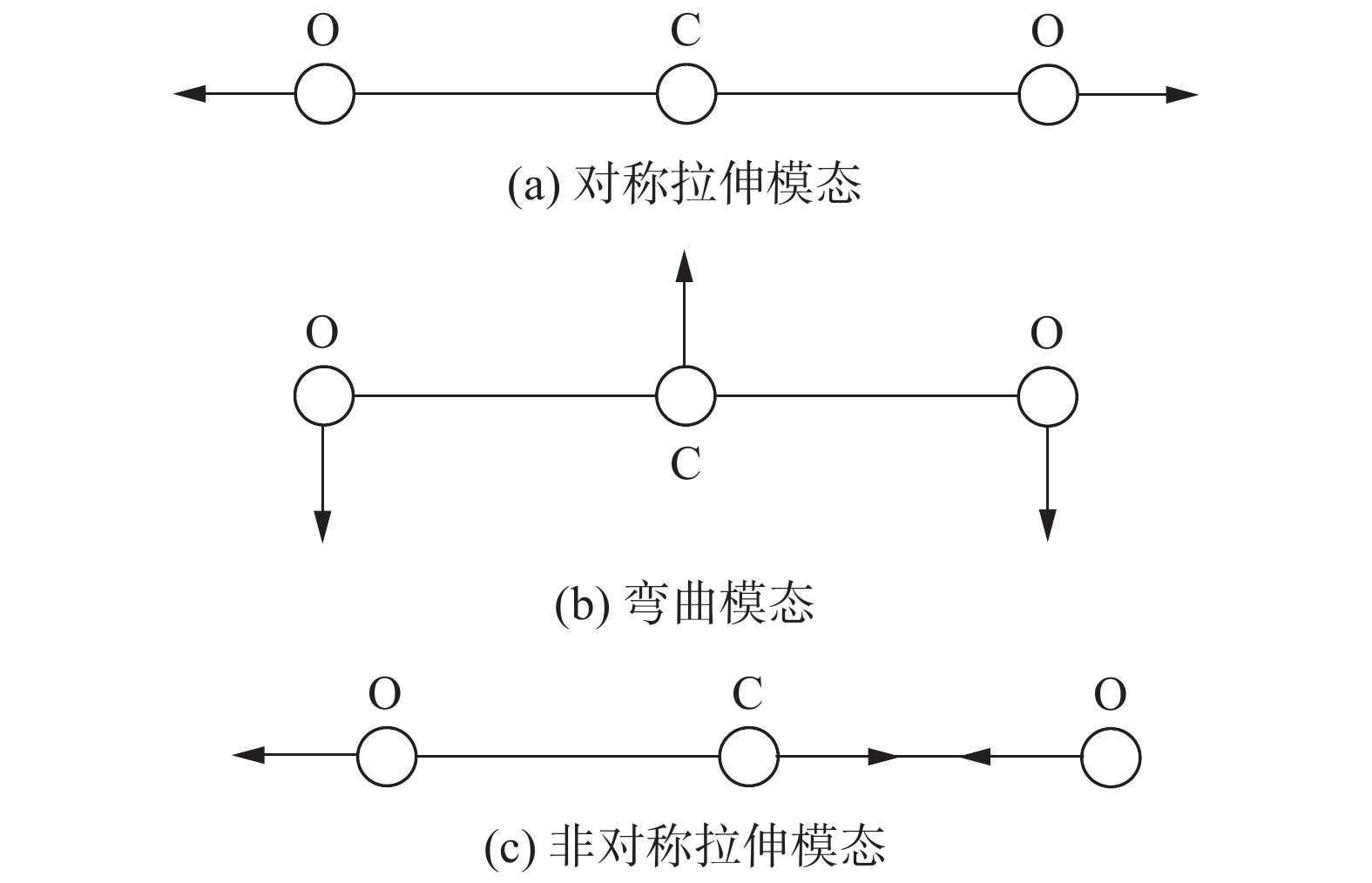
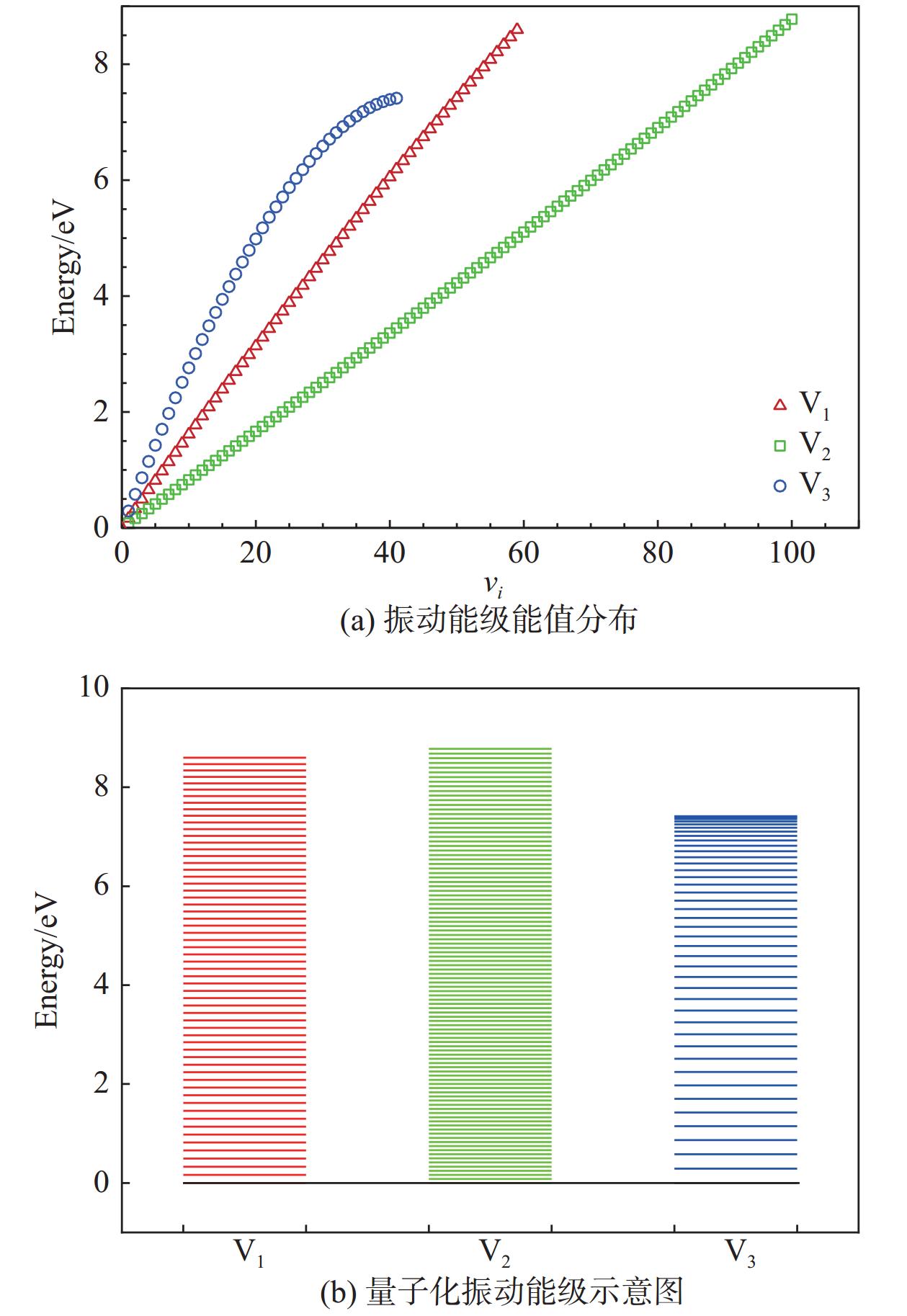
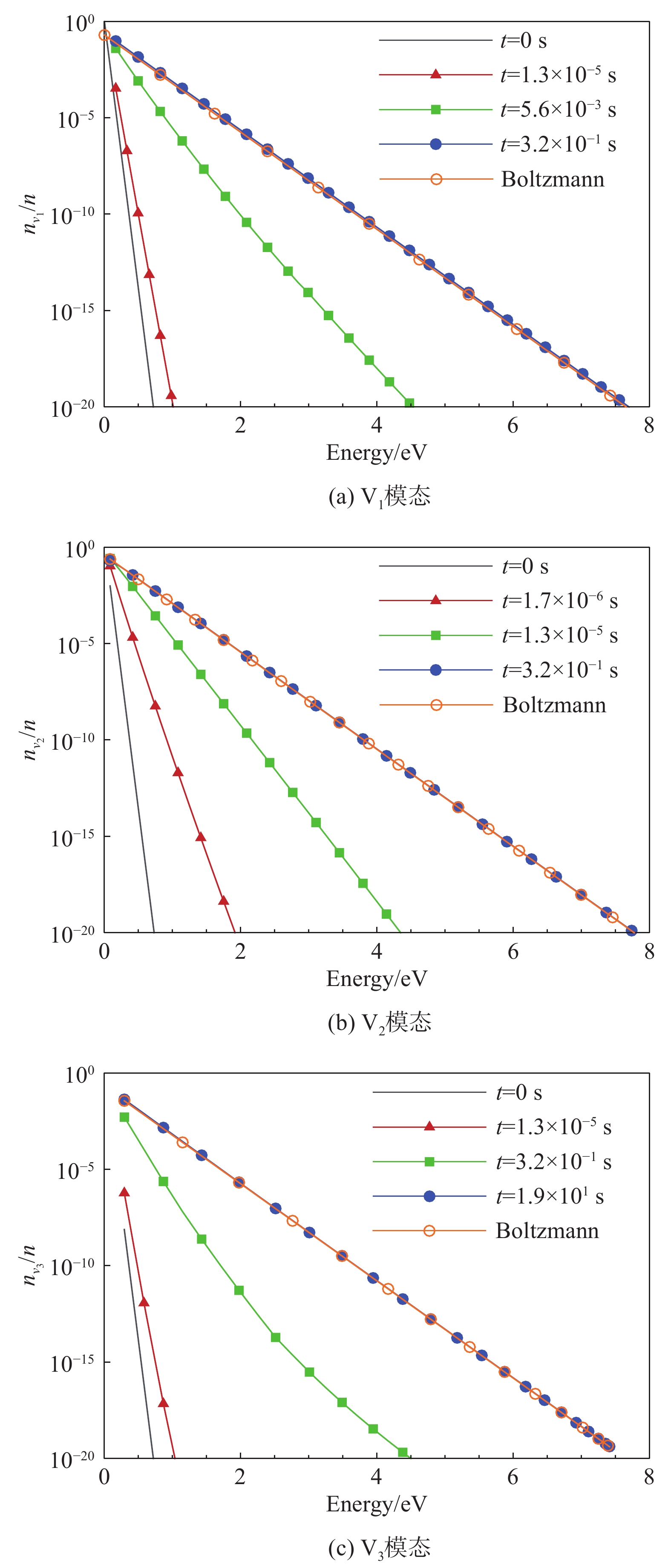
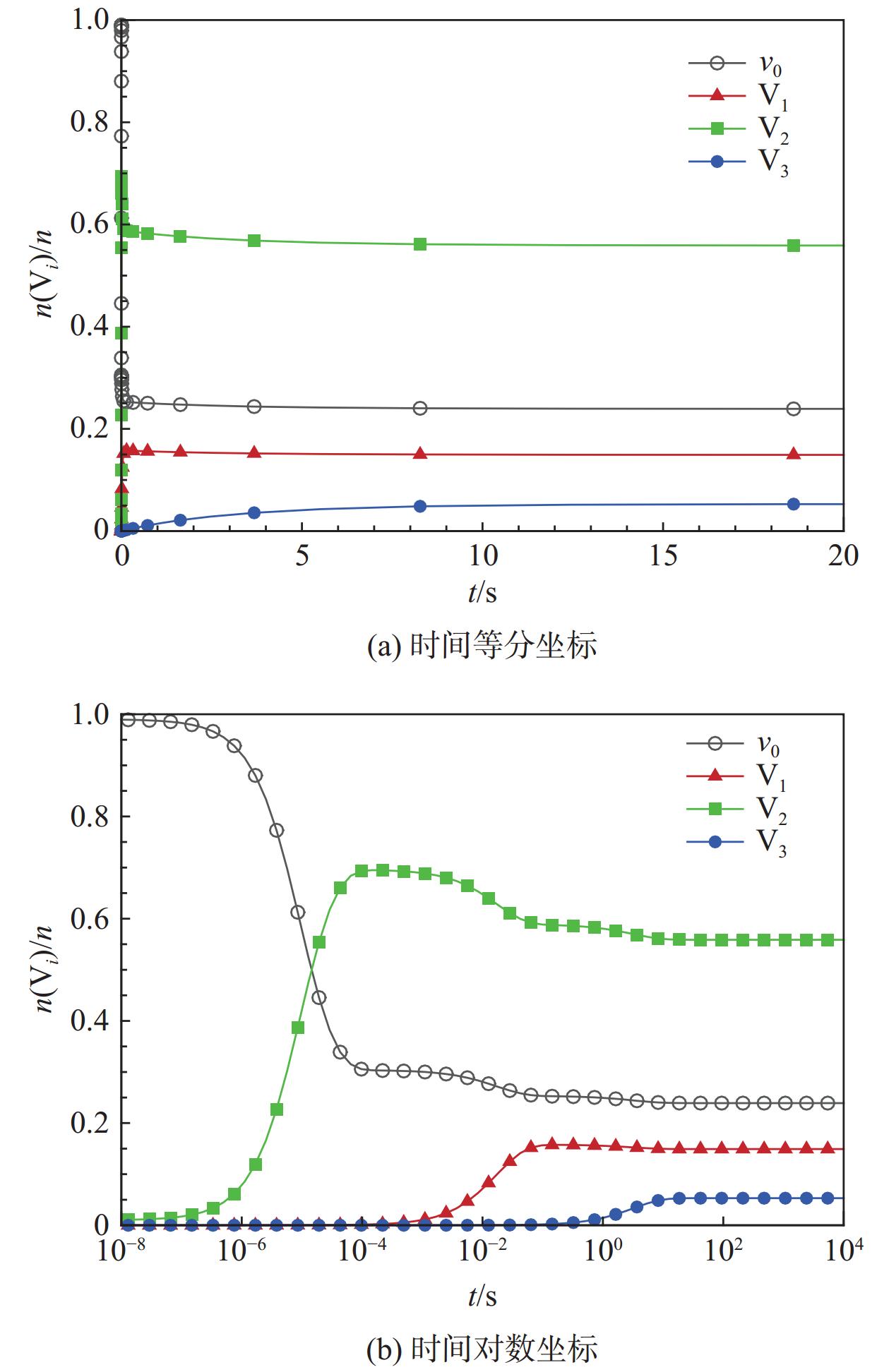
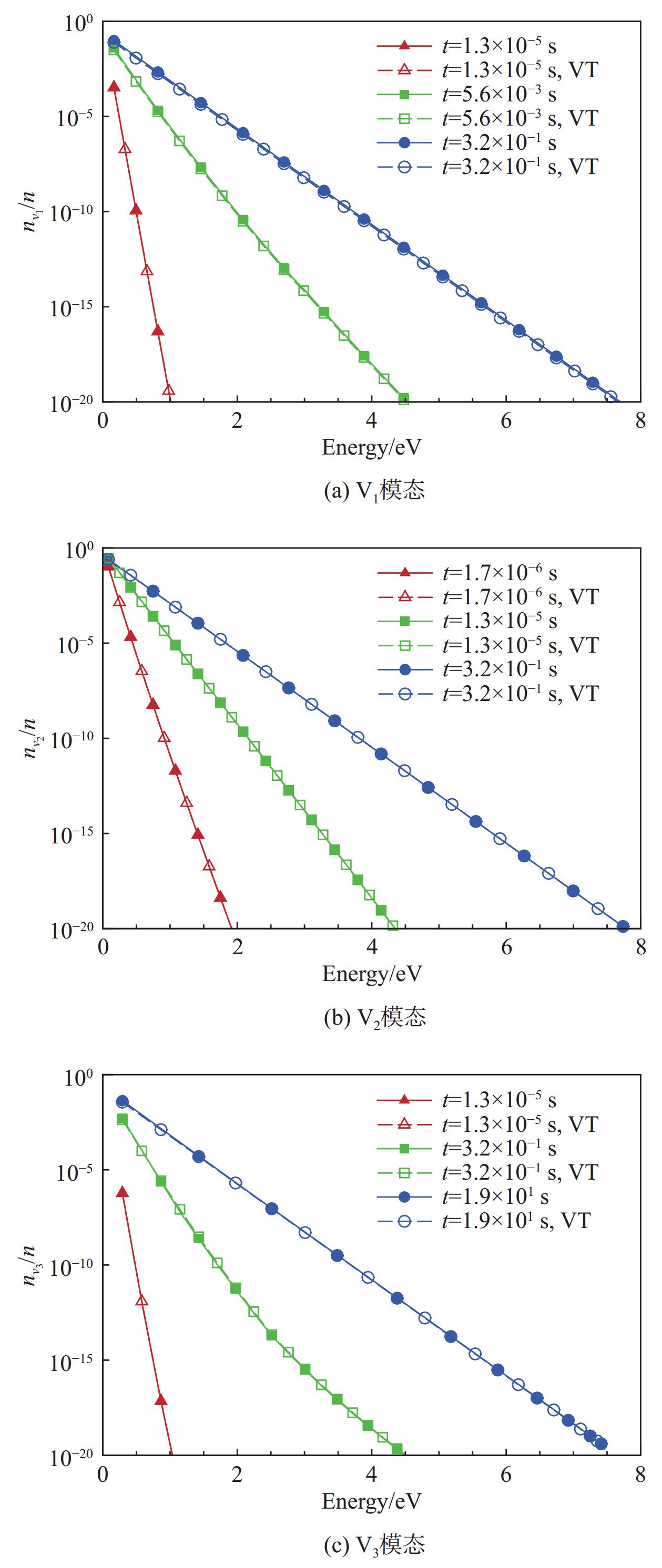
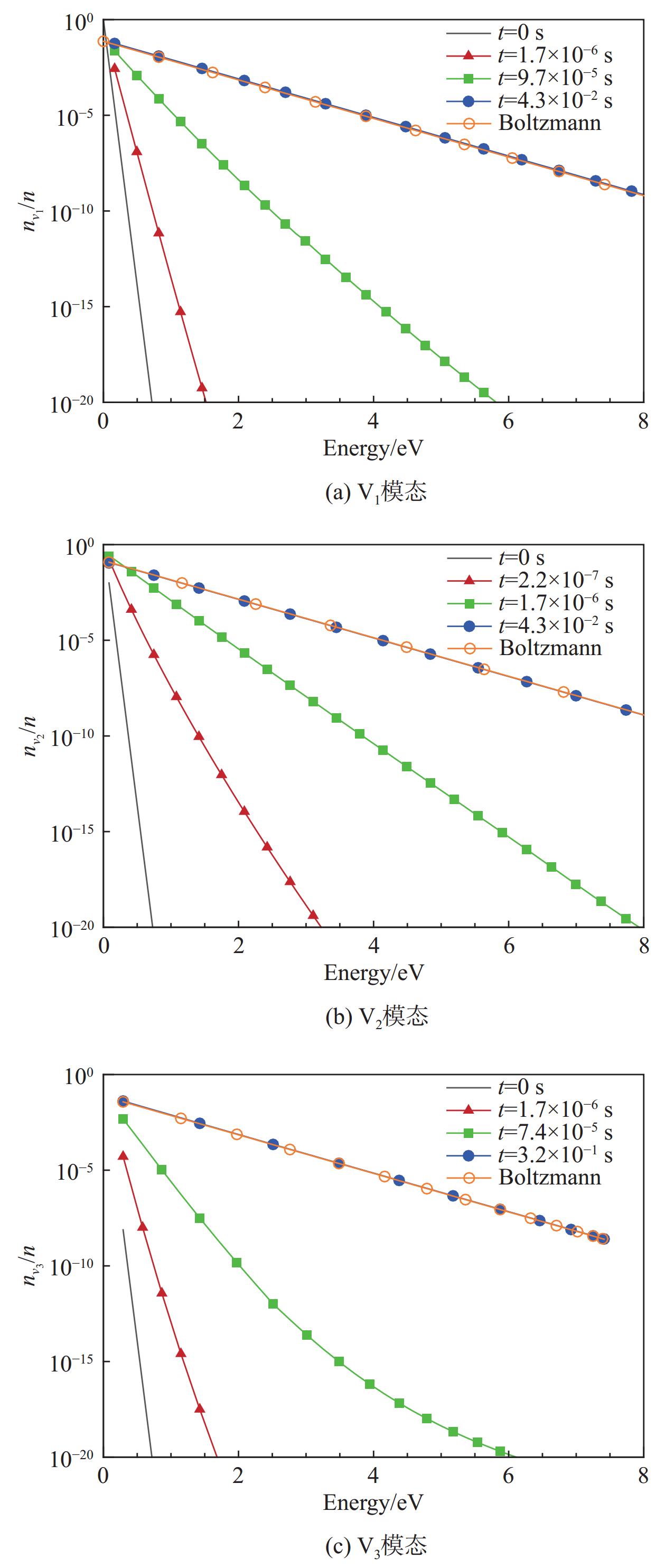
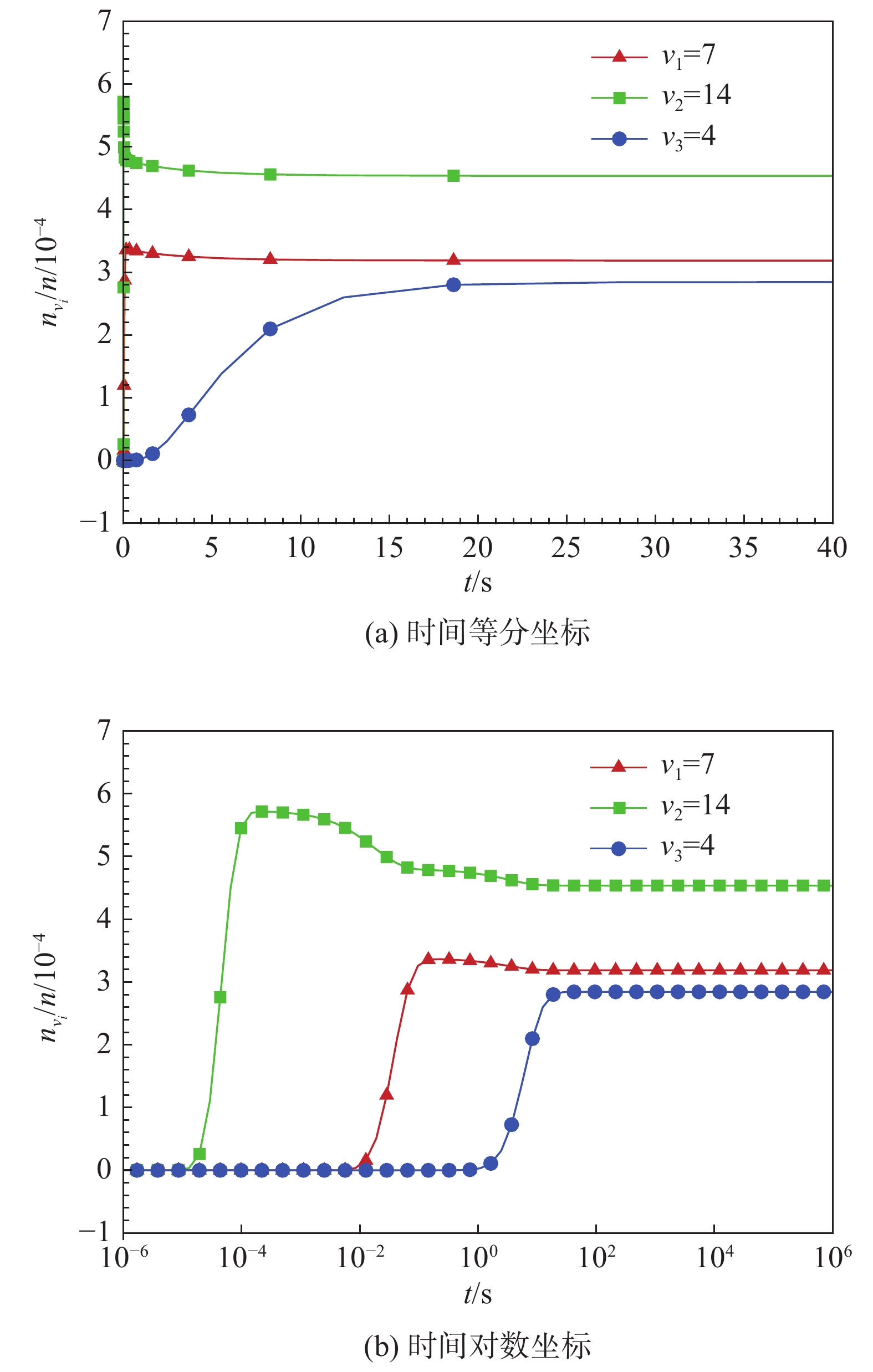
以火星大气条件下飞行器非平衡流场研究为背景，采用态-态模型对定容静止CO₂系统自30 km火星大气条件（181 K）瞬时升温后的热非平衡过程开展数值模拟。考虑CO₂分子的对称拉伸、弯曲和非对称拉伸三个振动模态共201个振动能级，微观过程包括：振动-平动（VT）能量交换过程引起的同一模态内部的和不同模态间的振动能级跃迁，振动-振动（VV）能量交换过程引起的同一模态内部振动能级跃迁。分析不同振动模态的能级分布演化特点，并考察对应微观过程细节探究内在原因，结果表明：VT过程起支配作用，对由初始低温突然升温后保持定温的气体非平衡过程，VV过程的贡献可以忽略；CO₂分子的弯曲振动模态具有最快的激发速率，平衡时也具有最高的粒子数占比，升温至2000 K情况下，对称拉伸和非对称拉伸模态的松弛时间约为弯曲模态的2.2倍和46.1倍；更高温度下振动能级跃迁速率加大，升温至5000 K情况达到平衡的平均松弛时间比2000 K情况低了2个量级。
- 热非平衡 /
- 态-态模型 /
- CO₂ /
- 数值模拟 /
- 振动能级分布
Abstract:
With the background of research on nonequilibrium flow field outside Mars probe, the thermal nonequilibrium process after temperature increase of a stationary CO₂ system from Martian atmospheric condition at an altitude of 30 km (181 K) is studied with state-to-state model. The system with initial condition of Martian atmosphere is heated suddenly to a high temperature and then is kept at constant temperature and volume. Three vibrational modes (symmetric stretching, bending and asymmetric stretching modes) and totally 201 vibrational energy levels are considered. The microscopic processes include: vibration-translation (VT) energy exchange processes that cause transitions between energy levels of the same or different modes, vibration-vibration (VV) energy exchange processes that cause transitions within the same mode. The time evolution of vibrational distribution for the three modes and the specifics of the corresponding microscopic processes are analyzed. The results show that: (1) VT processes are dominant, the contribution of VV processes can be ignored for such sudden increase and then constant temperature case. (2) Among the three vibrational modes, the bending mode has the fastest excitation rate and the largest equilibrium population. For the case of temperature rise to 2000 K, the relaxation time for the symmetric and asymmetric stretching modes is respectively about 2.2 times and 46.1 times of that for the bending mode. (3) As the transition rates increase with temperature, the average relaxation time for 5000 K case is lower than that for 2000 K by two orders of magnitude.
- thermal nonequilibrium /
- state-to-state model /
- carbon dioxide /
- numerical simulation /
- vibrational population distribution

HTML全文

图 9 升温至T = 2000 K和T = 5000 K两种情况下三种模态粒子数占比随时间的变化

Figure 9. Particle population fractions of three modes under two temperature conditions

下载: 全尺寸图片幻灯片

图 1 CO₂的3种振动模态

Figure 1. Three vibration modes of CO₂

下载: 全尺寸图片幻灯片

图 2 CO₂分子三种模态振动能级图

Figure 2. Vibrational energy levels in three modes of CO₂

下载: 全尺寸图片幻灯片

图 3 非平衡过渡过程中若干时刻的振动能级分布（T = 2000 K）

Figure 3. Vibration energy level distributions at several moments in nonequilibrium transient process (T = 2000 K)

下载: 全尺寸图片幻灯片

图 4 三种模态粒子数占比随时间的变化（T = 2000 K）

Figure 4. Proportion of particle population in three modes (T = 2000 K)

下载: 全尺寸图片幻灯片

图 5 三种模态具有相近振动能的能级松弛过程对比（T = 2000 K）

Figure 5. Comparison of relaxation process of vibrational levels with similar energy in three modes (T = 2000 K)

下载: 全尺寸图片幻灯片

图 6 有无VV过程作用的若干时刻振动能级分布对比（T = 2000 K）

Figure 6. Comparison of vibration energy level distribution with or without VV process at several moments in nonequilibrium transient process (T = 2000 K)

下载: 全尺寸图片幻灯片

图 7 向v₁ = 1与v₂ = 2两个振动能级（振动能约为0.165 eV）的跃迁过程

Figure 7. Transitions to v₁ = 1 and v₂ = 2 with vibration energy about 0.165 eV

下载: 全尺寸图片幻灯片

图 8 非平衡过渡过程中若干时刻的振动能级分布（T = 5000 K）

Figure 8. Vibration energy level distribution at several moments in nonequilibrium transient process (T = 5000 K)

下载: 全尺寸图片幻灯片

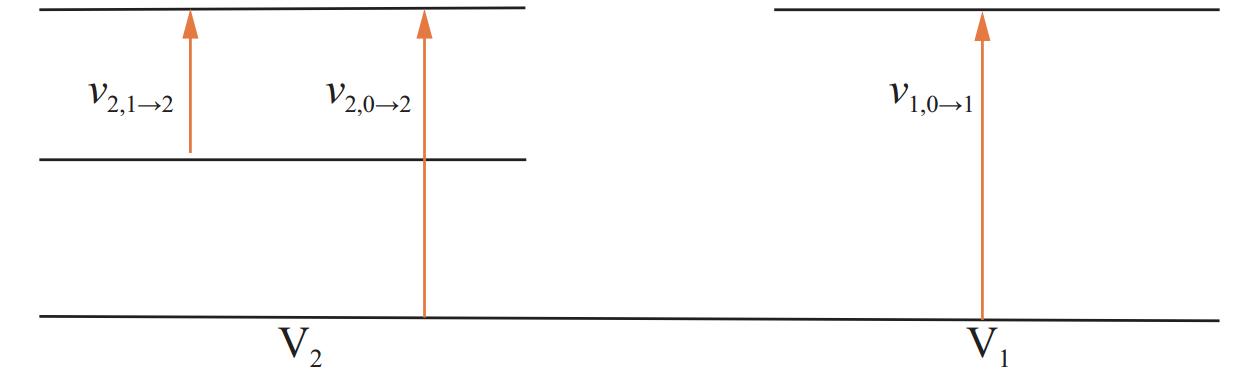
表 1 初始时刻V₁和V₂模态粒子数密度（T = 2000 K）

Table 1 Population of V₁ and V₂ modes at the initial moment (T = 2000 K)

State	$n_{{v_i}}^0$ /m^–3
v₀	1.20×10²³
v₁ = 1	2.99×10¹⁸
v₂ = 1	1.19×10²¹
v₂ = 2	5.90×10¹⁸

下载: 导出CSV

表 2 初始时刻V₁和V₂模态跃迁速率（T = 2000 K）

Table 2 Transition rates of V₁ and V₂ modes at the initial moment (T = 2000 K)

Process	k_f /（m³·s^–1）	k_b /（m³·s^–1）	${{{\text{d}}{n_{{v_i}}}} \mathord{\left/ {\vphantom {{{\text{d}}{n_{{v_i}}}} {{\text{d}}t}}} \right. } {{\text{d}}t}}$ /（m^–3·s^–1）	Total ${{{\text{d}}{n_{{v_i}}}} \mathord{\left/ {\vphantom {{{\text{d}}{n_{{v_i}}}} {{\text{d}}t}}} \right. } {{\text{d}}t}}$ /（m^–3·s^–1）
${v_{{1_{}}(0 \to 1)}}$	2.87×10^–22	–7.49×10^–22	4.18×10²⁴	4.18×10²⁴
${v_{{2_{}}(0 \to 2)}}$	2.85×10^–21	–3.73×10^–21	4.15×10²⁵	2.12×10²⁶
${v_{{2_{}}(1 \to 2)}}$	1.19×10^–18	–1.93×10^–18	1.71×10²⁶	2.12×10²⁶
注：k_f表示正向跃迁速率系数，k_b表示逆向跃迁速率系数。

下载: 导出CSV

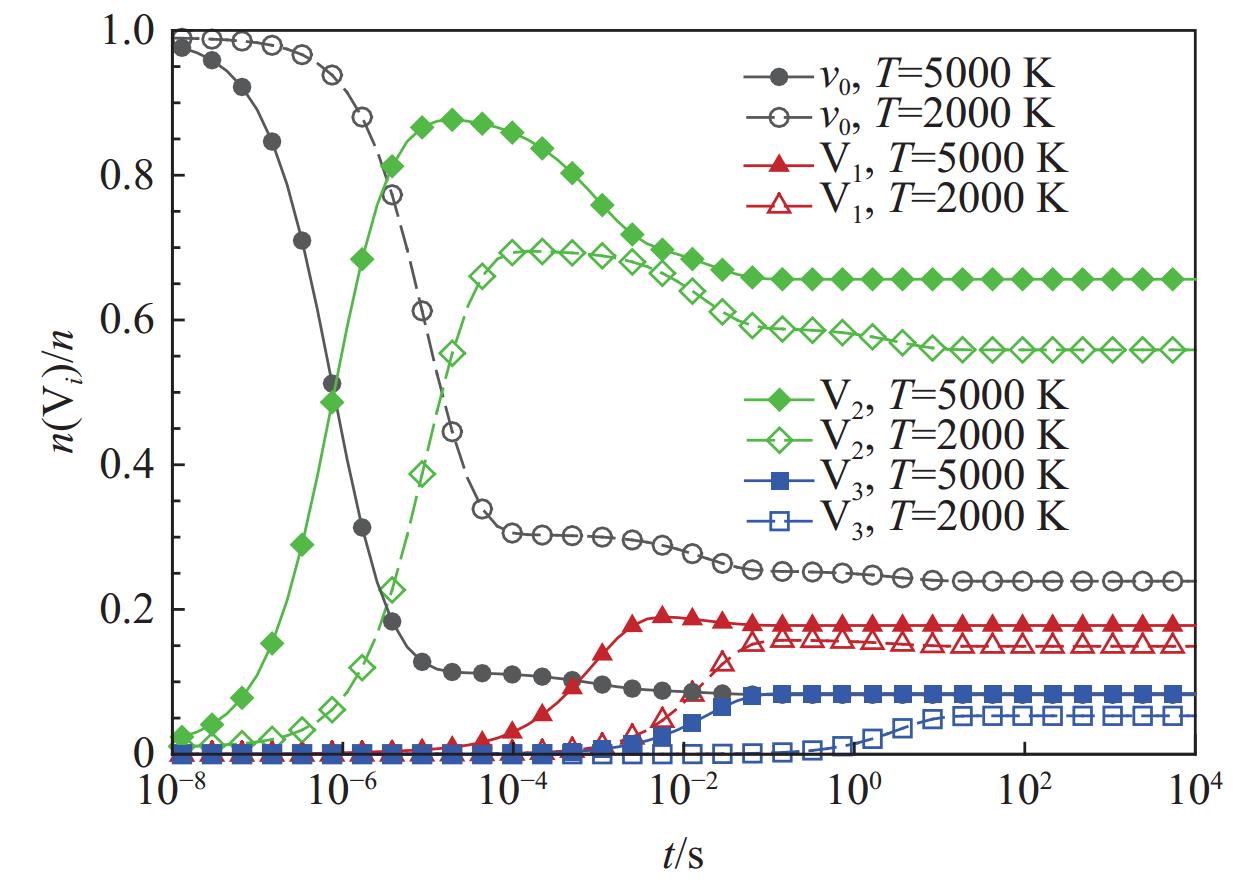
表 3 升温至T = 2000 K和T = 5000 K两种情况下平衡时基态及三种模态粒子数占比

Table 3 Fractions of equilibrium particle population in ground state and three modes under two temperature conditions

T/K	${n_{{v}_0}}\Big/n$	${n_{{\mathrm{V}}_1}}\Big/n$	${n_{{\mathrm{V}}_2}}\Big/n$	${n_{{\mathrm{V}}_3}}\Big/n$
2000	23.9%	14.9%	55.9%	5.3%
5000	8.2%	17.8%	65.6%	8.4%

下载: 导出CSV

参考文献(26)

[1]	唐伟, 杨肖峰, 桂业伟, 等. 火星进入器高超声速气动力/热研究综述[J]. 宇航学报, 2017, 38(3): 230−239. doi: 10.3873/j.issn.1000-1328.2017.03.002 TANG W, YANG X F, GUI Y W, et al. Review of hypersonic aerodynamics and aerothermodynamics for Mars entries[J]. Journal of Astronautics, 2017, 38(3): 230−239(in Chinese). doi: 10.3873/j.issn.1000-1328.2017.03.002
[2]	COLONNA G, ARMENISE I, BRUNO D, et al. Reduction of state-to-state kinetics to macroscopic models in hypersonic flows[J]. Journal of Thermophysics and Heat Transfer, 2006, 20(3): 477−486. doi: 10.2514/1.18377
[3]	徐丹, 曾明, 张威, 等. 态-态模型下N₂/N混合物的热化学非平衡过程研究[J]. 空气动力学学报, 2014, 32(3): 280−288. doi: 10.7638/kqdlxxb-2012.0139 XU D, ZENG M, ZHANG W, et al. Thermo-chemical nonequilibrium process in N₂/N mixture with state-to-state model[J]. Acta Aerodynamica Sinica, 2014, 32(3): 280−288(in Chinese). doi: 10.7638/kqdlxxb-2012.0139
[4]	徐丹, 曾明, 张威, 等. 采用态-态模型的热化学非平衡喷管流数值研究[J]. 计算物理, 2014, 31(5): 531−538. doi: 10.3969/j.issn.1001-246X.2014.05.004 XU D, ZENG M, ZHANG W, et al. Numerical study of thermochemical nonequilibrium nozzle flow in state-to-state model[J]. Chinese Journal of Computational Physics, 2014, 31(5): 531−538 (in Chinese). doi: 10.3969/j.issn.1001-246X.2014.05.004
[5]	郑伟杰, 曾明, 王东方, 等. 态-态模型下的O₂/O系统热化学非平衡与辐射过程[J]. 空气动力学学报, 2020, 38(3): 448−460. doi: 10.7638/kqdlxxb-2019.0087 ZHENG W J, ZENG M, WANG D F, et al. Numerical study of thermo-chemical nonequilibrium and radiation process for O₂/O system with state-to-state approach[J]. Acta Aerodynamica Sinica, 2020, 38(3): 448−460 (in Chinese). doi: 10.7638/kqdlxxb-2019.0087
[6]	王辉, 曾明, 段欣葵, 等. 高温空气正激波流动的态-态模型与多温度模型对比研究[C]//第二十届全国计算流体力学会议论文集. 哈尔滨, 2023: 932-944. WANG H, ZENG M, DUAN X K, et al. Comparative study of state-to-state model and multi-temperature model on normal shock wave flow in high-temperature air[C]//20th Computational Fluid Mechanics, Harbin 2023: 932-944 (in Chinese).
[7]	PARK C, HOWE J T, JAFFE R L, et al. Review of chemical-kinetic problems of future NASA missions. II - Mars entries[J]. Journal of Thermophysics and Heat Transfer, 1994, 8(1): 9−23. doi: 10.2514/3.496
[8]	KUSTOVA E V, NAGNIBEDA E A. On a correct description of a multi-temperature dissociating CO₂ flow[J]. Chemical Physics, 2006, 321(3): 293−310. doi: 10.1016/j.chemphys.2005.08.026
[9]	KUSTOVA E V, NAGNIBEDA E A. Kinetic model for multi-temperature flows of reacting carbon dioxide mixture[J]. Chemical Physics, 2012, 398: 111−117. doi: 10.1016/j.chemphys.2011.05.019
[10]	ARMENISE I, REYNIER P, KUSTOVA E. Advanced models for vibrational and chemical kinetics applied to Mars entry aerothermodynamics[J]. Journal of Thermophysics and Heat Transfer, 2016, 30(4): 705−720. doi: 10.2514/1.t4708
[11]	KUSTOVA E, MEKHONOSHINA M. Novel approach for evaluation of CO₂ vibrational relaxation times[J]. Chemical Physics Letters, 2021, 764: 138288. doi: 10.1016/j.cplett.2020.138288
[12]	杨肖峰, 国义军, 唐伟, 等. 进入火星大气的高温真实气体效应与气动加热研究[J]. 宇航学报, 2018, 39(9): 959-967. YANG X F, GUO Y J, TANG W, et al. High-temperature real-gas effects and aerodynamic heating for capsules entering Martian atmosphere[J]. Journal of Astronautics, 2018, 39(9): 959-967(in Chinese).
[13]	刘庆宗, 董维中, 丁明松, 等. 火星探测器气动热环境和气动力特性的数值模拟研究[J]. 空气动力学学报, 2018, 36(4): 642−650. doi: 10.7638/kqdlxxb-2016.0053 LIU Q Z, DONG W Z, DING M S, et al. Numerical simulation of aerothermal environments and aerodynamic characteristics for Mars entry capsules[J]. Acta Aerodynamica Sinica, 2018, 36(4): 642−650(in Chinese). doi: 10.7638/kqdlxxb-2016.0053
[14]	杨星链, 王京盈, 郝佳傲, 等. PHAROS求解火星进入热化学非平衡流场的测试及应用[J]. 航空科学技术, 2022, 33(7): 86−94. doi: 10.19452/j.issn1007-5453.2022.07.010 YANG X L, WANG J Y, HAO J A, et al. Test and application of PHAROS solver for simulating thermo-chemical nonequilibrium flow of Mars entry[J]. Aeronautical Science & Technology, 2022, 33(7): 86−94(in Chinese). doi: 10.19452/j.issn1007-5453.2022.07.010
[15]	JAE GANG KIM, SUNG MIN JO. Modification of chemical-kinetic parameters for 11-air species in re-entry flows[J]. International Journal of Heat and Mass Transfer, 2021, 169: 120950. doi: 10.1016/j.ijheatmasstransfer.2021.120950
[16]	KUNOVA O, KOSAREVA A, KUSTOVA E, et al. Vibrational relaxation of carbon dioxide in state-to-state and multi-temperature approaches[J]. Physical Review Fluids, 2020, 5(12): 123401. doi: 10.1103/physrevfluids.5.123401
[17]	ARMENISE I, KUSTOVA E V. State-to-state models for CO₂ molecules: from the theory to an application to hypersonic boundary layers[J]. Chemical Physics, 2013, 415: 269−281. doi: 10.1016/j.chemphys.2013.01.034
[18]	KUSTOVA E V, NAGNIBEDA E A. State-to-state theory of vibrational kinetics and dissociation in three-atomic gases[J]. AIP Conference Proceedings, 2001, 585(1): 620−627. doi: 10.1063/1.1407618
[19]	洪启臻. 高温热化学非平衡流动的精细模拟研究[D]. 北京: 中国科学院大学, 2022.
[20]	SCHWARTZ R N, SLAWSKY Z I, HERZFELD K F. Calculation of vibrational relaxation times in gases[J]. The Journal of Chemical Physics, 1952, 20(10): 1591−1599. doi: 10.1063/1.1700221
[21]	VARGAS J, LOPEZ B, LINO DA SILVA M. Heavy particle impact vibrational excitation and dissociation processes in CO₂[J]. The Journal of Physical Chemistry A, 2021, 125(2): 493−512. doi: 10.1021/acs.jpca.0c05677
[22]	PIETANZA L, GUAITELLA O, AQUILANTI V, et al. Advances in non-equilibrium CO₂ plasma kinetics: a theoretical and experimental review[J]. The European Physical Journal D, 2021, 75(9): 237. doi: 10.1140/epjd/s10053-021-00226-0
[23]	MÁRIO LINO DA SILVA. The STELLAR database[DB/OL]. 2020-07-14[2023-07-15]. http://esther.ist.utl.pt/pages/stellar.html.
[24]	BROWN P N, BYRNE G D, HINDMARSH A C. VODE: a variable-coefficient ODE solver[J]. SIAM Journal on Scientific and Statistical Computing, 1989, 10(5): 1038−1051. doi: 10.1137/0910062
[25]	SCHOFIELD J T, BARNES J R, CRISP D, et al. The Mars pathfinder atmospheric structure investigation/meteorology (ASI/MET) experiment[J]. Science, 1997, 278(5344): 1752−1758. doi: 10.1126/science.278.5344.1752
[26]	ARMENISE I, KUSTOVA E. Mechanisms of coupled vibrational relaxation and dissociation in carbon dioxide[J]. The Journal of Physical Chemistry A, 2018, 122(23): 5107−5120. doi: 10.1021/acs.jpca.8b03266