0.   引言

飞船返回舱等高超声速飞行器在大气层中飞行时，头部前方空气经激波强烈压缩而急剧升温，并将发生离解、电离等化学反应，产生相应原子和离子。而飞行器表面材料往往对流场中的原子、离子具有催化复合作用，使其在飞行器表面附近发生复合反应形成相应分子，由此改变飞行器表面附近的组分分布。另一方面，催化复合反应是一种放热过程，它也会改变飞行器表面附近流场的温度分布。显然这两方面因素都将直接影响飞行器的气动热环境。这一现象已被美国NASA航天飞机防热瓦催化特性飞行试验所证实^[1]。因此研究壁面催化对飞行器热环境影响规律，发展壁面催化条件下气动热环境精确预测方法对高超声速飞行器热防护系统设计和可靠性验证具有重大意义。

对于高超声速飞行器，壁面催化反应往往发生在高温非平衡流动中。受地面设备能力及经费的限制，目前难以依靠地面或飞行试验系统研究壁面催化对飞行器气动热环境影响。地面试验主要用于研究材料的催化特性，为催化计算建模和校核提供依据^[2]。随着CFD技术的发展和计算机硬件能力的提升，CFD数值模拟已成为解决存在壁面催化等高温热化学非平衡效应条件下高超声速飞行器气动热环境预测的重要手段^[3]。在CFD方法中，通常以催化边界条件的形式模拟壁面催化效应，即需给出壁面上的组分分布。完全非催化和完全催化是两种最容易实现的催化边界条件，其中完全非催化假定壁面附近组分分布不存在梯度，壁面组分分布等于流场内点组分分布；而完全催化认为流场中的原子、离子在壁面完全复合，在冷壁条件下，可认为壁面组分与来流组分分布相同(超级催化)。由于完全非催化条件下壁面组分分布梯度为零，不会形成扩散热流，故完全非催化壁条件下的热流计算结果将低于完全催化壁^[4]。但实际上，壁面一般处于有限催化状态，上述两种极限情况只能用于定性分析。因此要实现高超声速飞行器气动热环境精确预测，必须采用有限催化边界条件。

根据催化反应速率常数的计算方法，有限催化边界条件可分为两类^[5]：一是指定催化效率(催化复合系数)，再根据催化效率计算催化反应速率常数^[6]；二是采用壁面有限速率化学反应动力学方法，对气固复相催化反应过程进行分析和建模，直接计算催化反应速率常数^[7]，得到催化反应速率常数后，再根据表面质量守恒原理确定壁面各组分分布，即实现了有限催化边界条件。由于第一种实现方法相对简单，且有大量防热材料催化系数实验数据的支持^[8-10]，因此得到了广泛的应用。

返回舱等飞行器再入过程中将因电离反应形成等离子体鞘套，严重时还会导致通讯黑障，因此壁面处也会发生离子组分的催化反应。而目前已发表的研究工作主要是针对氧原子、氮原子以及碳原子等中性原子的有限催化反应^[11-13]，存在离子组分时壁面有限催化对气动加热的影响规律还不清晰。为此本文首先采用指定催化效率的方法，发展了包含离子组分的有限催化边界条件，并结合多组分化学非平衡N-S方程数值求解，建立了有限催化条件下的高超声速飞行器气动热环境计算方法。然后针对类联盟号飞船返回舱外形，采用7组分电离空气化学模型和有限催化边界条件对其典型再入工况气动热环境开展了计算分析，研究了存在离子组分时其气动热环境随壁面催化效率的变化规律，并对壁面有限催化影响气动加热的物理机制进行了探讨。

1.   计算方法

1.1   流动控制方程

本文旨在考察分子离解、电离以及催化复合等现象对气动热环境的影响，因此只考虑了化学非平衡效应，暂时不模拟热力学非平衡和辐射等现象。流动控制方程为三维守恒形式的多组分化学非平衡气体N-S方程组^[14]：

式中，Q为守恒变量，S_r为化学反应源项，F、G、H为无黏通量，F^v、G^v、H^v为黏性通量。采用采用有限体积法，在网格控制体单元内对控制方程进行积分，结合Gauss定理，得：

式中，Σ和n分别为控制体单元表面面积和外法向单位向量，V为控制体单元体积。f=Fi+Gj+Hk和f^v=F^vi+G^vj+H^vk分别是无黏和黏性通量矢量。

黏性应力张量、热流矢量、组分质量扩散通量分别满足牛顿应力关系、傅里叶热传导定律和费克扩散定律这些线性输运本构关系。对飞行器的气动加热由下式计算：

式中，Q_c、Q_d分别为热传导和组分扩散对总气动加热的贡献，可称为传导热流和扩散热流。

本文采用了7组分Dunn-Kang^[15]电离空气模型, 组分比焓h_s等热力学函数由多项式拟合给出^[16]，黏性系数、热传导系数及扩散系数等输运系数的具体计算方法可参考文献[17]。

1.2   有限催化边界条件

在CFD数值模拟中，壁面催化效应通常以催化边界条件的形式出现，即需给出壁面上的组分分布。下面以7组分电离空气为例，给出包含离子组分的有限催化边界条件。

高温空气包含离子组分时，壁面催化反应可包括原子复合和离子复合两种类型。对7组分电离空气，考虑如下3个催化复合反应：

由催化反应引起的单位时间，单位面积壁面上组分质量消耗为：

式中，k_s为催化反应速率常数，ρ_w为壁面处密度，f_ws为壁面处组分质量分数，负号表示质量损失。

给定催化效率后，壁面无滑移时k_s可由下式计算^[18]：

式中γ_s为催化效率，也被称为催化复合系数。它等于在壁面发生催化复合的原子数与入射到壁面总原子数之比。显然其取值在0到1之间，取0时表示完全非催化，取1时表示完全催化。

中性分子为催化反应的生成物，根据质量守恒原理，催化反应引起的壁面单位面积组分质量增加为：

式中，M_NO、M_NO⁺为对应组分的摩尔质量。另一方面，壁面处由扩散作用产生的质量通量为：

其中n为壁面法向单位矢量，方向由壁面指向流场内部。壁面无质量引射时，各组分单位时间单位面积由催化反应产生(消耗)的质量与扩散出(到)飞行器表面的质量应相等，即各组分在壁面处的净质量通量为零。故下述关系式成立：

由于边界条件中涉及组分质量分数的壁面法向导数，实际计算时还需要恰当离散。本文综合计算效率和计算稳定性两方面考虑，发展了一种近似隐式处理方法：壁面组分质量分数采用隐式离散，其它系数项采用显示离散。例如，s=N, O, NO⁺时，式(9)可离散为：

式中，上标n表示用第n时间步的量计算，dn为壁面第一层网格中心到壁面的距离，f_1s为该处组分质量分数。流场迭代计算时，已知n时间步流场变量后，根据下式更新壁面组分质量分数：

其他组分处理方法类似，不再赘述。在给定催化效率后，由前述关系式可以确定所有重粒子组分在壁面的分布，最后再根据电中性假设得出电子在壁面的质量分数。

1.3   求解方法

对控制方程进行无量纲化处理后，采用有限体积法进行离散。为了克服刚性问题，同时兼顾计算稳定性和计算效率，对无黏项和化学反应源项采用隐式格式离散，而黏性项的离散采用显式二阶中心格式离散。最后采用LU-SGS方法^[19]进行时间推进求解，并使用局部时间步长加速收敛。为解决复杂外形网格生成困难问题，采用了多块结构网格MPI分区并行求解技术。

气动热计算好坏关键在于能否准确模拟边界层，特别是壁面附近的温度梯度、组分质量分数梯度。高超声速流场中含有强激波等间断，如果计算格式耗散太小可能引起计算发散或出现红玉现象等非物理解，而计算格式耗散太大又会影响边界层的刻画，最终都不能得到好的热流计算效果。因此要想准确计算热流，需要在激波处引入适当耗散以稳定激波，同时在边界层内要尽量减小耗散。为解决这一问题，本文在流场变量梯度大的方向(壁面法向)采用耗散小的Godunov格式^[20]，而在流场变量梯度小的方向采用耗散大的Steger-Warming矢通量分裂格式^[21]，以提高计算鲁棒性，同时不降低热流计算精度^[22]。

对于边界条件的处理，壁面可采用无滑移完全非催化/催化，以及有限催化边界条件，壁面温度可按等温壁设定或由辐射平衡关系计算。由于非规则外形流场存在激波/激波, 激波/边界层干扰现象，通常使用的壁面法向零压力梯度条件不一定适用，故本文采用由内点外插的方法计算壁面压力。超声速来流边界则直接采用来流条件，对于超声速出口边界采用一阶外插的方法。

2.   方法验证

标模ELECTRE几何外形是半锥角为4.6°的球锥体，头部半径为0.175 m，弹身总长为2.0 m，且拥有飞行试验测热数据^[23]。其中发射后第293 s时刻(高度53.3 km，迎角近似为0°，马赫数13)公开报道的热流数据最完整，包含沿标模母线所有测点数据；且该工况飞行速度在4000 m/s以上，高温气体效应已不能忽略；加之飞行高度在50 km以上，可以避免转捩及湍流模拟，更易于考察高温气体效应。基于上述原因，已有大量文献把ELECTRE第293 s时刻工况作为高温非平衡流场及气动热计算方法的考核算例。本文为验证所建方法和计算程序的可靠性，也对该算例进行了考核计算。计算时壁面温度取为343 K, 且采用了完全非催化和完全催化两种壁面催化条件。

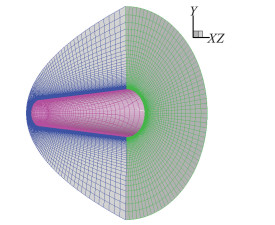
网格分布，特别是壁面法向网格间距对气动热计算影响较大^[24]。为考核计算方法对气动热计算的网格无关性，并由此确定合适的壁面法向网格间距，共划分了Rec=1、5、10、20、50五种不同网格雷诺数的计算网格。网格雷诺数的定义如下：

式中，ρ_∞、V_∞、μ_∞分别为自由来流密度、速度和黏性系数，Δn为壁面法向第一层网格间距。为同时验证程序的三维问题计算能力，五套网格均为三维网格，且拓扑结构一致，壁面法向网格数均为81，如图 1所示。

图  1  网格拓扑结构

Figure  1.  The topology of mesh used in simulation

下载: 全尺寸图片 幻灯片

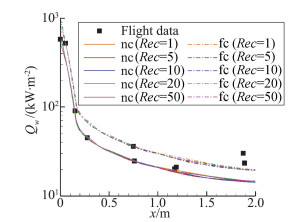
图 2给出了不同网格和壁面催化条件下ELECTRE弹身母线热流密度计算结果与飞行试验数据比较情况。图例中“nc”表示壁面为完全非催化，“fc”表示壁面为完全催化。本文的计算方法具有较好的网格无关性，网格雷诺数小于20后热流计算结果基本相同。热流分布规律计算与试验基本一致，除尾部外飞行试验数据处于完全非催化壁和完全催化壁预测结果之间。

图  2  计算与飞行试验结果比较

Figure  2.  Comparison among the CFD results and Flight data

下载: 全尺寸图片 幻灯片

3.   返回舱热环境计算分析

利用上节所述计算方法，对类联盟号飞船返回舱气动热环境开展了数值计算。由于返回舱通常采用碳基或硅基防热材料，其催化效率通常小于0.1，因此本文只考虑了0.0、0.02、0.05、0.1四种壁面催化效率，且假设各组分的催化效率相同。计算工况高度为70 km，马赫数为24.9，迎角为30°，壁面温度为350 K。由于该工况飞行高度较高，均按层流流态计算。

图 3是返回舱流场温度分布云图。返回舱激波压缩强烈，过激波后流场温度急剧升高，并在返回舱大底、迎风面与弓形激波之间形成了高温区。与量热完全气体总静关系式估计结果比较，波后温度明显降低，可以预见波后高温激波层内发生离解等吸热化学反应。这一点可从图 4给出的流场组分质量分数云图得到证实：过激波后O₂分子和N₂分子发生离解并生成相应O原子与N原子，因此原子质量分数明显增加而对应分子质量分数显著下降。此外流场中还生成了NO分子，并进一步电离产生了NO⁺离子，因此有必要研究包含离子组分时有限催化对返回舱气动加热的影响。

图  3  返回舱流场温度云图

Figure  3.  Temperature contour of capsule flowfield

下载: 全尺寸图片 幻灯片

图  4  组分质量分数云图

Figure  4.  Mass fraction contours

下载: 全尺寸图片 幻灯片

图 5给出了不同催化效率条件下返回舱表面热流密度分布情况。当催化效率等于零，即完全非催化壁时热流密度最低；随着催化效率增大，返回舱迎风面热流密度明显增加。可见壁面有限催化对气动加热有重要影响。采用低催化效率的防热材料可有效缓和返回舱气动热环境。

图  5  返回舱表面热流密度云图

Figure  5.  Heat-flux contour of capsule surface

下载: 全尺寸图片 幻灯片

驻点是返回舱热环境最为严酷的部位，图 6给出了返回舱驻点峰值热流随壁面催化效率的变化情况。如图 6所示，在本文考虑的范围内，返回舱驻点总热流和扩散热流均随着催化效率单调递增，但热流增加率并不是线性，而是随催化效率逐渐减小。扩散热流对催化效率更加敏感，且量值上可以超过传导热流。此外通过比较总热流与扩散热流的变化规律可以看出，在驻点区域，催化效应主要通过扩散机制影响气动加热。

图  6  返回舱驻点热流密度比较

Figure  6.  Heat-flux contour of capsule surface

下载: 全尺寸图片 幻灯片

除驻点外，返回舱大底也是气动加热严重的部位，为分析有限催化对其热环境的影响，图 7给出了不同催化效率条件下沿大底中心线的热流密度分布情况。可以看出有限催化条件下热流密度明显升高，但中心线不同位置处热流密度随催化效率的变化规律不尽相同：驻点附近区域热环境受催化作用影响显著，热流密度随催化效率的绝对增幅也最大；而在远离驻点的流动膨胀区，催化效率大于0.02后热流密度变化不大。

图  7  返回舱大底中心线热流密度分布

Figure  7.  Heat-flux distribution along the center line of capsule 's base

下载: 全尺寸图片 幻灯片

为进一步厘清壁面有限催化对气动热环境的影响机制，图 8和图 9分别给出了沿返回舱大底中心线的传导热流和扩散热流密度分布。壁面催化效率大于0.02后，传导热流基本不受壁面催化效率影响，而且量值上反而低于完全非催化壁。而扩散热流受壁面催化系数影响明显，这再次说明有限催化条件下，扩散热流是影响气动加热的主要机制。

图  8  返回舱大底中心线传导热流密度分布

Figure  8.  Conductive heat-flux distribution along the center line of capsule's base

下载: 全尺寸图片 幻灯片

图  9  返回舱大底中心线扩散热流密度分布

Figure  9.  Diffusive heat-flux distribution along the center line of capsule's base

下载: 全尺寸图片 幻灯片

从物理上分析，催化效率反映了原子、离子在壁面发生催化复合反应的强弱，对壁面及壁面附近组分质量分数分布有直接影响。由扩散热流表达式(3)可以看出，扩散热流与壁面法向组分质量分数梯度直接相关，因此对催化效率更加敏感。另一方面催化复合反应属于放热反应，对壁面附近温度梯度也会产生影响。但从本文计算结果看，这种影响相对较小，与壁面温度梯度直接相关的传导热流对催化效率并不敏感。这两方面原因共同造成了传导与扩散热流的相对大小会随催化效率发生变化。同时也说明壁面催化效应主要是通过原子、离子在壁面发生催化复合反应，改变壁面及壁面附近组分分布，进而导致扩散热流发生变化，对总气动加热产生影响。

需要指出的是，在驻点附近区域和远离驻点区域，催化效率对扩散热流的影响规律明显不同。驻点附近扩散热流随催化效率增大而增大，而在远离驻点的流动膨胀区扩散热流则可能随催化系数增大反而减小。这说明壁面催化对气动加热的影响不仅与表征材料催化能力的催化效率有关。

从CFD计算的角度看，催化等效于改变了壁面边界条件，并由此改变了流场及热流。为分析具体哪些因素决定了催化效率的影响，可以从有限催化边界条件推导过程分析。以原子离子组分为例，由式(5)和式(6)不难得到，催化反应引起的单位时间，单位面积壁面上质量消耗${{{\dot{m}}}_{s}}$是催化效率、壁面密度、壁面温度和壁面组分质量分数的函数：

壁面处由扩散作用产生的质量通量为$J_{s}^{D}={{\rho }_{w}}{{D}_{ws}}{{\left( \frac{\partial {{f}_{s}}}{\partial n} \right)}_{w}}$，式中扩散系数D_ws由壁面温度和组分质量分数确定，因此有

最后根据组分在壁面处的净质量通量为零，即${{{\dot{m}}}_{s}}$+J_s^D=0，由此确定f_ws的隐函数：

考虑到实际计算中，壁面法向组分梯度是以离散形式计算，即：

f_sⁱⁿ为内部流场组分质量分数，显然与流场的离解电离程度相关。

通过上述分析，我们可以得到如下初步推论：壁面有限催化对气动热的影响不仅与壁面材料催化效率有关，也与流场离解电离程度、壁面密度、温度等当地流动参数相关。这也解释了本文返回舱算例中，在驻点附近区域和远离驻点区域，催化效率对热流的影响规律明显不同的原因。

4.   结论

初步建立了包含离子组分有限催化条件下的高超声速飞行器气动热环境计算方法和软件。针对类联盟号飞船返回舱外形，研究了壁面有限催化对其气动热环境的影响规律，主要结论如下：

1) 表征材料催化能力的催化效率对气动加热影响显著，随着催化效率增大，返回舱迎风面热流密度明显增加。采用低催化效率壁面材料可有效缓和返回舱气动热环境。

2) 催化作用主要通过扩散机制影响气动加热。扩散热流对壁面催化效率更加敏感，且量值上可以超过传导热流，但热流并不随催化效率增加而线性增大。

3) 催化作用对气动加热的影响不仅与壁面材料催化效率本身有关，也与流场离解电离程度、壁面密度、温度等当地流动参数相关。

本文的工作假定了所有催化反应的催化效率都为相同常数，且只考虑了0.1以下的催化效率，因此所得结论还需要进一步研究确认。本文采用了等温壁条件，没有研究壁温对催化的影响。而实际上催化效率与壁面温度是密切相关的，在以后的研究中应考虑随壁温变化的催化效率模型。另外对烧蚀热防护系统，壁面氧化、氮化反应也对气动热环境有重要影响，因此除壁面催化反应外，还需要发展同时考虑其它壁面反应的边界条件。

热力学非平衡现象如振动-化学反应耦合，会改变相关反应的化学反应速率，并由此对流场组分分布造成影响。而壁面催化主要是通过组分扩散机制影响气动加热，对流场组分分布相对敏感，因此有必要评估热力学非平衡效应对壁面催化气动加热的影响。本文作者针对此问题已开展了初步研究，结果表明：对返回舱大底这类大钝头体外形，飞行速度在第一宇宙速度以下时，热力学非平衡效应对其气动热环境影响较小，不会改变本文的研究结论，相关情况将另文详细探讨。