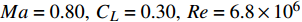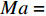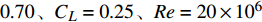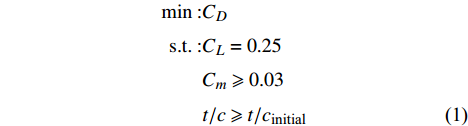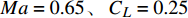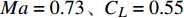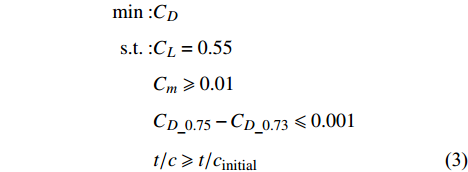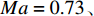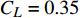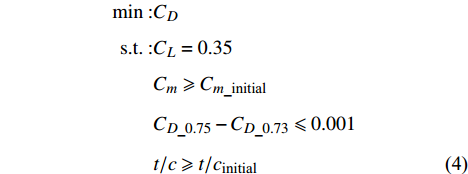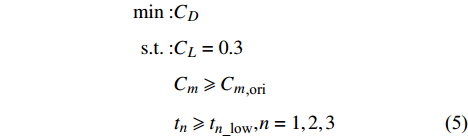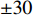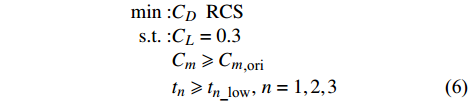A multi-disciplinary global/local optimization method for flying-wing airfoils design
-
摘要: 针对飞翼无尾布局飞机开展了基础翼型研究。归纳了飞翼布局翼型的设计特点和研究进展，提炼了飞翼无尾布局复杂的气动设计需求，总结了其展向气动分布特点，根据不同分区提出了翼型气动设计要求，并建立了分区翼型设计模型，形成了飞翼布局分区翼型系列。由于传统翼型设计模型未能考虑横流效应，导致翼型设计结果应用到三维布局上不能达到理想效果，提出了“全局+局部”的翼型多学科设计方法，根据飞翼布局分区翼型气动设计要求，建立了基于分区翼型设计模型的高效代理模型全局优化设计与三维布局环境下多剖面翼型局部优化设计的多学科协同设计方法。这种“全局+局部”的设计方法能够快速实现满足飞翼布局分区多剖面、多种性能要求的翼型设计，有效提高了设计翼型的性能与设计效率。最后以类X47-B布局为例，进行了翼型系列设计，验证了该方法的可靠性。
-
关键词:
- 飞翼布局 /
- 分区翼型设计模型 /
- 翼型系列设计 /
- 三维环境设计 /
- "全局+局部"多学科设计
Abstract: This paper proposes a new design method for aircrafts with flying-wing layouts. Aerodynamic characteristics and design requirements of flying-wing layouts are firstly analyzed. Aerodynamic design requirements for different spanwise partitions of flying wings are then put forward for the design of partitioned airfoils. Since traditional airfoil design methods do not take the cross-flow effect into account, their applications in designing three-dimensional airfoil layouts cannot achieve desired performance. Consequently, a global/local airfoil multidisciplinary design method is proposed. According to aerodynamic design requirements of flying wings, an efficient proxy model based on partitioned airfoils for global optimization design and a refined local optimization design method for three-dimensional layouts are established and integrated. This multi-disciplinary collaborative global/local optimization method can quickly realize the airfoil design that meets the performance requirements of multi-section flying wing layouts, and can effectively improve the performance and design efficiency of designed airfoils. Finally, the reliability of this method is verified by an airfoil design process based on the X47-B layout. -
0. 引 言
飞翼布局是无尾布局的一种，因其外形扁平，难以分辨出机身与机翼的分界面，如同一个巨大的机翼，故被称为飞翼布局。此外，飞翼布局又称为全翼布局、翼身融合（Blended Wing Body，BWB）布局。由于飞翼布局具有更高的气动效率，是满足超长航时、超高空、低可探测性等要求的一种布局。它没有传统布局飞机的桶状机身，装载区完全浸没在巨大的机翼内，因此其外形可依气动性能最优的条件进行设计，整个机体都成为一个升力面；同时去除了平尾、垂尾等外形突起部件，有效降低了浸润面积，有助于减少阻力，提高升阻比。由于飞翼布局没有明显的横航向操纵面—垂直尾翼，同时在具有相同装载容积的情况下，机身机翼高度融合，使其外形的全向雷达散射截面（Radar Cross Section，RCS）有很大程度的降低，雷达隐身效果较常规飞机更为出色。因此，飞翼布局飞机在气动效率和隐身性能上相对于传统布局飞机有着无可比拟的优势。
在早期的研究中，由于空气动力学和飞机设计理论发展的滞后与不成熟，飞翼布局的外形暴露出了其先天不足的特性—操纵性与稳定性较常规布局飞机相差很大。飞翼布局飞机因稳定性不足，操纵难度大，飞行控制系统的设计过不了关，而导致设计者们不得不暂时放弃该类布局。直到20世纪60到70年代，随着电子技术的飞速发展，计算机控制技术得到了广泛的应用，使飞机控制系统有了长足的发展，为飞翼布局的重新发展扫清了障碍。20世纪90年代，B-2隐身轰炸机（图1）的成功研制[1-2]，使得飞翼布局再次成为研究热点。B-2的成功充分体现出了飞翼布局的优势，优良的气动性能使其载弹量与B-52相当，且拥有12000 km的空中不加油超远航程，先进的飞翼气动布局形式使其雷达反射面积急剧减小，大约只有同类大小飞机的1%。从此，各国机构纷纷开展了飞翼布局的实用性研究，从目前的研究方向来看，除轰炸机之外，飞翼布局主要应用集中在两个方面—运输机和无人机。
20世纪90年代，波音公司提出了450座级的飞翼运输机方案—BWB-450飞翼运输机（图2），且在2004年与NASA合作设计了X-48系列的飞翼验证机（图3），以进行飞翼布局稳定性和操纵性研究[2-3]；同期欧盟也持续开展了多个飞翼布局运输机项目，包括MOB、VELA等[4-7]，2003年，英国剑桥大学联合美国麻省理工等团队，进行了静音客机项目（SAX）的研究，其中典型代表就是SAX-40[8-18]，如图4所示；俄罗斯重要空气研究中心（TsAGI）也提出了一种兼具飞翼气动效率和常规客机机身结构优势的750座级的混合型飞翼客机方案[19]；在国内，西北工业大学、北京航空航天大学、南京航空航天大学等也持续开展了飞翼客机的总体方案设计研究[20-24]。
目前，无人侦查机、攻击机是一个新的发展潮流。美国已完成了多款飞翼布局无人攻击机的研制，如X-47B（图5）[25]、X-45C[26-27]、RQ180等。同时我国也成功试飞了“利剑”无人机。此外，俄罗斯的“电鳐”、法国主导的“神经元”、英国的“雷神”等无一例外地采取了飞翼布局。可见，飞翼布局无人机是未来无人机发展的一个重要方向。
当然无尾飞翼布局也存在着一些不足：1）飞翼布局存在先天性的纵向和航向的稳定性不足，操纵面设置复杂。同时其纵向尺度相对较短，使得提高纵向操作面效能困难较大，需要依赖多个操纵面和推力矢量等共同产生飞翼布局所需要的各种力和力矩，造成飞控系统操纵律设计困难。2）大型飞翼布局的巡航升阻特性不理想。由于飞翼布局的装载需求几乎完全依赖内翼区域，导致该区域的剖面厚度相对较大，限制了飞翼布局巡航速度的提高。当飞翼布局巡航速度超过其临界马赫数时，全机的激波阻力会显著提高，造成升阻特性损失严重。因此，提高飞翼布局飞机的临界马赫数尤为重要。
飞翼翼型是提升飞翼布局性能的关键手段之一，为此关于飞翼布局翼型的研究层出不穷。根据设计模型的不同可将其分成三类：经典翼型设计、三维布局环境翼型剖面设计及二维/三维翼型综合设计。
1）经典翼型设计。经典翼型是以机翼展向剖面为基础的二维问题。为此翼型设计首先需要以设计机翼飞行状态为基础，应用经验公式将三维设计状态映射为二维设计状态进行设计。Liebeck等[3]通过给出亚声速翼型的理想速度分布，然后进行了BWB-450内翼段翼型设计，得到了后缘反弯的LW109A的翼型；张彬乾等[28]进行了飞翼布局内翼段、外翼段翼型气动、隐身多学科设计，并分析了气动与隐身特性的关系；李权等[29]进行了飞翼布局超临界翼型的设计研究；黄江涛等[30]利用PCA目标降维方法进行了飞翼翼型多学科优化设计。经典翼型优化设计可以快速得到具有良好特性的翼型，但由于设计过程中并未考虑展向横流效应，设计结果在三维布局上难以得到理想的效果。此外，由于需要考虑气动、隐身和控制的多学科翼型设计对设计空间，包括维度和尺度均提出了更高的要求，大大增加了翼型设计难度，同时也降低了翼型设计结果对机翼性能的提升效果。
2）三维布局环境翼型剖面设计。即直接在三维布局上进行翼型剖面优化设计。Pambagjo等[31]以NASA超临界翼型为基础，采用基于小扰动速势方程的余量修正法进行飞翼布局内翼段不同站位翼型剖面设计，设计翼型具有典型的超临界特征；Peigin等[32]以MOB项目的布局为基础，利用基于代理模型全局优化方法，开展了三维环境下翼型剖面外形的单点和多点设计；Hileman等[33]结合内翼段和外翼段翼型的设计要求，利用MSES软件开展了静音客机翼型的反设计；李沛峰等[34]采用直接曲率法（direct iterative surface curvature, DISC），在大型飞翼布局客机上进行外翼段翼型剖面外形设计，以削弱外翼段的激波阻力；Kuntawala等[35]利用基于样条曲线的FFD方法及伴随梯度方法，在飞翼布局上进行了翼型多剖面的气动设计；Zingg等[36]利用梯度算法进行了飞翼布局剖面外形和扭转角设计研究；周琳等[37]利用伴随方法建立了气动外形与隐身协同优化设计方法，并以类X47-B布局为例，对展向不同剖面翼型进行了气动、隐身协同设计；Kanazaki等[38]基于EGO方法，开展了小展弦比飞翼布局客机的翼型设计；Thomas等[39]对比了宽体型和窄体型飞翼布局客机翼型设计，并对比了二者的气动效率和燃油效率；Martins等[40]开展了考虑气动、配平和操纵性的飞翼布局客机设计，并对三个站位的翼型剖面进行优化设计。在飞翼布局三维环境进行翼型剖面设计，可以更好地依照当地流场条件，针对设计要求获得性能更优的翼型。但其最直接的问题就是三维状态物理模型计算量很大，涉及多学科优化问题，对计算资源的需求尤甚，更难实现在广阔设计空间的全局优化。梯度伴随方法的发展虽然可以大幅提高优化效率，但由于梯度算法先天的局部搜索特点，其设计结果对初始输入模型的性能依赖性较大，无法保证收敛到全局最优解。
3）针对上述翼型设计存在的问题，Qin等[7]采用梯度优化方法，先利用经典翼型设计模型进行翼型设计，并以所得设计结果为初值，再进行飞翼布局三维环境下精细化剖面设计，实现了二维、三维条件结合的翼型设计，在一定程度上弥补了单纯经典翼型设计和三维环境剖面优化存在的问题。
由此可见，飞翼布局翼型设计是结合了气动、隐身、控制等复杂多学科设计的问题。这些设计要求很难同时满足，给优化设计带来巨大的困难，进一步造成了经典翼型设计结果在三维布局上应用效果不理想。因此，本文基于飞翼布局展向气动特性分析，进行展向区域划分，分解翼型设计要求，构建分区经典翼型系列设计模型，并以之为基础，进一步在三维飞翼布局上进行多剖面翼型优化设计，提升机翼性能。
1. 飞翼布局翼型设计
翼型是飞行器的基础，翼型的特性对飞行器的特性有重要影响。常规布局翼型的主要目的是提高飞行器气动性能，而飞翼翼型设计则还需要考虑其对布局操稳的贡献。此外，对于考虑隐身影响的军用飞机而言，翼型对整机隐身特性影响尤为重要，在翼型设计中充分融入隐身影响设计，将对整机的RCS降低起重要作用。因此，飞翼布局翼型需考虑气动、控制、隐身等多学科综合设计要求。
翼身融合的布局特性，造成飞翼翼型设计要求繁多且复杂，而飞翼布局展向不同区域的特性需求不一，因此对翼型的要求亦是迥异。因此，为了实现高效的飞翼翼型设计，本文基于飞翼布局研究和探索，以布局分区为基础，分解和简化多学科翼型设计要求，建立了分区翼型设计模型，并形成飞翼翼型系列。
1.1 飞翼布局展向气动特性分析
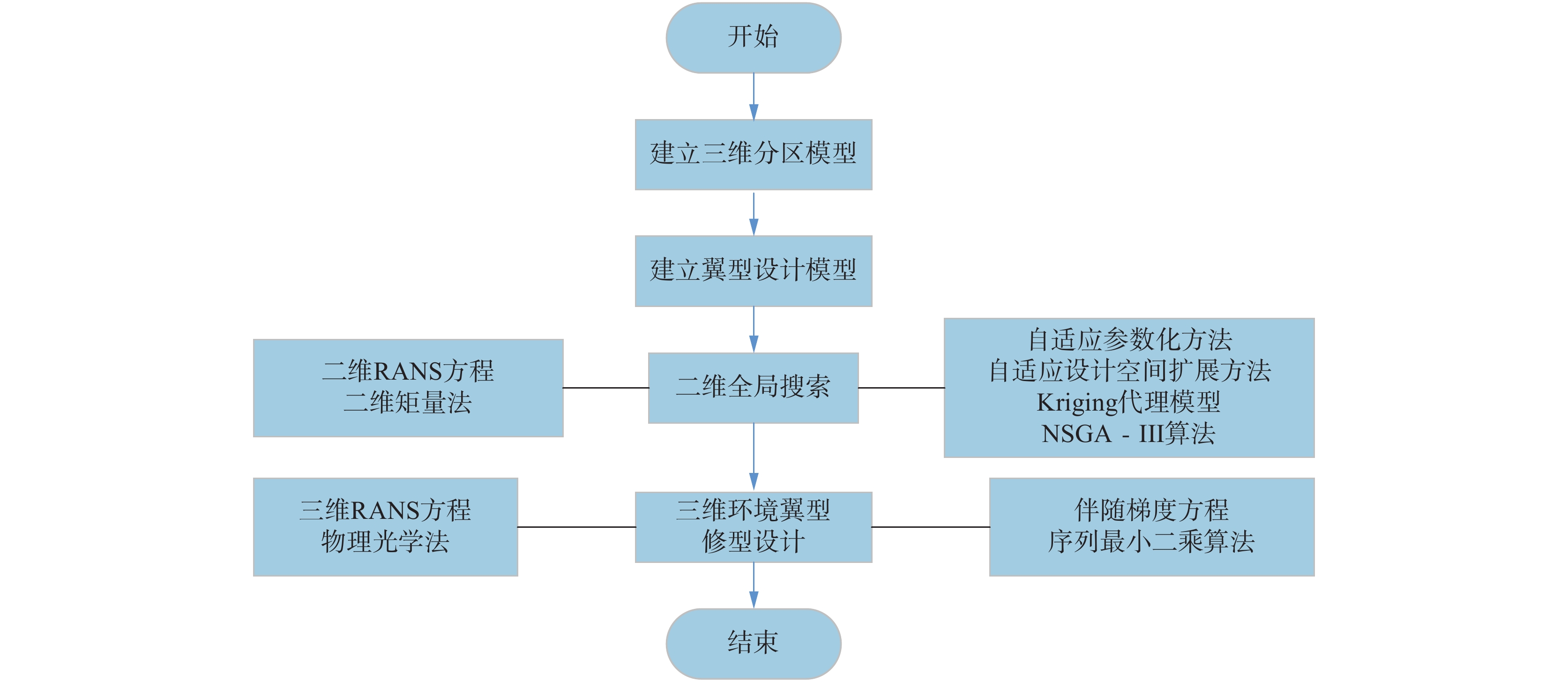
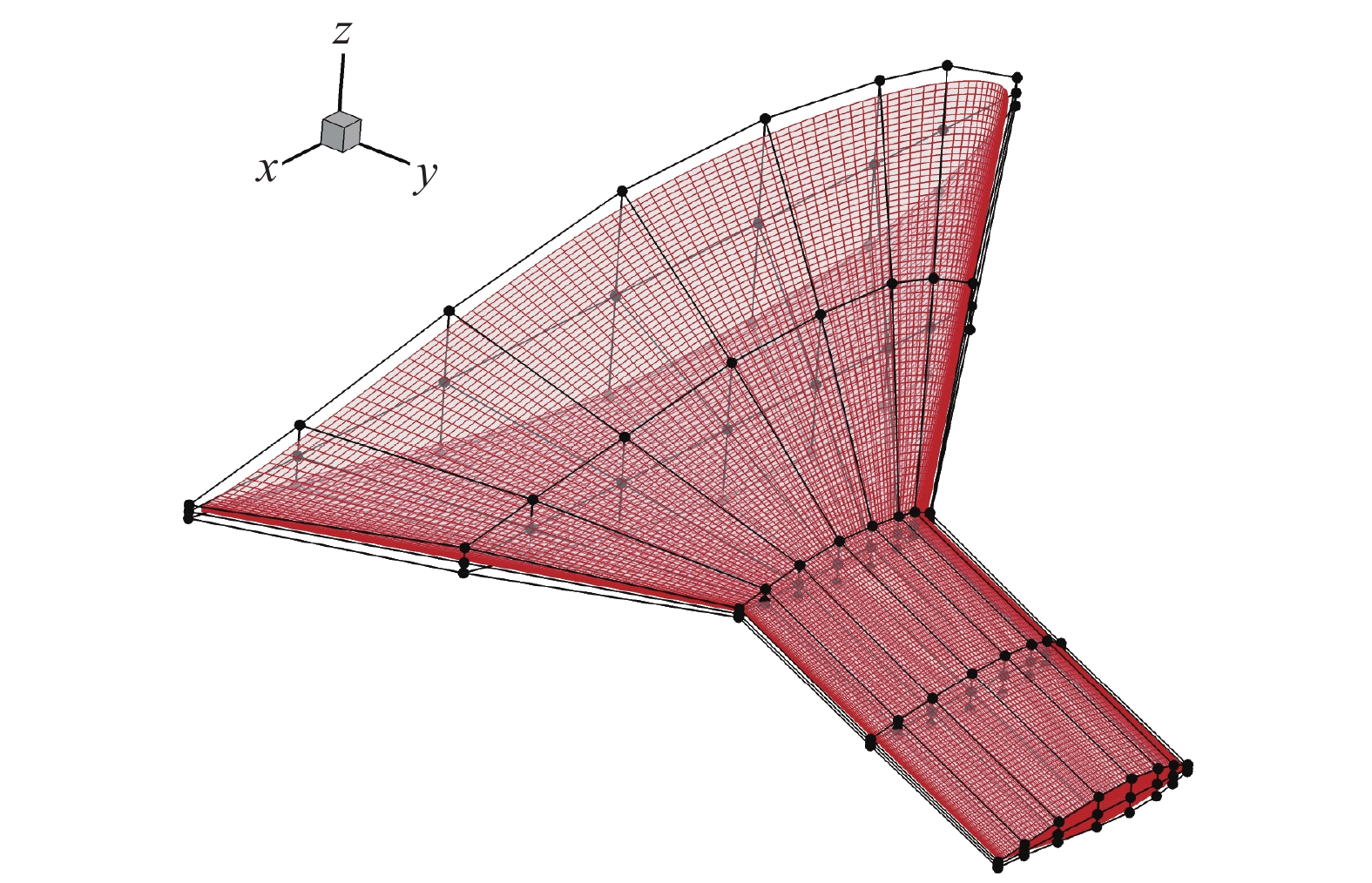
为了分析飞翼布局展向气动分布特点，本文选取典型双后掠飞翼布局（图6）为例。该布局外形类似X-47B飞机，内翼段后掠角接近60°，外翼段后掠角接近30°。由于飞翼布局内翼区承担了主要的装载任务，因此其当地厚度和弦长一般远大于外翼段。飞翼布局通常要求在保持纵向力矩配平的同时，具有高巡航升阻比以及良好的巡航效率。因此，本文选取典型跨声速巡航状态（
Ma=0.80,CL=0.30,Re=6.8×106 ）进行流场及气动特性分析。图7展示了类X-47布局压力分布云图，图左侧是上表面压力分布，右侧是下表面压力分布。由图可知，在当前计算状态下，外翼段出现了更加明显的激波。图8和图9分别展示了相应的展向升力系数分布和环量分布。该布局内翼段当地升力系数较小，并沿着展长逐渐提高，在外翼区达到最大，随后逐渐降低。由于本文计算几何模型简化了翼尖区，导致翼尖区当地弦长过长，因此升力系数在翼尖区有个陡升。
由图8可知，飞翼布局内翼段虽然厚度较大，但由于升力系数较小，所以内翼段并未产生明显的激波，而外翼段高升力导致飞翼布局中间区域内侧开始产生强激波，横跨整个外翼区，直至延伸到翼尖区。而当地弦长的差距导致该布局的当地载荷从内翼段到外翼段逐渐降低（如图9所示），呈现近似三角形分布[7]，这种分布形态体现了激波阻力和诱导阻力权衡的结果。
综上所述，对于双后掠飞翼无尾布局而言，中央体区和中间区承担着纵向力矩配平的任务，中间区至翼尖区则是气动减阻的重点关注对象，因此，本文将以双后掠飞翼布局，进行飞翼翼型设计模型和设计方法研究。
1.2 飞翼布局翼型分区设计要求
传统布局飞机，如运输机和无人机等，要求具有良好巡航气动效率和起降性能，因此其翼型一般要求如下：
1）在飞机的整个使用范围内，翼型必须具有高巡航升阻比，良好的阻力发散特性以及较小的压缩性阻力增量等；
2）具有足够的抖振边界，构成的机翼在超过飞机巡航马赫数一定范围内不出现抖振；
3）后加载产生的低头力矩控制在一定范围内，以降低配平阻力和尾翼载荷；
4）具有高的最大升力系数和失速特性，以简化增升装置的设计。
与传统布局飞机相比，飞翼布局飞机对翼型气动设计进一步提出了更加严苛的要求，在传统的气动特性基础上，加强了对力矩特性、边界特性的要求等，具体来说有以下方面的设计要求：
1）纵向自配平的力矩特性，由于尾翼的缺失和操纵面设置复杂等问题，飞翼翼型需要尽可能实现巡航设计点的力矩自配平，以缓解飞机操纵控制方面的压力，降低飞机控制系统的设计难度；
2）更好的阻力发散特性，高跨声速乃至超声速巡航是未来飞机重要发展的趋势，而飞翼布局的装载要求导致其翼型厚度相对较大，因此需要提高翼型的阻力发散特性以满足飞机巡航效率、抖振边界等设计要求；
3）与传统布局飞机不同，飞翼布局融合了机翼机身，因此内翼段机翼承担了装载要求，需要有大的容积和厚度；
4）除气动设计要求外，良好特性的飞翼布局对其翼型还需其他学科要求的协同设计，如隐身、结构等。翼身高度融合的布局的空间外形、部件外形和外载荷分布等与传统布局不同，因此需要进行结构优化设计以满足飞行包线、飞行安全的设计要求等；而隐身特性直接关系到军用飞机的作战能力和战场生存能力，飞翼布局飞机作为天生的低RCS布局，更需要在翼型设计阶段融合RCS影响，以充分发挥布局优势。
以上飞翼布局对翼型设计的整体要求，通常这些要求很难同时满足，而飞翼布局不同区域的性能需求不一，因此各处翼型的学科要求也不尽相同，需要结合三维布局分区的设计要求，提炼不同站位翼型的设计模型，分别进行优化设计。结合上述分析，本文基于经典的双后掠飞翼布局，建立了三维分区翼型设计理念，将布局分解为中央体区、中间区域和外翼区以及翼尖区，构建分区翼型设计模型，以满足整个飞机的设计要求。对于气动隐身特性需求较高的双后掠军用飞翼布局而言，其翼型通常需要满足以下要求：
1） 中央体区，又称内翼区，该区域翼型在满足装载需求的同时，还需要具有良好的升阻特性和隐身特性。此外还需要一定抬头力矩，促进实现布局的纵向力矩配平；
2） 中间区域和外翼区一般是激波集中产生的区域，因此该区域的翼型设计除保障装载需求以外，需要具有良好的巡航升阻特性以及阻力发散特性，且该区域距离重心位置较近，需要尽可能减少低头力矩乃至增加抬头力矩以满足纵向力矩的配平需求；
3）翼尖区的翼型需要降低巡航阻力，提高升阻比，以获得高效的巡航效率，还要具备良好的低速升力特性和失速特性，推迟起降分离，为飞翼布局的起降阶段提供升力。此外，还需要良好的隐身特性。
飞翼布局外翼区和内翼区翼型设计是两种截然不同的思路。气动设计方面，对于外翼段翼型，主要是减小巡航阻力同时提高隐身特性，以保证较高巡航效率和减小起飞着陆的失速速度，因此外翼段翼型大多采用超临界翼型；对于内翼段翼型，主要要求其具有较高的抬头力矩，以中和外翼段产生的低头力矩，实现巡航状态纵向力矩配平。
1.3 飞翼布局翼型的典型特征
以往飞翼翼型设计已经体现了分区的思路，主要是基于翼型力矩配平的设计策略。力矩系数和翼型的弯度线形状息息相关，为了满足纵向力矩配平的要求，BWB-450采用翼型后缘反弯[41]，即后缘反加载的策略设计内翼段翼型，以提供抬头力矩，而外翼段通过合理的翼型选配设计以及扭转分布，保证了配平状态下展向近似椭圆形状的载荷分布，减小了飞机的诱导阻力，使飞翼布局的气动特性优势得到了更加充分的发挥，如图10所示。但后缘反弯剖面的中央体设计，会导致巡航性能的牺牲，且需要更大的控制面和舵机实现飞机控制。
![]()
图 10 BWB-450飞翼布局运输机翼根翼型Figure 10. The entral body of a BWB-450 flying wing transport aircraft针对这一问题，静音客机SAX-29、SAX-40采用了前缘下表面前弯的外形[33]。绕此类外形气动压心前移，因此这种翼型组成的中央体外形可实现无平尾的纵向平衡，且没有由尾翼平衡引起的升力损失。在巡航过程中燃油消耗引起的重心变化用增大矢量推力角来平衡，使静安定裕度保持为6％～9.5％，而采用后缘反弯的BWB布局，该裕度只能达到5％。图11展示了静音客机系列的翼型配置和压力分布，从中可以看出，内翼段采用了前加载翼型，当地升力系数较小，且主要集中于前缘部分，提供了抬头力矩，后缘升力系数基本为0。外翼段采用了典型的超临界翼型，当地升力系数较高，上表面存在弱激波，压力恢复较为和缓，且具有明显的后加载特征。此外，前加载翼型能够对气动特性和隐身特性进行合理折中，是一种理想的飞翼布局中央体翼型。如美国研制的B-2隐身轰炸机（图12）采用的就是前加载翼型。
综上所述，由于飞翼布局不同区域对翼型的设计需求不同，导致当地翼型的外形特征和压力分布不尽相同，因此飞翼翼型设计不可一概而论，应当结合不同区域的需求，建立分区设计模型，实现高效、便捷的翼型设计。
2. 飞翼布局翼型设计方法
2.1 传统修型设计
早期的飞翼翼型设计主要依赖设计者的工程经验，结合设计对象的特性要求，对现有翼型外形进行修型。如波音公司的Liebeck通过给出翼型理想速度分布进行反弯翼型的修型设计[3]。
2.2 反设计
翼型反设计思想的提出可追溯到20世纪30年代NACA6系列翼型的设计。Jacobs提出翼型流场分析理论可逆向应用于翼型设计，即根据目标气动特性求解翼型几何[42-44]。常用的反设计方法包括余量修正法（Iterative Residual-correction Method）[15]、表面曲率法（Direct Iterative Surface Curvature，DISC）[16]、表面流线法（Constrained Direct Iterative Surface Curvature，CDISC）[20]以及Gappy POD方法[21]等。这些方法在飞翼翼型设计中得到广泛应用，虽然反设计方法效率很高，但需要预先给定压力分布，这一点依赖于设计人员的经验，而对于新的设计构型，压力分布很难给出，也不能保证存在对应的几何外形。其次，即使存在对应外形，也不能保证所给的目标流动分布就是最优的，这在很大程度上影响了设计的效果，反设计方法很难兼顾低速等其他设计要求[45]。
2.3 基于数值优化设计方法
基于数值优化的设计方法，主要设计思路是采用基于物理计算模型和现代数值优化算法结合的气动力设计方法对飞行器外形进行优化，其由参数化方法、优化算法以及物理计算模型构成。而根据优化算法的不同可将其分为两类：1）基于进化类算法的全局优化设计[46-47]；2）基于梯度算法的局部优化设计[48]。对于精细化优化设计问题，物理计算模型需要较大的内存和CPU资源，且进化类算法对物理计算模型的调用次数过多，复杂问题对计算资源的需求往往大到难以接受的地步，因此设计者们基于取样方法和代理模型技术，发展了基于代理模型的全局优化设计方法。优化设计方法也是应用最广泛的飞翼翼型设计方法。
飞翼布局翼型设计是结合了气动、隐身和控制的复杂多学科设计问题。复杂的设计要求导致其与传统翼型设计迥异，需要在广阔的设计空间内进行全局优化，这对基于代理模型的优化设计造成了困难。针对代理模型优化的设计空间构造问题，本文采用了课题组开发的Bspline曲线的自适应方法[49]。该方法选择敏感区域加入新的变量，实现设计空间维度扩展，利用Bspline曲线的节点插入算法，对样本进行精确地高维重构。同时利用自适应设计空间扩展方法[50]对表现较好的有效样本的设计变量边界进行检测，进行尺度扩展，有效提高了样本的利用率，确保优化在充足的设计空间内高效地进行。结合分区翼型设计模型共同组成了二维翼型设计方法。
针对经典翼型设计结果对飞翼布局性能提升不理想的问题，本文建立了三维环境下翼型修型设计。由于三维流动环境下翼型设计的设计变量数和计算代价较大，基于代理模型的全局优化方法在面临高维设计变量时会面临“维度灾难”问题，因此课题组发展了基于样条曲线的FFD（Free Form Deformation，FFD）方法以及梯度伴随的序列最小二乘算法（Sequential Least Programming，SLSQP）[51]的梯度优化设计方法，实现高效的三维环境翼型修型设计。FFD方法适用于任意网格形式和拓扑结构，可以简单、直接且高效地控制物体的变形，因此在飞行器三维气动外形优化设计中应用十分广泛。序列最小二乘算法是一种适用于非线性约束的梯度优化算法，可以处理等式和不等式约束。该算法可以逐次逼近目标函数的二阶近似方程和约束的一阶近似方程，能够有效处理拥有大规模设计变量的非线性多约束问题。
2.4 气动隐身多学科设计
为了充分发挥飞翼布局的气动隐身特性，需要对飞翼翼型进行多学科设计。气动隐身多学科设计包括气动、隐身计算模型以及设计方法。高效高精度的物理计算模型是优化设计的基础。在气动计算中，本文二维翼型/三维布局均采用高精度的基于雷诺平均Navier-Stokes（RANS）方程，实现高效的流场模拟。无黏项采用迎风格式，黏性项采用中心离散格式，采用近似因式分解法进行时间推进求解，湍流模型一律采用SST两方程模型。在隐身计算中，过去大多是将二维翼型沿展向拉成三维机翼，利用高频近似物理光学法（Physical Optics，PO）及其混合方法进行RCS计算，计算效率低。因此本文在二维翼型设计中，采用高效的二维矩量法[52]进行翼型隐身特性的计算。该方法是麦克斯韦方程的精确求解方法。文献[49]验证了二维矩量法的精度和可靠性。在三维布局优化设计中，采用物理光学法进行三维RCS特性求解。
气动、隐身多学科设计是典型的多目标问题。对于多目标问题，优化解表现为一个解集，即Pareto前沿。设计人员根据Pareto前沿的分布进行多目标决策，获得最终的优化解。多目标遗传算法是求解多目标优化问题Pareto前沿的最有效方法之一。遗传算法（GA）借鉴生物进化的思想，通过计算机模拟物种繁衍父代遗传基因的重新组合与“优胜劣汰”自然选择机制的联合作用，解决科学与工程中的复杂问题。本文采用NSGA-Ⅲ（Non-dominated Sorting GeneticAlgorithm Ⅲ）[53]方法进行翼型多学科优化设计。
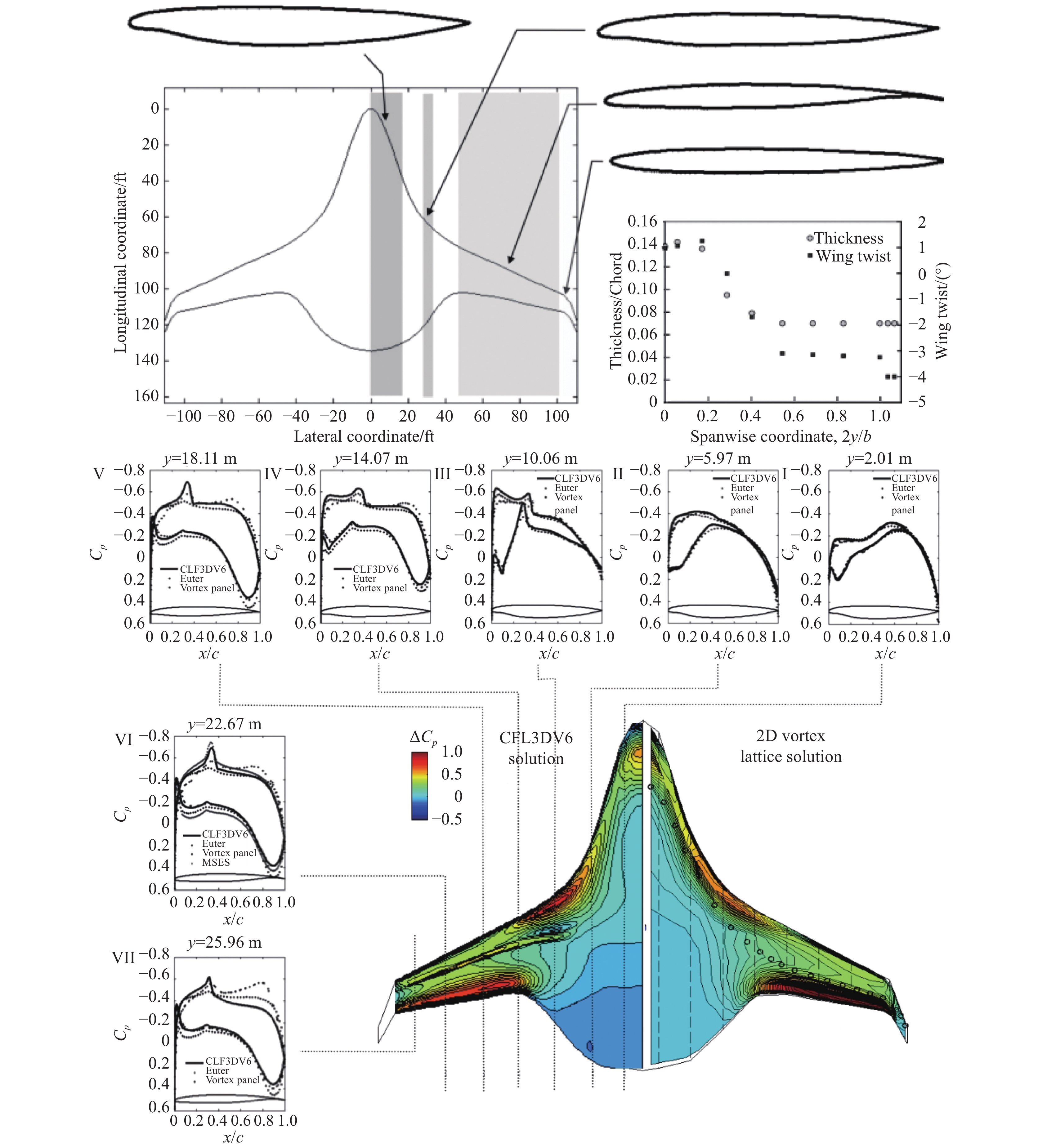
2.5 翼型优化设计框架
基于三维分区设计理念，构建了不同站位的二维设计模型，结合自适应参数化方法、自适应设计空间扩展方法、Kriging代理模型和NSGA-III算法，建立了二维翼型设计方法。并针对三维效应下二维设计结果难以充分发挥作用的问题，结合FFD方法和序列最小二乘法建立三维环境翼型修型设计方法。结合气动、隐身计算模型，建立了“全局+局部”的飞翼翼型多学科优化设计方法。优化流程如图13所示。
![]()
图 13 “全局+局部”飞翼翼型多学科优化设计方法流程图Figure 13. Flow chart of the global/local multidisciplinary optimization method for designing flying-wing airfoils3. 飞翼布局翼型设计方法
3.1 气动隐身多学科设计
根据飞翼布局飞机翼型设计要求，以NACA 65016翼型[37]为基础翼型进行优化设计，设计状态为
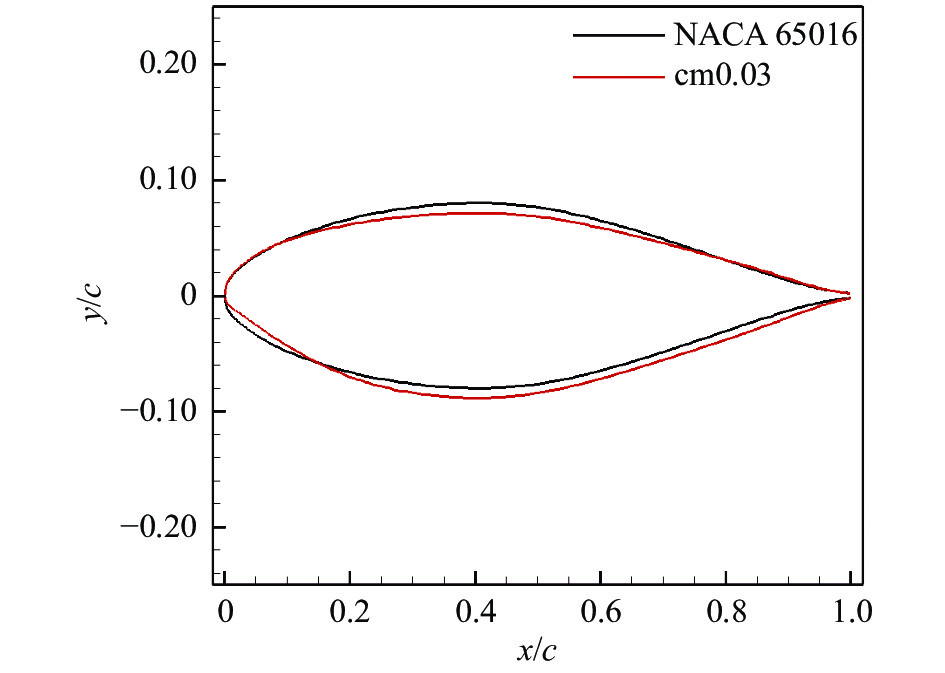
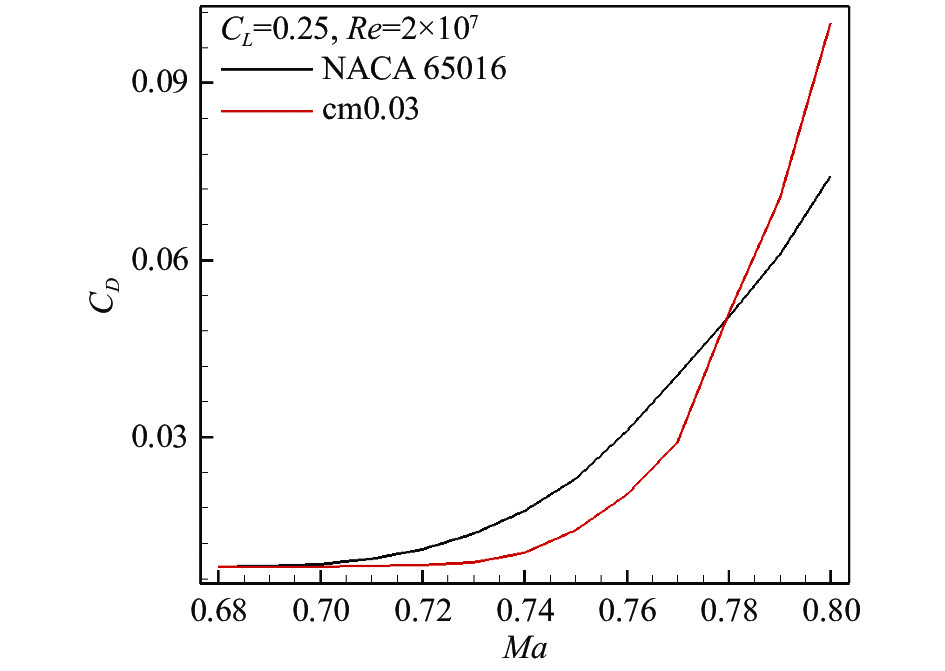
Ma= 0.70、CL=0.25、Re=20×106 。翼型设计模型如下：min (1) 图14和图15为设计翼型外形和压力分布对比，从中可以看出，比起初始翼型NACA 65016，设计翼型cm0.03前缘半径减小，后缘负弯度增加，具有明显的前缘正加载和后缘反加载特征，上表面外形趋于平坦，最大厚度位置后移。设计状态下初始翼型的强激波被削弱为两道弱激波，有利于提高阻力发散特性，如图16所示，阻力发散马赫数提高至0.74，同时翼型力矩特性明显提升，如图17所示。
为了验证设计翼型的优化效果，将设计翼型的装配到类X47-B三维布局[37]。X47-B是典型的小展弦比无人机布局，要求有高效的巡航效率和隐身特性。本节首先研究设计翼型对其气动特性的改善。该布局几何外形和基本参数分别如图18和表1所示。其中，设计翼型cm0.03装配到内翼段，利用Xfoil改变设计翼型的相对厚度为13%和11%，其中13%厚度的cm0.03_13装配到中间区域，11%厚度的cm0.03_11装配到翼尖区域，形成设计方案OptModel_1，然后与对称翼型配置的布局方案BaseModel进行计算对比。计算状态如表2所示。
表 1 基准布局几何参数Table 1. Geometric parameters of the base model参数 值 展长 /m 18.93 参考面积 /m2 87.42 重心位置 /m (6.17,0,0) 平均气动弦长 /m 6.57 表 2 气动计算状态Table 2. Conditions for aerodynamic computation参数 设置 巡航马赫数 0.8 升力系数 0.3 单位尺度雷诺数 6.8×106 图19为计算结果和压力分布云图对比，相较于BaseModel，OptModel_1阻力系数降低41.9 counts （1 counts = 0.0001），力矩系数提高了0.013。内翼段激波基本消除，外翼段前缘低压区向前扩张，后缘压力线分布更加均匀，压力恢复和缓。虽然由于布局参数和重心位置等原因，OptModel_1还未达到完全配平，但OptModel_1低头力矩有很明显的减弱，纵向力矩配平明显改善。但OptModel_1外翼段仍旧有明显的激波，且前缘低压区较小，升阻特性没有充分达到优化设计的效果，还有很大的改进余地。
综上，对飞翼布局翼型设计而言，不同区域的翼型设计不可一概而言，应当结合当地区域的设计要求，进行分区翼型设计。
3.2 分区翼型系列设计
根据上述讨论，建立分区翼型设计模型，并形成基于区域划分的翼型系列。
中央体区翼型设计状态为
Ma = 0.65、\;{C_L} = 0.25 。气动特性要求在保持抬头力矩同时提高升阻特性。\begin{split} \min :&{C_D}\;\; \\ {\rm{s.t.}}:& {C_L} = 0.25 \\& {C_m} \geqslant 0.05 \\& t/c \geqslant t/{c_{{\rm{initial}}}} \end{split} (2) 中间区翼型设计状态为典型跨声速设计状态
Ma = 0.73、{C_L} = 0.55 。基准翼型为相对厚度13%的对称翼型NACA 65013。Kink 站位翼型气动设计要求在保持抬头力矩同时提高升阻特性和阻力发散特性，设计模型如式（3）所示。\begin{split} \min :& {C_D}\;\; \\ {\rm{s.t.}}:& {C_L} = 0.55 \\& {C_m} \geqslant 0.01 \\& {C_{D\_0.75}} - {C_{D\_0.73}} \leqslant 0.001 \\& t/c \geqslant t/{c_{{\rm{initial}}}} \end{split} (3) 翼尖区翼型的设计要求为减阻和提升阻力发散特性，约束为设计翼型的力矩系数不小于初始翼型，同时保持最大厚度不减小。设计状态为
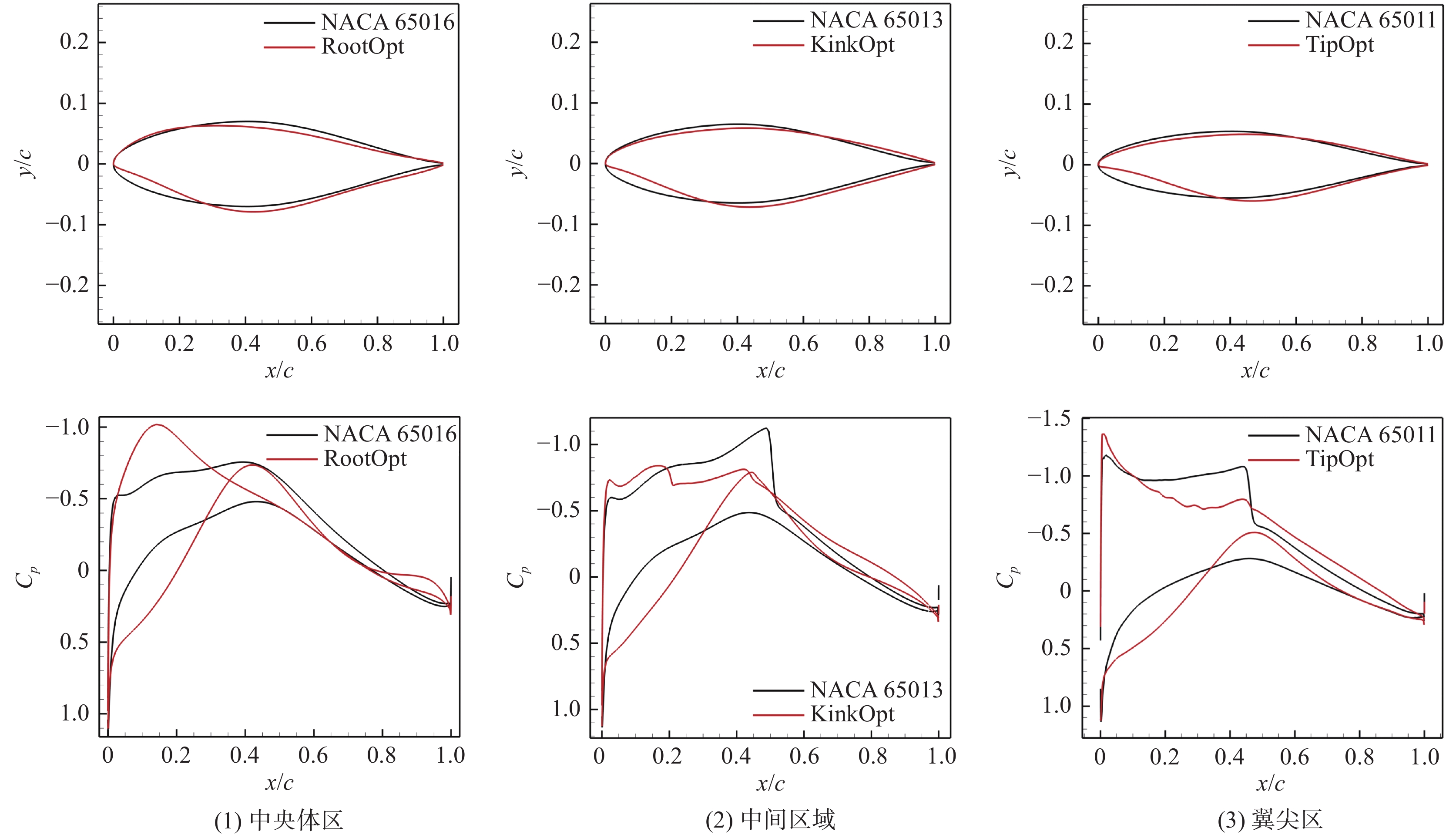
Ma = 0.73、 {C_L} = 0.35 。隐身设计要求与之前保持一致。基准翼型为NACA 65011。设计模型如式（4）所示。\begin{split} \min :& {C_D}\;\; \\ {\rm{s.t.}}:& {C_L} = 0.35 \\& {C_m} \geqslant {C_{m\_{\text{initial}}}} \\& {C_{D\_0.75}} - {C_{D\_0.73}} \leqslant 0.001 \\& t/c \geqslant t/{c_{{\text{initial}}}} \end{split} (4) 表3为设计翼型的计算结果对比。相较于各初始翼型，设计翼型阻力特性均有明显的改善，力矩系数满足约束。图20为不同区域设计翼型外形和压力分布对比。可以看出，设计翼型前缘半径减小，呈现明显的前加载特征。由于抬头力矩约束，内翼段和中间区域翼型后缘均出现不同程度反加载特征。翼尖区域翼型呈现典型跨声速压力分布特征，跨声速设计状态的翼型最大厚度位置前移。在亚声速低载荷状态下，内翼段翼型设计前后的流场并未出现明显的激波。由于不同设计升力系数，中间区域设计翼型和翼尖区域翼型呈现了不同的跨声速特征。
表 3 设计翼型计算结果对比Table 3. Comparison of computational resultsConfiguration CL CD Cm α NACA 65016 0.250 0.0067 0.0058 1.51° RootOpt 0.250 0.0065 0.0503 2.45° NACA 65013 0.550 0.0079 –0.0113 1.74° KinkOpt 0.550 0.0067 0.0105 2.08° NACA 65011 0.350 0.0077 –0.0072 2.80° TipOpt 0.350 0.0069 0.000 2.92° ![]()
图 20 不同区域设计翼型外形和压力分布对比Figure 20. Comparison of airfoil shapes and pressure distribution on different partitions从图21可以看出，装配分区设计翼型的布局阻力降低了79.3 counts，力矩系数提高0.02，改善明显。内翼段激波基本完全消除，外翼段前缘低压区扩张，后缘压力线分布更加均匀，压力恢复和缓。但对飞翼布局而言，机翼横向流动效应明显，对此在翼型设计模型中并未加以考虑，因此未能充分发挥翼型设计的优势，布局的激波依旧比较明显。鉴于此，本文提出了三维环境的翼型修型设计方法，进一步提升翼型性能。
3.3 三维环境多剖面翼型设计
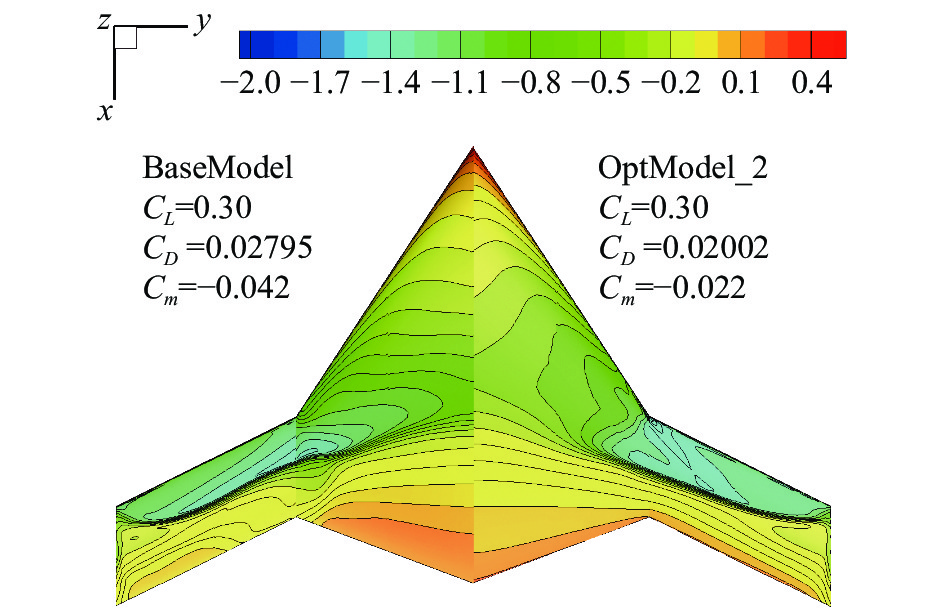
通过二维翼型全局设计，三维布局的气动特性明显提升.为了进一步提升设计翼型性能。使之充分发挥设计效果，在二维设计完成后，利用基于气动伴随方程的梯度方法，进行三维环境翼型修型设计，即优化的初始外形为OptModel_2。设计目标为巡航状态下减阻和提高RCS特性，同时保持三个站位处翼型最大厚度不减小以及保持低头力矩不增加。计算模型如式（5）所示。
\begin{split} \min :&{C_D}\; \\ {\rm{s.t.}}:& {C_L} = 0.3 \\& {C_m} \geqslant {C_m}_{{\text{,ori}}} \\& {t_n} \geqslant {t_{n\_{\text{low}}}}{,^{}}n = 1,2,3 \end{split} (5) 最终优化结果为OptModel_3。从图22可以看出，相较于OptModel_2，OptModel_3阻力系数减小35 counts，力矩系数保持不变，并且外翼段的激波明显减弱，翼尖区的激波被基本消除。图23为各站位翼型剖面和压力分布对比，红色为三维修型翼型和压力分布，黑色为初始翼型和压力分布。从图23中可以看出，内翼段的修型翼型没有明显变化；中间区的修型翼型前缘半径减小，中部正弯度增加，后缘负弯度增加；翼尖区的修型翼型前缘正弯度和后缘负弯度明显增加。
![]()
图 23 三维优化设计翼型和压力分布对比Figure 23. Comparison of airfoil shapes and pressure distributions obtained by 3D optimization design由上文可知，后缘反加载的翼型特征对气动特性有不利影响，而前缘正加载翼型可以很好地协调翼型的气动特性。在二维翼型设计中，各站位设计翼型均呈现明显的前缘正加载和后缘反加载，共同配合以满足气动特性设计需求。而三维修型设计对二维设计结果的外形进行了微调，尤其是前缘正加载和后缘反加载的分布，即翼型弯度分布。通过调整翼型各剖面的弯度分布，改善了布局的载荷分布，使其气动特性得到进一步提升。
3.4 气动隐身多学科设计
由上文可知，军用飞机翼型除了良好的巡航升阻特性和纵向力矩配平特性以外，还需要良好的隐身特性。因此，本节利用多目标遗传算法进行各区翼型气动隐身设计。在此过程中，各区翼型气动设计要求不变，隐身特性要求在入射频率9 GHz下，前向
\pm 30 °均值降低。入射角示意图如图24所示。为了在不损失布局气动特性的基础上，进一步提升飞翼布局外翼段的RCS特性，翼尖区设计两组翼型，分别为气动特性占优的翼型和隐身特性占优的翼型。气动特性占优的翼型装配于三维布局的外翼段距离翼尖1/4处位置，隐身特性占优的翼型位于外翼段翼尖处。 表4为三维布局隐身计算状态。
表 4 隐身计算状态Table 4. Conditions for the stealth computation参数 设置 入射频率 9 GHZ 极化方式 垂直极化 随后利用气动隐身伴随方法进行进一步的三维环境翼型修型设计，设计目标为减阻和提高RCS特性，保持低头力矩系数不增加及各剖面翼型厚度不降低。设计模型如式（6）所示。
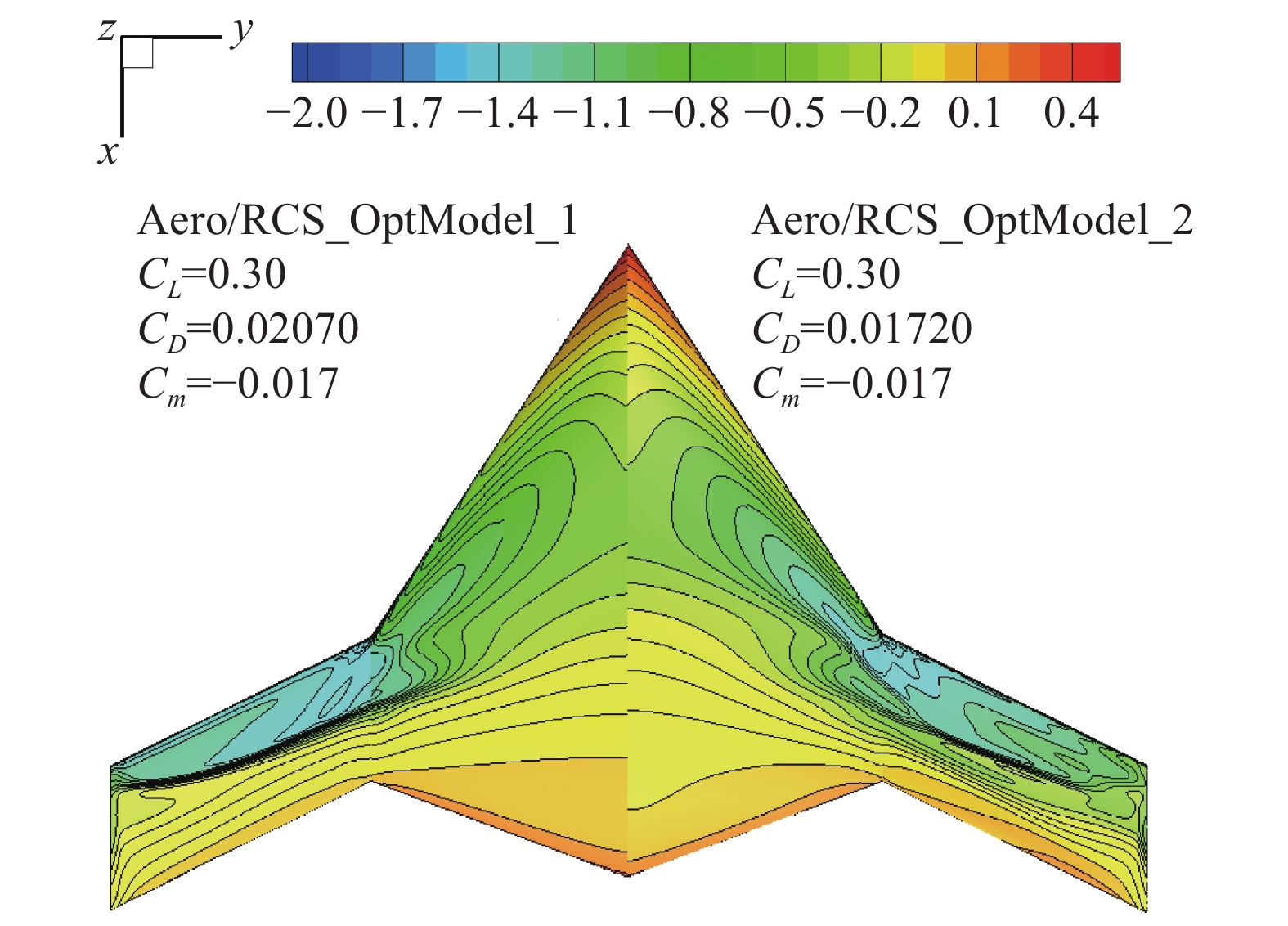
\begin{split} \min :& {C_D}\;\;{\rm{RCS}} \\ {\rm{s.t.}}:& {C_L} = 0.3 \\& {C_m} \geqslant {C_m}_{{\text{,ori}}} \\& {t_n} \geqslant {t_{n\_{\text{low}}}}{,^{}}\;n = 1,2,3 \end{split} (6) 图25～图28为Aero/RCS_OptModel_Ⅰ与设计结果Aero/RCS_OptModel_Ⅱ气动隐身特性计算对比。Aero/RCS_OptModel_Ⅱ阻力系数降低35 counts，力矩特性保持。从压力分布云图对比可以看出，Aero/RCS_OptModel_Ⅱ中央体区、中间区域和翼尖区的激波基本消除，但外翼段中部还有较为明显的激波。在各区域设计翼型对比中，翼尖处翼型的外形改变较为明显，翼型前缘正弯度和后缘负弯度有明显的增加，其余剖面翼型外形变化不大。表5为前向RCS均值对比，可以看出 Aero/RCS_OptModel_Ⅱ的隐身特性与Aero/RCS_OptModel_Ⅰ基本持平，改善不大。
![]()
图 26 三维优化设计翼型和压力分布对比Figure 26. Comparisons of airfoil shapes and pressure distributions obtained by 3D optimization design综上所述，在分区系列设计中，翼型气动隐身设计对三维飞翼布局的气动隐身特性有明显的改善。但由于二维翼型模型无法考虑横向流动效应，导致设计翼型装配到三维布局上无法充分发挥设计效果。三维环境的翼型修型设计可以进一步提升布局的气动特性。对于隐身特性而言，翼型分区设计效果显著，而三维环境的修型设计对隐身特性的改善不明显。
表 5 前向RCS均值（单位：m2）Table 5. Average frontal RCS (unit: m2)Configuration 偏航
(–60° ～ 60°)俯仰
(–30° ～ 30°)BaseModel 1.0903 0.1609 Aero/RCS_OptModel_Ⅰ 0.3020 0.0036 Aero/RCS_OptModel_Ⅱ 0.3015 0.0031 4. 结论与展望
为了充分发挥飞翼布局飞机气动、隐身特性的布局优势，需要对其翼型进行高效设计。本文针对飞翼布局翼型的气动、隐身设计问题，提出了一种“全局+局部”的翼型多学科优化设计方法，以类X47-B布局为例，进行了内翼区、中间区和翼尖区的翼型优化设计，得到结论如下：
1） 飞翼布局各区翼型设计要求不尽相同。内翼区翼型需要抬头力矩以帮助布局达到纵向力矩配平，以及良好的隐身特性，中间区翼型要求具有良好的巡航升阻特性、阻力发散特性和一定的抬头力矩以配合实现纵向力矩配平，而翼尖区则面临气动减阻和隐身特性的设计要求。
2） 由于抬头力矩约束和隐身设计要求，飞翼布局翼型均呈现明显的前缘正加载和后缘反加载的外形特征。翼型两种加载特征的合理配置，可以在保持纵向力矩配平的同时，实现飞翼布局气动、隐身特性的共赢。
3） 基于飞翼布局各区翼型设计要求，建立了分区翼型设计模型，利用基于代理模型的全局优化方法进行优化设计，并形成了分区翼型系列。为了进一步提高翼型特性，在分区翼型系列的基础上，利用梯度伴随方法进一步进行三维环境翼型修型设计。建立的“全局+局部”的翼型多学科优化设计方法，可以提高优化设计效率，使设计结果更加满足工程实际的设计要求。
4） 飞翼翼型因飞翼布局飞机的种类、需求导致其设计要求不可一概而论。本文主要针对飞翼布局无人军用机进行了翼型系列的设计，未来将在此基础上，开展考虑起降特性的大展弦比的飞翼运输机、考虑层流设计的高空长航时飞翼无人机等翼型。由于飞翼布局的三维流动效应很强，因此拟结合风洞试验，对设计翼型系列的气动性能进行验证，为飞翼翼型的选配提供进一步支撑。
-
![]()
图 10 BWB-450飞翼布局运输机翼根翼型
Figure 10. The entral body of a BWB-450 flying wing transport aircraft
![]()
图 13 “全局+局部”飞翼翼型多学科优化设计方法流程图
Figure 13. Flow chart of the global/local multidisciplinary optimization method for designing flying-wing airfoils
![]()
图 20 不同区域设计翼型外形和压力分布对比
Figure 20. Comparison of airfoil shapes and pressure distribution on different partitions
![]()
图 23 三维优化设计翼型和压力分布对比
Figure 23. Comparison of airfoil shapes and pressure distributions obtained by 3D optimization design
![]()
图 26 三维优化设计翼型和压力分布对比
Figure 26. Comparisons of airfoil shapes and pressure distributions obtained by 3D optimization design
表 1 基准布局几何参数
Table 1 Geometric parameters of the base model
参数 值 展长 /m 18.93 参考面积 /m2 87.42 重心位置 /m (6.17,0,0) 平均气动弦长 /m 6.57 
下载: 导出CSV
表 2 气动计算状态
Table 2 Conditions for aerodynamic computation
参数 设置 巡航马赫数 0.8 升力系数 0.3 单位尺度雷诺数 6.8×106
下载: 导出CSV
表 3 设计翼型计算结果对比
Table 3 Comparison of computational results
Configuration CL CD Cm α NACA 65016 0.250 0.0067 0.0058 1.51° RootOpt 0.250 0.0065 0.0503 2.45° NACA 65013 0.550 0.0079 –0.0113 1.74° KinkOpt 0.550 0.0067 0.0105 2.08° NACA 65011 0.350 0.0077 –0.0072 2.80° TipOpt 0.350 0.0069 0.000 2.92°
下载: 导出CSV
表 5 前向RCS均值（单位：m2）
Table 5 Average frontal RCS (unit: m2)
Configuration 偏航
(–60° ～ 60°)俯仰
(–30° ～ 30°)BaseModel 1.0903 0.1609 Aero/RCS_OptModel_Ⅰ 0.3020 0.0036 Aero/RCS_OptModel_Ⅱ 0.3015 0.0031
下载: 导出CSV
-
[1] 卢成文, 主编. 世界飞机手册[M]. 北京: 航空工业出版社, 1994. [2] GRIFFIN J M, KINNU J K, COLOMBI J M. B-2 systems engineering case study[R]. Defense Technical Information Center, 2007. ADA 464771. doi: 10.21236/ada464771
[3] LIEBECK R, PAGE M, RAWDON B. Blended-wing-body subsonic commercial transport[C]//36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. Reston, Virigina: AIAA, 1998. AIAA-98-0438. doi: 10.2514/6.1998-438
[4] MORRIS A, MOB A. European distributed multi-disciplinary design and optimisation project[C]//9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, Georgia. Reston, Virginia: AIAA, 2002. AIAA 2002-5444. doi: 10.2514/6.2002-5444
[5] LABAN M, ARENDSEN P, ROUWHORST W, et al. A computational design engine for multi-disciplinary optimisation with application to a blended wing body configuration[C]//9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, Georgia. Reston, Virginia: AIAA, 2002. AIAA 2002-5446. doi: 10.2514/6.2002-5446
[6] LA ROCCA G, KRAKERS L, VAN TOOREN M. Development of an ICAD generative model for blended wing-body aircraft design[C]//9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, Georgia. Reston, Virginia: AIAA, 2002. AIAA 2002-5447. doi: 10.2514/6.2002-5447
[7] QIN N. Aerodynamic studies for blended wing body aircraft[C]//9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, Georgia. Reston, Virigina: AIAA, 2002. AIAA 2002-5448. doi: 10.2514/6.2002-5448
[8] HILEMAN J, SPAKOVSZKY Z, DRELA M, et al. Aerodynamic and aeroacoustic three-dimensional design for a “silent” aircraft[C]//44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virginia: AIAA, 2006. AIAA 2006-241. doi: 10.2514/6.2006-241http://silentaircraft.org/object/download/1931/doc/AIAA-2006-241-725.pdf
[9] MANNEVILLE A, PILCZER D, SPAKOVSZKY Z S. Preliminary evaluation of noise reduction approaches for a functionally silent aircraft[J]. Journal of Aircraft, 2006, 43(3): 836-840. DOI: 10.2514/1.16424
[10] HILEMAN J, REYNOLDS T, DE LA ROSA BLANCO E, et al. Development of approach procedures for silent aircraft[C]//45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virigina: AIAA, 2007. AIAA 2007-451. doi: 10.2514/6.2007-451
[11] DIEDRICH A, HILEMAN J, TAN D, et al. Multidisciplinary design and optimization of the silent aircraft[C]//44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virigina: AIAA, 2006. AIAA 2006-1323. doi: 10.2514/6.2006-1323
[12] HALL C A, CRICHTON D. Engine and installation configurations for a silent aircraft[R]. ISABE 2005-1164. http://silentaircraft.org/object/download/1928/doc/ISABE_2005_1164.pdf
[13] HALL C A, CRICHTON D. Engine design studies for a silent aircraft[J]. Journal of Turbomachinery, 2007, 129(3): 479-487. DOI: 10.1115/1.2472398
[14] DE LA ROSA BLANCO E, HALL C, CRICHTON D. Challenges in the silent aircraft engine design[C]//45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virigina: AIAA, 2007. AIAA 2007-454. doi: 10.2514/6.2007-454
[15] HILEMAN J, SPAKOVSZKY Z, DRELA M, et al. Airframe design for “silent aircraft”[C]//45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. Reston, Virigina: AIAA, 2007. AIAA 2007-453. doi: 10.2514/6.2007-453
[16] MODY P, SATO S, HALL D, et al. Conceptual design of an N+3 hybrid wing body subsonic transport[C]//28th AIAA Applied Aerodynamics Conference, Chicago, Illinois. Reston, Virigina: AIAA, 2010. AIAA 2010-4812. doi: 10.2514/6.2010-4812
[17] KIM H J, LIOU M S. Optimal inlet shape design of N2B hybrid wing body configuration[C]//48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Atlanta, Georgia. Reston, Virigina: AIAA, 2012. AIAA 2012-3917. doi: 10.2514/6.2012-3917
[18] KIM H, LIOU M S. Optimal shape design of mail-slot nacelle on N3-X hybrid wing body configuration[C]//31st AIAA Applied Aerodynamics Conference, San Diego, CA. Reston, Virginia: AIAA, 2013. AIAA 2013-2413. doi: 10.2514/6.2013-2413
[19] DENISOV V, SHKADOV L, CHERNYSHEV S. The flying wing concept - the challenge for the future[C]//AIAA International Air and Space Symposium and Exposition: The Next 100 Years, Dayton, Ohio. Reston, Virginia: AIAA, 2003. AIAA 2003-2887. doi: 10.2514/6.2003-2887
[20] 杨宇飞, 白俊强, 夏露. 飞翼布局运输机气动设计方法研究[J]. 航空计算技术, 2007, 37(1): 22-26. YANG Y F, BAI J Q, XIA L. Aerodynamic design of flying wing transport[J]. Aeronautical Computing Technique, 2007, 37(1): 22-26 (in Chinese).
[21] 宋倩, 万志强. 飞翼式客机机翼气动/结构综合优化方法研究[J]. 民用飞机设计与研究, 2018(4): 6-14. SONG Q, WAN Z Q. Aerodynamic/structural intergrated design for the wing of flying wing airliner[J]. Civil Aircraft Design & Research, 2018(4): 6-14. (in Chinese)
[22] 索欣诗. 翼身融合布局大型客机总体方案综合分析评价与优化[D]. 南京: 南京航空航天大学, 2017. SUO X S. Integrated analysis, evaluation and optimization in conceptual design of blended wing body commercial aircraft[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2017 (in Chinese).
[23] 刘晓静, 吴江浩, 张曙光. 250座级翼身融合布局客机气动设计与优化[J]. 空气动力学学报, 2011, 29(1): 78-84. doi: 10.3969/j.issn.0258-1825.2011.01.013 LIU X J, WU J H, ZHANG S G. Aerodynamic design and optimization of the blended wing body aircraft for 250 passengers[J]. Acta Aerodynamica Sinica, 2011, 29(1): 78-84. (in Chinese) doi: 10.3969/j.issn.0258-1825.2011.01.013
[24] 柴啸, 陈迎春, 谭兆光, 等. 翼身融合布局客机总体参数分析与优化[J]. 航空学报, 2019, 40(9): 623042. CHAI X, CHEN Y C, TAN Z G, et al. Analysis and optimization of overall parameters for blended-wing-body civil aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(9): 623042. (in Chinese)
[25] WHITTENBURY J. Configuration design development of the navy UCAS-D X-47B[C]//AIAA Centennial of Naval Aviation Forum "100 Years of Achievement and Progres", Virginia Beach, VA. Reston, Virigina: AIAA, 2011. AIAA 2011-7041. doi: 10.2514/6.2011-7041
[26] CHAPMAN II COL R E. Unmanned combat aerial vehicles: Dawn of a new age?[J] Aerospace Power Journal, 2002, (2): 60-73. https://www.files.ethz.ch/isn/119927/sum02.pdf
[27] NANGIA R, PALMER M. A comparative study of UCAV type wing planforms - aero performance & stability considerations[C]//23rd AIAA Applied Aerodynamics Conference, Toronto, Ontario, Canada. Reston, Virginia: AIAA, 2005. AIAA 2005-5078. doi: 10.2514/6.2005-5078
[28] 张彬乾, 罗烈, 陈真利, 等. 飞翼布局隐身翼型优化设计[J]. 航空学报, 2014, 35(4): 957-967. ZHANG B Q, LUO L, CHEN Z L, et al. On stealth airfoil optimization design for flying wing configuration[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(4): 957-967. (in Chinese)
[29] 李权, 郭兆电, 雷武涛, 等. 融合体布局超临界翼型设计研究[J]. 空气动力学学报, 2017, 35(4): 579-586. doi: 10.7638/kqdlxxb-2017.0073 LI Q, GUO Z D, LEI W T, et al. Study on supercritical airfoil of blended wing body[J]. Acta Aerodynamica Sinica, 2017, 35(4): 579-586. (in Chinese) doi: 10.7638/kqdlxxb-2017.0073
[30] 郑传宇, 黄江涛, 周铸, 等. 飞翼翼型高维目标空间多学科综合优化设计[J]. 空气动力学学报, 2017, 35(4): 587-597. doi: 10.7638/kqdlxxb-2017.0079 ZHENG C Y, HUANG J T, ZHOU Z, et al. Multidisciplinary optimization design of high dimensional target space for flying wing airfoil[J]. Acta Aerodynamica Sinica, 2017, 35(4): 587-597. (in Chinese) doi: 10.7638/kqdlxxb-2017.0079
[31] PAMBAGJO T, NAKAHASHI K, OBAYASHI S, et al. Aerodynamic design of a medium size blended-wing-body airplane[C]//39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. Reston, Virigina: AIAA, 2001. AIAA 2001-129. doi: 10.2514/6.2001-129
[32] PEIGIN S, EPSTEIN B. Computational fluid dynamics driven optimization of blended wing body aircraft[J]. AIAA Journal, 2006, 44(11): 2736-2745. DOI: 10.2514/1.19757
[33] HILEMAN J I, SPAKOVSZKY Z S, DRELA M, et al. Airframe design for silent fuel-efficient aircraft[J]. Journal of Aircraft, 2010, 47(3): 956-969. DOI: 10.2514/1.46545
[34] LI P F, ZHANG B Q, CHEN Y C, et al. Aerodynamic design methodology for blended wing body transport[J]. Chinese Journal of Aeronautics, 2012, 25(4): 508-516. DOI: 10.1016/s1000-9361(11)60414-7
[35] KUNTAWALA N B, HICKEN J E, ZINGG D W. Preliminary aerodynamic shape optimization of a blended-wing-body aircraft configuration[C]//49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, Florida. AIAA 2011-642. http://oddjob.utias.utoronto.ca/dwz/Miscellaneous/NimeeshaASM2011_FINAL.pdf doi: 10.2514/6.2011-642
[36] REIST T A, ZINGG D W. Aerodynamic shape optimization of a blended-wing-body regional transport for a short range mission[C]//31st AIAA Applied Aerodynamics Conference, San Diego, CA. Reston, Virginia: AIAA, 2013. doi: 10.2514/6.2013-2414
[37] ZHOU L, HUANG J T, GAO Z H, et al. Three-dimensional aerodynamic/stealth optimization based on adjoint sensitivity analysis for scattering problem[J]. AIAA Journal, 2020, 58(6): 2702-2715. DOI: 10.2514/1.J059136
[38] KANAZAKI M, HANIDA R, NARA T, et al. Challenge of design exploration for small blended wing body using unstructured flow solver[J]. Computers & Fluids, 2013, 85: 71-77. DOI: 10.1016/j.compfluid.2012.09.023
[39] REIST T A, ZINGG D W. Aerodynamic design of blended wing-body and lifting-fuselage aircraft[C]//34th AIAA Applied Aerodynamics Conference, Washington, D. C. . Reston, Virginia: AIAA, 2016. AIAA 2016-3874. doi: 10.2514/6.2016-3874
[40] LYU Z J, MARTINS J R R A. Aerodynamic design optimization studies of a blended-wing-body aircraft[J]. Journal of Aircraft, 2014, 51(5): 1604-1617. DOI: 10.2514/1.C032491
[41] LIEBECK R H. Design of the blended wing body subsonic transport[J]. Journal of Aircraft, 2004, 41(1): 10-25. DOI: 10.2514/1.9084
[42] THEODORSEN T. Theory of wing sections of arbitrary shape[R]. NACA-TR-411, 1931. https://digital.library.unt.edu/ark:/67531/metadc66068/m2/1/high_res_d/19930091485.pdf
[43] Theodorsen T, Garrick I E. General potential theory of arbitrary wing sections[R]. NACA-TR-452, 1979. https://ntrs.nasa.gov/api/citations/19800006787/downloads/19800006787.pdf
[44] JACOBS E N, WARD K E, PINKERTON R M. The characteristics of 78 related airfoil sections from tests in the variable-density wind tunnel[R] NACA-TR-460, 1933. https://ntrs.nasa.gov/api/citations/19930091108/downloads/19930091108.pdf
[45] MELVIN R G, HUFFMAN W P, YOUNG D P, et al. Recent progress in aerodynamic design optimization[J]. International Journal for Numerical Methods in Fluids, 1999, 30(2): 205-216. DOI:10.1002/(sici)1097-0363(19990530)30: 2<205: aid-fld827>3.0.co;2-u
[46] GIANNAKOGLOU K C. Design of optimal aerodynamic shapes using stochastic optimization methods and computational intelligence[J]. Progress in Aerospace Sciences, 2002, 38(1): 43-76. DOI: 10.1016/S0376-0421(01)00019-7
[47] LIM D, JIN Y C, ONG Y S, et al. Generalizing surrogate-assisted evolutionary computation[J]. IEEE Transactions on Evolutionary Computation, 2010, 14(3): 329-355. DOI: 10.1109/TEVC.2009.2027359
[48] 唐焕文, 秦学志, 编著. 实用最优化方法[M]. 大连: 大连理工大学出版社, 2004. [49] 张伟, 高正红, 周琳, 等. 基于代理模型全局优化的自适应参数化方法[J]. 航空学报, 2020, 41(10): 123815. ZHANG W, GAO Z H, ZHOU L, et al. Adaptive parameterization method for surrogate-based global optimization[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(10): 123815. (in Chinese)
[50] 王超, 高正红, 张伟, 等. 自适应设计空间扩展的高效代理模型气动优化设计方法[J]. 航空学报, 2018, 39(7): 121745. WANG C, GAO Z H, ZHANG W, et al. Efficient surrogate-based aerodynamic design optimization method with adaptive design space expansion[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(7): 121745. (in Chinese)
[51] PEREZ R E, JANSEN P W, MARTINS J R R A. pyOpt: a Python-based object-oriented framework for nonlinear constrained optimization[J]. Structural and Multidisciplinary Optimization, 2012, 45(1): 101-118. DOI: 10.1007/s00158-011-0666-3
[52] KNOTT E F. A progression of high-frequency RCS prediction techniques[J]. Proceedings of the IEEE, 1985, 73(2): 252-264. DOI: 10.1109/PROC.1985.13137
[53] ZITZLER E, BROCKHOFF D, THIELE L. The hypervolume indicator revisited: On the design of Pareto-compliant indicators via weighted integration[C]//International Conference on Evolutionary Multi-Criterion Optimization, 2007: 862-876. doi: 10.1007/978-3-540-70928-2_64
-
期刊类型引用(6)
1. 范一鸣，李响，张后军. 含冗余控制面飞行器配平优化设计与性能分析. 空气动力学学报. 2024(03): 102-110 . 
本站查看
2. 陈清阳，辛宏博，王鹏，朱炳杰，王玉杰，鲁亚飞. 飞翼布局飞行器研究现状分析. 国防科技大学学报. 2024(03): 39-58 . 百度学术
3. 胡德昭，贾高伟，邵帅，郭正，侯中喜. 无人机气动隐身联合优化的关键技术与研究进展. 无人系统技术. 2024(04): 1-15 . 百度学术
4. 詹韧，贾高伟，郭正，王玲. 协同作战无人机关键能力特征与技术分析. 无人系统技术. 2024(05): 1-12 . 百度学术
5. 赵轲，高正红，周琳，夏露，邓俊，黄江涛. 飞行器气动隐身设计技术研究进展. 航空工程进展. 2024(06): 13-26 . 百度学术
6. Liu ZHANG，Yong HUANG，Zhenglong ZHU，Lihua GAO，Fuzheng CHEN，Fuzhang WU，Meng HE. Virtual flight test of pitch and roll attitude control based on circulation control of tailless flying wing aircraft without rudders. Chinese Journal of Aeronautics. 2023(06): 52-62 . 必应学术
其他类型引用(0)
计量
- 文章访问数: 1245
- HTML全文浏览量: 328
- PDF下载量: 328
- 被引次数: 6
