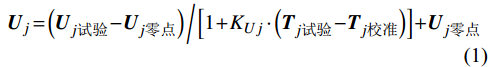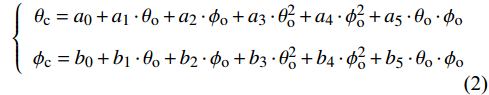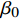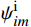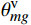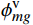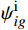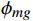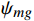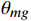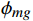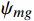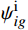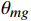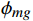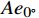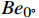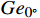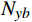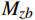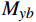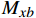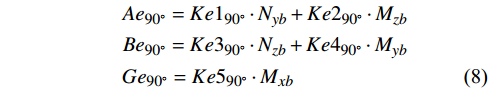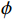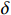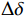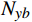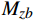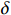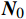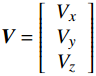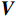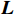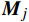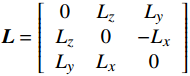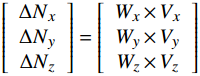Precision force measurement techniques for large aircraft models in 2.4 m continuous transonic wind tunnel
-
摘要:
为满足大飞机研制对风洞测力试验数据精准度的需求，并适应2.4 m连续式跨声速风洞运行特点，中国航空工业空气动力研究院成功研发了多项精细化的测力试验技术。这些技术中，低热膨胀系数高强度天平和天平温度效应补偿与修正技术有效地减小了温度变化对天平数据的影响；角度传感器和视频相结合的直接测量方法与改进后的角度叠加测量方法，均提高了模型姿态角的测量精度；基于线性回归的天平初始载荷计算方法可以一次性获得各种试验状态下的天平初始载荷，并提高气动载荷计算的准确性；基于前后置减振器的主动振动抑制技术能降低模型振动对测量数据的干扰并拓宽迎角范围；弹性变形视频测量与CFD修正技术可以有效分离高雷诺数试验结果中的弹性变形对气动力的影响量。本文对这些试验技术的原理进行了详细介绍，并给出案例证明这些试验技术能够有效提高测力试验的精准度；与ETW 风洞的对比试验显示，大展弦比民机模型的升力系数偏差约0.002，阻力系数偏差约0.0002。
Abstract:To meet the stringent demand for the precision and accuracy in wind tunnel force testing of large aircraft models, Aerodynamics Research Institute of AVIC (Aviation Industry Corporation of China) has innovated several cutting-edge force measurement techniques tailored for the 2.4 m continuous transonic wind tunnel. These techniques include a high-strength and low-thermal-expansion-coefficient balance with the temperature compensation and correction, an attitude angle measurement method using angle sensors and video and a modified method for measuring the attitude angle superposition, a fast calculation method of the initial balance loads under various test conditions based on the linear regression, an active anti-vibration technique based on front and rear damping systems that broadens the range of attack angle, video measurement and CFD (Computational Fluid Dynamics) simulation integrated elastic deformation correction method that effectively isolates the effects of elastic deformation on the aerodynamic forces in high-Reynolds-number tests. This paper delves into the principles underlying these innovative testing techniques and demonstrates their efficacy through case studies. Compared to the European Transonic Windtunnel, our techniques have achieved remarkable improvements in accuracy, with deviations of lift and drag coefficients for a large aspect ratio civil aircraft model being only 0.002 and 0.0002, respectively. These advancements represent a significant step forward in ensuring the reliability and accuracy of wind tunnel testing for large aircraft models.
-
0. 引 言
大飞机研制对风洞测力试验数据精准度提出了非常高的要求，例如：阻力系数的重复性精度需达到0.0001，升力系数的重复性精度需达到0.001；与国外先进风洞的测力试验数据相比，巡航马赫数下，阻力系数偏差应在0.0002以内，升力系数的偏差应在0.002以内。
为了满足这些需求，要求风洞具有优良的流场品质，而连续式跨声速风洞便具有运行时间长、流场品质优良等特点，可以满足大飞机风洞测力试验数据的高精准度水平的必要条件。近年来，我国陆续建造了多座连续式跨声速风洞，其中中国航空工业空气动力研究院（下文简称“航空工业气动院”）的2.4 m连续式跨声速风洞[1]。其流场校测结果表明，该风洞的流场品质达到国际先进水平。
除了对风洞流场品质有要求外，还要求具备高精准度的天平、模型姿态角测量设备和测量方法、数据处理方法。为此，天平的测量精度需达到满量程的0.1%（法向力量程≤15000 N，轴向力量程≤1500 N），模型姿态角的测量精度应不大于0.02°（升力线斜率约1.0/(°)），并且这些设备和方法需要能够适应2.4 m连续式跨声速风洞的运行特点。例如：连续式跨声速风洞马赫数的变化会导致流场温度变化，进而引起模型和天平体的温度变化，因此要求天平输出电压不受温度变化的影响；而且该风洞通过组合控制模型的俯仰角和滚转角得到迎角和侧滑角，这种模型姿态角控制方式具有较高的运行效率，但要求姿态角测量设备和测量方法能够精确测量模型3个方向的姿态角，即俯仰角、偏航角和滚转角。
不同于暂冲式风洞可以在试验间歇采集天平初始载荷，连续式跨声速风洞需要在试验前或试验后一次性采集所有试验状态的天平初始载荷，以保证试验效率。由于无风时的模型角度不等同于试验时的模型角度，故需要准确计算试验时模型姿态角下的天平初始载荷。
当迎角增大到一定程度，模型会发生较为强烈的振动，为了避免模型振动引起的模型姿态及气动力测量精度下降，并扩展试验包线，先进的连续式跨声速风洞一般配备有模型主动振动抑制系统。
2.4 m连续式跨声速风洞具有增压变雷诺数的能力，雷诺数变化的同时，模型机翼外形会发生弹性变形。为了获得真实雷诺数对模型气动力的影响，需要分离模型弹性变形对模型气动力的影响。
针对以上需求，结合2.4 m连续式跨声速风洞的运行特点，航空工业气动院研发了多项精细化测力试验技术，如天平温度效应补偿与修正技术、低热线膨胀系数高强度殷钢天平、角度传感器和视频测量相结合的模型姿态角测量方法、基于局部线性回归的天平初始载荷计算与修正方法、基于压电陶瓷的模型主动振动抑制技术以及基于视频测量与计算流体力学（Computer Fluid Dynamics, CFD）计算的弹性变形影响修正技术等。本文将详细描述这些技术的基本原理，并举例证明这些技术在保证大飞机测力试验数据的精准度上发挥的重要作用。
1. 低温度效应天平技术
1.1 降低天平零点温度效应方法
天平零点温度效应是指温度改变使应变计及其连接导线的电阻发生改变，并使天平体存在温度梯度进而引起热应力，最终导致惠斯通电桥失去平衡，产生零点输出变化。
1.1.1 天平零点温度效应补偿技术
针对天平零点温度效应问题，研究了恒温条件下的相应补偿技术。采取了在惠斯通电桥相应桥臂内串联补偿电阻的零点温度效应补偿技术方案[2-5]，提出了惠斯通电桥桥臂等长的线路布置方法（见图1），引入高分辨率的补偿电阻，控制电阻长度补偿温度效应，确定量化的补偿系数0.0042 µV/V/℃/mm，提升补偿效率50%，实现了风洞天平各电桥零点温度漂移指标优于±0.02 µV/V/℃（见图2）。
1.1.2 低热线膨胀系数高强度殷钢天平
为了探究温度梯度产生的热应力对天平零点温度效应的影响，根据风洞试验的温度梯度条件，应用ANSYS Workbench软件进行了多种天平体材料的热性能参数与天平零点温度效应的相关性分析工作[6-7]。研究结果表明：热线膨胀系数是热应力影响天平零点温度效应的主要因素。以往常用的天平体材料18Ni(250)和17-4PH[8]的热线膨胀系数较大（10.6×10−6/℃），无法满足试验使用要求。经过遴选，发现殷钢材料兼具低热线膨胀系数和高强度，热线膨胀系数和强度标定试验结果表明：其热线膨胀系数为3.5×10−6/℃，抗拉强度为1200 MPa（见图3）。相比于常规天平体材料，殷钢材料的热线膨胀系数降低了约70%，可以有效降低温度梯度条件下的天平零点温度效应，且强度满足风洞试验使用要求。
![]()
图 3 高强度殷钢的热线膨胀系数和强度标定试验Figure 3. Thermal expansion coefficient and strength calibration of high-strength steel1.2 天平灵敏度温度效应修正方法
天平灵敏度温度效应是指温度改变使应变计的灵敏度系数和天平元件材料弹性模量发生变化，导致天平灵敏度变化。现有的天平灵敏度温度效应修正方法[9-10]是对天平工作公式的主项系数进行修正，但这无法完全解决天平体存在温度梯度的问题。针对以上问题，提出了对每个惠斯通电桥的原始数据进行修正，如下式所示：
{\boldsymbol{U}}_{{j}} = \left({\boldsymbol{U}}_{{{j}}试验} - {\boldsymbol{U}}_{{{j}}零点}\right)\bigg/\left[1 + {{K}}_{U{{j}}} \cdot\left({\boldsymbol{T}}_{{{j}}试验} - {\boldsymbol{T}}_{{{j}}校准}\right)\right] + {\boldsymbol{U}}_{{{j}}零点} (1) 其中：Uj试验是试验工况下采集的天平的每个惠斯通电桥输出值；Uj零点是试验前采集的天平的每个惠斯通电桥输出值；KUj是天平的每个惠斯通电桥灵敏度温度修正系数；Tj试验是试验工况下天平每个位置的温度传感器输出值；Tj校准是校准时天平每个位置的温度传感器输出值。
该方法应用于民机模型试验常用的直径80 mm的杆式天平，在变温48 ℃的工况下，通过天平灵敏度温度效应修正，天平综合加载误差达到《风洞应变天平规范》GJB2244A-2011合格指标要求，大部分分量达到先进指标要求（见图4）。
2. 模型姿态角测量技术
2.1 角度传感器和视频相结合的模型姿态角测量方法
在模型姿态角测量方面，航空工业气动院发展了更精细的角度传感器与视频相结合的模型姿态角测量方法，该方法得到的模型俯仰角、偏航角和滚转角的精度介于0.01°～0.02°。具有这样的精度范围主要是因为角度传感器的直接测量精度较高，俯仰角和滚转角的测量精度可达0.01°，但无法测量偏航角；而视频可以测量3个姿态角，但是测量精度相对偏低，俯仰角和偏航角的测量精度为0.02°，滚转角的测量精度为0.05°。另外，传统的角度叠加方法在保证测量精准度的前提下，也可以代替视频，提供偏航角。该方法的原理如下文描述。
在双轴分度仪上，在不同的俯仰角和滚转角组合下标定角度传感器，分别建立俯仰角和滚转角的二元多项式拟合修正关系式：
\left\{\begin{array}{c}{\theta }_{\mathrm{c}} = a_{\mathrm{0}}+a_{\mathrm{1}} \cdot {\theta }_{\mathrm{o}}+a_{\mathrm{2}} \cdot {\phi }_{\mathrm{o}}+a_{\mathrm{3}} \cdot {\theta }_{\mathrm{o}}^{2}+a_{\mathrm{4}} \cdot {\phi }_{\mathrm{o}}^{2}+a_{\mathrm{5}} \cdot {\theta }_{\mathrm{o}} \cdot {\phi }_{\mathrm{o}}\\ {\phi }_{\mathrm{c}} = b_{\mathrm{0}}+b_{\mathrm{1}} \cdot {\theta }_{\mathrm{o}}+b_{\mathrm{2}} \cdot {\phi }_{\mathrm{o}}+b_{\mathrm{3}} \cdot {\theta }_{\mathrm{o}}^{2}+b_{\mathrm{4}} \cdot {\phi }_{\mathrm{o}}^{2}+b_{\mathrm{5}} \cdot {\theta }_{\mathrm{o}} \cdot {\phi }_{\mathrm{o}}\end{array}\right. (2) 式中，下标o代表角度传感器原始测量值，下标c表示角度传感器修正后的测量值。
\alpha_0 和\beta_0 是多项式的常数项，a1、a2、a3、a4、a5、b1、b2、b3、b4、b5是多项式中各项的常数系数。在滚转角0°位置调平模型，角度传感器直接测量俯仰安装角
{\theta }_{im}^{{\rm{i}}} 和滚转安装角{\phi }_{im}^{{\rm{i}}} ，在滚转角90°和- 90°位置调平模型，角度传感器直接测量偏航安装角{\psi }_{im}^{{\rm{i}}} 。角度传感器轴系、模型体轴系、地轴系满足以下矩阵关系式：
\begin{split} &{{{\boldsymbol{R}}}}_{ig} = {{{\boldsymbol{R}}}}_{x}\left({\phi }_{ig}^{{\rm{i}}}\right) \cdot {{{\boldsymbol{R}}}}_{y}\left({\psi }_{ig}^{{\rm{i}}}\right) \cdot {{{\boldsymbol{R}}}}_{z}\left({\theta }_{ig}^{{\rm{i}}}\right) \\ \qquad &{{{\boldsymbol{R}}}}_{im} = {{\boldsymbol{R}}}\left({\phi }_{im}^{{\rm{i}}}\right) \cdot {{\boldsymbol{R}}}\left({\psi }_{im}^{{\rm{i}}}\right) \cdot {{\boldsymbol{R}}}\left({\theta }_{im}^{{\rm{i}}}\right) \\ \qquad &{{{\boldsymbol{R}}}}_{mg} = {{{\boldsymbol{R}}}}_{x}\left({\phi }_{mg}\right) \cdot {{{\boldsymbol{R}}}}_{y}\left({\psi }_{mg}\right) \cdot {{{\boldsymbol{R}}}}_{z}\left({\theta }_{mg}\right)\\ \qquad &{{{\boldsymbol{R}}}}_{ig} = {{{\boldsymbol{R}}}}_{im} \cdot {{{\boldsymbol{R}}}}_{mg} \end{split} (3) 式中，R表示欧拉旋转矩阵；下标i代表角度传感器轴系，下标m代表模型体轴系，下标g代表地轴系；地轴系的x轴为风洞轴线、y轴为铅垂线、z轴为位于水平面垂直于x轴的轴线。
根据关系式（3），可以推导出角度传感器相对于地轴系的偏航安装角
{\psi }_{ig}^{{\rm{i}}} 满足以下关系式：\begin{split} &{{\boldsymbol{R}}}\left({\psi }_{ig}^{{\rm{i}}}\right) = {{\boldsymbol{R}}}(-{\phi }_{ig}^{{\rm{i}}}) \cdot {{\boldsymbol{R}}}\left({\phi }_{im}^{{\rm{i}}}\right) \cdot {{\boldsymbol{R}}}\left({\psi }_{im}^{{\rm{i}}}\right) \cdot \\ &\qquad {{\boldsymbol{R}}}\left({\theta }_{im}^{{\rm{i}}}\right) \cdot {{\boldsymbol{R}}}\left({\phi }_{mg}^{\mathrm{v}}\right) \cdot {{\boldsymbol{R}}}\left({\psi }_{mg}^{\mathrm{v}}\right) \cdot {{\boldsymbol{R}}}\left({\theta }_{mg}^{\mathrm{v}}\right) \cdot {{\boldsymbol{R}}}(-{\theta }_{ig}^{{\rm{i}}})\end{split} (4) 角度传感器直接测量得到角度传感器相对于地轴系的俯仰角
{\theta }_{ig}^{{\rm{i}}} 和滚转角{\phi }_{ig}^{{\rm{i}}} 。视频系统测量得到模型相对于地轴系的俯仰角{\theta }_{mg}^{\mathrm{v}} 、滚转角{\phi }_{mg}^{\mathrm{v}} 、偏航角{\psi }_{mg}^{\mathrm{v}} ，作为初值代入式（4）计算得到{\psi }_{ig}^{{\rm{i}}} ，并参与式（5）的计算：\begin{split} {{{\boldsymbol{R}}}}_{mg} = &{{{\boldsymbol{R}}}}_{x}\left({\phi }_{mg}\right) \cdot {{{\boldsymbol{R}}}}_{y}\left({\psi }_{mg}\right) \cdot {{{\boldsymbol{R}}}}_{z}\left({\theta }_{mg}\right) = {{{\boldsymbol{R}}}}_{mi} \cdot {{{\boldsymbol{R}}}}_{ig} = {{{\boldsymbol{R}}}}_{z}\left(-{\theta }_{im}^{{\rm{i}}}\right) \cdot {{{\boldsymbol{R}}}}_{y}\left(-{\psi }_{im}^{{\rm{i}}}\right) \cdot {{{\boldsymbol{R}}}}_{x}\left(-{\phi }_{im}^{{\rm{i}}}\right){ \cdot {{\boldsymbol{R}}}}_{x}\left({\phi }_{ig}^{{\rm{i}}}\right) \cdot {{{\boldsymbol{R}}}}_{y}\left({\psi }_{ig}^{{\rm{i}}}\right) \cdot {{{\boldsymbol{R}}}}_{z}\left({\theta }_{ig}^{{\rm{i}}}\right) \\ \qquad =&\left[\begin{array}{ccc}\cos\;\psi \cos\;\theta &-\cos\;\psi \sin\;\theta & \sin\;\psi \\ -\sin\;\phi \sin\;\psi \cos\;\theta +\cos\;\phi \sin\;\theta & \sin\;\phi \sin\;\psi \sin\;\theta +\cos\;\phi \cos\;\theta & \sin\;\phi \cos\;\psi \\ -\cos\;\phi \sin\;\psi \cos\;\theta -\sin\;\phi \sin\;\theta & \cos\;\phi \sin\;\psi \sin\;\theta -\sin\;\phi \cos\;\theta & \cos\;\phi \cos\;\psi \end{array}\right] \end{split} (5) 得到模型体轴系相对于地轴系的俯仰角
{\theta }_{mg} 、滚转角{\phi }_{mg} 、偏航角{\psi }_{mg} ：\left\{\begin{array}{l}{\psi }_{mg} = {\mathit{\sin}}^{-1}\left(\sin\;\psi \right)\\ {\phi }_{mg} = {\mathit{\sin}}^{-1}\left(\dfrac{\sin\;\phi \cos\;\psi }{\cos\;{\psi }_{mg}}\right)\\ {\theta }_{mg} = {\mathit{\sin}}^{-1}\left(\dfrac{\cos\;\psi \sin\;\theta }{\cos\;{\psi }_{mg}}\right)\end{array}\right. (6) 再次将俯仰角
{\theta }_{mg} 、滚转角{\phi }_{mg} 、偏航角{\psi }_{mg} 作为初值，计算角度传感器相对于地轴系的偏航安装角{\psi }_{ig}^{{\rm{i}}} 。多轮迭代计算，直到新旧俯仰角{\theta }_{mg} 、滚转角{\phi }_{mg} 、偏航角{\psi }_{mg} 的偏差在0.001°以内为止。2.2 改进的角度叠加模型姿态角测量方法
对于单支撑测力试验，常用的一种模型姿态角测量方法是角度叠加方法，即将支撑机构在地轴系的角度、支杆和支撑机构的安装角、支杆前端轴线和后端轴线间的夹角、天平和支杆的安装角、天平/支杆/支撑的弹性角、模型和天平的安装角进行叠加，得到模型在地轴系下的姿态角。航空工业气动院在2.4 m连续式跨声速风洞中使用此方法时发现，以往的天平/支杆/支撑的弹性角、模型和天平的安装角的测量和计算方法存在偏差，影响了试验数据的准确性。
2.4 m连续式跨声速风洞的支撑装置包括俯仰角和滚转角机构（见图5）。在不同的模型迎角和侧滑角的组合下，尽管天平和支杆的相对角度不变，但是支杆相对于支撑滚转，两者之间的夹角在试验中是根据迎角和侧滑角需求而变化的，故模型的法向力与支撑的纵向中心面夹角也是变化的。当法向力与支撑的纵向中心面夹角较大时，法向力在支撑横向的分量较大，而由于支撑的横向刚度较小，故支撑的横向变形量较大。仅测量天平和支杆的弹性角系数已不足以代表天平、支杆和支撑的整体弹性角系数，因而将对模型姿态角测量结果的准确性产生影响。为此，需要测量与计算天平、支杆、支撑的整体弹性角系数。
![]()
图 5 2.4 m连续式跨声速风洞的天平、支杆和支撑组成的支撑系统Figure 5. Support system in 2.4 m continuous transonic wind tunnel另外，由于加工误差会导致模型和天平装配后，模型轴和天平轴不同心或扭转，使模型和天平之间存在安装角，进而导致天平校准时存在误差。试验结果表明，当模型和天平之间的安装角达到0.02°以上时，其产生的影响不可忽略。
因此，为了进一步提高角度叠加方法的准确性，分别针对天平/支杆/支撑的弹性角、模型和天平的安装角提出了改进的计算与测量方法。
2.2.1 天平/支杆/支撑的弹性角计算方法改进
当支杆和支撑相对夹角为0°，弹性角计算公式如下：
\begin{split}&{Ae}_{0^\circ } = {Ke}_{{{N}}_{y}0^\circ } \cdot {N}_{yb}+{Ke}_{{M}_{z}0^\circ } \cdot {M}_{zb}\\ \qquad &{Be}_{0^\circ } = {Ke}_{{N}_{z}0^\circ } \cdot {N}_{zb}+{Ke}_{{M}_{y}0^\circ } \cdot {M}_{yb} \\ \qquad &{Ge}_{0^\circ } = {Ke}_{{M}_{x}0^\circ } \cdot {M}_{xb}\end{split} (7) 式中：
{Ae}_{0^\circ } 、{Be}_{0^\circ } 、{Ge}_{0^\circ } 分别为利用支杆和支撑相对夹角为0°时的弹性角系数计算得到的风洞试验的纵向弹性角、横向弹性角、滚转弹性角，Ke为弹性角系数；{N}_{yb} 为天平法向力，{M}_{zb} 为天平俯仰力矩；{N}_{zb} 为天平横向力；{M}_{yb} 为天平偏航力矩，{M}_{xb} 为天平滚转力矩。同理，当支杆和支撑相对夹角为90°，弹性角计算公式如式（8）：
\begin{split}&{Ae}_{90^\circ } = {Ke1}_{90^\circ } \cdot {N}_{yb}+{Ke2}_{90^\circ } \cdot {M}_{zb} \\ \qquad &{Be}_{90^\circ } = {Ke3}_{90^\circ } \cdot {N}_{zb}+{Ke4}_{90^\circ } \cdot {M}_{yb}\\ \qquad &{Ge}_{90^\circ } = {Ke5}_{90^\circ } \cdot {M}_{xb}\end{split} (8) 当支杆和支撑之间存在滚转角
\phi ，支撑、支杆和天平的纵向弹性角、横向弹性角和滚转弹性角的计算公式如式（9）：{Ae}_{\mathrm{\phi }} = \mathrm{a}\mathrm{t}\mathrm{a}\mathrm{n}\left(\sqrt{{\left[\mathrm{tan}\left(\mathrm{s}\mathrm{g}\mathrm{n}\left({Ae}_{0^\circ }\right) \cdot \left|{Ae}_{0^\circ } \cdot \mathrm{cos}\;\phi \right|\right)\right]}^{2}+{\left[\mathrm{tan}\left(\mathrm{s}\mathrm{g}\mathrm{n}\left({Ae}_{90^\circ }\right) \cdot \left|{\mathit{Ae}}_{90^\circ } \cdot \mathrm{sin}\;\phi \right|\right)\right]}^{2}}\right) {Be}_{\mathrm{\phi }} = \mathrm{a}\mathrm{t}\mathrm{a}\mathrm{n}\left(\sqrt{{\left[\mathrm{tan}\left(\mathrm{s}\mathrm{g}\mathrm{n}\left({Be}_{0^\circ }\right) \cdot \left|{Be}_{0^\circ } \cdot \mathrm{cos}\;\phi \right|\right)\right]}^{2}+{\left[\mathrm{tan}\left(\mathrm{s}\mathrm{g}\mathrm{n}\left({Be}_{90^\circ }\right) \cdot \left|{\mathit{Be}}_{90^\circ } \cdot \mathrm{sin}\;\phi \right|\right)\right]}^{2}}\right) {Ge}_{\mathrm{\phi }} = \mathrm{a}\mathrm{t}\mathrm{a}\mathrm{n}\left(\sqrt{{\left[\mathrm{tan}\left(\mathrm{s}\mathrm{g}\mathrm{n}\left({Ge}_{0^\circ }\right) \cdot \left|{Ge}_{0^\circ } \cdot \mathrm{cos}\;\phi \right|\right)\right]}^{2}+{\left[\mathrm{tan}\left(\mathrm{s}\mathrm{g}\mathrm{n}\left({Ge}_{90^\circ }\right) \cdot \left|{Ge}_{90^\circ } \cdot \mathrm{sin}\;\phi \right|\right)\right]}^{2}}\right) (9) 以大展弦比民机模型在2.4 m连续式跨声速风洞中的横航向测力试验为例，对比分析分别采用夹角0°的弹性角系数（即未修正支撑的横向弹性角）和本文提出的不同滚转夹角的弹性角系数（即修正支撑的横向弹性角）时，两者对大展弦比民机模型的测力数据曲线的影响，结果见图6。其中，马赫数Ma = 0.75，雷诺数Re = 3×106（平均气动弦长0.1928 m）。从图中可看到，对于阻力系数、升力系数和俯仰力矩系数，在迎角1°附近支撑系统的横向弹性变形影响最大；当迎角相同时，阻力系数、升力系数、俯仰力矩系数的最大偏差分别达到0.00002、0.0073、0.0014。对于横向力系数、滚转力矩系数和偏航力矩系数，在迎角2°附近支撑系统的横向弹性变形影响最大，三者的最大偏差分别为0.0001、0.0005、0.00002。与国军标先进指标相比（见表1），在相同迎角下，横向弹性变形修正前后的阻力系数偏差超过国军标先进指标，修正前后的升力系数偏差、俯仰力矩系数偏差、滚转力矩系数偏差超过国军标合格指标。由此可见，支撑系统的横向弹性变形的影响不可忽略，为获得更准确的模型姿态角，支撑系统的横向弹性变形影响修正是必须的。
![]()
图 6 Ma = 0.75、Re = 3×106，支撑系统横向弹性变形对大展弦比民机模型气动力系数的影响Figure 6. Variations of aerodynamic coefficients of a large aspect ratio civil aircraft model with the lateral elastic deformation of the support system at Ma = 0.75 and Re = 3×106表 1 测力试验数据重复性精度国军标指标Table 1. GJB criteria of the repeatability accuracy of force measurement data阻力系数
均方根偏差\delta_{C_x}升力系数
均方根偏差\delta_{C_y}俯仰力矩系数
均方根偏差\delta_{C_{mz}}合格指标 0.0005 0.0020 0.0010 先进指标 0.0001 0.0008 0.0003 横向力系数
均方根偏差\delta_{C_z}滚转力矩系数
均方根偏差\delta_{C_{mx}}偏航力矩系数
均方根偏差\delta_{C_{my}}合格指标 0.00080 0.00020 0.00020 先进指标 0.00015 0.00005 0.00008 2.2.2 模型和天平的安装角测量方法改进
传统上通过天平力计算模型和天平之间的安装角，这种方法得到的安装角的准确性依赖于天平力的精准度。但是，实际上天平校准存在偏差，如加载头弹性变形引起的角度偏差。为了避免校准偏差的干扰，模型和天平之间的安装角可以包含天平校准偏差，即此时安装角包括固有安装角和弹性安装角两部分。以模型和天平之间的俯仰安装角为例，可表示为式（10）：
{\theta }_{mb} = \delta +\Delta \delta = \delta +A \cdot {N}_{yb}+B \cdot {M}_{zb} (10) 式中，
\delta 是固有安装角，弹性安装角\Delta \delta 是天平法向力{N}_{yb} 和俯仰力矩{M}_{zb} 的二元线性函数，A和B为系数。准确的模型和天平之间的俯仰安装角可以使模型调平后，天平力在模型轴线上的投影之和为零，即满足以下关系式：
\begin{split}& {N}_{yb} \cdot \mathrm{sin}\;{\theta }_{mb}+{N}_{xb} \cdot \mathrm{cos}\;{\theta }_{mb} = 0 \\&\qquad {\theta }_{mb} = -\mathrm{a}\mathrm{t}\mathrm{a}\mathrm{n}\left(\frac{{N}_{xb}}{{N}_{yb}}\right) \end{split} (11) 在模型上的两个不同位置阶梯加载，通过二元线性回归求解式（10）中的系数A、B及
\delta 。事实证明，在加载范围内，这些系数可以使天平力在模型轴线上的投影之和为零，见图7。![]()
图 7 修正模型和天平之间的安装角后，天平力在模型轴线上的投影之和Figure 7. Summation of the projected balance forces on the model axis after the correction of the installation angle between model and balance仍然以大展弦比民机模型在2.4 m连续式跨声速风洞中的横航向测力试验为例，使用本文介绍的方法，计算得到模型和天平之间的固定安装角为0.033°、弹性安装角的法向力系数为−0.00166(°)/kN、俯仰力矩系数为−0.007292(°)/(
{\rm{kN}}\cdot {\rm{m}} )。未修正和修正弹性安装角对大展弦比民机模型的测力数据曲线的影响见图8、图9。从图中可以看到，是否修正弹性安装角对除升阻力系数以外的各项气动力系数均有较大影响，迎角越大影响越明显；随着迎角增大，阻力系数、升力系数、俯仰力矩系数、横向力系数、滚转力系数、偏航力矩系数的曲线斜率均增大。模型和天平之间的安装角是固有角度，与纵向试验或横向试验无关，故对于纵横向测力试验，均需修正弹性安装角。![]()
图 8 Ma = 0.75、Re = 3×106，弹性安装角对大展弦比民机模型气动力系数曲线的影响Figure 8. Variations of aerodynamic coefficients of a large aspect ratio civil aircraft model with the elastic installation angle at Ma = 0.75 and Re = 3×106![]()
图 9 Ma = 0.75、Re = 3×106，弹性安装角对大展弦比民机模型极曲线的影响Figure 9. Variations of polar curves of a large aspect ratio civil aircraft model with the elastic installation angle at Ma = 0.75 and Re = 3×106![]()
图 10 Ma = 0.75、Re = 3×106，不同模型姿态角测量方法对大展弦比民机模型气动力系数曲线的影响Figure 10. Variations of aerodynamic coefficients of a large aspect ratio civil aircraft model with the model attitude angle obtained by different measurement methods at Ma = 0.75 and Re = 3×1062.3 两种模型姿态角测量方法的准确性验证
为了验证前述两种模型姿态角测量方法的准确性，利用大展弦比民机模型，在Ma = 0.75、Re = 3×106的定侧滑角变迎角试验中，对比分析了分别使用传统的角度叠加、改进的角度叠加、角度传感器和视频相结合3种模型姿态角测量方法对各气动力系数的影响 ，结果如图10所示。角度传感器和视频相结合方法得到的模型迎角与改进的角度叠加方法得到的模型迎角的偏差在0.02°以内。相较于传统的角度叠加方法，改进的角度叠加方法与角度传感器和视频相结合的方法得到的阻力系数、升力系数和俯仰力矩系数曲线的差距非常小，相同迎角下三者的偏差分别小于0.0002、0.001、0.0002。这证明角度传感器和视频相结合的方法与改进的角度叠加方法能够提高模型姿态角的测量精准度。
3. 天平初始载荷计算
3.1 基于线性回归的天平初始载荷计算方法
2.4 m连续式跨声速风洞的姿态角控制方式是通过俯仰和滚转耦合实现模型的姿态角变化。在无风测试中发现，在不同姿态角下，天平测量的各方向初始载荷并不等同于模型和天平的自重在该方向的分量；并且试验时的姿态角也不等同于无风测试的姿态角，故无法直接使用无风测试的初始载荷作为试验状态的初始载荷。所以2.4 m连续式跨声速风洞长时间连续运行要求试验前或试验后一次性采集所有的天平初始载荷。为此，航空工业气动院参考美国NTF的天平初始载荷计算方法[11]，研发了基于线性回归的天平初始载荷测量与计算方法[12]。
有风状态下的自重力向量
{{{\boldsymbol{N}}}}_{0} 与无风状态下第j模型姿态角的自重力向量{{{\boldsymbol{N}}}}_{j} 的差量为：\Delta {{\boldsymbol{N}}} = {{{\boldsymbol{N}}}}_{0}-{{{\boldsymbol{N}}}}_{j} = W{{\boldsymbol{V}}} (12) 令
\Delta {{\boldsymbol{N}}} = \left[\begin{array}{c}{\Delta N}_{x}\\ {\Delta N}_{y}\\ {\Delta N}_{z}\end{array}\right] ，{{\boldsymbol{V}}} = \left[\begin{array}{c}{V}_{x}\\ {V}_{y}\\ {V}_{z}\end{array}\right] ，则有\scriptsize{{{\boldsymbol{V}}} = \left[ \begin{array}{c} - \cos\;{\psi }_{0}\sin\;{\theta }_{0} + \cos\;{\psi }_{j}\sin\;{\theta }_{j}\\ \sin\;{\phi }_{0}\sin\;{\psi }_{0}\sin\;{\theta }_{0} + \cos\;{\phi }_{0}\cos\;{\theta }_{0} - \left(\sin\;{\phi }_{g}\sin\;{\psi }_{j}\sin\;{\theta }_{j} + \cos\;{\phi }_{j}\cos\;{\theta }_{j}\right)\\ \cos\;{\phi }_{0}\sin\;{\psi }_{0}\sin\;{\theta }_{0} - \sin\;{\phi }_{0}\cos\;{\theta }_{0} - \left(\cos\;{\phi }_{j}\sin\;{\psi }_{j}\sin\;{\theta }_{j}-\sin\;{\phi }_{j}\cos\;{\theta }_{j}\right)\end{array} \right]} 其中
{{\boldsymbol{V}}} 为试验即有风状态下的模型姿态角和无风状态下第j个模型姿态角建立的角度函数向量。天平力与模型姿态角的函数{{\boldsymbol{V}}} 的关系式符合一元线性回归模型，可以求解出天平力对应的自重W。当天平校心和模型重心不重合时，通过两心距平移矩阵
{{\boldsymbol{L}}} ，计算得到有风姿态下的自重力矩向量{\boldsymbol{M}}_{0} 与无风状态第j个模型姿态角下的自重力矩向量{{{\boldsymbol{M}}}}_{j} 的差量：\Delta {{\boldsymbol{M}}} = {{\boldsymbol{L}}} \cdot \Delta {{\boldsymbol{N}}} (13) 其中，
{\boldsymbol{L}}= \left[\begin{array}{ccc}0& {L}_{z}& {L}_{y}\\ {L}_{z}& 0& -{L}_{x}\\ {L}_{y}& {L}_{x}& 0\end{array}\right] ，即\left[\begin{array}{c}{\Delta M}_{x}\\ {\Delta M}_{y}\\ {\Delta M}_{z}\end{array}\right] = \left[\begin{array}{ccc}0& {L}_{z}& {L}_{y}\\ {L}_{z}& 0& -{L}_{x}\\ {L}_{y}& {L}_{x}& 0\end{array}\right]\left[\begin{array}{c}{\Delta N}_{x}\\ {\Delta N}_{y}\\ {\Delta N}_{z}\end{array}\right] (14) 代入
\left[\begin{array}{c}{\Delta N}_{x}\\ {\Delta N}_{y}\\ {\Delta N}_{z}\end{array}\right] = \left[\begin{array}{c}{W}_{x}\times {V}_{x}\\ {W}_{y}\times {V}_{y}\\ {W}_{z}\times {V}_{z}\end{array}\right] ，得到下式：\left[\begin{array}{c}{\Delta M}_{x}\\ {\Delta M}_{y}\\ {\Delta M}_{z}\end{array}\right] = \left[\begin{array}{c}{W}_{y}\times {V}_{y}\times {L}_{z}+{W}_{z}\times {V}_{z}\times {L}_{y}\\ {W}_{x}\times {V}_{x}\times {L}_{z}-{W}_{z}\times {V}_{z}\times {L}_{x}\\ {W}_{x}\times {V}_{x}\times {L}_{y}+{W}_{y}\times {V}_{y}\times {L}_{x}\end{array}\right] (15) 式（15）符合二元线性回归模型，可以求解出天平力矩对应的自重W。
试验状态的天平初始载荷按照图11所示的流程进行计算和修正。
![]()
图 11 天平初始载荷计算与修正的流程Figure 11. Calibration and correction process of the initial balance load3.2 全局线性回归和局部线性回归对比分析
在初始载荷采集阶段，对民机模型在不同姿态角下的天平数据进行回归分析，包括本象限滚转角的局部线性回归和多个象限滚转角的全局线性回归，两者的天平轴向力相关系数R2有明显差异，图12所示为不同滚转角范围下天平轴向力线性回归相关系数R2对比结果。在全局滚转角−90°～90°，天平轴向力线性回归的相关系数R2小于局部滚转角−90°～0°或0°～90°的天平轴向力线性回归的相关系数R2。
![]()
图 12 不同滚转角范围线性回归结果对比Figure 12. Comparison of linear regression results in different rolling angle ranges在大展弦比民机模型试验中分别采用全局线性回归和局部线性回归方法计算试验状态下的天平初始载荷。对于马赫数Ma = 0.75、雷诺数Re = 3×106的定侧滑角变迎角试验，由于局部线性回归方法提高了天平力线性回归的相关系数，故初始载荷计算的准确性提高。相较于全局线性回归方法，在2.4 m连续式跨声速风洞中使用局部线性回归方法得到的民机模型的阻力系数曲线与相同模型在ETW风洞中获得的阻力系数曲线更为接近，两种方法的阻力系数偏差达到0.0002～0.0003，如图13所示。
![]()
图 13 Ma = 0.75、Re = 3×106，全局线性回归和局部线性回归的阻力系数曲线Figure 13. Global and local linear regressions of drag coefficients at Ma = 0.75 and Re = 3×1064. 主动振动抑制技术
大飞机模型在进行亚跨声速风洞试验时，非常容易发生低频振动，这将降低迎角和天平的测量精度，限制了试验迎角范围，严重时会影响风洞运行安全。
国内外先进风洞主动振动抑制技术的基本原理是通过阻尼器施加反向作用力抵消振动载荷。阻尼器的核心元件通常采用电机或压电陶瓷，通过电机或压电陶瓷高频作动产生作动力。例如，NTF风洞采用压电陶瓷作为阻尼器的执行元件[13]，ETW风洞的前置和后置减振器分别采用以压电陶瓷和电机为核心的阻尼器[14]。考虑到压电陶瓷具有比电机更高的作动频率且相同体积内可产生更大的作动力，航空工业气动院2.4 m连续式跨声速风洞的前置和后置减振器均采用压电陶瓷作为阻尼器的核心执行元件。
该风洞的主动振动抑制系统适用于多阶频率和模态的振动，其组成如图14所示，由前置和后置减振器及控制系统组成。前置减振器安装于天平和支杆前端之间，后置减振器安装于支杆后端和弯刀之间；加速度计粘贴在模型和支杆前端，用于测量模型的振动情况。控制器有AI、AO通道，具备采集、运算和输出控制信号的功能。
通过地面敲击测试确定系统的固有频率和阻尼比，采用系统辨识方法根据系统固有频率和阻尼比建立仿真模型，采用经典控制理论进行仿真调试，选取最优控制参数。图15为采用经典控制理论仿真得到的结果，在第0 s对系统施加正弦激励，第2 s投入控制，可见在投入控制后系统的加速度随时间衰减，达到了振动抑制的效果。
针对特定频率范围进行振动抑制系统调试，参照仿真得到的最优控制参数进行微调，根据模型的模态特性确定前后置减振器对各阶模态的控制作用及控制力的分配，针对一二阶模态使用前后置减振器分别控制、组合控制验证控制效果，获取控制效果较好的参数。风洞试验过程中，振动抑制系统以加速度计信号作为反馈，控制器计算后得到控制信号，根据振动幅度和频率、前后置减振器位置、结构形式和输出能力的不同，在分组和坐标变换后，给前后置减振器的压电陶瓷分配不同功放，使其输出不同电压值，进而驱动安装在前置和后置减振器中的压电陶瓷按规律作动，实现对模型振动的有效抑制。振动抑制控制系统框图如图16所示。
大展弦比民机模型在常压、马赫数Ma = 0.75、迎角从−4°连续变化到4°的试验条件下，未开启与开启前后置减振器的模型振动情况对比如图17所示。可见未开启减振器时，模型的振动幅值（加速度波动的最大值）达到0.7 g，而开启减振器时约为0.35 g，衰减约50%；升力随时间变化曲线的振荡幅度变小（见图18），迎角范围拓展了约1°（见图19）。
![]()
图 17 Ma = 0.75，未开启和开启前后置减振器的模型振动情况对比Figure 17. Comparison of the model vibration without and with the anti-vibration system at Ma = 0.75![]()
图 18 Ma = 0.75，减振器对降低升力随时间变化曲线振荡幅度的作用Figure 18. Effect of the anti-vibration system on the temporal lift oscillation at Ma = 0.75![]()
图 19 Ma = 0.75 减振器对拓展迎角范围的作用Figure 19. Effect of anti-vibration system on the range ofattack angle5. 机翼弹性变形修正技术
5.1 弹性变形修正方法
对于拥有大展弦比机翼的飞机，即使采用高强度合金钢制作的风洞模型，在气动载荷的作用下模型依然会产生较大的静弹性变形。风洞试验过程中天平测得的试验数据为变形后的气动力数据，与期望的刚性外形气动数据之间存在差异，因此需要对试验数据进行修正。本文机翼弹性变形修正采用风洞试验形变测量与CFD相结合的方法。
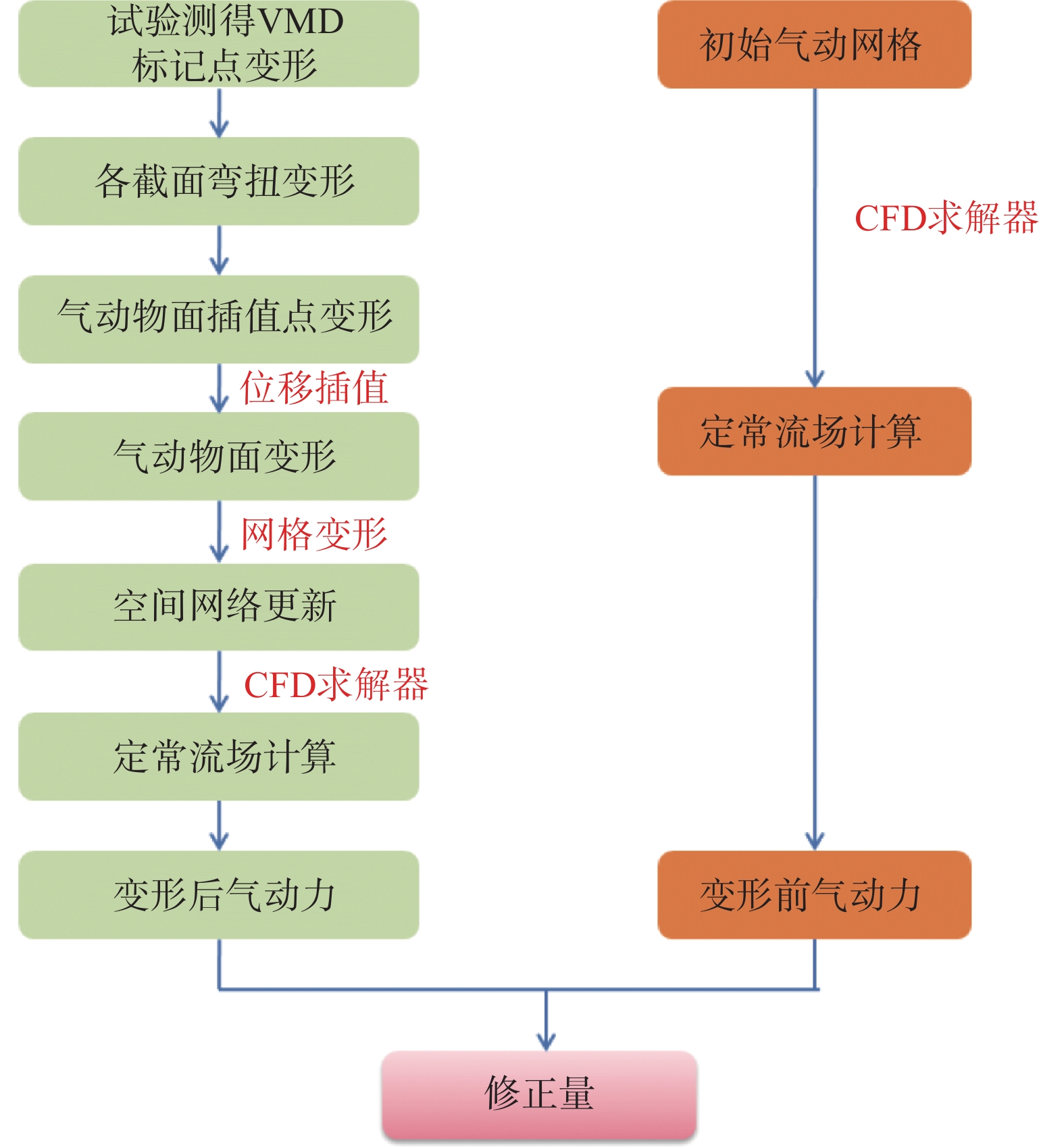
建立刚性外形下的气动计算网格，基于试验测得的弯扭形变结果，利用数据插值和网格变形方法自动构建模型变形后的计算网格；然后采用CFD手段分别计算刚性外形和变形后外形的气动力，两者的差量即为机翼静弹性变形对气动力的影响量；最后利用该差量对风洞试验数据进行修正，得到刚性外形气动力。变形修正计算流程如图20所示。
在形变测量方面，航空工业气动院研发了丝网印刷荧光特征标记点，配合激发光源使用，视频图像清晰度满足测量要求，见图21。荧光标记点的厚度约20 μm，远小于传统的纸质标记点厚度，对测力试验数据几乎无影响，视频测量的精度达到0.1 mm。
![]()
图 21 形变测量与CFD相结合的弹性变形修正计算流程Figure 21. Elastic deformation correction process based on video measurement and CFD在气动力求解方面，选用气动院自研的非结构网格软件平台UNSMB/结构网格软件平台ENSMB[15-16]，数值求解三维定常Navier-Stokes 方程，并通过多重网格技术和并行计算技术提高计算效率。经大量工程算例验证，这两款计算软件具有较好的计算精度。
在变形后的外形重构方面，以刚性网格为基础，首先根据试验测得的形变结果，采用高精度的RBF数据插值方法更新物面网格，保证变形后的物面网格具有较高的质量与精度；其次采用RBF&TFI/RBF& Delaunay混合网格变形方法[17-18]自动生成变形后的空间网格。该方法一方面具有较高的效率，一方面能保证变形前后网格拓扑的一致性，可以很好地消除网格拓扑差异对计算结果的影响。
5.2 算例验证
采用有试验数据的大展弦比民机模型对弹性变形修正方法的有效性进行了验证。图22为刚性外形计算网格，采用黏性结构网格，第一层网格高度为参考弦长的1×10−6倍，保证y+在1左右。
图23为马赫数Ma = 0.75、雷诺数Re = 3×106、迎角2°工况下，该民机模型在ETW风洞和航空工业气动院FL-62风洞中的形变测量结果对比。从图中可以看出，FL-62风洞弯扭变形测量结果与ETW风洞测量结果趋势一致，数值上也较为吻合。
![]()
图 23 ETW和AVIC的形变测量结果对比Figure 23. Comparisons of bend and twsit deformations measured by ETW and AVIC对于变雷诺数试验，除了雷诺数外，模型弹性变形对气动力系数的影响也是显著的。图24给出了马赫数Ma = 0.75，不同雷诺数对升力系数和阻力系数的影响（图中数据为Re = 8×106时的值减去Re = 3×106时的值），即雷诺数变化产生的升力系数差量和阻力系数差量。图中黑色曲线为试验结果，红色曲线为计算结果，对比计算和试验结果发现，两者的升力系数差量的差异基本在0.003以内，阻力系数差量的差异基本在0.0005以内。引起差异的主要原因是计算时未涉及模型弹性变形，忽略了其对气动力系数的影响，而试验中模型实际上是发生了弹性变形的。
![]()
图 24 不同雷诺数下试验与CFD计算得到的升阻力系数差量对比曲线Figure 24. Lift and drag coefficients obtained by experiments and CFD simulations at different Reynolds numbers图25为马赫数Ma = 0.75、雷诺数Re = 8×106工况下，计算所得的模型弹性变形前后气动力与试验结果的对比。图26为试验测得的沿机翼展向分布的弯扭变形。从图27中可以看出，弹性变形使得机翼产生负扭转，机翼剖面当地迎角降低，计算所得的变形后气动力减小，与试验数据更加接近。结合图28中数据可以看出，升力系数最大修正量约为−0.032，阻力系数最大修正量约为−0.00398。此外，图27和图28的数据还显示，本文试验结果与该模型在ETW中相同状态的试验结果数据吻合度较高，两座风洞的升力系数偏差约0.002，阻力系数偏差约0.0002。
![]()
图 25 计算所得的民机模型弹性变形前后气动力与试验数据对比Figure 25. Comparison of aerodynamic force coefficients before and after elastic deformation of a civil aircraft model between experimental and computational data![]()
图 26 民机模型弯扭变形沿机翼展向分布Figure 26. Distributions of the bending and twisting deformation along the spanwise direction of the wing of a civil aircraft model![]()
图 27 Ma = 0.75、Re = 3×106，大展弦比民机模型在FL-62和ETW的升力系数曲线Figure 27. Comparisons of lift coefficients of a large aspect ratio civil aircraft model measured by ETW and AVIC at Ma = 0.75 and Re = 3×106![]()
图 28 Ma = 0.75、Re = 3×106，大展弦比民机模型在FL-62和ETW试验的阻力系数曲线Figure 28. Comparisons of drag coefficients of a large aspect ratio civil aircraft model measured by ETW and AVIC at Ma = 0.75 and Re = 3×1066. 结 论
航空工业气动院为适应2.4 m连续式跨声速风洞运行特点而研发了多项试验技术，并利用大展弦比民机模型对各项技术进行了试验验证，得到以下结论：
1） 经过零点温度效应补偿的低线性膨胀系数高强度殷钢天平具有极低的温度效应和良好的零点电压稳定性，精度为±0.02 μV/V/℃，加之零点温度效应补偿和灵敏度温度效应修正，保证风洞长时间运行零点电压稳定以及天平输出电压不受流场温度变化的影响，天平力和力矩的精度达到满量程的0.1%水平。
2） 对于模型姿态角测量，角度传感器和视频相结合的直接测量方法与改进的角度叠加方法，两种方法测得的模型迎角偏差在0.02°以内。
3） 局部线性回归方法可以有效提高模型试验状态下的天平初始载荷的计算准确性，从而进一步提高气动力数据计算的准确性。
4） 采用模型主动振动抑制技术，改善了测力数据的精度，拓宽了试验迎角的范围。
5） 弹性变形视频测量与CFD修正技术，分离出了弹性变形对试验数据的影响，有效提高了高雷诺数下测力试验数据的准确性。
6） 2.4 m连续式跨声速风洞的测力试验数据精度达到或接近《高速风洞和低速风洞测力实验精度指标》（GJB 1061-91）的先进指标要求（详细数据见表2）。
表 2 2.4 m连续式跨声速风洞民机模型测力试验数据重复性精度（Re = 3×106）Table 2. Repeatability accuracy of force measurement data of a civil aircraft model (Re = 3×106)阻力系数
均方根偏差\delta_{C_x}升力系数
均方根偏差\delta_{C_y}俯仰力矩系数
均方根偏差\delta_{C_{mz}}合格指标 0.00050 0.00200 0.00100 先进指标 0.00010 0.00080 0.00030 Ma=0.5 0.00004 0.00030 0.00017 Ma=0.75 0.00002 0.00016 0.00015 Ma=0.8 0.00004 0.00033 0.00019 Ma=0.9 0.00009 0.00030 0.00017 横向力系数
均方根偏差\delta_{C_z}滚转力矩系数
均方根偏差\delta_{C_{mx}}偏航力矩系数
均方根偏差\delta_{C_{my}}合格指标 0.00080 0.00020 0.00020 先进指标 0.00015 0.00005 0.00008 Ma=0.5 0.00016 0.00001 0.00001 Ma=0.75 0.00017 0.00001 0.00001 Ma=0.8 0.00021 0.00002 0.00001 Ma=0.9 0.00027 0.00002 0.00002 2.4 m连续式跨声速风洞与这些精细化的测力试验技术相结合，进一步提升了该风洞的测力试验水平，有效地保证了用于大飞机设计与验证的测力数据质量。另外，这些测力试验技术不局限于2.4 m连续式跨声速风洞，也可以适用于其他先进的连续式风洞。
-
![]()
图 3 高强度殷钢的热线膨胀系数和强度标定试验
Figure 3. Thermal expansion coefficient and strength calibration of high-strength steel
![]()
图 5 2.4 m连续式跨声速风洞的天平、支杆和支撑组成的支撑系统
Figure 5. Support system in 2.4 m continuous transonic wind tunnel
![]()
图 6 Ma = 0.75、Re = 3×106，支撑系统横向弹性变形对大展弦比民机模型气动力系数的影响
Figure 6. Variations of aerodynamic coefficients of a large aspect ratio civil aircraft model with the lateral elastic deformation of the support system at Ma = 0.75 and Re = 3×106
![]()
图 7 修正模型和天平之间的安装角后，天平力在模型轴线上的投影之和
Figure 7. Summation of the projected balance forces on the model axis after the correction of the installation angle between model and balance
![]()
图 8 Ma = 0.75、Re = 3×106，弹性安装角对大展弦比民机模型气动力系数曲线的影响
Figure 8. Variations of aerodynamic coefficients of a large aspect ratio civil aircraft model with the elastic installation angle at Ma = 0.75 and Re = 3×106
![]()
图 9 Ma = 0.75、Re = 3×106，弹性安装角对大展弦比民机模型极曲线的影响
Figure 9. Variations of polar curves of a large aspect ratio civil aircraft model with the elastic installation angle at Ma = 0.75 and Re = 3×106
![]()
图 10 Ma = 0.75、Re = 3×106，不同模型姿态角测量方法对大展弦比民机模型气动力系数曲线的影响
Figure 10. Variations of aerodynamic coefficients of a large aspect ratio civil aircraft model with the model attitude angle obtained by different measurement methods at Ma = 0.75 and Re = 3×106
![]()
图 11 天平初始载荷计算与修正的流程
Figure 11. Calibration and correction process of the initial balance load
![]()
图 12 不同滚转角范围线性回归结果对比
Figure 12. Comparison of linear regression results in different rolling angle ranges
![]()
图 13 Ma = 0.75、Re = 3×106，全局线性回归和局部线性回归的阻力系数曲线
Figure 13. Global and local linear regressions of drag coefficients at Ma = 0.75 and Re = 3×106
![]()
图 17 Ma = 0.75，未开启和开启前后置减振器的模型振动情况对比
Figure 17. Comparison of the model vibration without and with the anti-vibration system at Ma = 0.75
![]()
图 18 Ma = 0.75，减振器对降低升力随时间变化曲线振荡幅度的作用
Figure 18. Effect of the anti-vibration system on the temporal lift oscillation at Ma = 0.75
![]()
图 19 Ma = 0.75 减振器对拓展迎角范围的作用
Figure 19. Effect of anti-vibration system on the range ofattack angle
![]()
图 21 形变测量与CFD相结合的弹性变形修正计算流程
Figure 21. Elastic deformation correction process based on video measurement and CFD
![]()
图 23 ETW和AVIC的形变测量结果对比
Figure 23. Comparisons of bend and twsit deformations measured by ETW and AVIC
![]()
图 24 不同雷诺数下试验与CFD计算得到的升阻力系数差量对比曲线
Figure 24. Lift and drag coefficients obtained by experiments and CFD simulations at different Reynolds numbers
![]()
图 25 计算所得的民机模型弹性变形前后气动力与试验数据对比
Figure 25. Comparison of aerodynamic force coefficients before and after elastic deformation of a civil aircraft model between experimental and computational data
![]()
图 26 民机模型弯扭变形沿机翼展向分布
Figure 26. Distributions of the bending and twisting deformation along the spanwise direction of the wing of a civil aircraft model
![]()
图 27 Ma = 0.75、Re = 3×106，大展弦比民机模型在FL-62和ETW的升力系数曲线
Figure 27. Comparisons of lift coefficients of a large aspect ratio civil aircraft model measured by ETW and AVIC at Ma = 0.75 and Re = 3×106
![]()
图 28 Ma = 0.75、Re = 3×106，大展弦比民机模型在FL-62和ETW试验的阻力系数曲线
Figure 28. Comparisons of drag coefficients of a large aspect ratio civil aircraft model measured by ETW and AVIC at Ma = 0.75 and Re = 3×106
表 1 测力试验数据重复性精度国军标指标
Table 1 GJB criteria of the repeatability accuracy of force measurement data
阻力系数
均方根偏差\delta_{C_x}升力系数
均方根偏差\delta_{C_y}俯仰力矩系数
均方根偏差\delta_{C_{mz}}合格指标 0.0005 0.0020 0.0010 先进指标 0.0001 0.0008 0.0003 横向力系数
均方根偏差\delta_{C_z}滚转力矩系数
均方根偏差\delta_{C_{mx}}偏航力矩系数
均方根偏差\delta_{C_{my}}合格指标 0.00080 0.00020 0.00020 先进指标 0.00015 0.00005 0.00008 
下载: 导出CSV
表 2 2.4 m连续式跨声速风洞民机模型测力试验数据重复性精度（Re = 3×106）
Table 2 Repeatability accuracy of force measurement data of a civil aircraft model (Re = 3×106)
阻力系数
均方根偏差\delta_{C_x}升力系数
均方根偏差\delta_{C_y}俯仰力矩系数
均方根偏差\delta_{C_{mz}}合格指标 0.00050 0.00200 0.00100 先进指标 0.00010 0.00080 0.00030 Ma=0.5 0.00004 0.00030 0.00017 Ma=0.75 0.00002 0.00016 0.00015 Ma=0.8 0.00004 0.00033 0.00019 Ma=0.9 0.00009 0.00030 0.00017 横向力系数
均方根偏差\delta_{C_z}滚转力矩系数
均方根偏差\delta_{C_{mx}}偏航力矩系数
均方根偏差\delta_{C_{my}}合格指标 0.00080 0.00020 0.00020 先进指标 0.00015 0.00005 0.00008 Ma=0.5 0.00016 0.00001 0.00001 Ma=0.75 0.00017 0.00001 0.00001 Ma=0.8 0.00021 0.00002 0.00001 Ma=0.9 0.00027 0.00002 0.00002
下载: 导出CSV
-
[1] 崔晓春. 连续式跨声速风洞气动设计技术研究[D]. 北京: 北京航空航天大学, 2020. CUI X C. Research on aerodynamic design technology of continuous transonic wind tunnel[D]. Beijing: Beihang University, 2020.
[2] 王艳阳, 李小刚, 张明龙, 等 . 温度分布不均匀的天平阻力元零点温度效应补偿与修正技术研究[J]. 航空科学技术,2020 ,31 (12 ):26 −32 .WANG Y Y, LI X G, ZHANG M L, et al . Research on compensation and correction of zero temperature effect of axial force element of balance with uneven temperature distribution[J]. Aeronautical Science & Technology,2020 ,31 (12 ):26 −32 (in Chinese).[3] 李强, 崔智强, 李小刚, 等 . 天平零点温度效应补偿技术[J]. 弹箭与制导学报,2018 ,38 (3 ):119 −120,124 . doi: 10.15892/j.cnki.djzdxb.2018.03.029LI Q, CUI Z Q, LI X G, et al . Technology on zero temperature effect compensation in balance[J]. Journal of Projectiles, Rockets, Missiles and Guidance,2018 ,38 (3 ):119 −120,124 (in Chinese). doi: 10.15892/j.cnki.djzdxb.2018.03.029[4] 李纯, 李琦, 姚程炜, 等 . 应变天平零点温度漂移补偿研究[J]. 传感器世界,2016 ,22 (7 ):14 −17 .LI C, LI Q, YAO C W, et al . Study of temperature drift compensation in strain gauge balance[J]. Sensor World,2016 ,22 (7 ):14 −17 (in Chinese).[5] 刘高计, 谌满荣, 陶文革, 等 . 风洞实验应变天平温度效应线性修正法[J]. 弹箭与制导学报,1997 ,17 (4 ):58 −60 .LIU G J, CHEN M R, TAO W G, et al . Linear correction method for temperature effect of strain balance in wind tunnel experiment[J]. Journal of Projectiles, Rockets, Missiles and Guidance,1997 ,17 (4 ):58 −60 (in Chinese).[6] 杨洪胜, 米鹏, 向光伟 . 基于深低温物理场下低温天平阻力元件热应变分析[J]. 中国科技信息,2017 (22 ):89 −93 . doi: 10.3969/j.issn.1001-8972.2017.22.034YANG H S, MI P, XIANG G W . Thermal strain analysis of resistance element of cryogenic balance based on deep cryogenic physical field[J]. China Science and Technology Information,2017 (22 ):89 −93 (in Chinese). doi: 10.3969/j.issn.1001-8972.2017.22.034[7] HEREFORD J, PARKER P A, RHEW R D. TIGER: Development of thermal gradient compensational algorithms and techniques, 200400865533 [R]. Hampton, Virginia: NASA Technical Report, 2004.
[8] 贺德馨. 风洞天平[M]. 北京: 国防工业出版社, 2001: 1-9. HE D X. Wind tunnel balance[M]. Beijing: National Defense Industry Press, 2001: 1-9(in Chinese).
[9] 徐重玖. 风洞应变天平设计校准及灵敏度温度补偿[D]. 沈阳: 东北大学, 2015. XU C J. Design and calibration of strain gauge balance system in wind tunnel and temperature to sensitive compensation[D]. Shenyang: Northeastern University, 2015 (in Chinese).
[10] 苗磊, 马涛, 徐志伟, 等 . 热力耦合作用下的风洞应变天平校准技术[J]. 仪器仪表学报,2022 ,43 (3 ):153 −162 .MIAO L, MA T, XU Z W, et al . The calibration technology of wind tunnel strain-gage balance under the action of thermo-mechanical coupling[J]. Chinese Journal of Scientific Instrument,2022 ,43 (3 ):153 −162 (in Chinese).[11] FOSTER J M, ADCOCK J B. User’s Guide for the national transonic facility research data system, NASA-TM-110242[R]. Hampton, Virginia: NASA Technical Memorandum, 1996.
[12] 张刃, 张明龙, 杜文天. 风洞测力试验自重修正方法研究[C]// 第七届近代实验空气动力学会议论文集. 铜仁: 中国空气动力学会, 2019. [13] PARYZ R W. Recent developments at the NASA langley research center national transonic facility[C]// 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Orlando, Florida: AIAA, 2011.
[14] BOYET G . European strategic wind tunnels improved research potential program overview[J]. CEAS Aeronautical journal,2018 ,9 :249 −268 . doi: 10.1007/s13272-018-0305-4[15] 王娜, 李艳亮, 董军. 航空数值计算平台ENSMB简介[C]// 中国力学学会学术大会2009论文摘要集, 郑州: 中国力学学会, 2009: 344-345. [16] 王娜, 张铁军, 董军 . 多重网格技术在民机粘性流场数值模拟中的应用研究[J]. 气动研究与试验,2009 ,27 (2 ):5 −8 .[17] HEEG J, CHWALOWSKI P, FLORANCE J P, et al. Overview of the aeroelastic prediction workshop[C]// 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Texas: AIAA, 2013.
[18] CHWALOWSKI P, HEEG J, WIESEMAN C D, et al. FUN3D analyses in support of the first aeroelastic prediction workshop[C]// 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Texas: AIAA, 2013.
计量
- 文章访问数: 985
- HTML全文浏览量: 11
- PDF下载量: 36
