0.   引　言

在当今全球化高速发展大背景下，大型飞机作为长途旅行和货运的重要交通工具，其重要程度急剧增大^[1]。因此，研制大型飞机对推动国家科技进步和产业升级至关重要。但大型飞机尺寸大、飞行雷诺数高，给风洞试验和飞机的设计研发带来了极大挑战，由此引发的雷诺数效应问题成为大型飞机气动设计研发的关键问题，一直以来都是研究的热点和难点。

风洞尺寸和实际条件的限制使得风洞试验所采用的缩比模型尺寸远小于真实飞机，这将导致风洞试验雷诺数和飞行雷诺数之间存在差异，通常将这种由雷诺数差异所引起的附面层结构及飞机气动特性改变称为“雷诺数效应”。对大型飞机研制来说，由于风洞试验雷诺数过低所带来的问题尤为突出^[2]。现代大型亚声速运输机飞行雷诺数高达7000 ～ 8000万，而常规风洞试验雷诺数通常在百万量级，和实际飞行雷诺数相差一个数量级以上^[3-4]。这种雷诺数的差异通常会引起大型飞机机翼边界层发展/转捩、流动分离、激波/边界层干扰等复杂流动现象出现结构性改变，进而对飞机失速特性、摩擦阻力及激波特性产生影响，包括飞机的最大升力系数C_L,max、升力系数C_L、焦点位置、力矩拐点、激波位置等参数，严重影响飞机巡航升阻比等关键气动指标的精准度^[5-10]。当雷诺数差异所引起的飞机气动力/力矩等关键指标偏差难以靠飞机各舵面最初的设计极限能力补足，且在实际飞行试验尤其是在接近飞行包线时，可能会导致飞机失控甚至坠机等灾难性后果。综上，雷诺数效应会影响飞机的飞行安全和飞行性能，延缓飞机研发进度，增加研发成本，是大型飞机研发的关键技术难题。

本文针对大飞机研制面临的雷诺数效应问题，重点关注雷诺数效应的影响机制和研究进展，首先引入大型飞机雷诺数效应的两种常用研究手段，然后从高速气动设计和低速设计两个方面分别介绍了雷诺数效应在设计中的影响研究，接着介绍与雷诺数效应相关的流动机理研究，并综述了雷诺数效应问题的具体解决方法，最后给出了相关结论和展望。

1.   大型飞机雷诺数效应研究手段

1.1   风洞试验

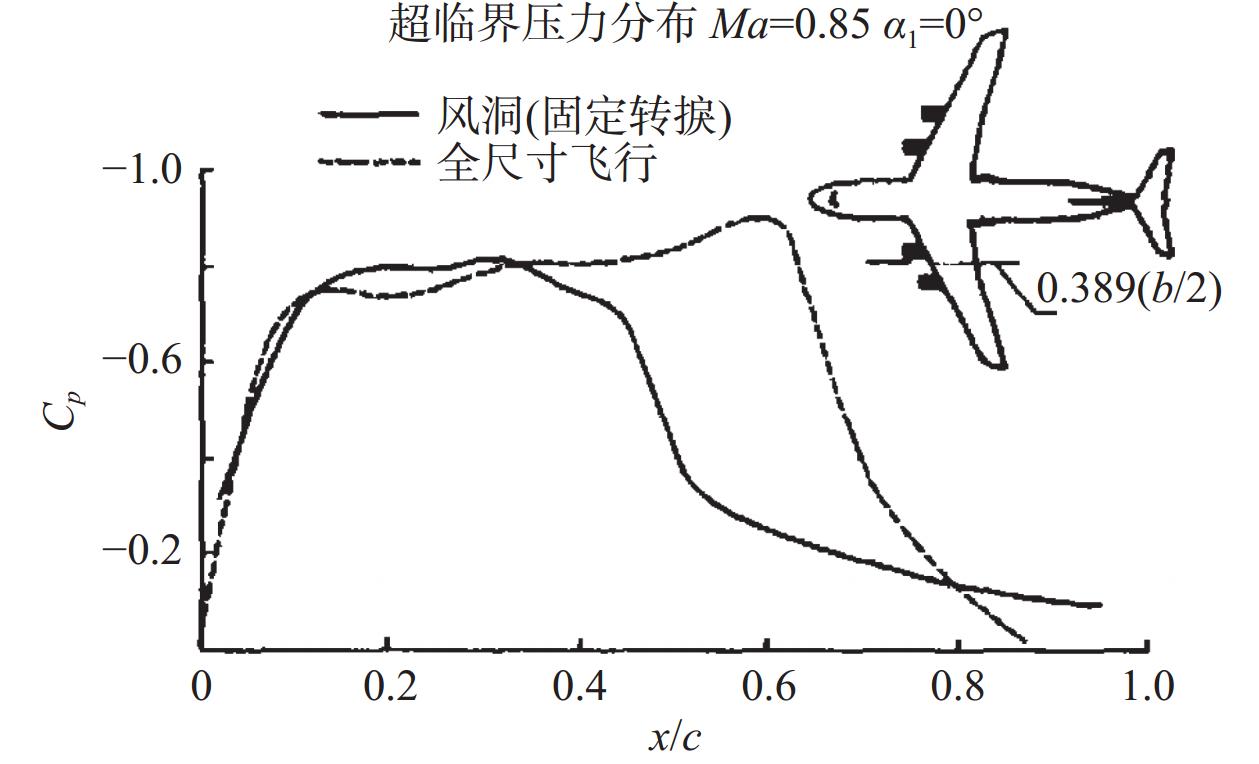
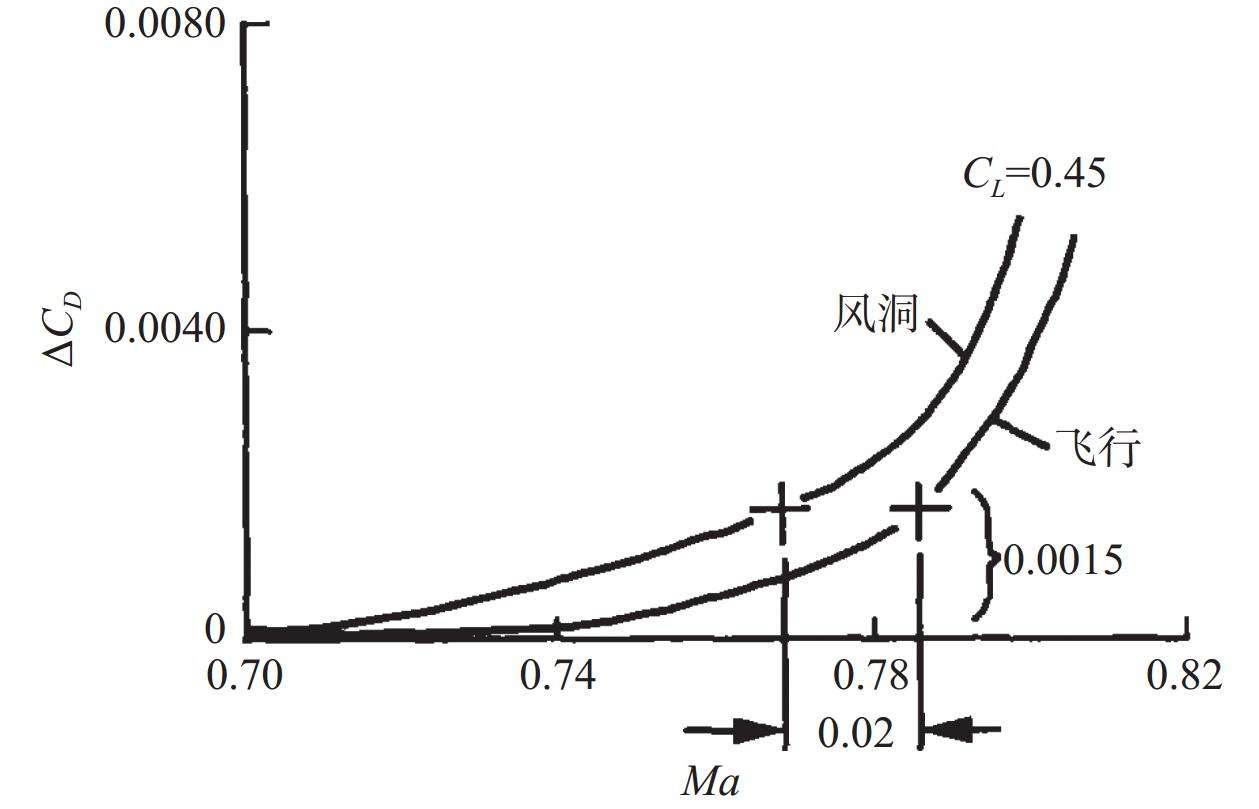
美国在大型飞机的设计研发过程中，最早系统深入地开展了雷诺数效应影响研究，他们在研发C-5A和C-141飞机时，发现雷诺数对飞机的阻力发散和压力分布都会产生很大的影响。图1为 C-5A飞机阻力发散马赫数的风洞试验值与飞行值，可以看出，由于雷诺数的影响，C-5A大型运输类飞机风洞试验雷诺数下的阻力发散马赫数比飞行试验提前了0.02，为了弥补该偏差，研究人员需额外耗费大量时间和经费去矫正^[6]。图2所示为C-141飞机机翼中部剖面风洞试验和飞行试验压力分布， 可见，C-141运输机在风洞试验和飞行试验下，超临界机翼中部剖面弦向压力分布差异巨大，激波位置相差近20%弦长^[6-7]，导致焦点位置出现重大偏差，险些出现机毁人亡的重大事故^[6]。因此，把握大空域宽速域下雷诺数变化对气动特性的影响规律是飞行器精细化设计的前提。为了突破雷诺数对大型飞机研发的限制，美国建立了一大批大尺寸风洞群，最大试验段尺寸高达80 foot × 120 foot，同时利用低温增压测试技术提高测试雷诺数，支撑了大型飞机的设计研发。

图  1  C-5A飞机阻力发散马赫数风洞试验值与飞行值比较^[6]

Figure  1.  Comparison of drag divergence Mach number of C-5A airplane obtained by wind tunnel and flight tests^[6]

下载: 全尺寸图片 幻灯片

图  2  C-141飞机机翼中部剖面风洞和飞行试验压力分布^[7]

Figure  2.  Surface pressure distributions in the midspan of C-141 aircraft wing obtained by wind tunnel and flight tests^[7]

下载: 全尺寸图片 幻灯片

欧洲空客A380作为当前最大的民用客机^[11]，飞行雷诺数极高。为开展从高速巡航特性的评估分析到低速增升装置系统的设计（图3），研究人员结合一系列不同雷诺数风洞试验数据和高可信度计算流体力学（Computational Fluid Dynamics, CFD）技术开展了雷诺数修正和外推，从构型设计到最终的数据验证，花费了大量时间和成本，最终才达到飞行雷诺数要求。

图  3  A380飞机半模高升力系统试验^[11]

Figure  3.  High lift system test of a A380 aircraft half model^[11]

下载: 全尺寸图片 幻灯片

除了常规布局飞机，以翼身融合体为代表的新型气动布局逐渐成为下一代大型运输类飞机的理想构型。对于这类非常规布局飞行器，雷诺数的影响比传统布局更加值得关注，这是由于新的布局对低速起降的要求更加严苛，高速巡航状态的设计指标更高，同时由于融合布局纵向稳定性较差，升降舵操纵效率更低，因此雷诺数的影响会直接影响飞机的飞行安全，需要更加重视。典型代表是X-47飞机（图4），其研发过程需要丰富的数据和理论支撑^[12]。

图  4  非常规布局风洞试验^[12]

Figure  4.  Wind tunnel test of unconventional layout^[12]

下载: 全尺寸图片 幻灯片

为了减小雷诺数导致的试验数据误差，需要深入开展雷诺数效应影响研究，总结规律探究机理，对风洞试验结果进行修正，以逼近真实飞行条件，提升试验数据可信度^[13]。为此，各航空大国也相继建设了高雷诺数风洞，如德国宇航研究院的KKK风洞、美国的NTF（National Transonic Facility）风洞^[14]、欧洲的ETW（European Transonic Windtunnel）风洞^[15]等，通过这些风洞获得了大量的宝贵试验数据，为推动雷诺数效应研究做出了巨大贡献。

美国在20世纪60年代末和70年代初曾针对Learjet模型开展了小尺度和全尺度模型风洞试验以及自由飞行测试条件下全机气动特性研究^[16]，结果表明雷诺数效应对全机气动特性有巨大影响。国内也有学者利用风洞开展了相关研究，Wang等^[17]通过试验研究雷诺数对RAE 2822翼型气动特性的影响，孙智伟等^[18]在某NF-3和NF-6风洞中进行超临界翼型的设计和试验研究，得出了超临界翼型在高、低速时的分离演化特性等。

1.2   数值模拟

风洞试验费用高昂，其试验测试能力等限制了雷诺数效应研究，而越来越多的研究人员开始使用数值模拟技术。Pettersson等^[19]、Crippa等^[20]、Wilkending等^[21]、Nangia等^[22]先后利用数值模拟开展了雷诺数差异对运输机、三角翼、后掠翼等构型流场和气动特性的影响研究。结果表明，雷诺数的变化对升阻力、俯仰力矩以及分离涡特性会产生显著影响，这种差异表征为雷诺数的非线性函数，并且指出发展更高精度的CFD方法将显著提高风洞结果对自由飞行的预测能力。

国内的张培红等^[23]、张辉等^[24]、张耀冰等^[25]、李忠武等^[26]、周林等^[27]、马明生等^[28]、张彦军^[29]也采用数值模拟方法研究雷诺数差异对运输机、小展弦比飞翼、增升装置、翼/身组合体等构型气动性能的影响，并尝试给出相应修正措施。

整体而言，随着雷诺数增加，附面层厚度减小，激波及流动分离位置后移，从而导致后部载荷增大，使得升力系数和低头力矩呈现增大趋势，阻力系数呈现减小趋势。

具体来看，雷诺数对气动特性的影响与外形息息相关。对翼型/机翼而言，厚度和弯度是决定雷诺数影响的重要参数，增加翼型/机翼厚度和弯度，雷诺数对升阻特性和力矩特性的影响会增大，同样地，雷诺数对运输类飞机气动特性的影响较为复杂。对机身而言，后体收缩及上翘角则是造成雷诺数影响规律与机翼不同的主要因素。此外，不同外形的自准区雷诺数也有差别，并且与攻角和马赫数相关，使得学者们大多给出定性结论，难以总结出定量规律。

在更深入的研究中，冯涛等^[30对典型气动负载涡轮叶片在不同雷诺数下边界层特性变化进行敏感性研究，靳允立等^[31]采用不同湍流模型研究翼型失速及风速变化引起的雷诺数改变对翼型和风力机气动性能的影响。

2.   高速巡航状态的雷诺数效应研究

本节以大型运输类飞机高速气动设计的需求为出发点，针对其高亚声速小攻角定升力巡航特点（马赫数为0.6 ～ 0.8），详细地阐述了超临界翼型机翼设计和全机气动力设计中的雷诺数问题，并总结分析了雷诺数的影响规律。

2.1   超临界翼型/机翼的雷诺数问题

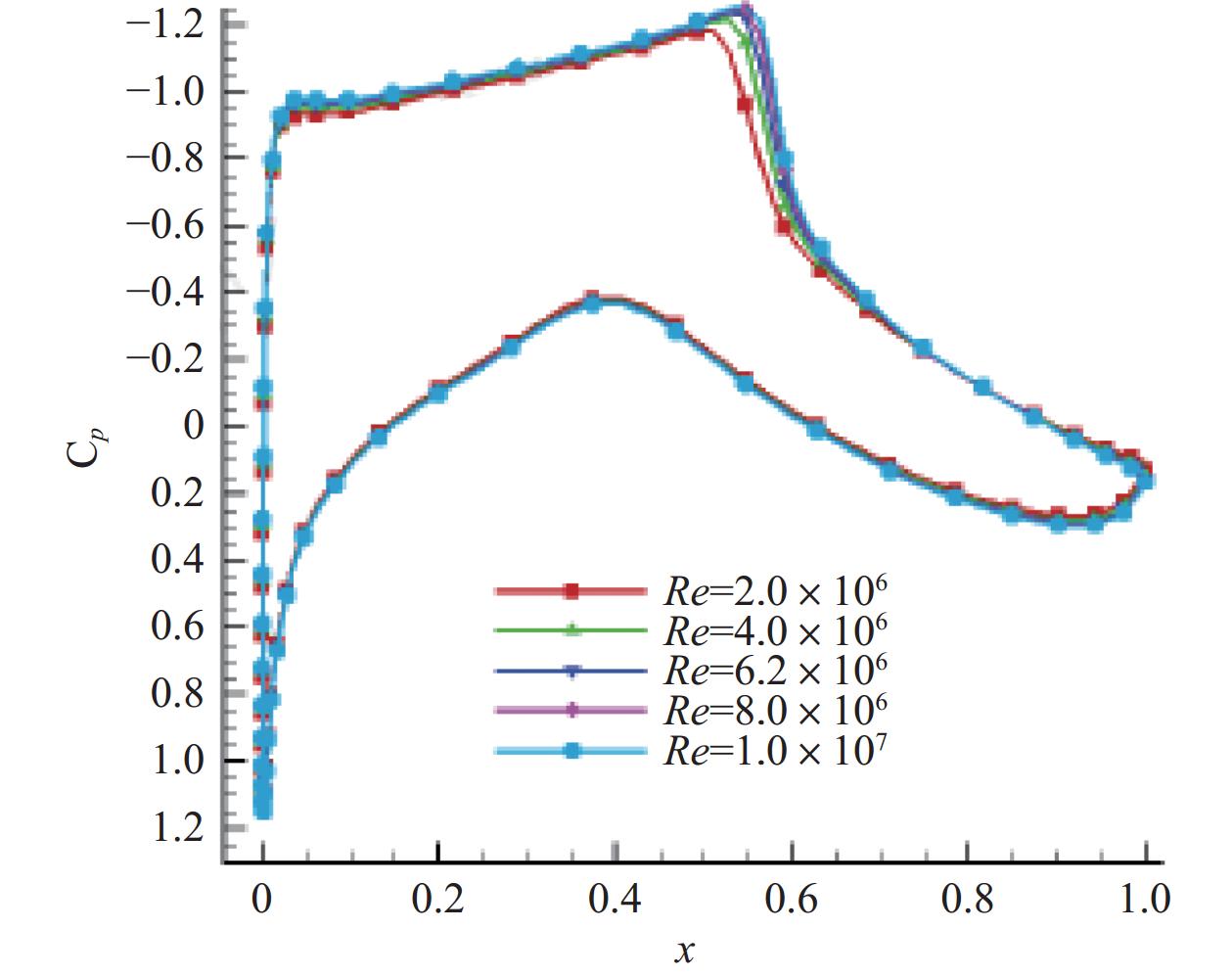
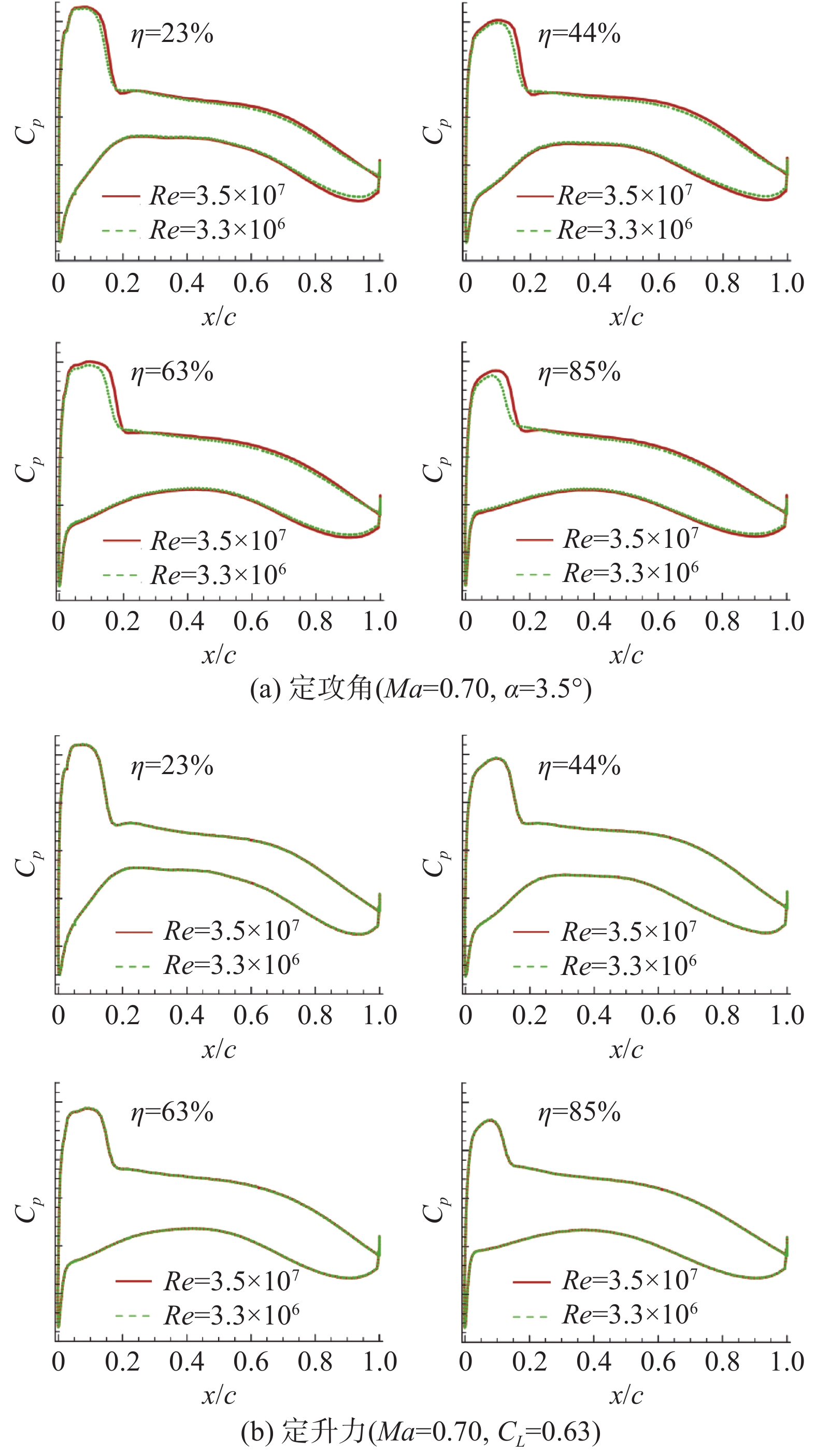
为了满足大型运输类飞机在高速巡航阶段的气动效率要求，目前，国内外较为成熟的气动布局设计中均采用超临界翼型，可有效提高阻力发散马赫数和升阻比。但该类翼型气动特性对雷诺数变化非常敏感，随着边界层发展的累积，翼型表面压力分布也会呈现出渐进的变化趋势。以RAE 2822超临界翼型为例，采用CFD进行数值计算，保持马赫数$Ma = 0.75$、迎角$\alpha = 2.72^\circ$不变，改变雷诺数分析该翼型高亚声速下气动特性的变化情况。如图5所示，随着雷诺数增大，黏性效应减小，附面层变薄，波前负压增大；激波位置随着雷诺数的增大而后移，强度随雷诺数增大而增强，激波附面层干扰加剧，使得激波后附面层内更易分离。

图  5  雷诺数对超临界翼型压力分布影响^[32]

Figure  5.  Reynolds number effects on pressure distribution of supercritical airfoils^[32]

下载: 全尺寸图片 幻灯片

类似地，文献[29]针对某超临界机翼所开展的研究中，给出了不同雷诺数下机翼剖面压力分布的对比，如图6所示。在固定攻角和来流马赫数条件下，增大雷诺数会使得机翼不同展向位置剖面的压力分布形态呈现出一致的变化趋势，激波位置后移，激波强度也略微增强，上表面负压增大，下表面尤其是接近后缘位置处压力也略微增大；在固定升力系数和来流马赫数下，增大雷诺数对机翼不同展向位置剖面的压力分布影响不大，曲线基本重合。这表明，采用不同的计算试验策略（定攻角或定升力）会对雷诺数影响偏差产生区别，若针对该构型采用定升力条件试验可知，小雷诺数风洞测压结果与实际飞行基本一致。该结论可进一步进行数值和试验验证，并应用到大型运输类飞机设计研发中。

图  6  不同雷诺数下某超临界机翼剖面压力分布对比^[29]

Figure  6.  Pressure distributions of a supercritical wing at different Reynolds numbers^[29]

下载: 全尺寸图片 幻灯片

通过以上分析可知，雷诺数效应影响了超临界机翼的压力分布，从而影响了飞机的气动性能和边界特性。因此，在开展翼型和机翼试验时需要高度重视雷诺数效应问题，需开展雷诺数的影响规律研究，从而保证在设计点和边界状态的压力分布形态和性能指标。

2.2   全机气动特性的雷诺数影响

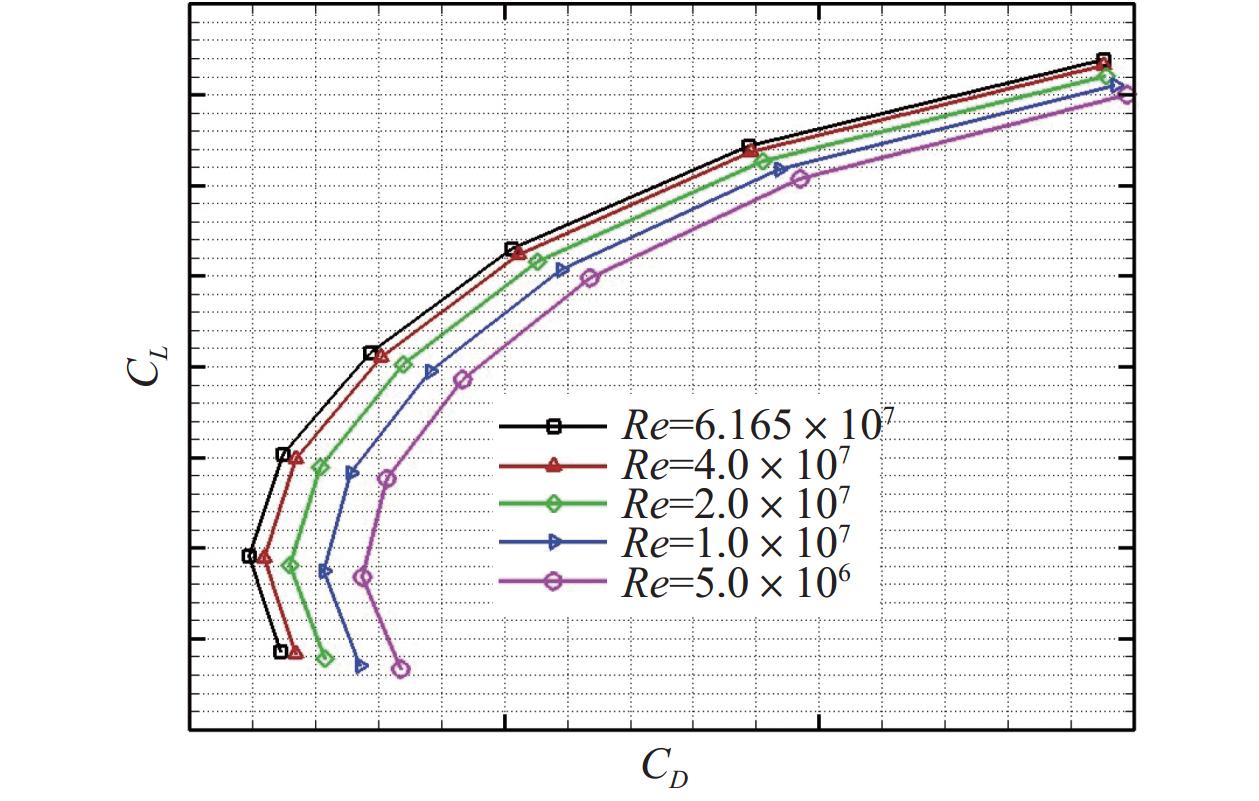
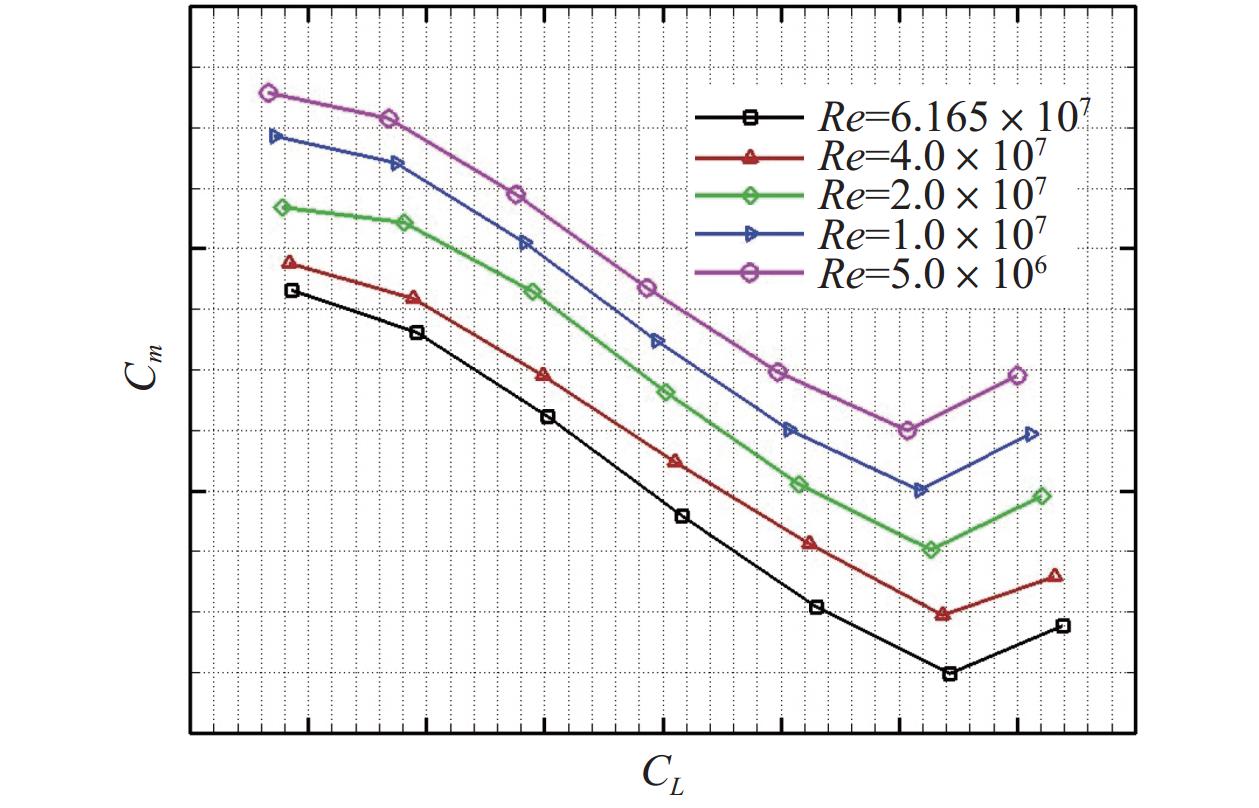
雷诺数对高亚声速巡航阶段的全机气动特性也会产生显著影响，尤其对是阻力特性及力矩特性的影响最大。通过对某大型运输类飞机开展整机气动特性数值模拟评估，如图7和图8所示，在相同升力系数下，随着雷诺数增大，阻力系数持续减小，俯仰力矩变大。这是因为雷诺数变化使得全机黏性效应减小，摩擦阻力减小，进而引起总阻力减小，全机升阻比增大。此外，雷诺数变化使得激波位置后移，翼型后加载更大，低头力矩也相应增大，这个现象在大型运输类飞机气动设计中需要格外重视。

图  7  雷诺数对极曲线的影响(CFD数值模拟结果)

Figure  7.  Reynolds number effects on the polar curve (CFD simulation results)

下载: 全尺寸图片 幻灯片

图  8  雷诺数对俯仰力矩的影响(CFD数值模拟结果)

Figure  8.  Reynolds number effects on pitching moment (CFD simulation results)

下载: 全尺寸图片 幻灯片

类似地，文献[9]针对某层流机翼验证机的研究也得出了一致的结论：这种呈现高度一致性的雷诺数影响规律是由于所采用的试验雷诺数尚未完全进入“自准区”^[32]范围，且风洞试验与数值模拟结果在大部分情况下吻合良好，因此可以充分利用变雷诺数CFD计算数据辅助风洞试验数据修正。文献[13]指出，对于高亚声速巡航状态下试验数据的雷诺数效应修正，可重点集中在对升力系数、阻力系数以及俯仰力矩系数等纵向气动数据的分析上。

3.   低速起降状态的雷诺数效应研究

除了高速巡航阶段，飞机低速起降阶段的高雷诺数问题也尤为重要。大型飞机在低速起降状态下，通常是大迎角小速度状态（马赫数：0.2 ～ 0.3，迎角：–4° ～ 20°），飞行雷诺数和试验雷诺数的差异主要影响的是最大升力系数以及失速形态，这两方面直接决定了飞机的起降性能和安全性能。

3.1   翼型/机翼的雷诺数效应研究

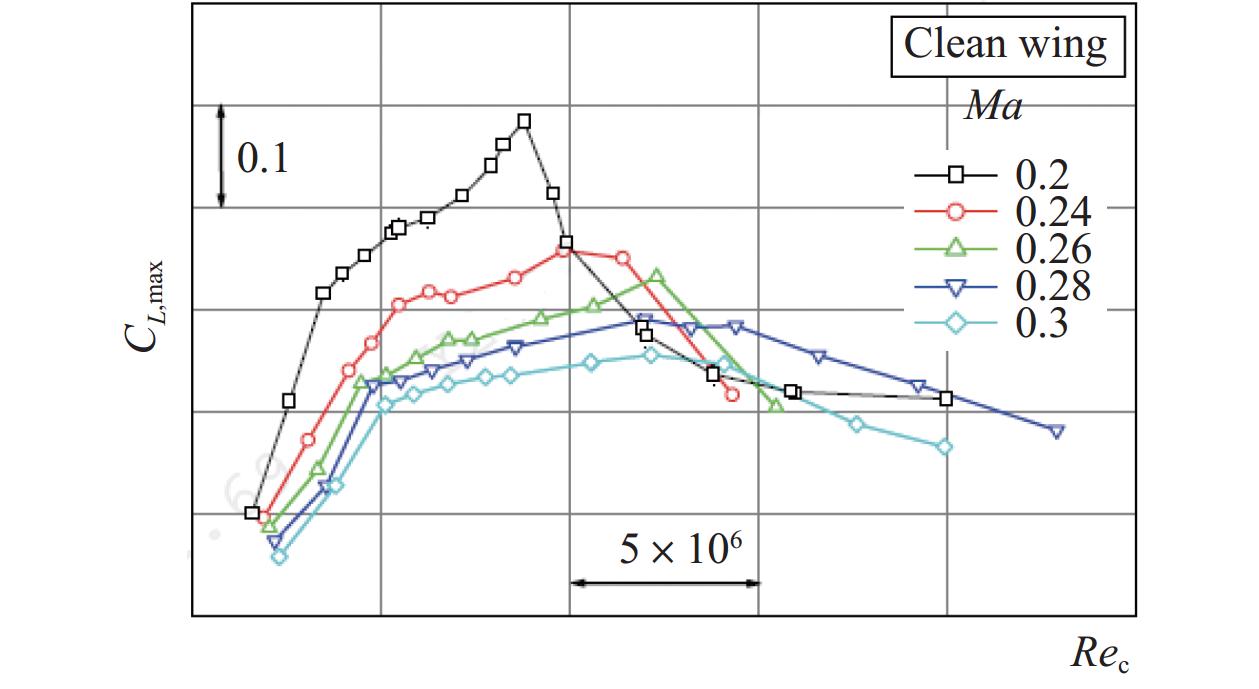
低速高升力下的流动现象与雷诺数密切相关，能否实现真实飞行雷诺数的模拟逐渐受到各飞机设计单位的重视。例如针对某干净机翼的低马赫数最大升力系数研究中，根据ETW风洞试验结果^[33]（图9），观察到随着雷诺数增大，最大升力系数C_L,max出现陡降，变化呈现非线性趋势，这为分析和预测带来了很大风险和不确定性。因此，针对雷诺数对低速最大升力系数影响的问题，设计人员需要结合风洞试验和高可信度数值模拟技术进行系统和深入地研究，明确雷诺数对起降失速附近流场和气动特性的影响规律。

图  9  典型雷诺数对最大升力的影响(ETW风洞试验结果)

Figure  9.  Reynolds number effects on maximum lift (ETW test results)

下载: 全尺寸图片 幻灯片

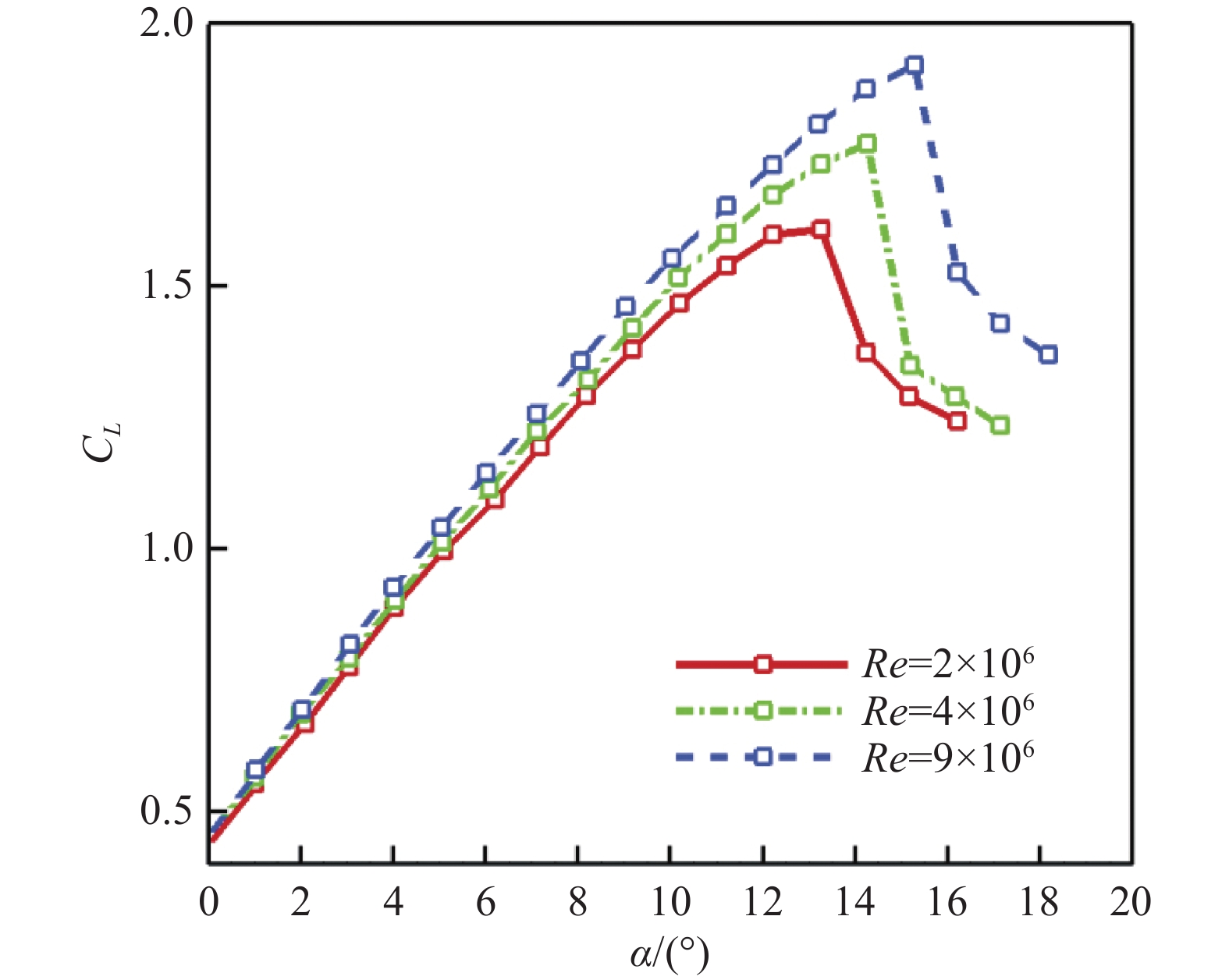
文献[34]中，研究人员采用数值模拟方法对某翼型边界层发展及失速特性开展了更细致研究，探究雷诺数变化对飞机尤其是翼型失速问题的空气动力学机理。首先研究了不同雷诺数下的升力曲线，如图10所示，可见随着雷诺数增大，翼型的失速迎角和最大升力系数也随之变大。为了分析雷诺数的影响机理，进一步研究了流场细节^[34]。研究表明，导致雷诺数对翼型最大升力系数和升力斜率影响的一个主要机制是转捩，由图11可见，不同雷诺数下翼型转捩位置和形态截然不同，随着雷诺数增加，转捩位置前移，转捩形态也明显不同，这一点在图12的压力分布上也有明显体现，转捩位置和形态的不同直接导致升力线斜率和失速形态的不同。

图  10  不同雷诺数下翼型升力系数随迎角变化图^[34]

Figure  10.  Variations of lift coefficient with the angle of attack at different Reynolds numbers ^[34]

下载: 全尺寸图片 幻灯片

图  11  翼型表面摩擦系数分布^[34]

Figure  11.  Airfoil surface friction coefficient distribution^[34]

下载: 全尺寸图片 幻灯片

图  12  翼型表面压力分布对比^[34]

Figure  12.  Comparison of airfoil surface pressure distributions^[34]

下载: 全尺寸图片 幻灯片

3.2   低速增升装置的雷诺数效应研究

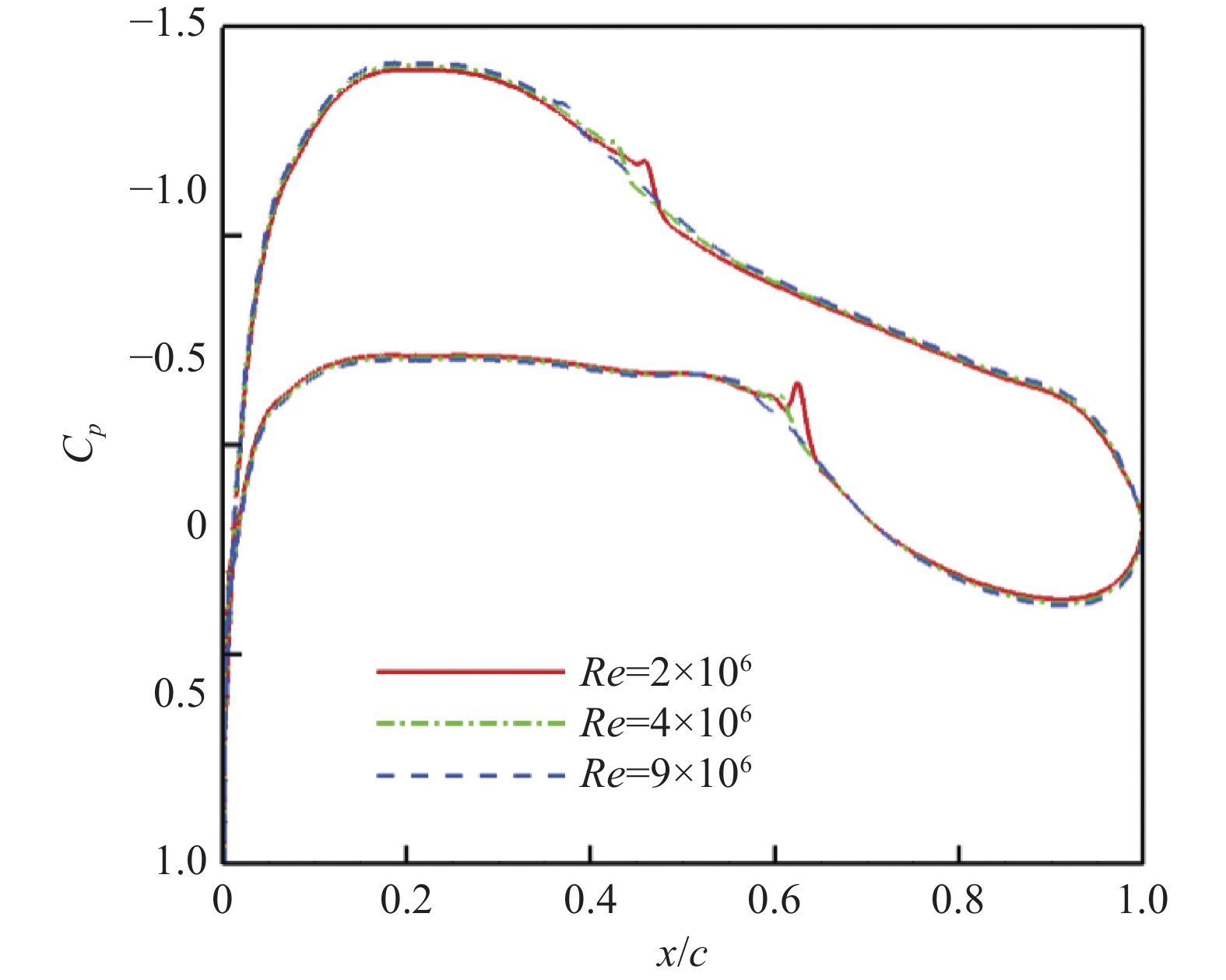
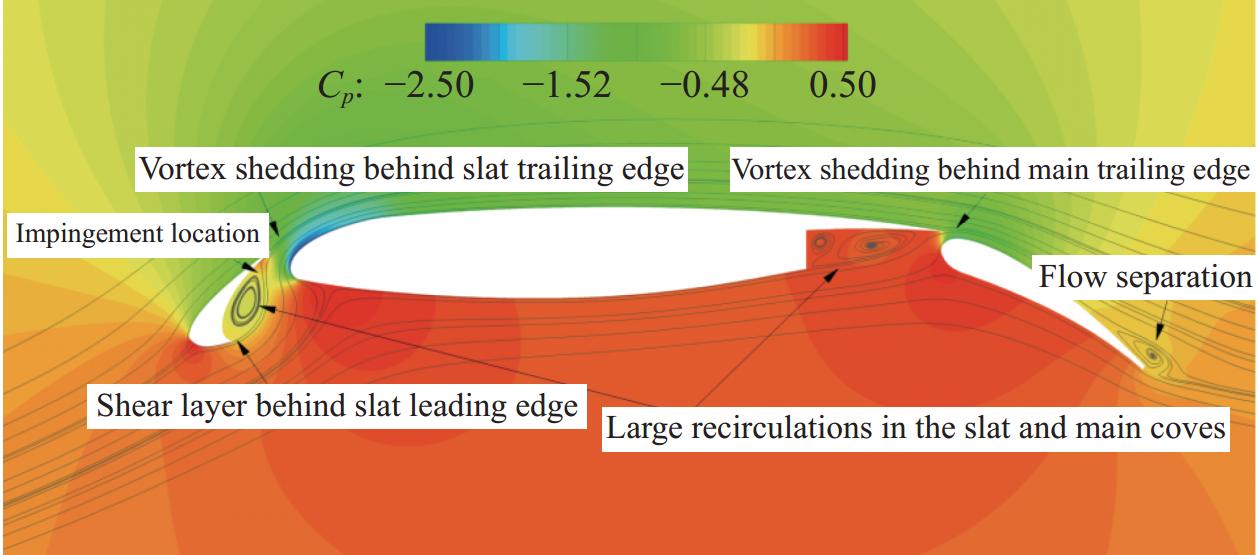
为了提升大型运输类飞机的起降性能和安全边界，除了提高翼型/机翼本身的最大升力系数和失速迎角外，设计低速增升装置也是飞机设计开发不可或缺的部分。低速增升装置作为一个多元复杂系统（图13），其各个部件相互干扰，同时伴随着缝道射流、尾流叠加干扰、边界层转捩和流动分离等复杂的黏性流动现象^[35]，如图14所示。对于这种复杂流动的模拟和分析，是当前CFD数值模拟的瓶颈和难题，通常需要采用风洞试验进行设计、分析和验证。由于风洞尺寸限制，试验雷诺数与实际飞行雷诺数存在差异，使得精确预测最大升力系数存在较大困难。雷诺数效应使得低速增升装置打开情况下的流场变得更加复杂^[36]。因此在大型运输类飞机增升装置设计分析时，需要开展增压和大尺寸风洞试验，同时借助高可信度数值模拟进行修正，尽量满足飞行状态的需求。

图  13  大型运输机的增升装置

Figure  13.  Lift-enhancing devices for large transport aircraft

下载: 全尺寸图片 幻灯片

图  14  增升装置流动的复杂性

Figure  14.  Typical flow fields around a lift-enhancing device

下载: 全尺寸图片 幻灯片

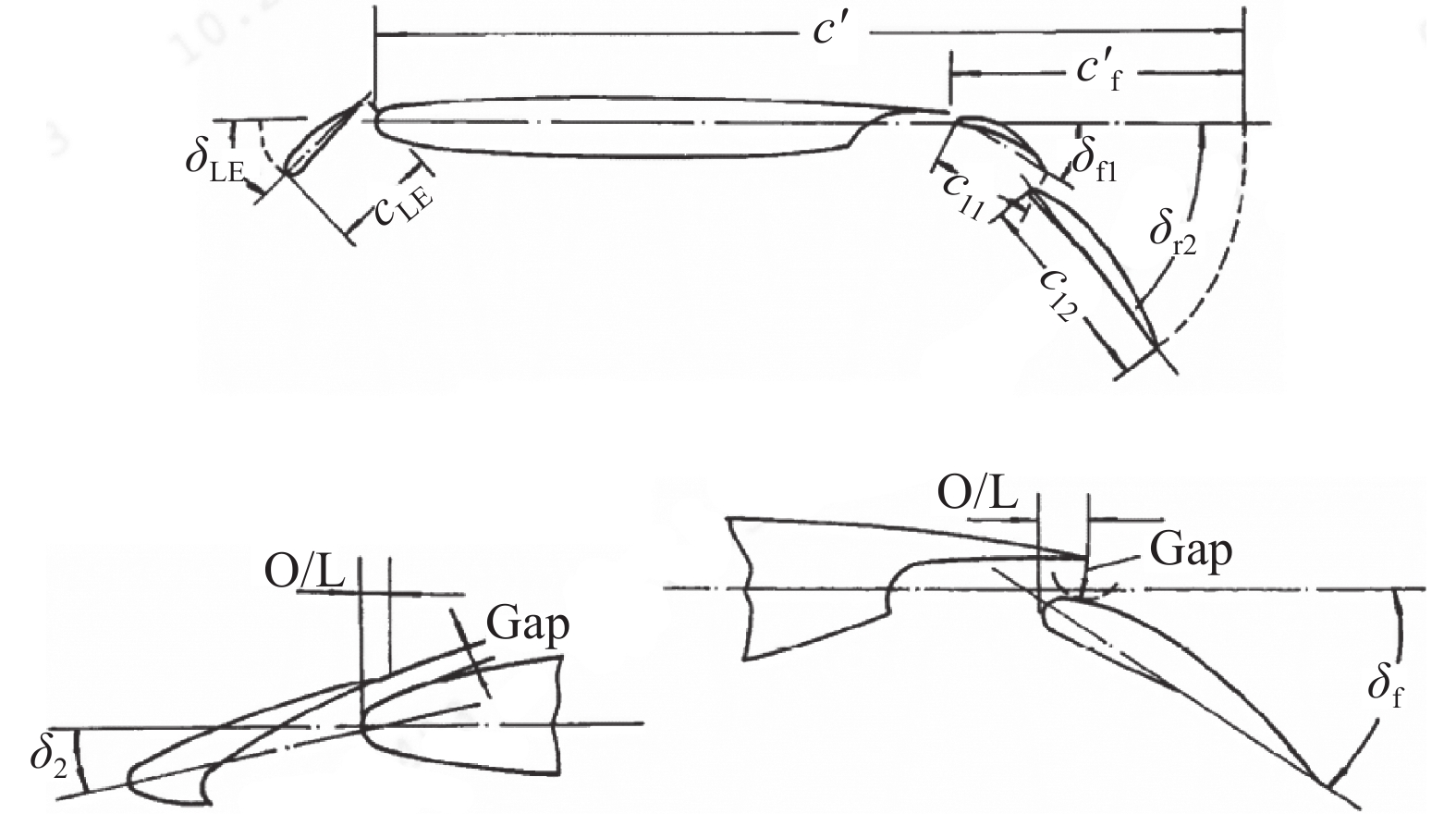
低速增升装置的设计关键之一是缝道参数设计，如图15所示。由于风洞试验模型缩比过程中的实际尺度效应，使得低速增升装置中的缝道难以与其他部件一样等比缩小，这是由于缝道内部的边界层不会缩小，当考虑扣除边界层厚度后的有效缝道参数时，便与真实缝道有所差异，而雷诺数对边界层的影响使得该差异变得更加难以量化，此时通过风洞试验获得的最优缝道参数难以保证在真实飞行条件下的设计性能，仍需进一步研究验证。

图  15  增升装置设计中的关键（缝道参数）

Figure  15.  Key parameters of lift-enhancing devices

下载: 全尺寸图片 幻灯片

NASA专门针对增升装置开展了系统的雷诺数影响研究^[37]，分别研究了二维多段翼型雷诺数效应及三维增升装置雷诺数效应。对于二维多段翼型，随着构型的不同，雷诺数效应也不尽相同，比如带前缘缝翼和不带前缘缝翼，雷诺数变化对流场及升力曲线的影响完全不同。对于简单襟翼构型，雷诺数增加会使最大升力系数增加，延缓流动分离；而对于带缝翼构型，雷诺数增加会通过附面层的变化改变缝隙效应，从而影响后翼的压力分布及混合边界层发展，在小攻角时会出现雷诺数增加、升力减小的反常现象。对于二维构型，雷诺数变化还会引起流动类型不同，如层流、转捩及分离泡等，进一步增加了雷诺数效应的复杂性。对于三维增升构型，雷诺数变化会导致附着线位置变化，在雷诺数很大的情况下将会出现层流区域以及再层流化等现象，层流和转捩的变化导致混合边界层及流动分离的变化，使得三维情况异常复杂。这些复杂的流动使增升装置的最大升力随雷诺数变化呈现非单调变化趋势。

欧盟为了进一步提升大型飞机增升装置的设计能力和高雷诺数测试水平，设立了EUROLIFT项目，以空客A380飞机增升装置为研究对象，依托ETW风洞，结合高可信度CFD技术，研究了雷诺数对增升装置流场和气动特性的影响，包括不同雷诺数下缝道参数、偏转角度的变化规律，并结合CFD技术进行了相关机理分析^[38]。

3.3   翼梢小翼的雷诺数效应研究

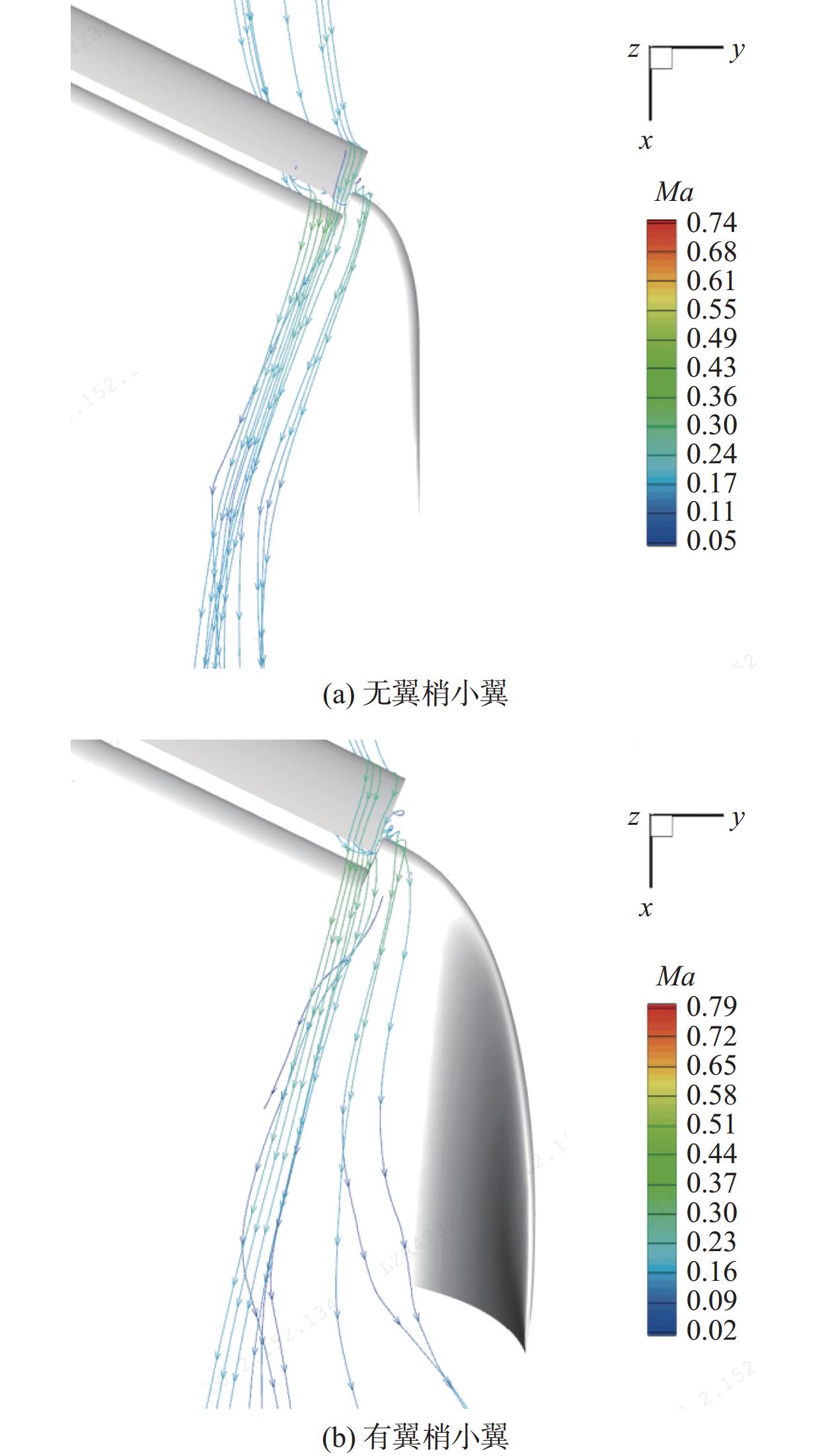
翼梢小翼是减小飞机诱导阻力，提升飞机飞行性能的重要部件。然而，翼梢小翼在低速起降状态下对飞机的操稳特性有很大的影响，例如，在起降阶段，翼梢小翼引起纵向稳定性降低，对于纵向稳定性要求较高的飞机，可能会影响其飞行安全。主要原因是增升装置打开后，缝翼与主翼之间存在剪刀口，部分气流会从剪刀口处溢出，形成一个空间涡系，造成副翼区更容易产生分离。这种复杂的流场细节给CFD数值模拟带来了极大的挑战（图16），通常需要借助风洞试验进行研究和分析，但是复杂的涡系结构和分离流动对雷诺数变化非常敏感，常规的风洞试验（Re ≈ 3000万）不能给出可靠的数据和涡系结构，导致翼梢小翼在大型运输类飞机设计中存在很大的不确定性，严重地制约了翼梢小翼的应用。

图  16  有/无翼梢小翼飞机的流场对比

Figure  16.  Flow fields around winglet airplanes with/without wingtips

下载: 全尺寸图片 幻灯片

3.4   涡流发生器的雷诺数效应研究

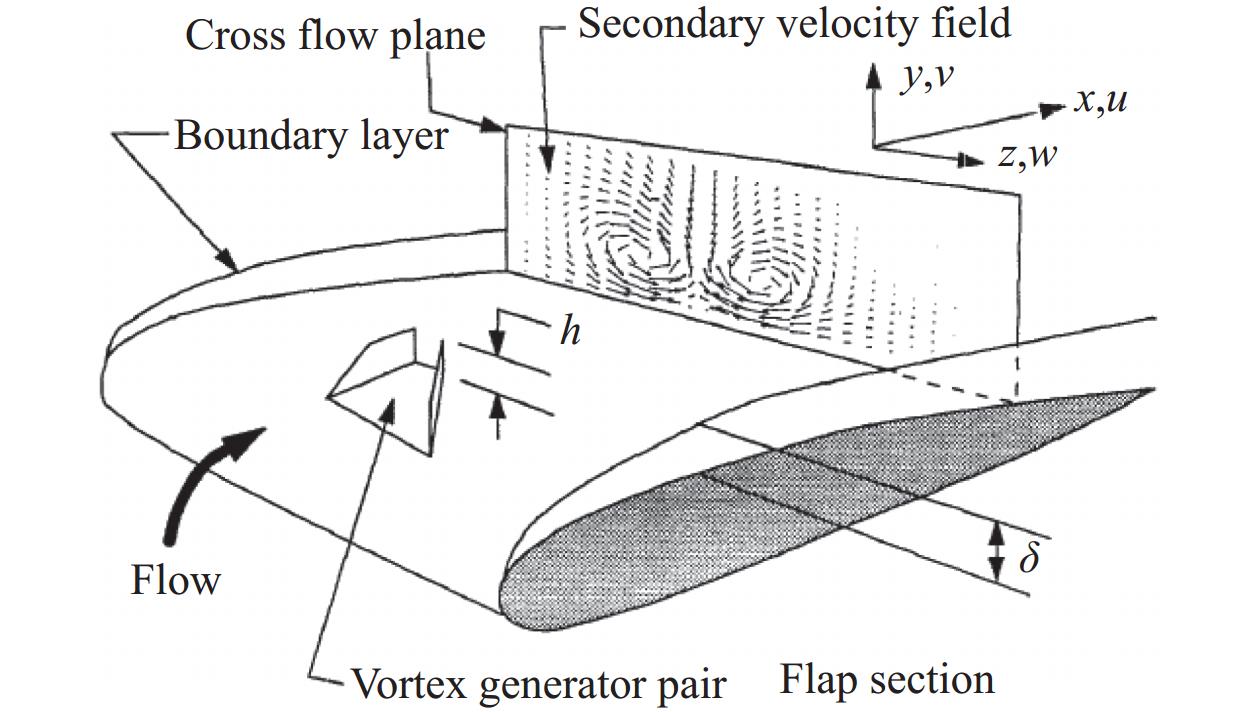
涡流发生器作为一种附面层分离的被动控制技术，自Taylor等^[39]首次提出这个概念后，被广泛应用于翼型/机翼增升^[40-43]、强化传热^[44-45]、进气道畸变控制^[46]等方面，其尺寸较小，且大多安装在黏性起主要作用的边界层内，构型和原理示意图如图17和图18所示。

图  17  大型飞机机翼上的涡流发生器阵列

Figure  17.  Vortex generator arrays on large airplane wings

下载: 全尺寸图片 幻灯片

图  18  涡流发生器原理示意图

Figure  18.  Schematic diagram of vortex generator

下载: 全尺寸图片 幻灯片

在涡流发生器作用下，大型飞机机翼在失速迎角后能够形成一个升力几乎不随迎角变化的相对稳定的高升力状态，并通过涡流发生器产生一系列的小涡，对附面层底部进行能量补充，抑制了失速流动的发生，从而增大失速迎角，并使得阻力大幅下降^[47]。这其中，雷诺数的差异会导致附面层厚度产生变化，当涡流发生器高度超过附面层高度时，破坏了流动本身，涡流发生器的被动失速流动控制效果便会快速失效^[9]。雷诺数效应作为涡流发生器设计和验证的关键因素之一，其抑制失速的效果需开展高雷诺数风洞试验及真实雷诺数飞行试验来验证。

4.   雷诺数效应的流动机理研究

由于大型飞机高雷诺数流场数值模拟及试验的难度较大，目前针对其雷诺数效应具体的流动机理研究尚停留在简单外形上，如旋成体、二维翼型等。

4.1   旋成体非对称涡绕流

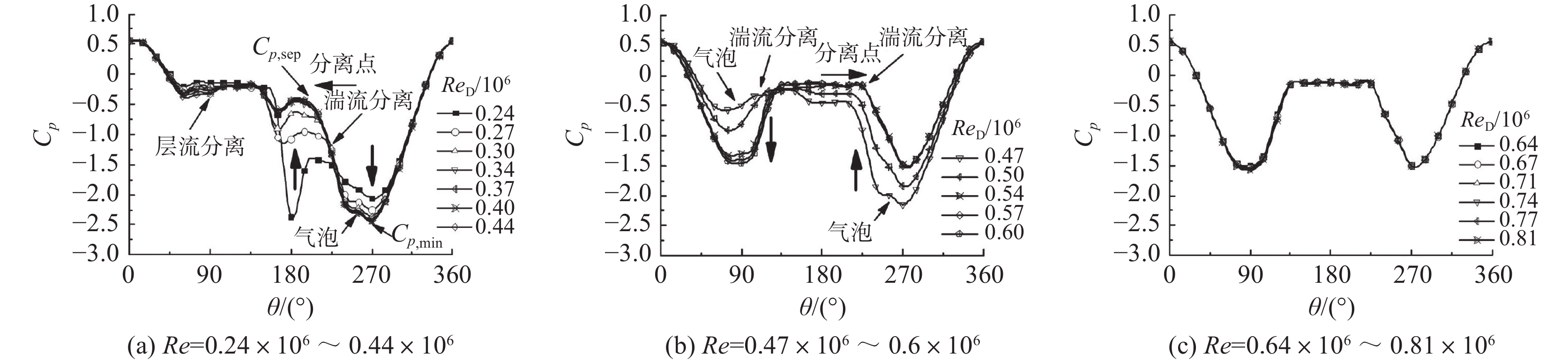
张彦军等^[34]、柏楠等^[48]采用试验手段对旋成体前体非对称涡流动临界雷诺数范围内的雷诺数效应开展了研究，如图19、图20所示。从图19（a）可见，随着雷诺数增加，转捩分离流型不断发展，其中速度最大点的压力${C_{p,\min }}$逐渐减小，分离点压力${C_{p,{\text{sep}}}}$逐渐增加，压力恢复$\Delta {C_p}$也逐渐增加（$\Delta {C_p} = {C_{p,{\text{sep}}}}- {C_{p,\min }}$），分离点逐渐向背风对称面移动并且由低位涡诱导的吸力峰值逐渐消失。从图20（a）中可观察到旋成体两侧分离形态不同，高涡侧只存在一条层流分离线，而低涡侧有明显的层流分离线、再附线以及湍流分离线，再附线和层流分离线的距离就是气泡的宽度，其中放大图为x/D = 3.35截面的气泡，表现在压力分布上即为流动经过速度最大点后在恢复过程中出现的一个小拐折，此区域称为临界雷诺数的起始发展区。

图  19  C_p ～ θ曲线（x/D = 3.35,$\gamma$ = 330^o）^[48]

Figure  19.  Variations of ${C_p}$ with θ at different Reynolds numbers ( x/D = 3.35,$\gamma$ = 330^o) ^[48]

下载: 全尺寸图片 幻灯片

图  20  油流结果^[48]

Figure  20.  Oil flow results^[48]

下载: 全尺寸图片 幻灯片

从图19（b）可以观察到，随着雷诺数继续增加，低位涡和高位涡两侧${C_{p,\min }}$分别增加和减小，分离点位置分别向迎风侧方向和背风侧移动，曲线左右逐渐趋于对称。从图20（b）可观察到高位涡开始出现湍流分离线，并且此湍流分离线刚刚从后体发展到前体。随着雷诺数继续增加，图19（c）中间两侧几乎呈现对称的压力分布形式，从图20（c）也可观察到此时两侧的转捩分离都发展得比较充分，分离线也比较对称，这一区域成为临界雷诺数区。

可见，旋成体左右两侧边界层类型的不同体现出了旋成体大迎角扰流的非对称性，并依此将临界雷诺数区域划分为临界起始发展区和临界区，从而总结出截面压力分布随雷诺数变化的演化规律。通过对该前体非对称涡扰流流动的研究，有助于对飞机在大迎角甚至过失速飞行时前体绕流复杂非对称涡流动现象机理的分析，从而为飞行器侧向力、偏航力矩乃至控制横侧特性研究奠定基础。

4.2   层流翼型绕流

张彦军等^[34]采用数值模拟方法对NLF(1)-0416自然层流翼型在雷诺数变化下的层流-湍流转捩边界层特性开展了详细研究。

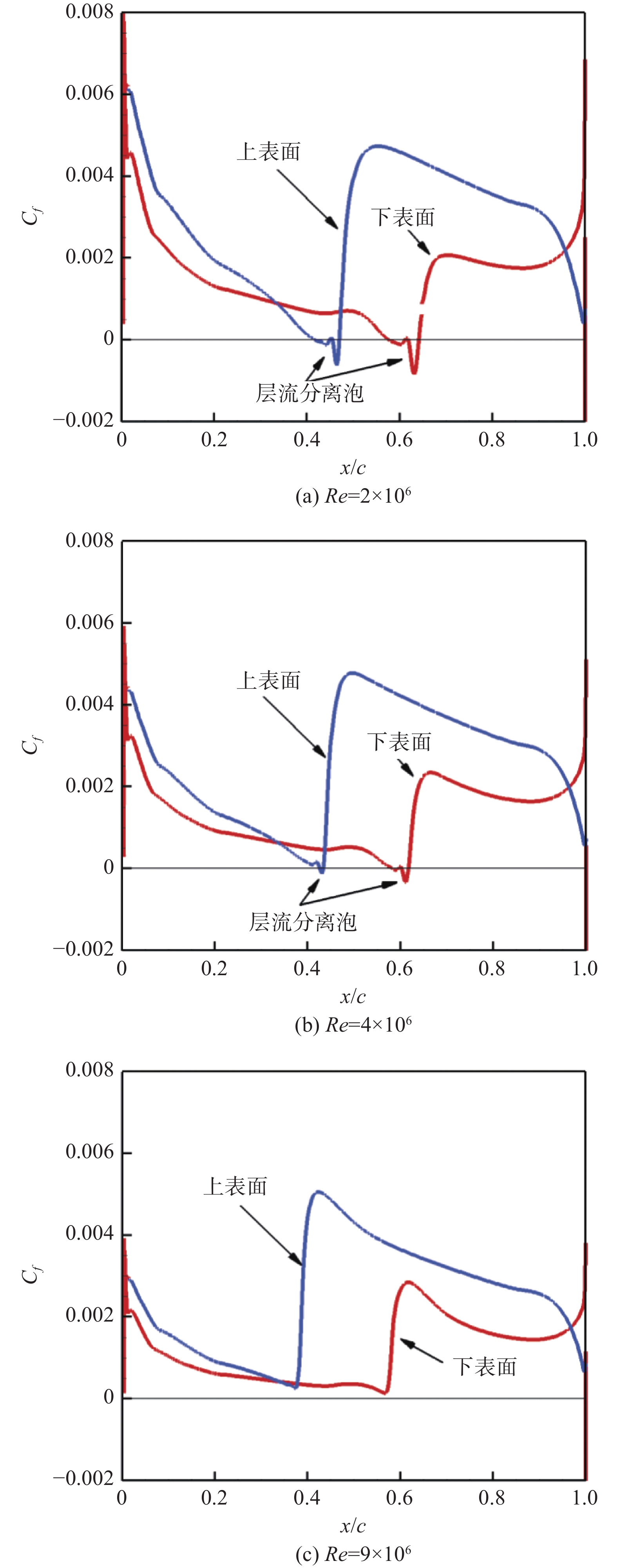
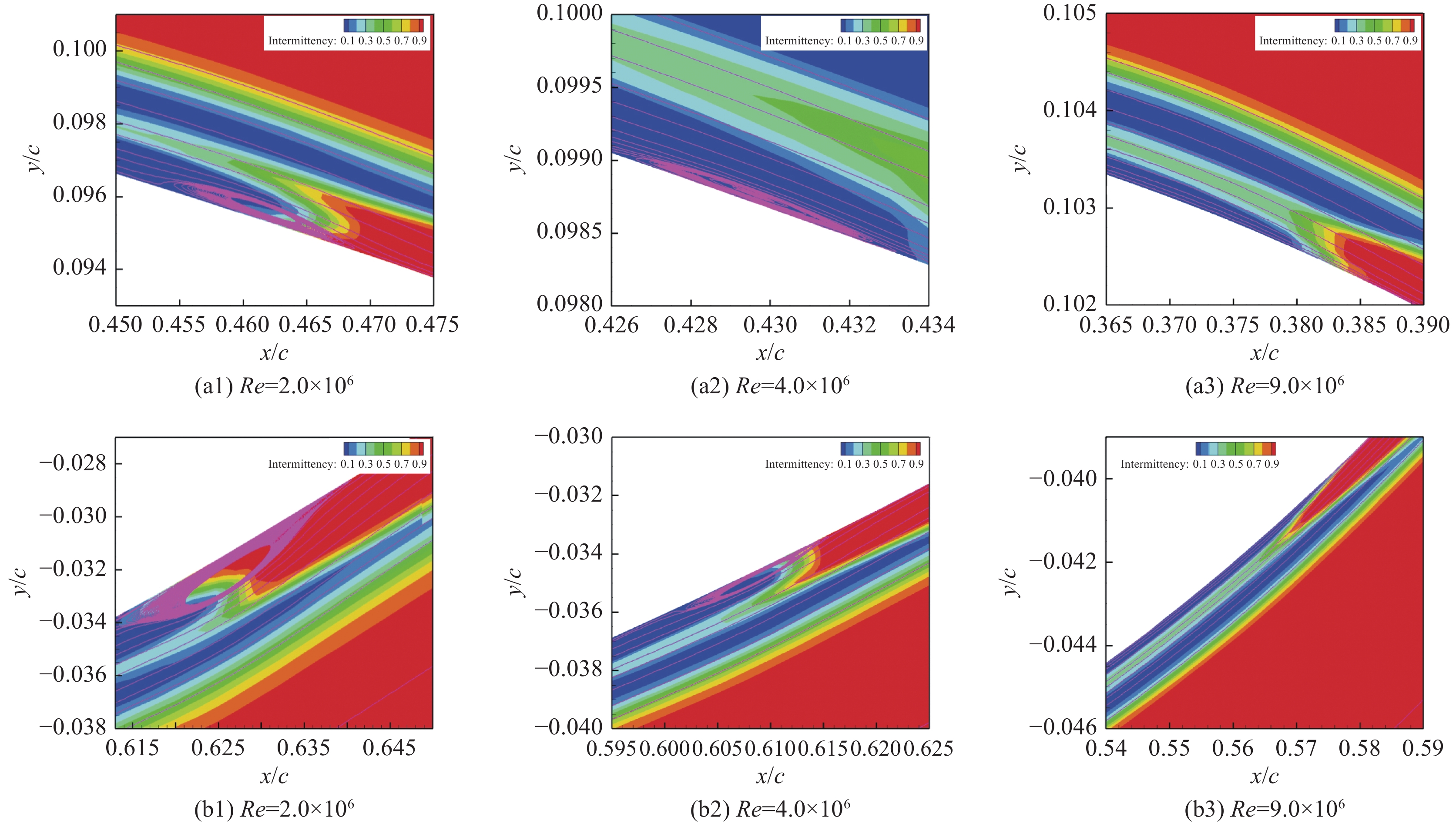
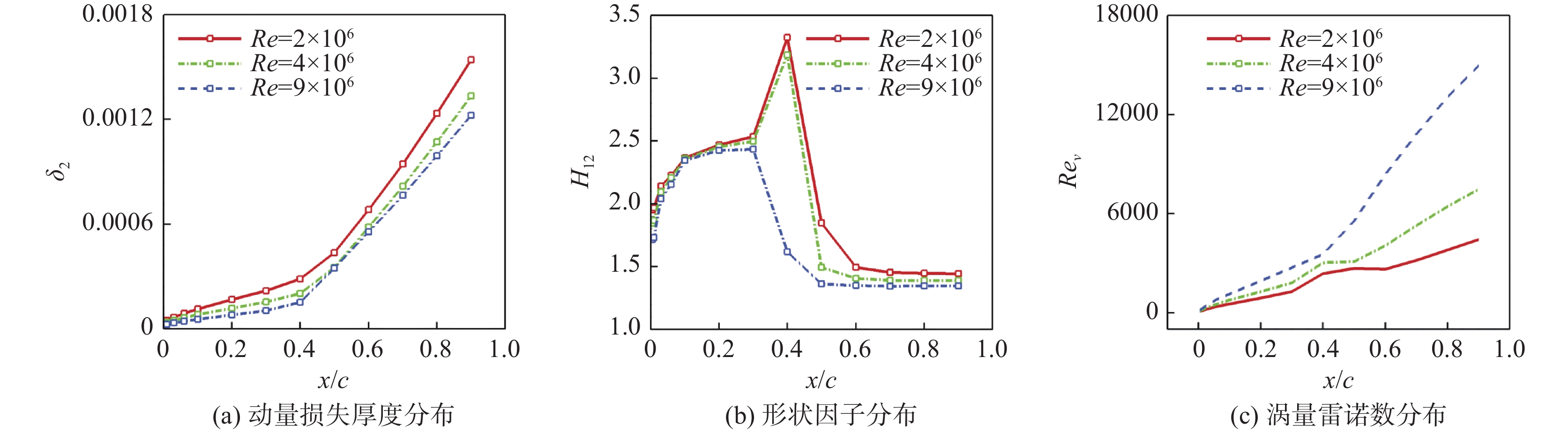
观察图21翼型层流分离泡形态，随着雷诺数增大，其上下表面的层流分离泡均逐渐减小，并在雷诺数为9 × 10⁶时，层流分离泡完全消失。观察图22翼型上表面边界层的动量损失厚度${\delta _2}$、形状因子${H_{12}} = {{{\delta _1}} \mathord{\left/ {\vphantom {{{\delta _1}} {{\delta _2}}}} \right. } {{\delta _2}}}$、涡量雷诺数${{Re} _\nu }$等参数分布，当雷诺数减小时，流动黏性作用增强，有利于边界层发展，使得动量损失厚度${\delta _2}$增大。在图22（b）中，边界层位移厚度${\delta _1}$在转捩后由于湍流边界层流速分布更趋均匀化而减小，同时动量损失厚度${\delta _2}$增大，因此边界层形状因子${H_{12}}$在转捩后减小，此外分离泡的出现引起40%弦长处出现峰值。在图22（c）中，边界层转捩触发位置随雷诺数升高而向前缘移动，并且在转捩后，涡量雷诺数${{Re} _\nu }$迅速增大，使边界层保持在湍流状态。观察图23相同迎角不同雷诺数下翼型流场的后缘分离情况，随着雷诺数增大，流动稳定性增强，抵抗逆压梯度干扰的能力提高，流动分离趋势较弱，这与前述观察到的边界层发展及其参数变化趋势一致。

图  21  0^o迎角翼型上、下表面转捩处流线及间歇因子云图^[34]

Figure  21.  Streamlines and intermittency factors around transition fronts at the upper and lower surfaces of a zero-angle-of-attack airfoil^[34]

下载: 全尺寸图片 幻灯片

图  22  0^o迎角上表面边界层不同参数分布^[34]

Figure  22.  Boundary-layer parameters along a zero-angle-of-attack airfoil^[34]

下载: 全尺寸图片 幻灯片

图  23  16^o迎角翼型流场流线图^[34]

Figure  23.  Streamlines around an airfoil with an angle-of-attack of 16° at different Reynolds numbers^[34]

下载: 全尺寸图片 幻灯片

5.   雷诺数效应问题的解决方法

前述内容较为全面地介绍了大型运输类飞机设计中所面临的高雷诺数问题，包括高速巡航阶段气动设计、低速起降阶段一些关键部件设计，以及与雷诺数效应相关的流动机理研究。为了解决雷诺数效应技术难题，通常有两种思路，一种是提高风洞试验能力和数据精度，直接解决雷诺数效应问题。另一种是研究修正技术，利用现有风洞和CFD数据进行修正，将风洞试验数据修正和外插到飞行雷诺数中。接下来首先分别介绍了先进风洞试验技术和雷诺数效应修正技术，最后介绍了人工智能技术给求解雷诺数问题带来的新的契机。

5.1   风洞试验技术

毫无疑问，解决雷诺数问题的最直接和最彻底的方案是直接进行雷诺数风洞试验，这一方案成本过高，对于大型飞机而言，全球各国目前还不具备该项能力。但是通过提高风洞试验雷诺数来逐步逼近飞行雷诺数是非常有效可行的方法，这是因为雷诺数增加到一定范围就会出现收敛区，继续增加雷诺数对飞机的流场和气动特性影响不再敏感。为此，各国都在不遗余力地发展高雷诺数大尺寸风洞，如前文所述的美国NASA的80 foot × 120 foot超大型风洞，可以大幅提升试验雷诺数，为飞机研发提供可靠的数据；为了提升风洞试验雷诺数范围，欧盟研发了ETW风洞^[49]，该风洞采用了低温增压技术使得试验范围大幅提升，全模试验雷诺数高达5000万，半模状态试验雷诺数可达8500万，风洞同时具备很高的流动品质和参数控制精度，已经成为高雷诺数试验的标杆。在2007 年大飞机专项工程正式立项研制时，我国气动力试验设备基础、试验模拟能力和试验数据修正技术均与美欧航空发达国家差距明显，低速风洞仅有4.5 m × 3.5 m连续增压风洞，亚跨声速仅有一座2.4 m × 2.4 m 常规暂冲型风洞。近年来随着我国经济快速增长，对大型飞机等航空航天装备的需求日益强烈，规划和建设了一批先进的风洞设备，如中国空气动力研究与发展中心的CTW风洞，航空工业气动院的FL-62风洞，使试验能力大幅提升，可以比肩欧美发达国家。上述先进的风洞设备大幅提升了我国高雷诺数试验能力，为雷诺数效应研究和大型飞机研发奠定了坚实的基础^[50]。

伴随着风洞技术的发展，近年来先进的测量技术也在高速进步，逐渐应用于机理研究和型号研发，如例子图像测速（particle image velocimetry, PIV）技术、压力敏感涂料（pressure sensitive paint, PSP）技术、各种先进的转捩测量以及边界层测量技术，同时数据测采集和处理也更加先进，为研究雷诺数效应对飞机转捩、分离及边界层影响提供了有力的支撑。此外，CFD技术也为风洞试验提供了技术支撑，一方面可以指导风洞试验，提升风洞数据的可靠性和试验效率；另一方面，两者可以相互校验，进一步增加彼此的可信度，消除数据的不确定性。

5.2   雷诺数效应修正技术

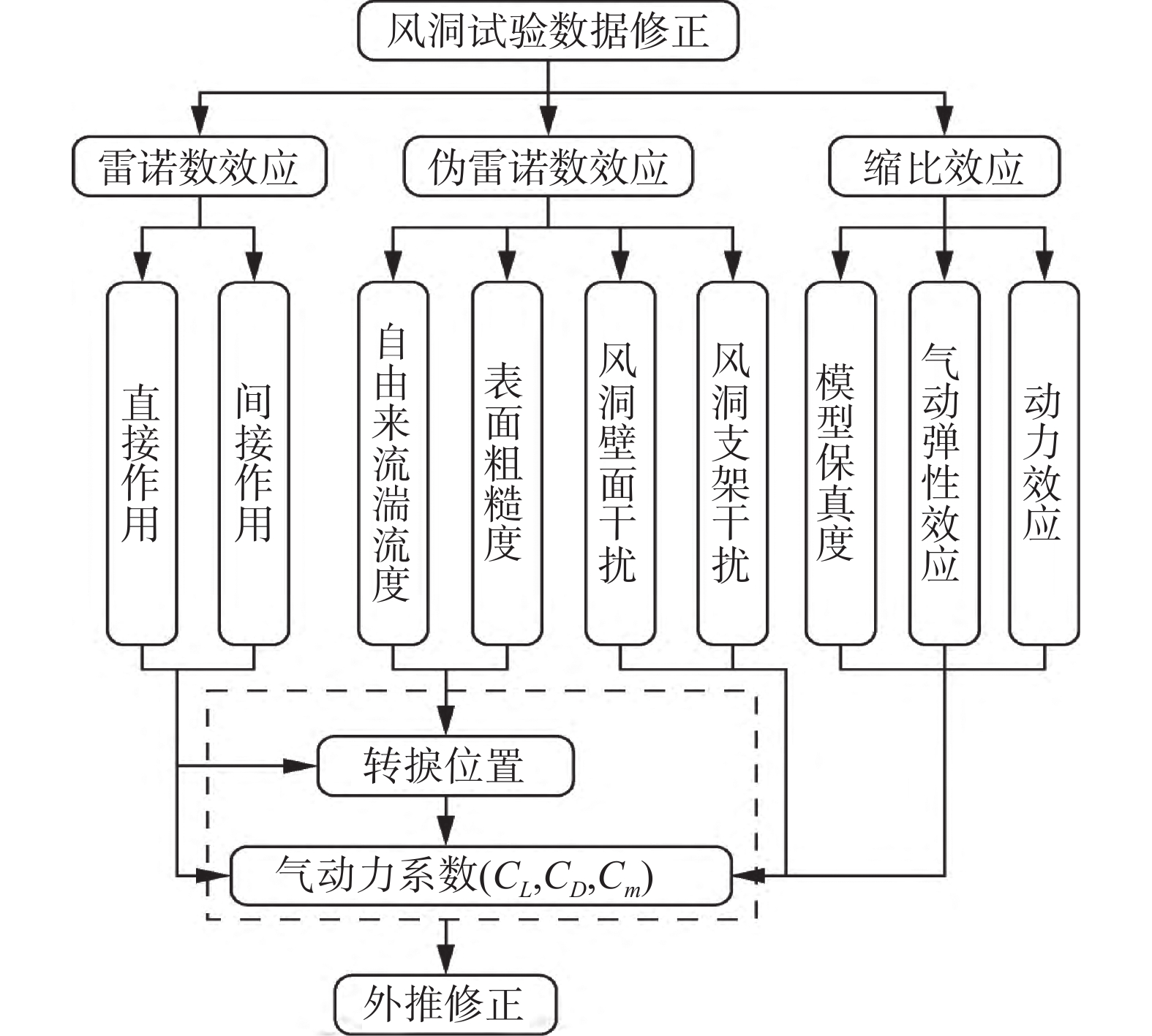
解决雷诺数效应问题最为有效的方法是建立风洞试验、CFD数值模拟和飞行试验三者之间的关联模型，支撑雷诺数效应分析及风洞试验数据修正^[51]。风洞试验数据修正中除了需要考虑雷诺数效应，还需要考虑伪雷诺数效应和缩比效应，如图24所示。

图  24  风洞试验数据修正示意图^[13]

Figure  24.  Schematic diagram of wind tunnel test data correction^[13]

下载: 全尺寸图片 幻灯片

伪雷诺数效应包括自由来流湍流度、表面粗糙度、风洞壁面干扰及支架干扰等因素所产生的影响^[52]；缩比效应是与模型保真度、气动弹性效应及动力效应等相关因素产生的影响^[53]。这两类影响的修正通常是由风洞试验人员给出或由相关经验公式表示^[13]。由于大型运输类飞机超临界翼型/机翼的流动特征对雷诺数差异最为敏感^[54]，因此风洞试验数据修正的重点主要集中在雷诺数效应。在对雷诺数效应的分析及修正中，主要针对的是常规风洞试验的气动力系数修正。在此基础上，研究人员会考虑雷诺数对流动转捩位置、激波强度和位置等的影响，其通过改变飞机表面压力分布，进而也会间接影响到全机的流场及气动特性。下面分别介绍了几种常用的雷诺数修正方法：

（1）基于经验公式的修正方法^[55]

Covert等^[56]基于不可压缩流动假设构建了一个基于平板的半经验公式，将表面摩擦阻力（也称摩阻）与雷诺数进行关联，通过最大可用雷诺数下的阻力数据进行公式标定，得到了两种常用形式，分别是 Prandtl-Schlichting形式（式（1））和 Karman-Shoenherr（式（2））。

其中常数A由流动转捩位置确定。

为了将表面摩阻经验公式推广至可压缩流动，Sommer等^[57]提出了$T'$方法，主要是借助Sutherland黏度公式将表面摩阻转化为适用于可压缩流动的形式。该部分工作对于一些高速飞行器的阻力预测非常必要，这是由于此时可压缩效应不可忽略且表面摩阻占比较大^[58]。

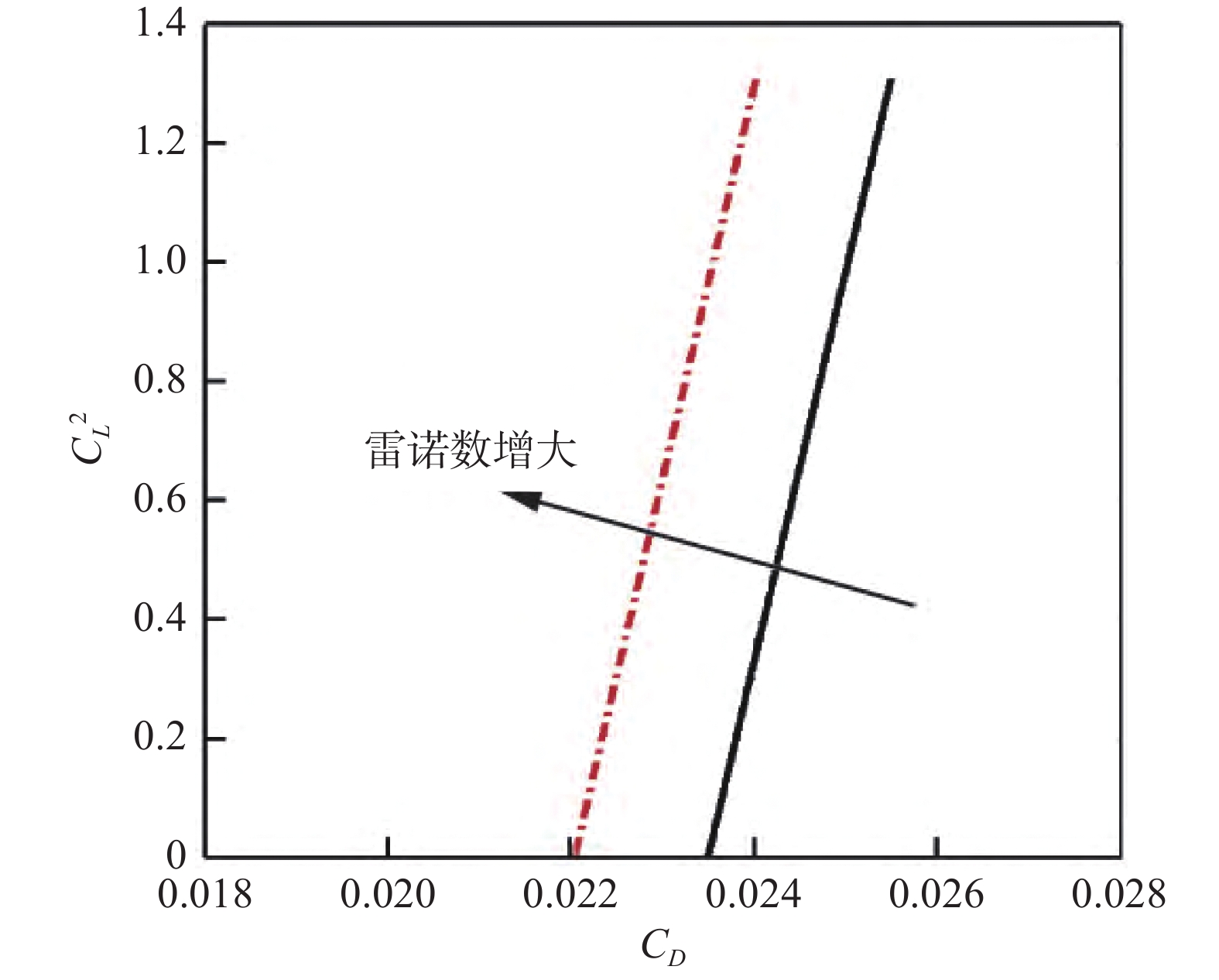
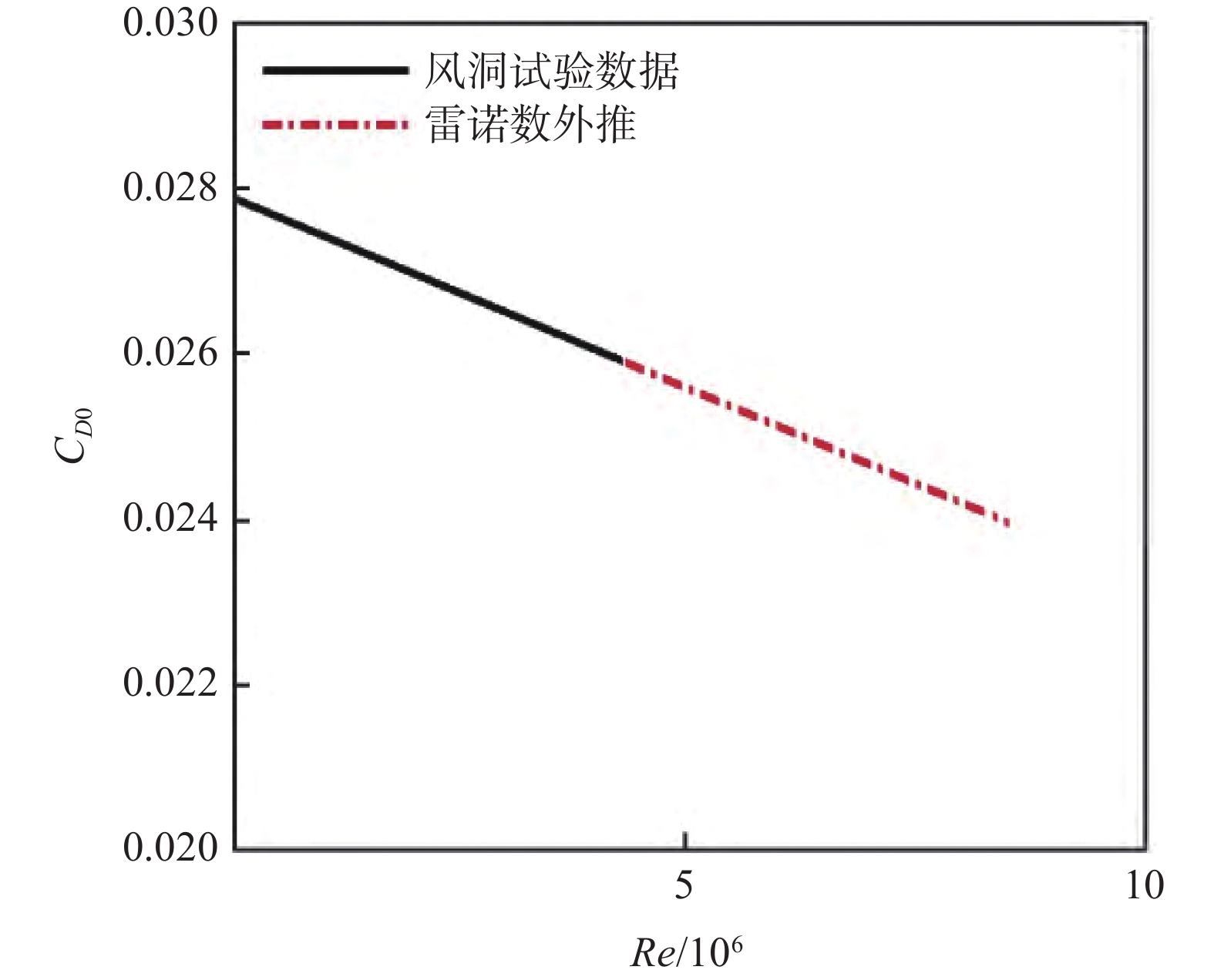
文献[13]中指出，对于一些翼型/机翼等简单附着流情况，其$C_L^2 \sim {C_D}$曲线与雷诺数呈现近乎线性变化趋势，如图25所示。由此提出一种基于雷诺数变化修正量的阻力平移修正方法。首先对已有风洞试验数据的零升阻力系数${C_{{D_0}}}$进行外推得到飞行雷诺数下零升阻力系数（如图26），接着借助该值标定图25中的曲线，确定$C_L^2 \sim {C_D}$曲线的偏移量，最后对阻力系数进行平移修正。

图  25  $C_L^2 \sim {C_D}$随雷诺数的变化趋势^[13]

Figure  25.  Reynolds number effects on the relationship between$C_L^2$and${C_D}$^[13]

下载: 全尺寸图片 幻灯片

图  26  ${C_{{D_0}}}$由风洞试验雷诺数向飞行雷诺数外推示意^[13]

Figure  26.  Extrapolation of${C_{{D_0}}}$from wind tunnel test Reynolds numbers to flight Reynolds numbers^[13]

下载: 全尺寸图片 幻灯片

在风洞试验数据严重不足的情况下，可以采用Barlow等^[59]提出的一种常用零升阻力系数${C_{{D_0}}}$外插方法，如式（3）所示：

其中指数k为经验常数，研究^[60]表明k值选取依赖于所研究的具体问题。

可以看到，上述基于经验公式的修正方法由于做了过多简化假设，适用范围小且严重依赖于研究人员经验。相较之下，借助CFD手段辅助修正则可以大大扩展原有经验方法的适用范围并改善精度。

（2）结合CFD手段的修正方法

CFD数值计算不存在雷诺数效应问题，并且可以针对全尺寸飞机几何外形及完整飞行工况开展性能评估，因此能够非常有效地用于风洞试验数据修正和飞行试验对比校验中^[61]。

首先将介绍基于CFD的对比修正方法或直接插值修正方法。在借助CFD数值模拟辅助风洞试验数据修正（图27）之前，需要对CFD数值模拟进行评估，保证其计算结果与风洞试验所得的流场拓扑结构、气动力/力矩等数据的一致性，即在前缘固定转捩或湍流边界层假设前提下，CFD计算可准确模拟大型运输类飞机气动力/力矩随雷诺数的变化规律，变化量值也与风洞试验较为接近^[29]。此时可将二者在低雷诺数下的数据差量外推至飞行雷诺数下，得到修正后数据^[62]。具体步骤如下：

图  27  结合CFD的雷诺数修正流程^[9]

Figure  27.  Reynolds number correction process integrated into CFD^[9]

下载: 全尺寸图片 幻灯片

1） 进行风洞试验雷诺数下的飞机气动特性数值模拟；

2） 进行飞行雷诺数下飞机气动特性数值模拟；

3） 将数值模拟得到的飞行雷诺数与风洞试验雷诺数下气动特性差量叠加到风洞试验数据，即可得到飞机飞行雷诺数下的气动特性数据。

该方法适用范围广，可以较好地适用于大型运输类飞机中的风洞试验数据修正。

统一形式的空气动力系数修正方法。Nicoli等^[63]在VEGA小型飞行器研究中提出了一种基于CFD且具有统一形式的空气动力系数修正方法，如式（4）所示：

式中，${C_X}$表示气动力/力矩系数，常数a和b可通过CFD数值模拟和风洞试验数据拟合获得。该方法只基于已有数据集进行数学拟合插值，不能反映物理现象，其修正精度完全依赖于已有数据的可靠程度。

此外，由于式（4）采用相同的对数函数形式，该方法只能对合力（如总阻力、总升力等）进行修正，无法对压差阻力和摩擦阻力分别进行缩比修正。且由于全机力矩系数随雷诺数变化趋势没有明显规律，该方法也不适用于力矩系数修正。

分步修正方法。为了使得修正数据更加真实可靠并且能够反映出相关流动机理，研究人员提出了一种分步修正方法^[13,64]。以大型运输类飞机升力系数为例，首先通过风洞试验和CFD计算获得全机各个升力面的升力系数分量，接着使用升力面翼型的${C_{L,\alpha }}$和${C_{{L_{\max }}}}$对全机升力开展尺度修正，保持翼型和全机的上述修正量之比与翼型升力和全机总升力之比相一致，并结合风洞测量中相似的失速特性对应地调整失速曲线形态，最后延长曲线使其达到估计的飞行雷诺数，并给出最终升力系数修正量。

该方法一定程度上能够反映出相关流动机理，但应用过程繁琐，且要求设计人员具有丰富的数据修正经验，当机翼扰流三维效应过强时，该方法存在一定局限性^[13]。

5.3   人工智能技术在雷诺数问题中的应用

目前CFD在复杂流动的数值模拟中仍存在预测精度普遍不高的问题^[65]，但其优势在于样本覆盖面广，获取成本较低。相较而言，风洞试验数据更为稀疏，尤其是在高雷诺数下，越逼近真实飞行条件，数据的获取成本便会急剧增加。人工智能技术的高速发展为解决多种气动评估手段之间数据不均衡问题提供了技术保障。借助人工智能技术将现有的数值模拟、风洞试验以及飞行测试等不同来源、不同模态、不同形式的数据进行融合，能够为解决雷诺数效应问题实现天地一致性提供新的思路和手段。现有人工智能技术中适用于解决雷诺数问题的方法主要为有多源数据融合与迁移学习^[5]。

其中数据融合技术能够对多种不同来源数据进行建模，充分利用不同手段（数值模拟、风洞试验、飞行试验）气动数据的优势，在有限的数据样本和时间成本下融合得到具有更高精度与一致性的预测结果。迁移学习技术可以利用数据、任务之间的相似性，将在旧领域学习过的模式和知识通过信息迁移应用于新领域，实现特征共享，扩展数据应用范围。上述方法已广泛应用于气动力建模^[66-67]、多组分复杂流体分析^[68]、气动外形优化^[69-70]等领域。

通过人工智能技术促进三大气动评估手段的深度融合，已成为开展新一代飞行器研究的必然需求^[71]。尤其是面对未来更复杂的应用场景和更极端的飞行工况，人工智能的应用将成为改进大型运输类飞机气动设计的强有力工具。

当前针对大飞机雷诺数问题的人工智能技术应用较为有限，且多停留在初步尝试阶段，相关研究包括：Subel等^[72]采用迁移学习技术研究了变雷诺数Burgers亚网格尺度建模，实现了由小雷诺数到高雷诺数的数据迁移。赵寅等^[73]采用GA-Elman神经网络技术研究了雷诺数对民用飞机发动机排气温度影响，建立了基于神经网络的排气温度裕度模型，提高了预测精度和适应性。Yang等^[74]基于RAE 2822翼型，采用多保真度神经网络开展了雷诺数效应修正研究，该方法能够结合CFD数据和风洞试验数据，给出不同雷诺数下的压力分布和气动力的修正。宁晨伽等^[5]将多源数据融合和迁移学习方法应用到民机雷诺数修正中，采用该方法进行了变雷诺数数据融合和雷诺数外插修正研究，并在CHN-T1宽体运输机模型宽域高雷诺数气动力特性的快速准确预测中进行了验证，为复杂雷诺数修正和建模提供了可靠的工具。

总的来说，对于采用人工智能的雷诺数修正研究方兴未艾，目前还处于探索和发展阶段，需要结合大型飞机的设计研发，采用大量的数据和模型进行方法验证和改进。

6.   结论与展望

雷诺数问题是大型飞机研制中的工程难题，影响了飞机的飞行安全性、气动性能、研发效率和成本，其本质是雷诺数对湍流发展和演化的科学难题。本文从风洞试验雷诺数效应、飞机设计雷诺数问题和雷诺数效应修正等方面总结了该问题的研究进展。

1） 高速巡航状态下雷诺数效应对超临界翼型压力分布、全机气动特性尤其是阻力特性及力矩特性有显著影响，因此在大型运输类飞机气动设计中需要特别重视。

2） 低速起降阶段雷诺数效应主要影响的是翼型/机翼最大升力系数及失速形态，增升装置、翼梢小翼和涡流发生器的部件设计等，这些都是实现大型飞机安全起降的关键一环。

3） 当前雷诺数效应流动机理的研究较少，且多集中在简单外形，如旋成体、二维翼型等，对于大型飞机气动设计的指导价值有限，研究人员应当继续深入开展此方面研究。

4） 雷诺数效应问题解决办法包括先进的风洞试验技术、基于半经验公式和CFD的雷诺数效应修正技术、以及借助数据融合与信息迁移等人工智能技术的多源变雷诺数一致性建模方法，考虑到实现成本以及应用前景，人工智能技术或许将成为解决该问题的最佳途径。

雷诺数效应问题长期困扰流体力学研究和飞机设计，过去的研究大多从气动力宏观层面开展研究，未来借助于人工智能的强大能力、高可信度数值模拟技术及高性能风洞试验技术，从流场细节和演化方面开展研究，实现重大理论突破，将是该领域重要的研究方向。同时，雷诺数的影响也需要从单一的气动学科向气动结构耦合方向发展，从静态的性能影响向飞机动态特性及振动、噪声、主动流动控制等方向发展，从传统的常规布局向非常规布局发展。总之，雷诺数效应的研究将是一项长期的艰巨的科学与工程难题，也将随之飞机设计的要求不断深入发展。