旋翼风洞试验洞壁干扰参数影响及敏感性分析

刘向楠; 邵天双; 刘少腾

doi:10.7638/kqdlxxb-2024.0157

旋翼风洞试验洞壁干扰参数影响及敏感性分析

刘向楠^{1, 2, ,},
邵天双^{1, 2},
刘少腾^{1, 2}

1.
中国航空工业空气动力研究院，哈尔滨　150001
2.
低速高雷诺数气动力航空科技重点实验室，哈尔滨　150001

详细信息

通讯作者:
刘向楠（1987—），男，内蒙古赤峰人，高级工程师，研究方向：飞行器风洞试验技术. E-mail：liuxiangnan200851@163.com

中图分类号: V211.52
计量
- 文章访问数: 32
- HTML全文浏览量: 1
- PDF下载量: 17
出版历程
- 收稿日期: 2024-09-09
- 修回日期: 2024-11-01
- 录用日期: 2024-11-13
- 网络出版日期: 2025-02-25
- 发布日期: 2025-02-25
- 刊出日期: 2025-03-24

Analysis of impact and sensitivity of wall interference parameters in wind tunnel test of rotors

LIU Xiangnan^{1, 2, ,},
SHAO Tianshuang^{1, 2},
LIU Shaoteng^{1, 2}

1.
AVIC Aerodynamics Research Institute, Harbin　150001, China
2.
Key Laboratory of Aviation Technology for Aerodynamics for Low Speed and High Reynolds Number, Harbin　150001, China

摘要

摘要:
在旋翼风洞试验中，模型旋翼产生的下洗流在风洞洞壁的约束下会产生强烈的洞壁干扰。引起洞壁干扰的参数众多，为了探究各试验参数对洞壁干扰的影响，首先建立基于Heyson方法的洞壁干扰分析方法，并在中国航空工业空气动力研究院FL-10风洞的开、闭口试验段开展了验证试验，验证了方法的有效性；然后基于该方法分析了各试验参数对洞壁干扰的影响；最后基于Sobol算法计算了洞壁干扰量对各试验参数的灵敏度，揭示了其敏感程度。结果表明：桨毂中心越靠近风洞中心，洞壁干扰相对越小；开、闭口试验段的旋翼洞壁干扰影响相反，且开口段的洞壁干扰影响大于闭口段；前进比、拉力系数、旋翼模型尺寸为洞壁干扰的主要影响参数，其中前进比起主要作用，其总灵敏度达0.894，拉力系数和旋翼模型尺寸的总灵敏度系数分别为0.144和0.155，为次要影响参数。研究结果为揭示旋翼洞壁干扰影响机理提供了参考。
- 旋翼 /
- 风洞试验 /
- 洞壁干扰 /
- 灵敏度 /
- FL-10风洞
Abstract:
During rotor wind tunnel tests, the downwash flow generated by the model rotor produces significant wall interference due to the constraints imposed by the wind tunnel walls, with multiple parameters contributing to this interference. To investigate the impact of test parameters on the tunnel wall interference, an analysis method based on the Heyson approach was first established. Verification tests were conducted in both open and closed test sections of the FL-10 wind tunnel at the AVIC Aerodynamics Research Institute, confirming the effectiveness of the method. Subsequently, this method was utilized to analyze the parameter effects on tunnel wall interference. Finally, the Sobol algorithm was employed to calculate the sensitivity of wall interference to various test parameters. The results indicate that wall interference is minimized when the hub center is aligned with the wind tunnel center. The effects of wall interference on the rotor performance are opposite in open and closed wind tunnels, with more pronounced interference observed in the open tunnel. Among the investigated parameters, the advance ratio emerges as the most significant factor, exhibiting a sensitivity coefficient of 0.894. The thrust coefficient and the rotor model scale represent secondary influencing parameters, with total sensitivity coefficients of 0.144 and 0.155, respectively. These findings provide valuable insights into the mechanism of rotor-wall interference effects.
- rotor /
- wind tunnel test /
- wall interference /
- sensitivity /
- FL-10 wind tunnel

HTML全文

0. 引　言

洞壁干扰是指风洞壁面对试验模型周围流场产生的影响，这种影响会导致测量数据与实际飞行条件下的数据存在偏差。直升机旋翼模型由于存在复杂的下洗流场，其洞壁干扰特性相较于固定翼更为复杂，为了提高旋翼模型风洞试验数据的可靠性，研究人员针对旋翼洞壁干扰开展了大量研究工作。

最早的旋翼模型风洞试验洞壁干扰修正方法借鉴了固定翼模型的葛劳渥洞壁干扰修正法^[1]。该方法将旋翼简化为一个具有椭圆形载荷分布的等效机翼模型，但由于其忽略了复杂的旋翼尾迹，修正结果并不理想。此后，Heyson^[2-4]发展了适用于垂直起降飞行器的洞壁干扰修正方法，该方法基于势流理论，考虑了旋翼尾迹，同时采用偶极子线对尾迹进行了简化，取得了良好的修正效果。杨永东等^[5] 研究了Heyson法并进行了初步验证。美国国家全尺寸空气动力学综合设施（NFAC）采用Heyson方法对两个全尺寸风洞旋翼洞壁干扰效应进行研究^[6-7]，分析了洞壁干扰对主轴倾角以及风洞阻塞特性的影响。Kolaei等^[8]对不同入流角的倾转旋翼气动特性开展了试验研究，并采用Heyson算法对数据进行了修正。针对Heyson方法只对桨盘平面迎角进行修正的问题，Brooks使用旋涡分布模拟旋翼，能给出干扰量的空间分布^[9]。Langer等^[10]采用Brooks方法计算了不同构型风洞中的旋翼洞壁干扰量，并与飞行实测值进行对比，验证了方法的有效性。此外，Shinoda等^[11]使用S-76旋翼模型进行了全尺寸直升机旋翼测试，通过风洞壁压信息分析了旋翼尾迹与风洞洞壁的干扰作用。

随着计算流体力学（CFD）的发展，CFD方法被广泛应用到旋翼洞壁干扰计算中。何瑞恒等^[12]采用动量源方法分析了洞壁对旋翼性能及机身测压数据的影响，并与Heyson方法进行了比较。Biava等^[13-17]和Boffadossi^[18]采用CFD方法系统研究了孤立旋翼、旋翼/机身组合模型在风洞开、闭口试验段的洞壁干扰特性及对主轴倾角的修正量。Koning^[19]和Garofano-Soldado等^[20]基于CFD方法建立倾转旋翼洞壁干扰分析方法。Peterson等^[21]采用CFD/CSD耦合方法计算了旋翼桨叶非定常载荷特性，并与飞行试验和全尺寸风洞试验结果进行了比较，分析了三者的关联性。此外，涡粒子及自由尾迹方法也被应用在了旋翼的近壁面干扰计算中^[22-23]。

参数灵敏度分析是识别模型关键参数的重要手段，主要分为局部灵敏度分析和全局灵敏度分析方法^[24]。局部灵敏度分析方法无法考虑各变量之间的交互作用；而全局灵敏度分析方法可以分析多参数对模型输出的影响，适用于复杂模型参数灵敏度研究与分析，主要有回归法、方差法和Sobol法等。参数灵敏度分析在航空领域得到广泛应用^[25-26]，但对于洞壁干扰参数敏感性方面的研究较少。Walker等^[27-28]针对美国国家航空航天局兰利中心跨声速风洞分析了洞壁干扰对马赫数、雷诺数的敏感程度，进一步验证了洞壁干扰修正算法的修正效果。Tai等^[29]采用全局灵敏度分析方法分析了亚声速风洞飞机模型洞壁干扰对模型参数和风洞参数的灵敏度指数，以识别重要的洞壁干扰影响参数。

综上所述，目前针对旋翼洞壁干扰的研究主要集中在洞壁干扰的修正方法本身，洞壁干扰修正建模方法从简单到复杂，逐渐满足旋翼复杂洞壁干扰精细化分析需求，但在各参数洞壁干扰影响机理分析以及洞壁干扰对参数的敏感度分析方面研究不足。本文建立基于Heyson方法的洞壁干扰分析方法，在大型低速风洞开、闭口试验段中开展旋翼前飞配平试验，并对开、闭口试验段数据进行修正，验证算法有效性；在此基础上，分析各参数对洞壁干扰的影响，基于Sobol^[30]算法分析洞壁干扰参数灵敏度，揭示旋翼洞壁干扰影响机理。

1. Heyson洞壁干扰修正方法

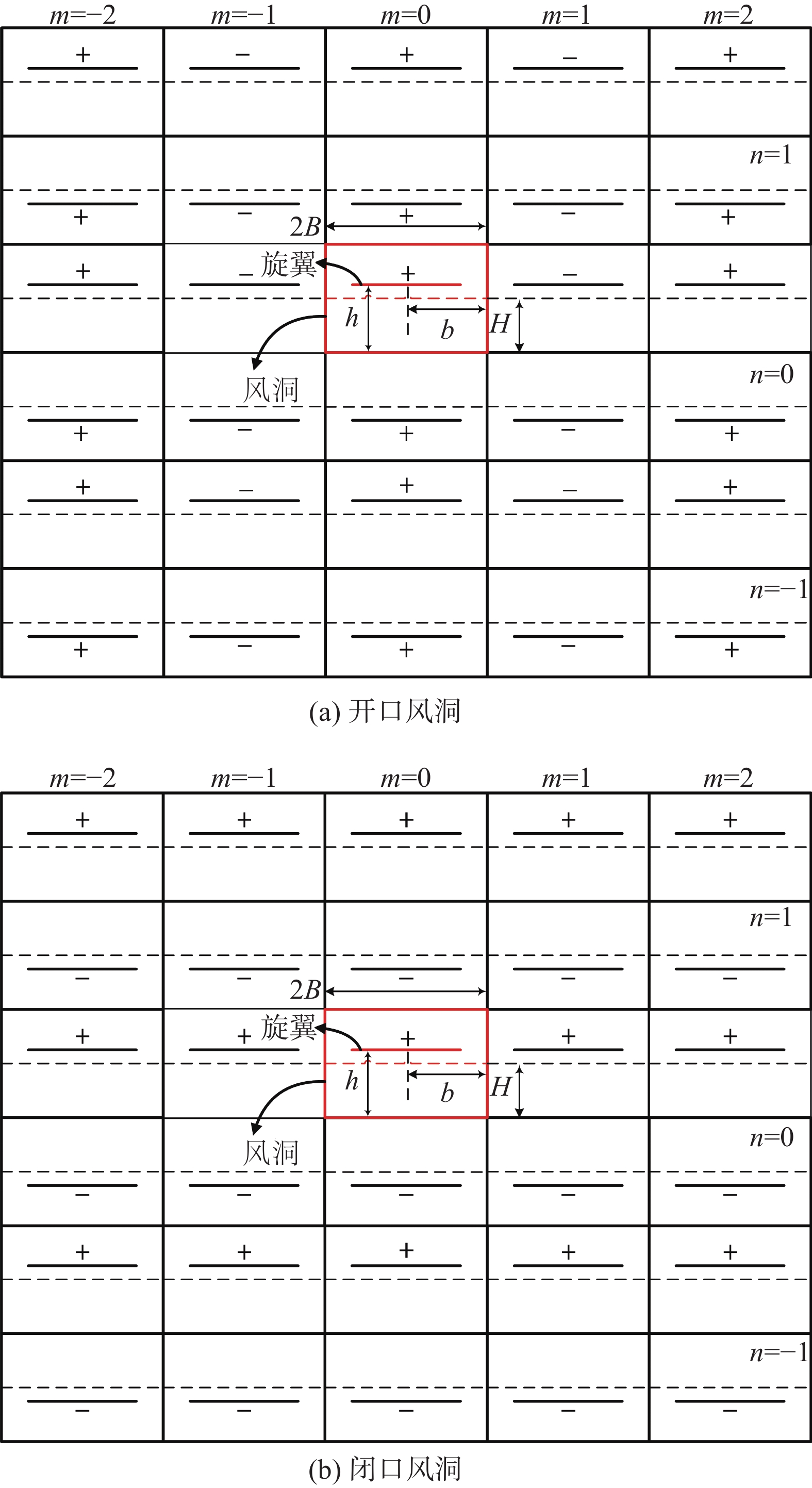
由于旋翼洞壁干扰修正主要针对旋翼性能，修正量主要为旋翼全局桨盘迎角，所以采用Heyson方法进行建模，分析洞壁干扰影响特性。Heyson洞壁干扰修正的基本思想是将旋翼尾流表示为半无限长的偶极子，通过建立不同的映像系统反应不同的风洞壁面边界对旋翼尾流的影响，如图1所示。闭口风洞映像和原像相反，满足法向速度为零的边界条件；开口风洞映像和原像相同，满足压力梯度连续的边界条件。在任意映像截面（m，n）处布置映像，则映像距离原像垂向距离为4nH，横向距离为 $2m\gamma H -\gamma H(1 - \eta ) [1 - {( - 1)^m}]$ ，其中，H为风洞高的一半， $\gamma = B/H$ ， $\eta = b/B$ ，B为风洞宽度的一半， b为桨毂中心距离右侧壁面距离。此外，图1中，h为桨毂中心距风洞下壁面高度。

图 1 不同风洞形式映像系统

Figure 1. Image systems of different wind tunnel configurations

下载: 全尺寸图片幻灯片

将整个系统映像后叠加，则洞壁干扰因子如式（1）所示：

$\begin{split} \delta=&-\zeta^2 \frac{2 \gamma}{{\text{π}}} \Bigg\{\sum _ { \substack { n = - \infty } } ^ { \infty } \sum _ { \substack { n = - \infty \\ m = n \neq 0 } } ^ { \infty } ( - 1 ) ^ { p } \left\{K \left[\zeta \frac{x}{H}, \zeta\left(\frac{y}{H}-2 m \gamma+\gamma(1-\eta)\left(1-(-1)^m\right), \zeta\left(\frac{z}{H}-4 n\right)\right]\right.\right.- \\ & K\left[\left(\zeta \frac{x}{H}-\tan \chi\right), \zeta\left(\frac{y}{H}-2 m \gamma+\gamma(1-\eta)\left(1-(-1)^m\right)\right), \zeta\left(\frac{z}{H}-4 n\right)+1\right] -\\ & (-1)^q K\left[\zeta \frac{x}{H}, \zeta\left(\frac{y}{H}-2 m \gamma+\gamma(1-\eta)\left(1-(-1)^m\right)\right),-\zeta\left(\frac{z}{H}-4 n\right)-2\right]+ \\ & (-1)^q K\left[\left(\zeta \frac{x}{H}-\tan \chi\right), \zeta\left(\frac{y}{H}-2 m \gamma+\gamma(1-\eta)\left(1-(-1)^m\right)\right),-\zeta\left(\frac{z}{H}-4 n\right)-1\right]+ \\ & \left.\left.2 s K\right|_{\chi=90^{\circ}}\left[\left(\zeta \frac{x}{H}-\tan \chi\right), \zeta\left(\frac{y}{H}-2 m \gamma+\gamma(1-\eta)\left(1-(-1)^m\right)\right), \zeta\left(\frac{z}{H}-4 n\right)+1\right]\right\}+ \\ & \left\{ - K\left[\left(\zeta \frac{x}{H} - \tan \chi \right),\zeta \frac{y}{H},\zeta \frac{z}{H} + 1\right] - {\left( - 1\right)^q}K\left[\zeta \frac{x}{H},\zeta \frac{y}{H}, - \zeta \frac{z}{H} - 2\right]\right.+\\ & \left.(-1)^q K\left[\left(\zeta \frac{x}{H}-\tan \chi\right), \zeta \frac{y}{H},-\zeta \frac{z}{H}-1\right]+\left.2 s K\right|_{\chi=90^{\circ}}\left[\left(\zeta \frac{x}{H}-\tan \chi\right), \zeta \frac{y}{H}, \zeta \frac{z}{H}+1\right]\right\}\Bigg\} \end{split}$

(1)

式中： $\zeta = H/h$ ， $\chi$ 为旋翼尾流偏斜角；K为空间任意点M(x, y, z)诱导速度的函数；p、q、s为远场诱导速度与模型处诱导速度的整数比，取值如所示，根据风洞形式不同而不同。中 ${\delta _{w,{\mathrm{L}}}}$ 、 ${\delta _{w,{\rm{D}}}}$ 为垂向诱导速度产生的洞壁干扰因子， ${\delta _{v,{\rm{L}}}}$ 、 ${\delta _{v,{\rm{D}}}}$ 为流向诱导速度产生的洞壁干扰因子。

表 1 不同风洞形式p、q、s取值

Table 1. Values of p, q, s with different wind tunnelconfigurations

风洞形式	洞壁干扰因子	p	q	s
闭口	${\delta _{w,{\rm{L}}}}$	0	0	0
	${\delta _{v,{\rm{L}}}}$	0	1	0
	${\delta _{w,{\rm{D}}}}$	0	0	1
	${\delta _{v,{\rm{D}}}}$	0	1	1

开口	${\delta _{w,{\rm{L}}}}$	m	1	1
	${\delta _{v,{\rm{L}}}}$	m	0	1
	${\delta _{w,{\rm{D}}}}$	m	1	0
	${\delta _{v,{\rm{D}}}}$	m	0	0

下载: 导出CSV

| 显示表格

由洞壁干扰因子得到桨盘中心处垂向和流向的干扰速度值分别如式（2）和式（3）所示：

${{\Delta }}w = {\delta _{w,{\rm{L}}}}\frac{{{A_{\mathrm{m}}}}}{{{A_{\mathrm{T}}}}}{w_0} + {\delta _{w,{\rm{D}}}}\frac{{{A_{\mathrm{m}}}}}{{{A_{\mathrm{T}}}}}{v_0}$

(2)

${{\Delta }}v = {\delta _{v,{\rm{L}}}}\frac{{{A_{\mathrm{m}}}}}{{{A_{\mathrm{T}}}}}{w_0} + {\delta _{v,{\rm{D}}}}\frac{{{A_{{\mathrm{m}}}}}}{{{A_{\mathrm{T}}}}}{v_0}$

(3)

其中，A_m为旋翼模型桨盘面积，A_T为风洞横截面积，w₀、v₀分别为旋翼中心垂向和流向诱导速度。

洞壁干扰引起的修正角如式（4）所示：

$\Delta \alpha = \arctan \frac{{\Delta w}}{{v + \Delta v}}$

(4)

其中v为风洞来流风速。

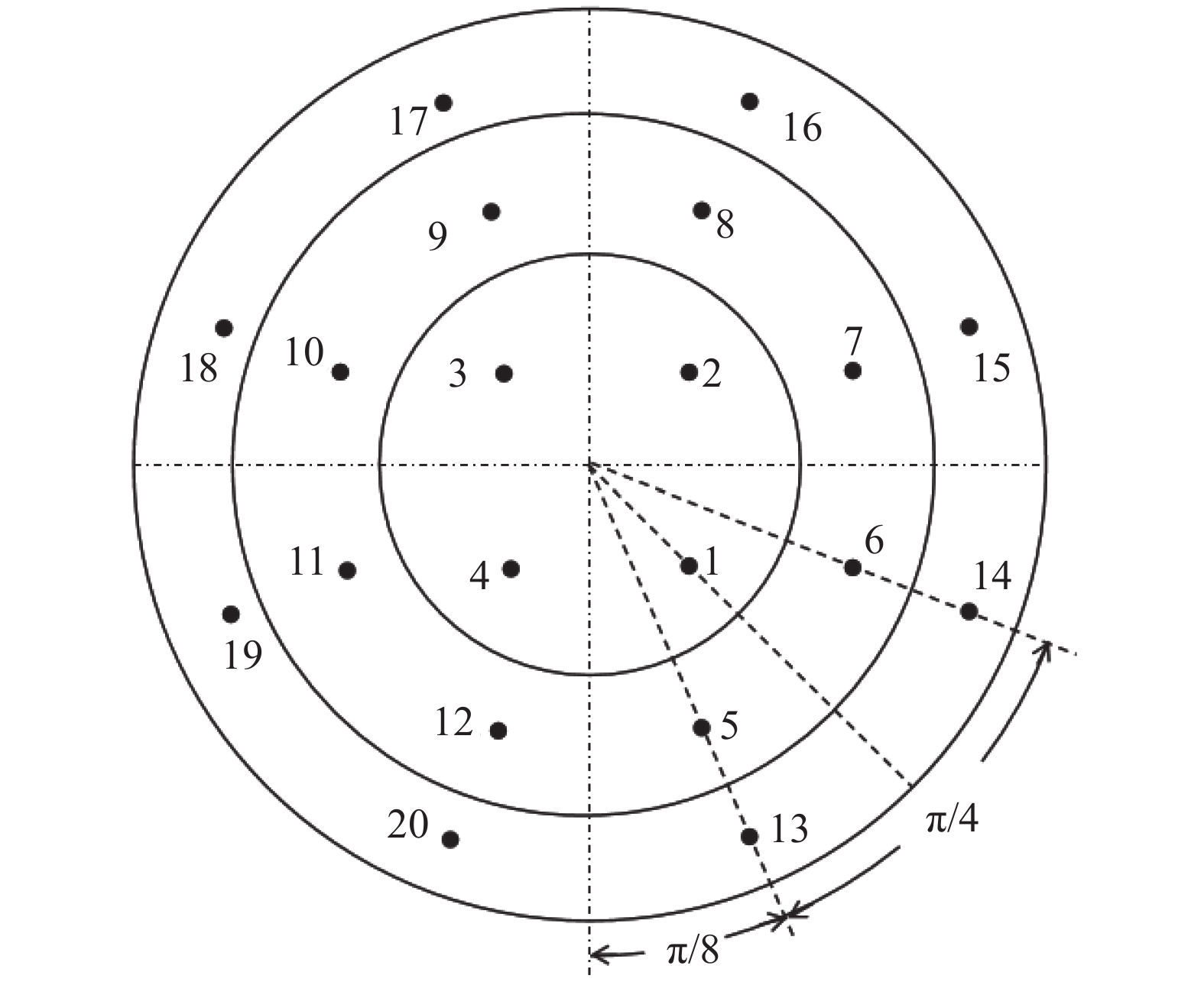
对于旋翼模型，将桨盘离散为小的区域，对于每个区域控制点，计算其他所有尾流对其的干扰，然后将所有控制点干扰叠加后平均，即可得到旋翼桨盘处的平均干扰量。如图2所示，采用桨盘载荷均匀分布开展旋翼洞壁干扰特性分析，将桨盘离散为20个面积相等的区域，控制点位于各区域中心。

图 2 旋翼桨盘控制点分布

Figure 2. Distribution of control points on the rotor disk

下载: 全尺寸图片幻灯片

2. 旋翼洞壁干扰计算方法验证

本文在航空工业空气动力研究院FL-10风洞开、闭口试验段开展了配平前飞试验，验证洞壁干扰修正方法的有效性。

2.1 风洞和模型

FL-10风洞尺寸为20 m（长）×8 m（宽）×6 m（高），具备开、闭口试验段，具备直径为4 m量级的旋翼模型气动及气动噪声试验能力。旋翼模型采用BO-105 型直升机的40%缩比模型，旋翼直径为4 m。安装在开闭口试验段的模型如图3所示。

图 3 在FL-10风洞开、闭口试验段中的旋翼模型

Figure 3. Rotor model set-up in the open and closed test sections of the FL-10 wind tunnel

下载: 全尺寸图片幻灯片

2.2 试验内容及方法

试验时，针对不同的前进比μ，固定主轴倾角α_s，配平垂向力系数C_w=0.005，同时保持桨毂力矩接近于0，试验悬停桨尖马赫数Ma_T=0.641，具体的试验状态如表2所示。

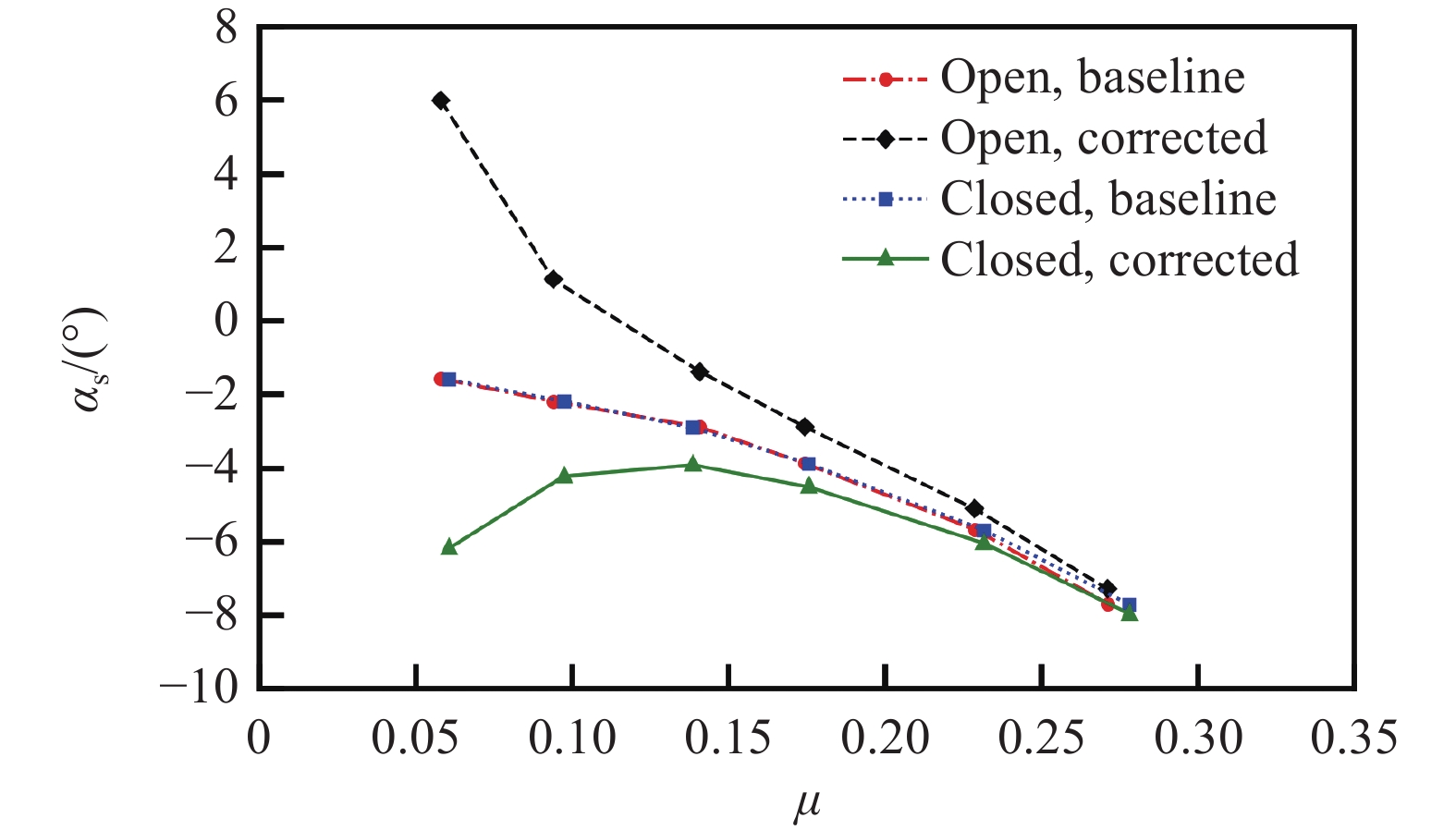
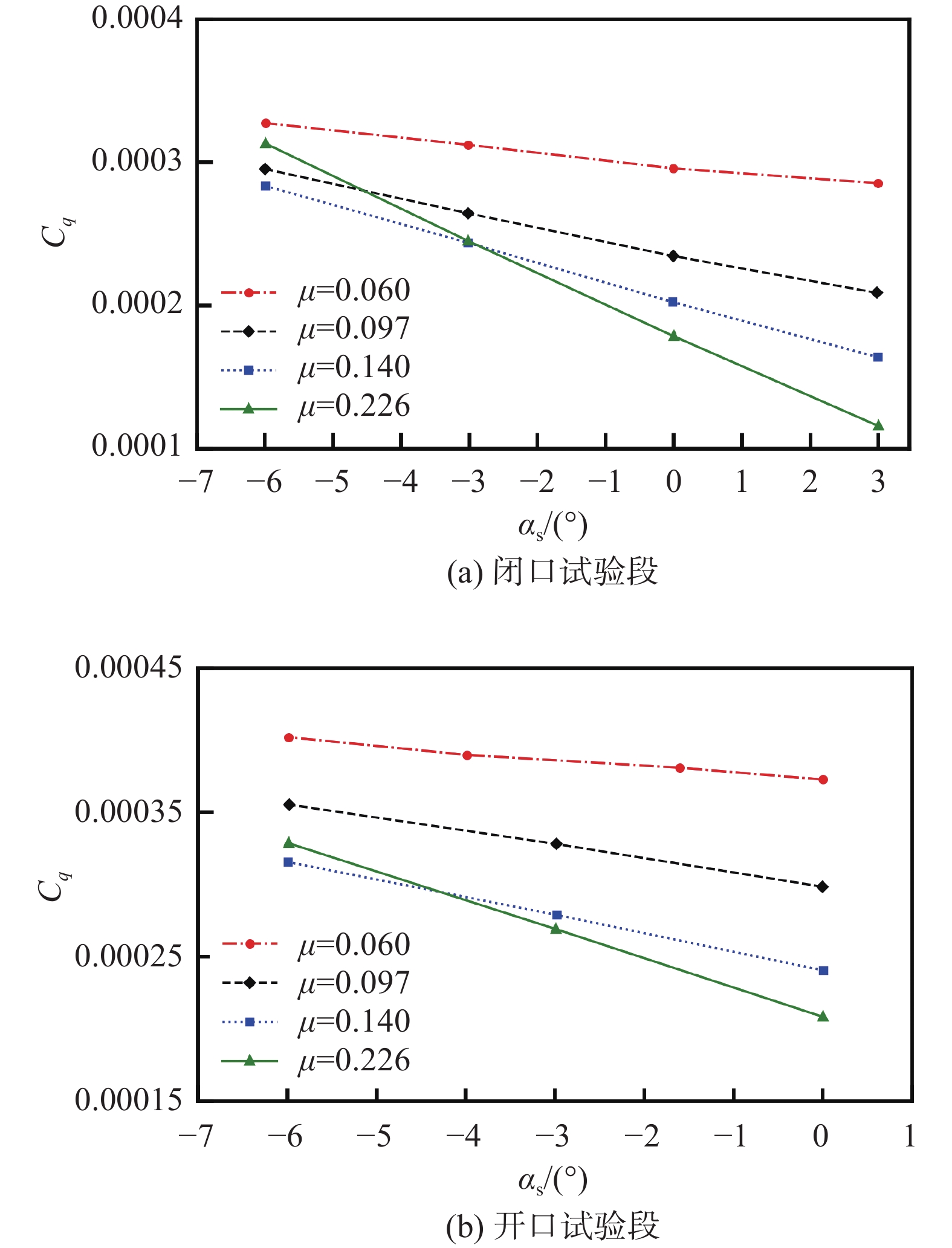
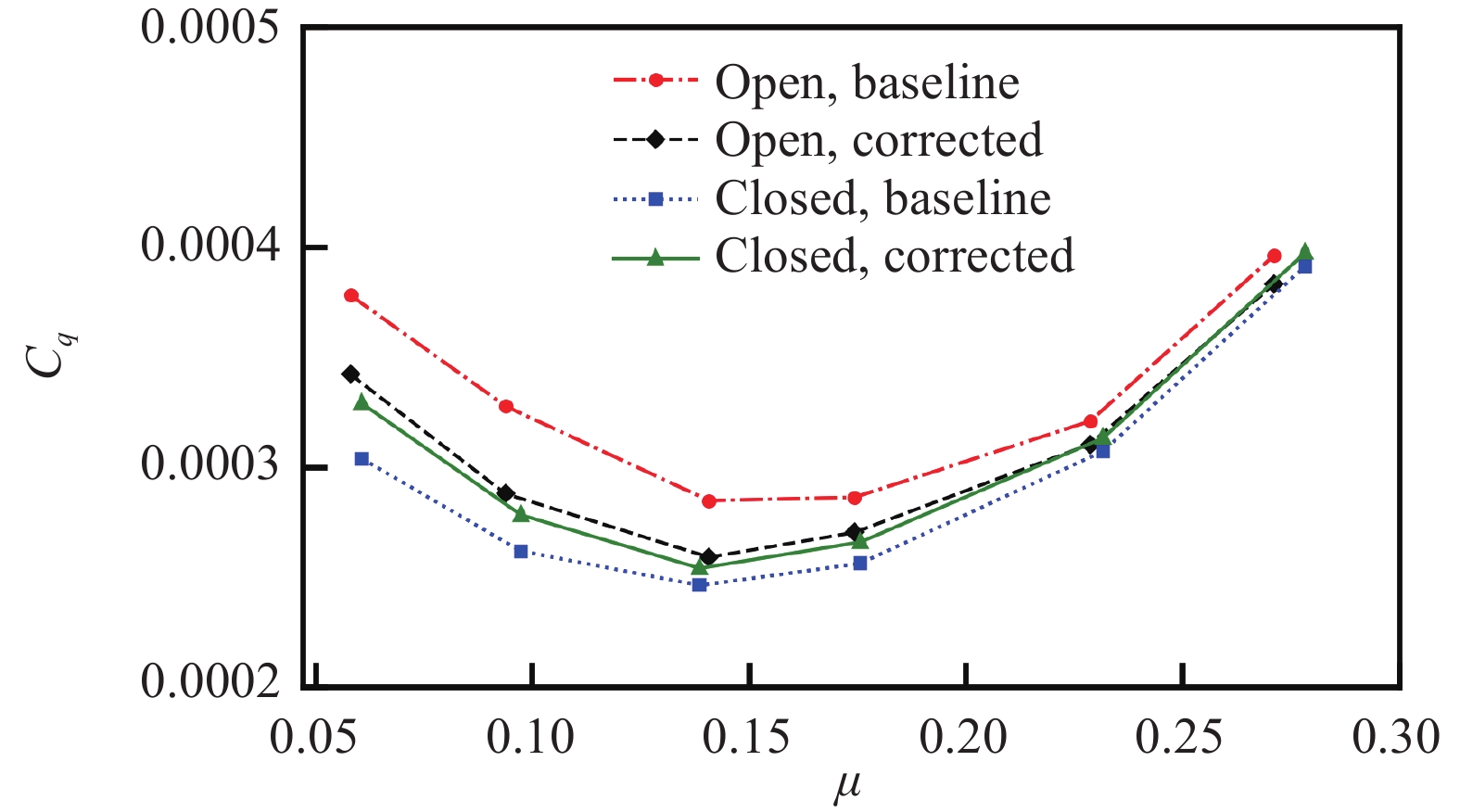
表 2 风洞试验状态

Table 2. Test conditions in the wind tunnel

μ	$\alpha_{\mathrm{s}}$ /(°)	C_w	${{Ma}}_{\mathrm{T}}$
0.059	–1.6	0.005	0.641
0.096	–2.2	0.005	0.641
0.136	–2.9	0.005	0.641
0.173	–3.9	0.005	0.641
0.227	–5.7	0.005	0.641
0.273	–7.7	0.005	0.641

下载: 导出CSV

| 显示表格

试验分别在风洞开、闭口试验段中进行，首先采用洞壁干扰修正算法计算出相应的修正角 $\Delta \alpha$ ，然后针对不同前进比改变旋翼主轴倾角，进而获得功率系数随主轴倾角的变化关系，通过修正后的角度得到对应的功率系数，最后对比开、闭口试验修正后的数据来验证算法的有效性。图4为开、闭口试验修正前后的主轴倾角对比，可以看出：小前进比时主轴倾角修正量较大，随着前进比增大，修正量逐渐减小，开、闭口试验修正量呈现相反的趋势。图5为开、闭口试验部分前进比功率系数随主轴倾角变化曲线，可以看出：旋翼功率系数随主轴倾角呈线性变化，根据修正角及功率系数与主轴倾角的变化关系可得到功率系数修正量。图6为开、闭口试验不同前进比下功率系数修正前后对比，可以看出：修正后，相同前进比下开、闭口试验功率系数趋近一致，说明了洞壁干扰修正方法的有效性。

图 4 开、闭口试验修正前后的主轴倾角对比

Figure 4. Comparison of the rotor main shaft tilt angles in the open and closed test sections before and after correction

下载: 全尺寸图片幻灯片

图 5 不同前进比下功率系数随主轴倾角的变化

Figure 5. The variations of the power coefficient with the shaft tilt angle under different advance ratios

下载: 全尺寸图片幻灯片

图 6 开、闭口试验修正前后的功率系数与前进比关系对比

Figure 6. Comparison of the relationship between the power coefficient and the advance ratio before and after correction in the open and closed test sections

下载: 全尺寸图片幻灯片

3. 旋翼洞壁干扰参数影响分析

本节基于Heyson洞壁干扰修正方法，分析典型参数对洞壁干扰的影响。

3.1 拉力系数的影响

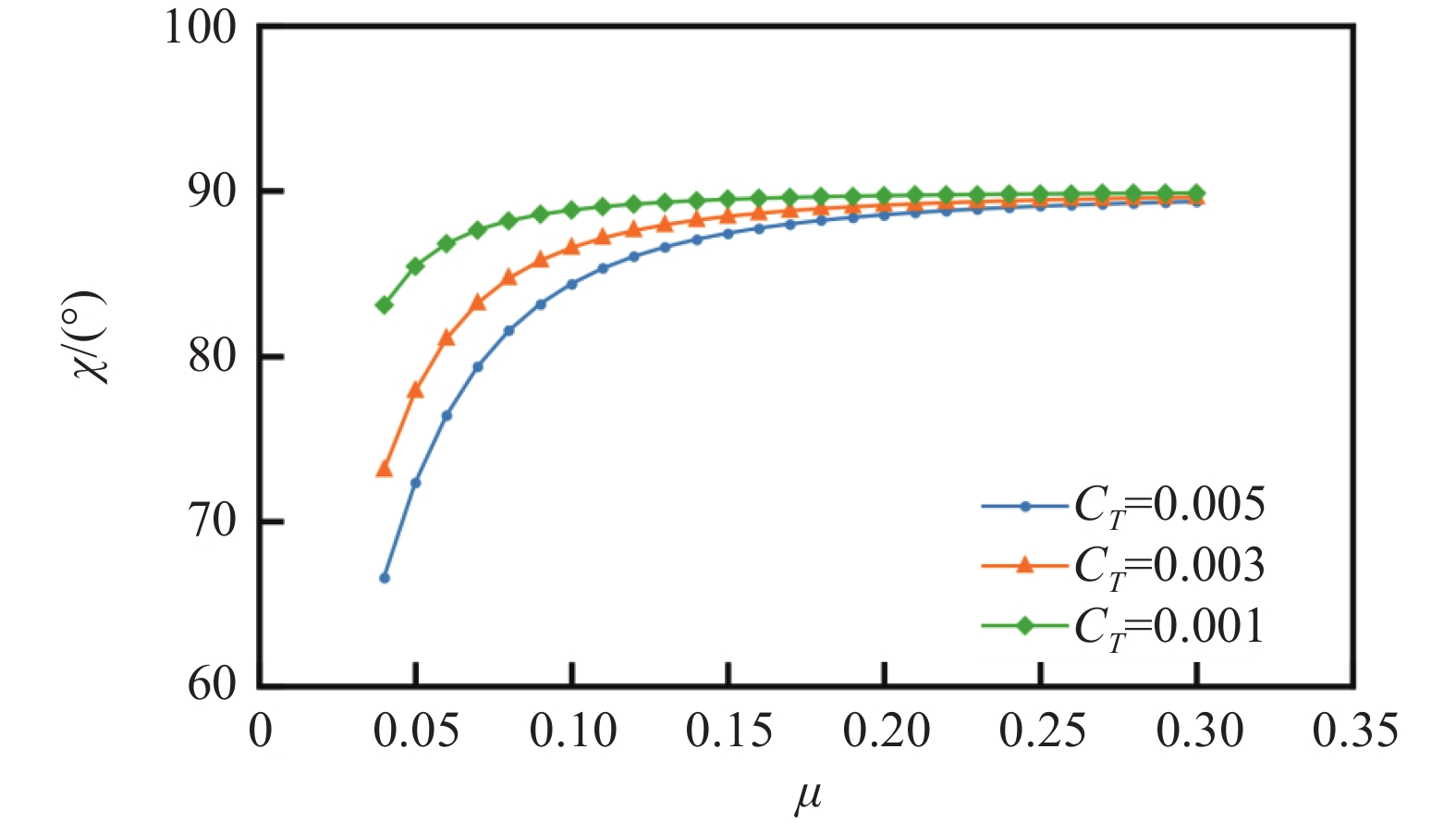
图7为闭口试验段不同拉力系数C_T下尾流偏斜角χ随前进比变化曲线，可以看出：相同前进比下，拉力系数越大尾流偏斜角越小，随着前进比增加，旋翼尾流偏斜角逐渐增大。这是因为随着拉力系数增大，旋翼垂向诱导速度逐渐增大，导致相同前进比下尾流偏斜角逐渐减小，而随着前进比增大，旋翼尾流流向分量逐渐增大，导致尾流偏斜角也逐渐增大，并逐渐趋近于90°。

图 7 不同拉力系数下尾流偏斜角随前进比变化

Figure 7. The variations of the wake deflection angle with the advance ratio under different thrust coefficients

下载: 全尺寸图片幻灯片

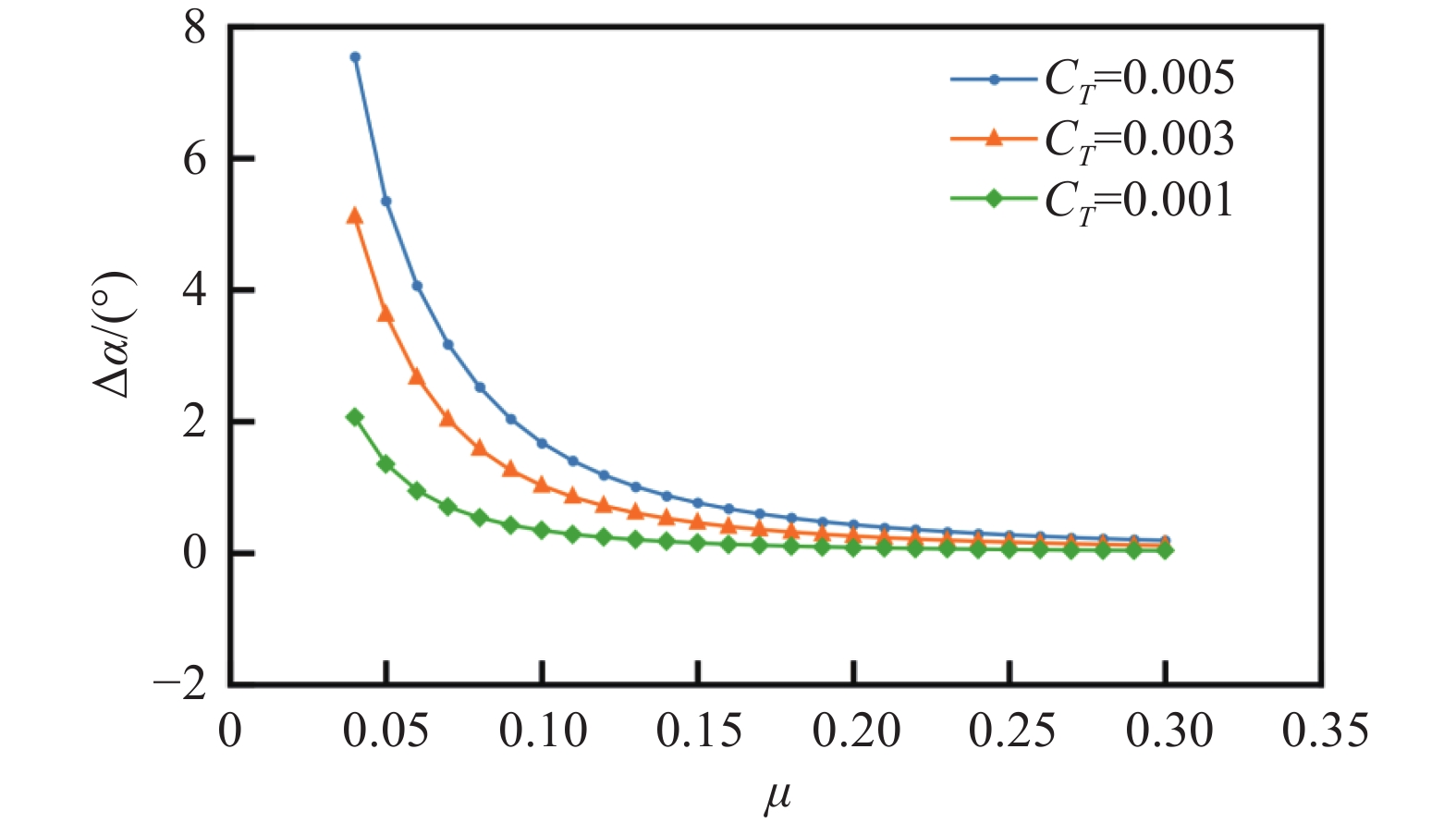
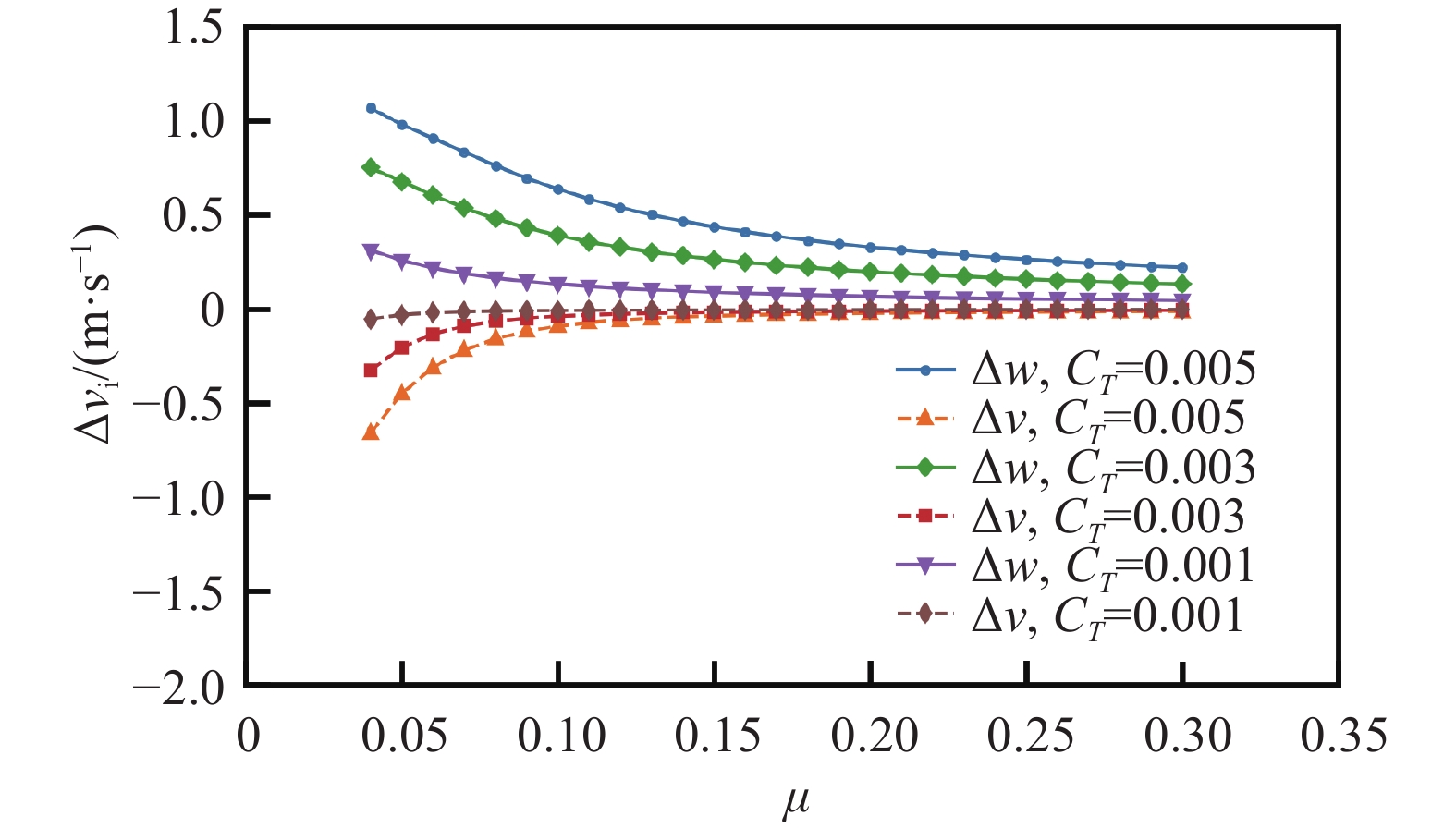
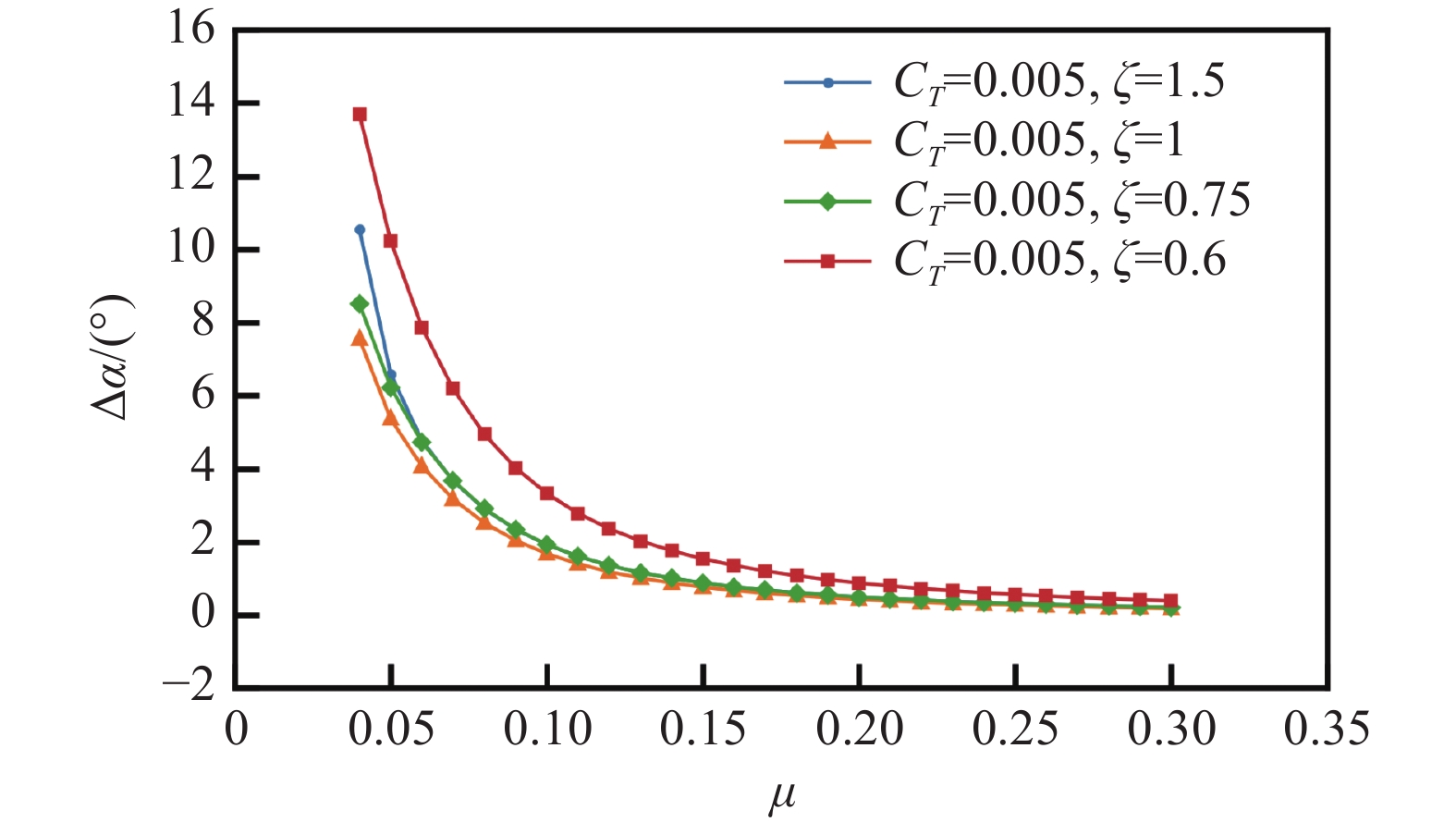
图8为不同拉力系数下修正角随前进比变化曲线。图9为闭口试验段不同拉力系数下桨盘中心处垂向和流向干扰速度随前进比变化曲线，其中，实线为垂向干扰速度Δw，虚线为流向干扰速度Δv。由图8可以看出：修正角随着前进比增大而减小，而前进比相同时拉力系数越大修正角越大。其原因可以由图9分析得到：随着前进比的减小，旋翼尾流与风洞下壁面的相互作用加剧，导致风洞壁面对旋翼产生的干扰速度效应愈发明显，垂向干扰速度相较于流向干扰速度变化更大，所以前进比越小，修正角越大；而拉力系数越大，干扰速度也越大，导致修正角也越大。同时，此时垂向干扰速度为正值，这会减小旋翼垂向诱导速度，意味着此时洞壁干扰对旋翼尾流的干扰作用表现为诱导气流上洗。

图 8 不同拉力系数下修正角随前进比变化

Figure 8. The variations of the corrected angle with the advance ratio under different thrust coefficients

下载: 全尺寸图片幻灯片

图 9 不同拉力系数下干扰速度随前进比变化

Figure 9. The variations of the interference velocity with the advance ratio under different thrust coefficients

下载: 全尺寸图片幻灯片

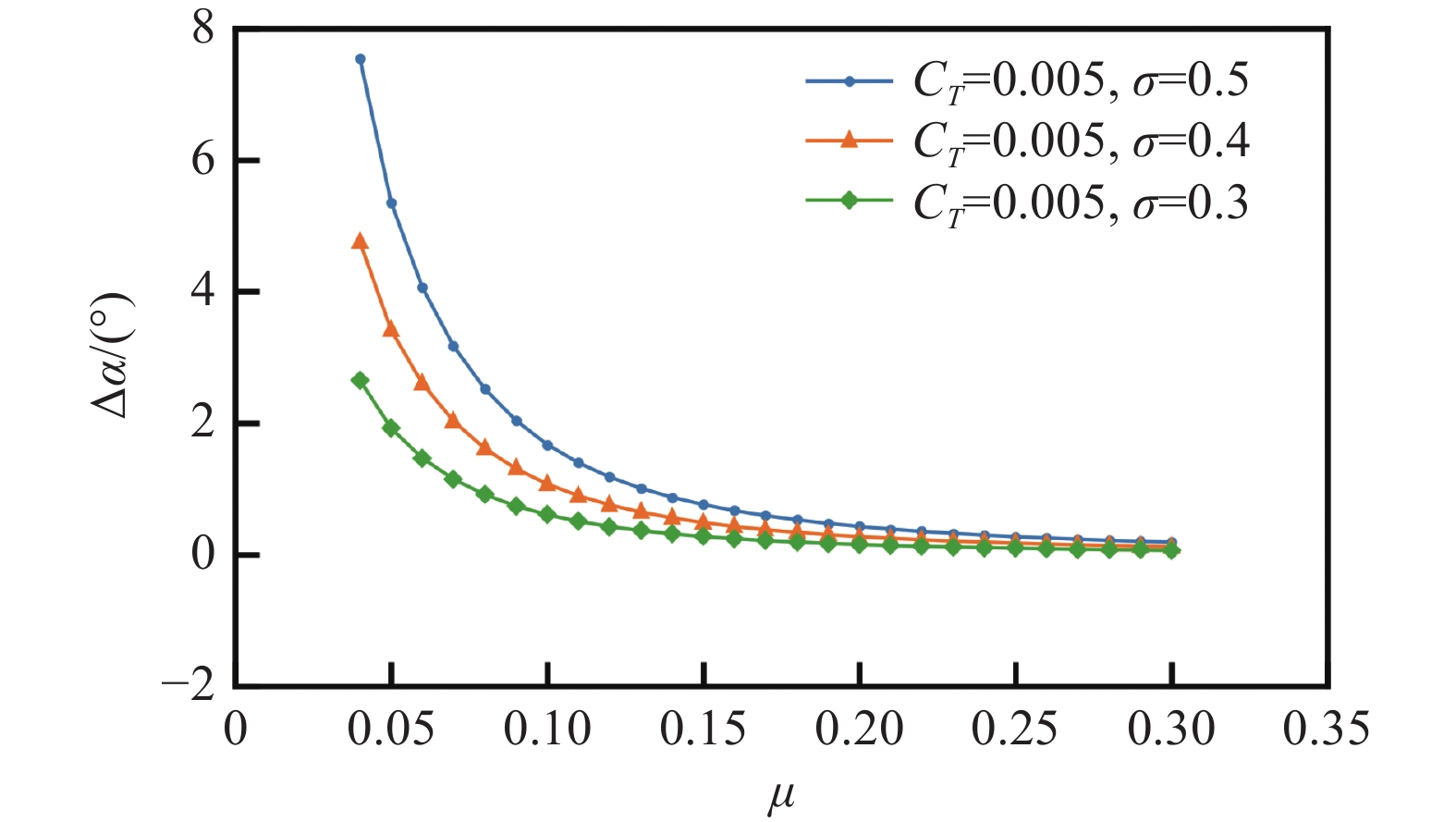
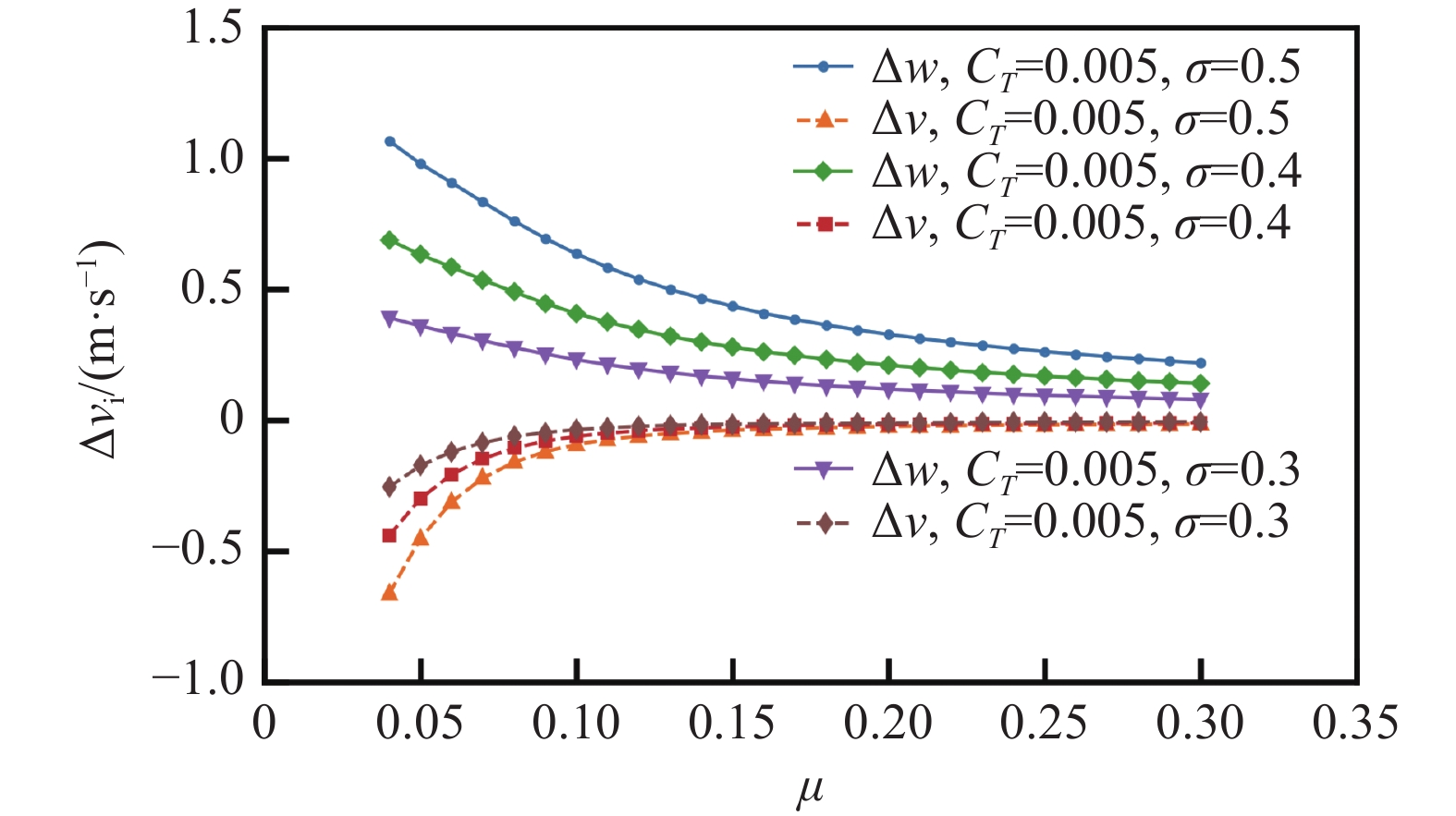
3.2 旋翼模型尺度的影响

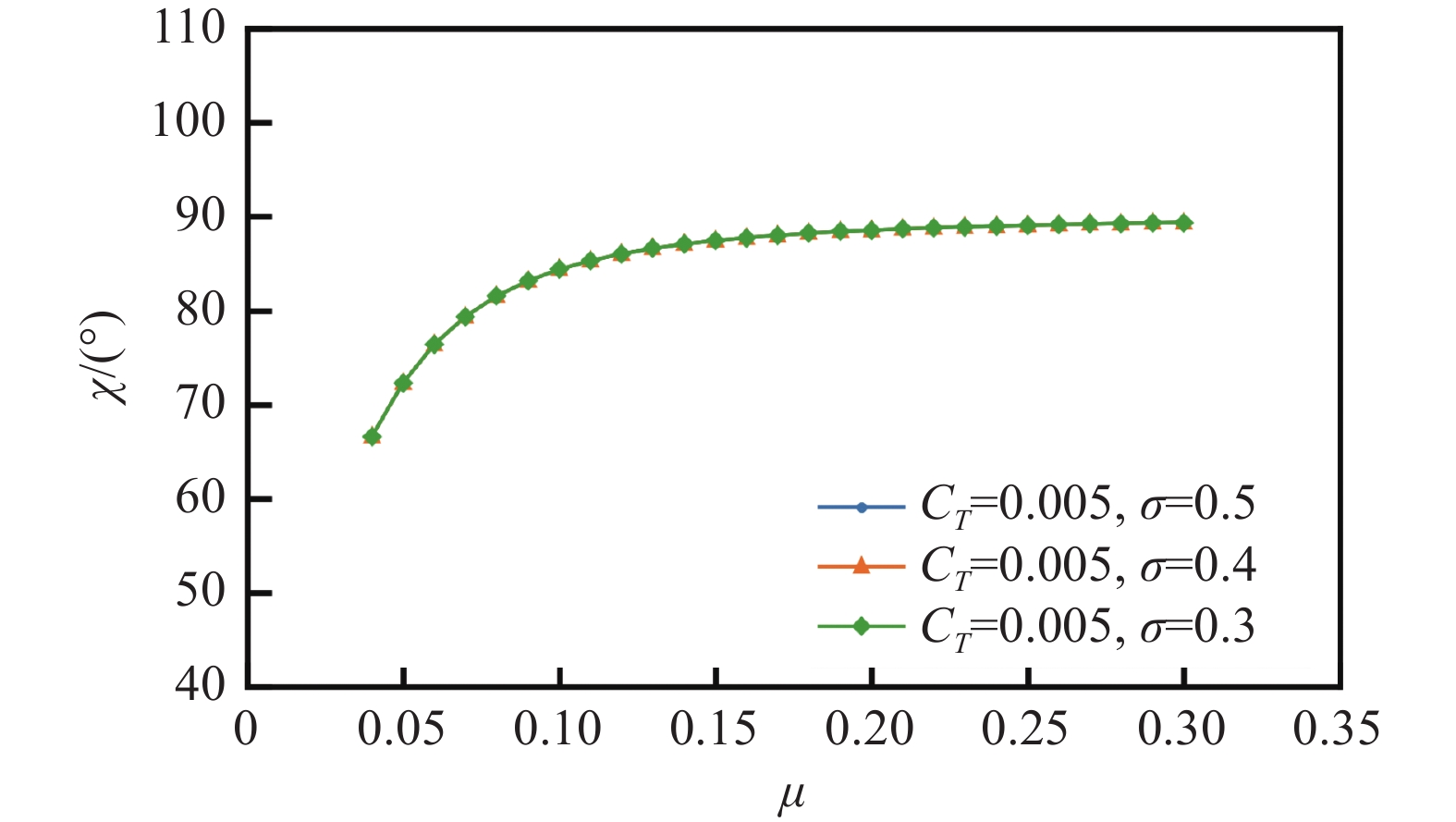
以 $\sigma = R/B$ （R为旋翼半径）评价模型尺度对洞壁干扰的影响，图10、图11、图12分别为相同拉力系数下旋翼模型尺度对尾流偏斜角、修正角和垂向及流向干扰速度的影响。从图10可以看出：相同拉力系数及前进比情况下，模型尺度对尾流偏斜角无影响。其原因由式（5～7）可知：尾流偏斜角χ与风洞来流风速v、桨盘迎角α、拉力系数C_T、桨尖速度v_t有关，旋翼试验不同模型尺度桨尖速度、拉力系数、前进比应保持一致，所以尾流偏斜角与模型尺度无关。

图 10 不同模型尺度尾流偏斜角随前进比变化

Figure 10. The variations of the wake deflection angle with the advance ratio under different rotor model scales

下载: 全尺寸图片幻灯片

图 11 不同模型尺度修正角随前进比变化

Figure 11. The variations of the corrected angle with the advance ratio under different rotor model scales

下载: 全尺寸图片幻灯片

$\chi = \arctan \left(\frac{{{{\text{π}} ^2}}}{4}\frac{{v + {v_{\mathrm{i}}}\sin ( - \alpha )}}{{{v_{\mathrm{i}}}\cos \alpha }}\right)$

(5)

${\left(\frac{{{v_{\mathrm{i}}}}}{{{v_{\mathrm{h}}}}}\right)^4} = \dfrac{1}{{1 - 2\dfrac{v}{{{v_{\mathrm{i}}}}}\sin \alpha + {{\left(\dfrac{v}{{{v_{\mathrm{i}}}}}\right)}^2}}}$

(6)

$v_{\mathrm{h}}^2 = \frac{{{C_T}{{v_{\mathrm{t}}}^2}}}{2}$

(7)

式中：v_i为前飞诱导速度；v_h为对应的悬停诱导速度； $v_{\mathrm{t}}=\omega R,\; \omega$ 为旋翼旋转角速度。

图 12 不同模型尺度干扰速度随前进比变化

Figure 12. The variations of the interference velocity with the advance ratio under different rotor model scales

下载: 全尺寸图片幻灯片

从图11可知，相同前进比下，模型尺度越大，修正角越大。其原因可由图12分析得到：垂向干扰速度随模型尺度增大而逐渐增大，相应的修正角也越大，从而洞壁干扰也越大。这说明不能简单地从尾流偏斜角的大小判断洞壁干扰影响的大小。

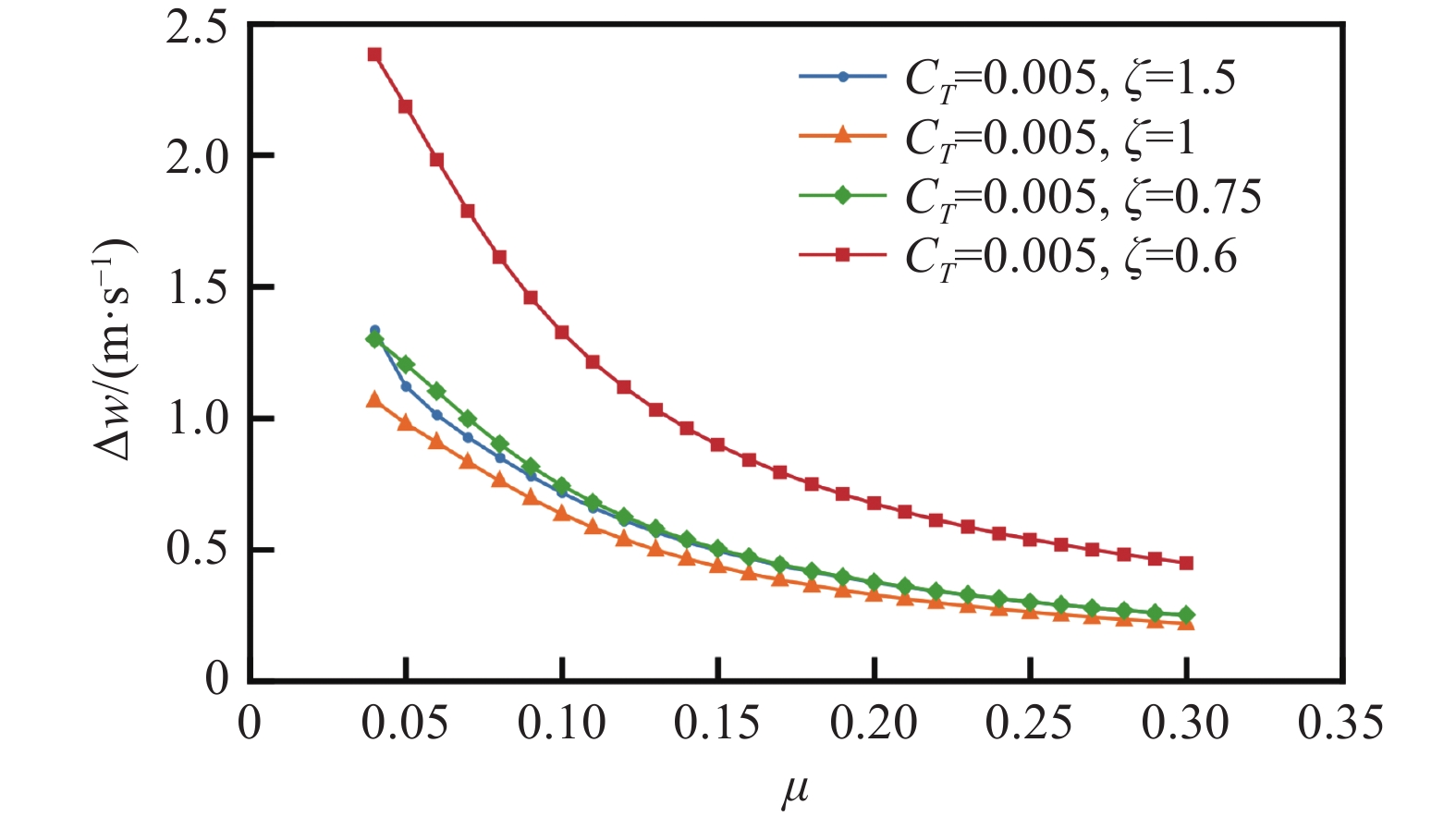
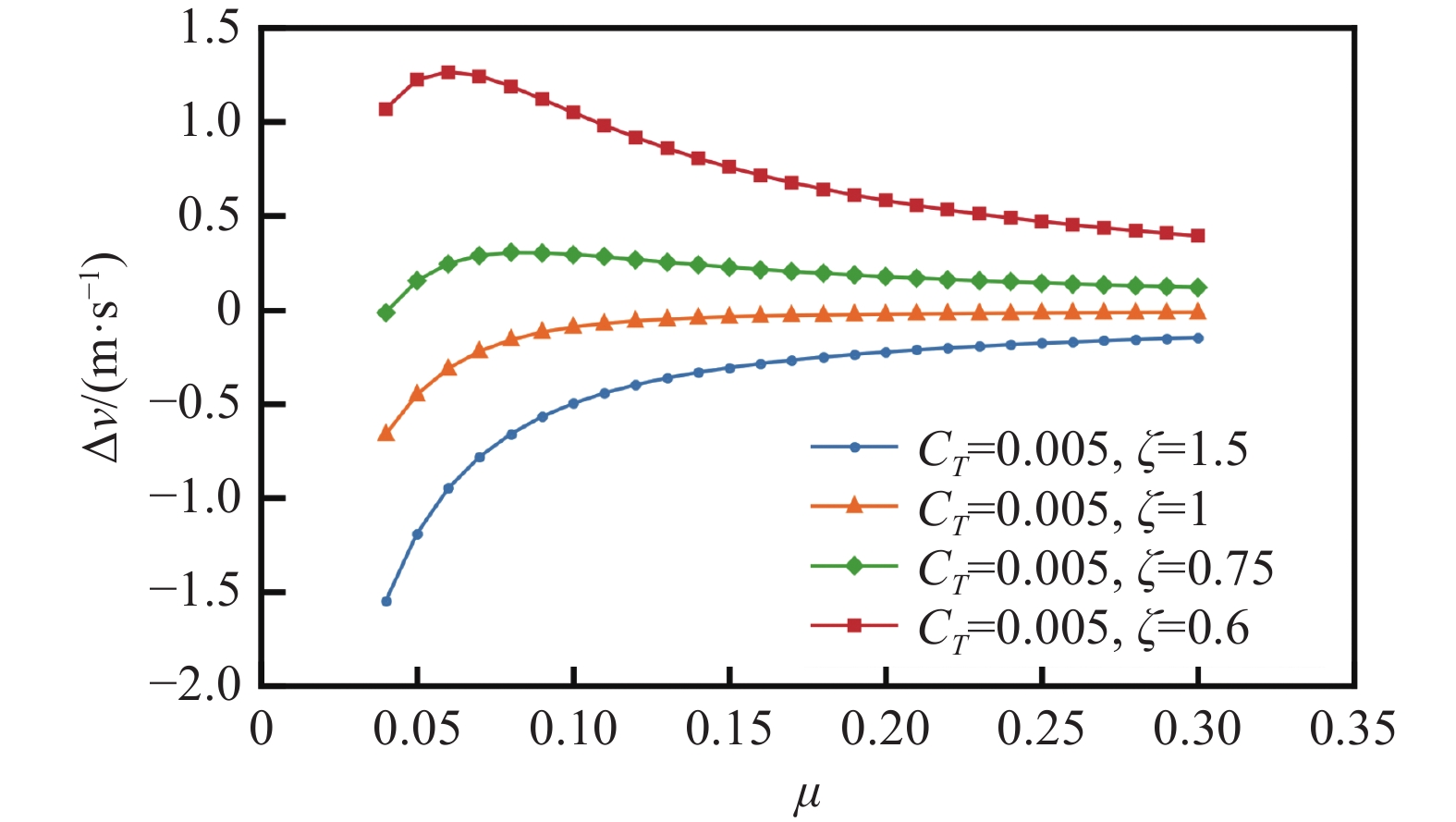
3.3 桨毂中心垂向位置的影响

以 $\zeta = H/h$ 评价桨毂中心垂向位置对洞壁干扰的影响，图13、图14、图15分别为桨毂中心垂向位置对垂向及流向干扰速度和修正角的影响，从这3幅图中可以看出：修正角随着桨毂中心垂向位置先减小后增大，ζ为1时，即桨毂中心位于风洞中心时，垂向干扰速度最小，相应的修正角也最小。因此，旋翼风洞试验时，应尽量使旋翼桨毂中心始终处于风洞中心以减小洞壁干扰。从图13还可以看出，ζ小于1时，即桨毂中心位于风洞中心上方时，流向干扰速度大于0，表现为风速增加，其原因是桨盘靠近上壁面，来流流道减小导致产生类似“固体阻塞”效应，使气流加速；而ζ大于1时，即桨毂中心位于风洞中心下方时，流向干扰速度小于0，表现为风速减小，这是因为“滑流阻塞”效应使旋翼尾流区外速度减小。

图 13 不同桨毂中心垂向位置下垂向干扰速度随前进比的变化

Figure 13. The variations of the vertical interference velocity with the advance ratio under different vertical locations of the hub center

下载: 全尺寸图片幻灯片

图 14 不同桨毂中心垂向位置下流向干扰速度随前进比的变化

Figure 14. The variations of the longitudinal interference velocity with the advance ratio under different vertical locations of the hub center

下载: 全尺寸图片幻灯片

图 15 不同桨毂中心垂向位置下修正角随前进比的变化

Figure 15. The variations of the corrected angle with the advance ratio under different vertical locations of the hub center

下载: 全尺寸图片幻灯片

3.4 风洞开闭口的影响

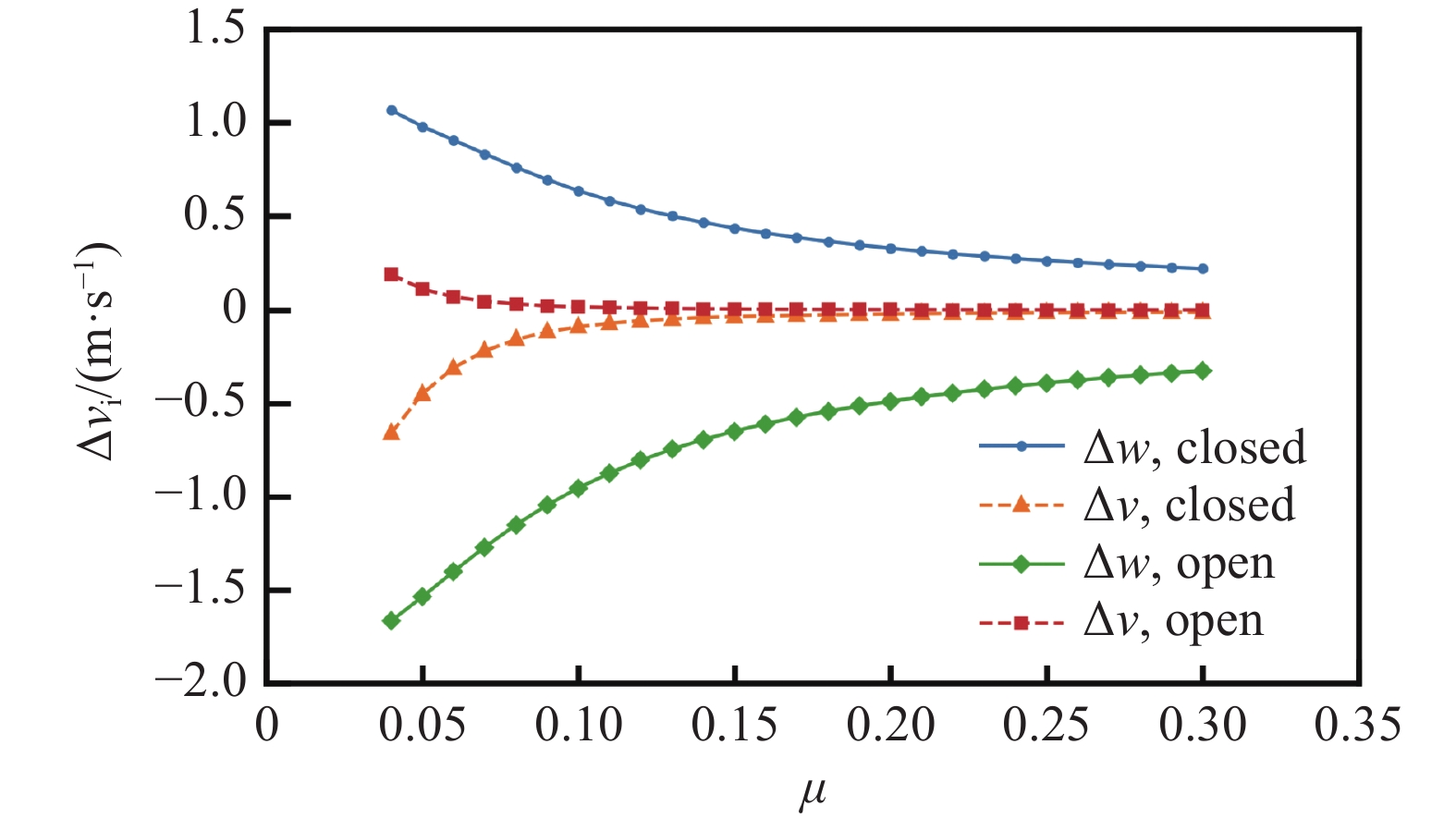
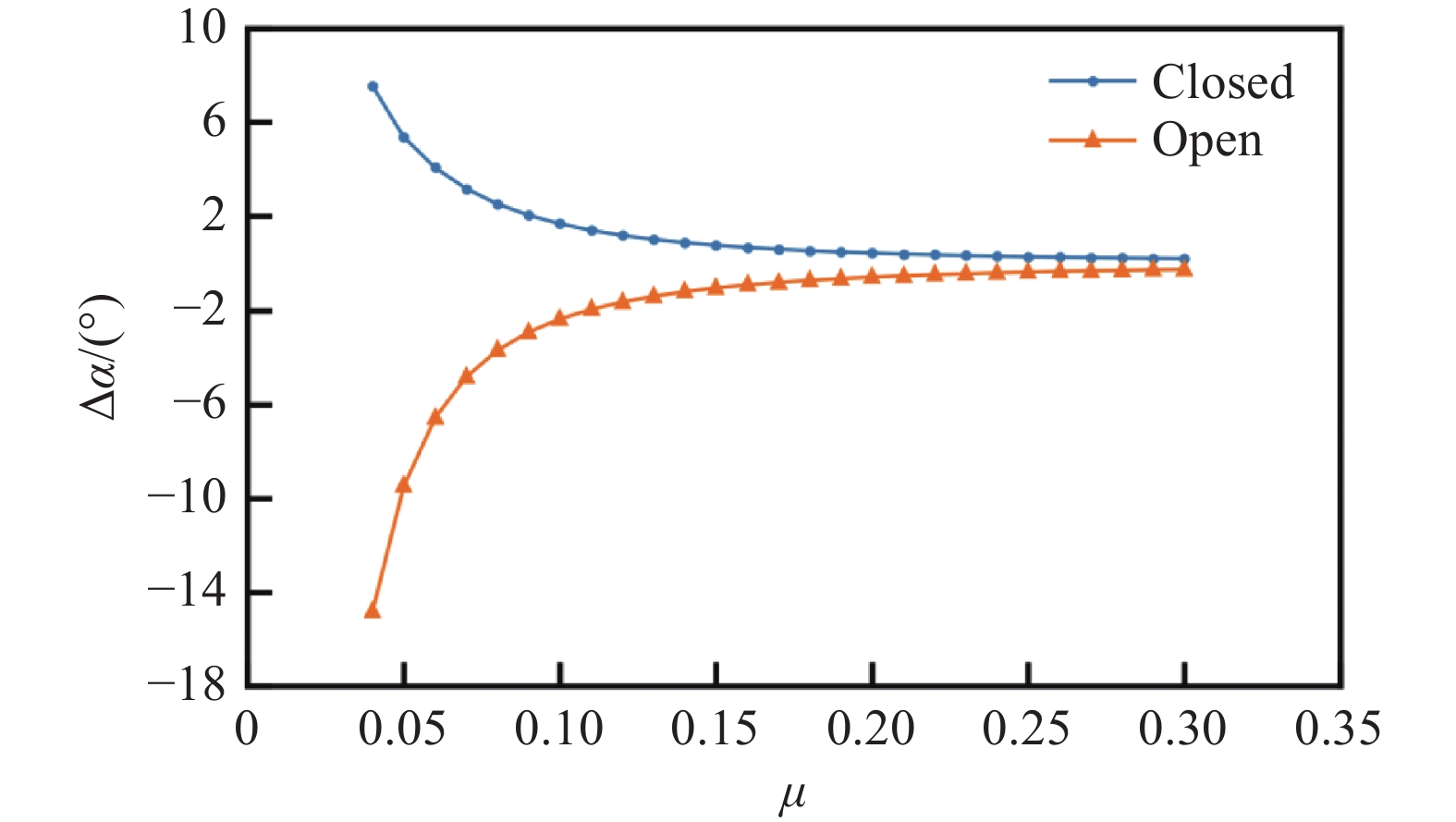
图16、图17分别为相同拉力系数（C_T = 0.005）下风洞开、闭口对垂向及流向干扰速度和修正角的影响，从图中可以看出：相同拉力系数及前进比下，开口风洞干扰速度与闭口形式相反，且垂向干扰速度随前进比变化比流向干扰速度变化大，前进比越小，垂向干扰速度变化越剧烈；风洞开口状态下，垂向干扰速度为负值，这会增大旋翼垂向诱导速度，洞壁对旋翼尾流的干扰作用表现为诱导气流下洗，同时修正角为负值。由于开口时气流不受约束，相同前进比时的垂向干扰速度绝对值比闭口时大，导致修正角绝对值也比闭口时大。

图 16 风洞开闭口形式对干扰速度的影响（C_T = 0.005）

Figure 16. The effects of open/closed wind tunnel on the interference velocity (C_T = 0.005)

下载: 全尺寸图片幻灯片

图 17 风洞开闭口形式对修正角的影响（C_T = 0.005）

Figure 17. The effects of open/closed wind tunnel on the corrected angle (C_T = 0.005)

下载: 全尺寸图片幻灯片

4. 旋翼洞壁干扰参数灵敏度分析

4.1 Sobol灵敏度分析方法

Sobol灵敏度分析方法是一种基于方差的全局灵敏度分析方法，与其他灵敏度分析方法相比，该方法具有全局性、准确性高、能够评估交互效应等优势。其核心思想是将函数f(x)方差分解为单个参数方差和参数之间相互组合的方差，具体表示为：

$\begin{split} f(x)=&f_0+\sum_{i=1}^n f_i\left(x_i\right)+\sum_{1 \leqslant i < j \leqslant n}^n f_{i, j}\left(x_i, x_j\right)+\cdots+ \\ & f_{1,2, \cdots, n}\left(x_1, x_2, \cdots, x_n\right)\\ =&f_0+\sum_{j=1}^{2 n-1} f_{p j}\left(x_{p j}\right) \end{split}$

(8)

式中， ${f_0}$ 为常数项，x=(x_1，x₂，···x_n)为自变量，定义域Kⁿ={(x_1，x₂，···x_n)|0≤x_i≤1,i=1,2, ···,n}， ${f_{pj}}$ 为子函数，各子函数正交且在定义域内积分为0，则有：

$\left\{ \begin{array}{l} {f_0} = \displaystyle\int_K {f(x)} {\mathrm{d}}x \\ {f_i}({x_i}) = \displaystyle\int_{{K^{n - 1}}} {f(x)} {\mathrm{d}}{x^i} - {f_0} \\ {f_{ij}}({x_i},{x_j}) = \displaystyle\int_{{K^{n - 2}}} {f(x)} {\mathrm{d}}{x^{ij}} - {f_i}({x_i}) - {f_j}({x_j}) - {f_0} \\ \vdots \end{array} \right.$

(9)

式中， ${\rm{d}}{x^i}$ 、 ${\rm{d}}{x^{ij}}$ 分别为 ${\rm{d}}{x_1},{\rm{d}}{x_2}, \cdots ,{\rm{d}}{x_n}$ 中不含 ${\rm{d}}{x^i}$ 、 ${\rm{d}}{x_i}{\rm{d}}{x_j}$ 的乘积，K^n-1、K^n-2分别为不含x_i和x_i、x_j的定义域。则函数的偏方差和总方差为：

$\left\{\begin{array}{l} {V_i} = \displaystyle\int {{f^2}({x_i})} {\rm{d}}{x_i} \\ {V_{ij}} = \displaystyle\int {{f^2}({x_i},{x_j})} {\rm{d}}{x_i}{\rm{d}}{x_j} \\ V = \displaystyle\int {{f^2}(x)} {\mathrm{d}}x \end{array} \right.$

(10)

灵敏度系数可表示为：

$\left\{ \begin{array}{l} {S_{1i}} = \dfrac{{{V_i}}}{V} \\ {S_{2ij}} = \dfrac{{{V_{ij}}}}{V} \\ {S_{{\text{T}}i}} = \dfrac{{V - {V_{\sim i}}}}{V} \end{array} \right.$

(11)

其中， ${V_{\sim i}}$ 为除了参数x_i之外的其余参数的方差， ${S_{1i}}$ 为参数x_i的一阶灵敏度系数， ${S_{2ij}}$ 为参数x_i和x_j交互影响的二阶灵敏度系数， ${S_{{\text{T}}i}}$ 为参数x_i的总灵敏度系数。

4.2 旋翼洞壁干扰灵敏度分析

采用Sobol方法对洞壁干扰进行参数灵敏度分析，各影响参数取值范围如表3所示。

表 3 各影响参数取值范围

Table 3. Value range of each impact parameter

参数	取值范围
ζ	0.6～1.5
C_T	0.001～0.005
μ	0.04～0.30
σ	0.30～0.65
$\alpha_{\mathrm{s}}$	–10°～5°

下载: 导出CSV

| 显示表格

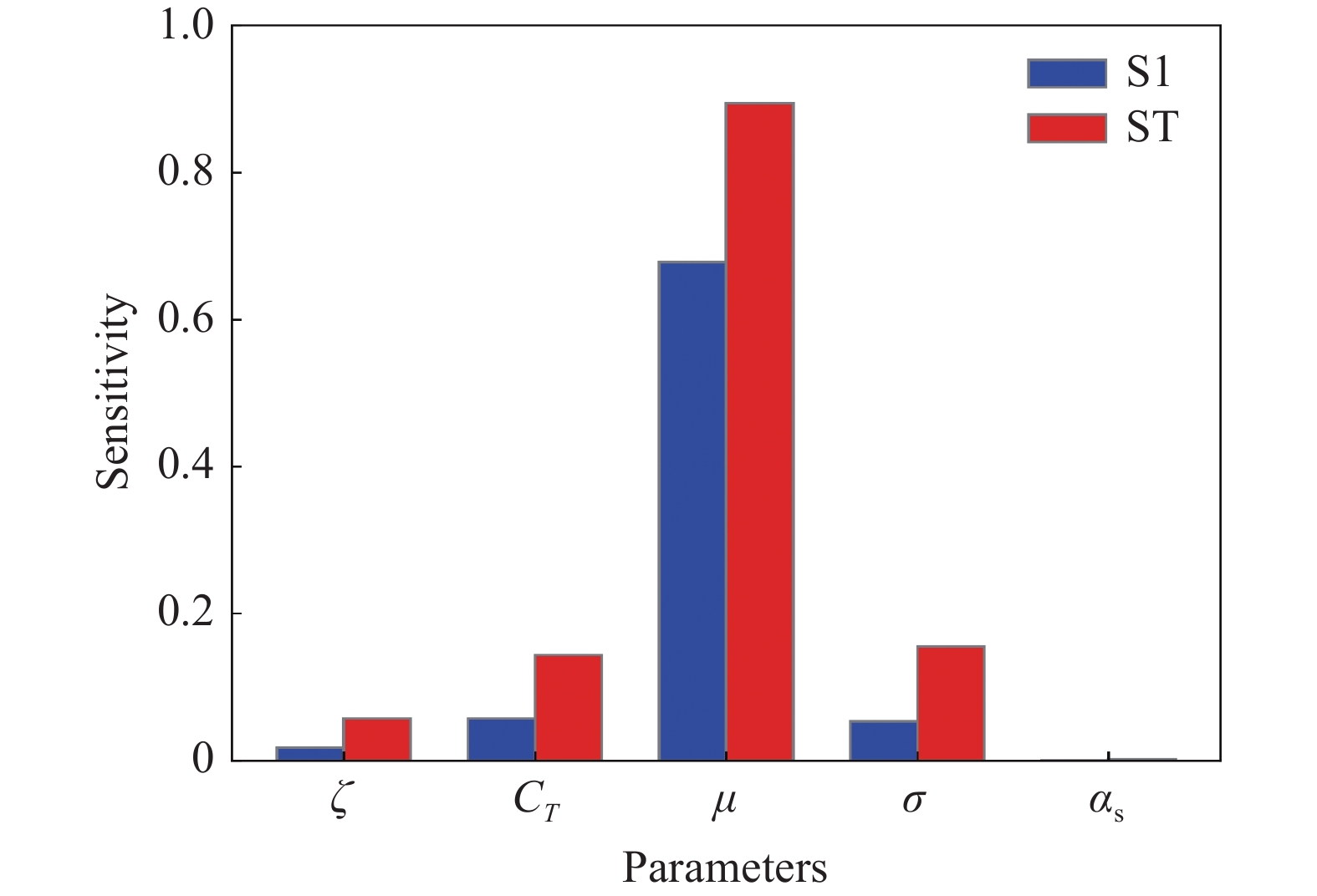
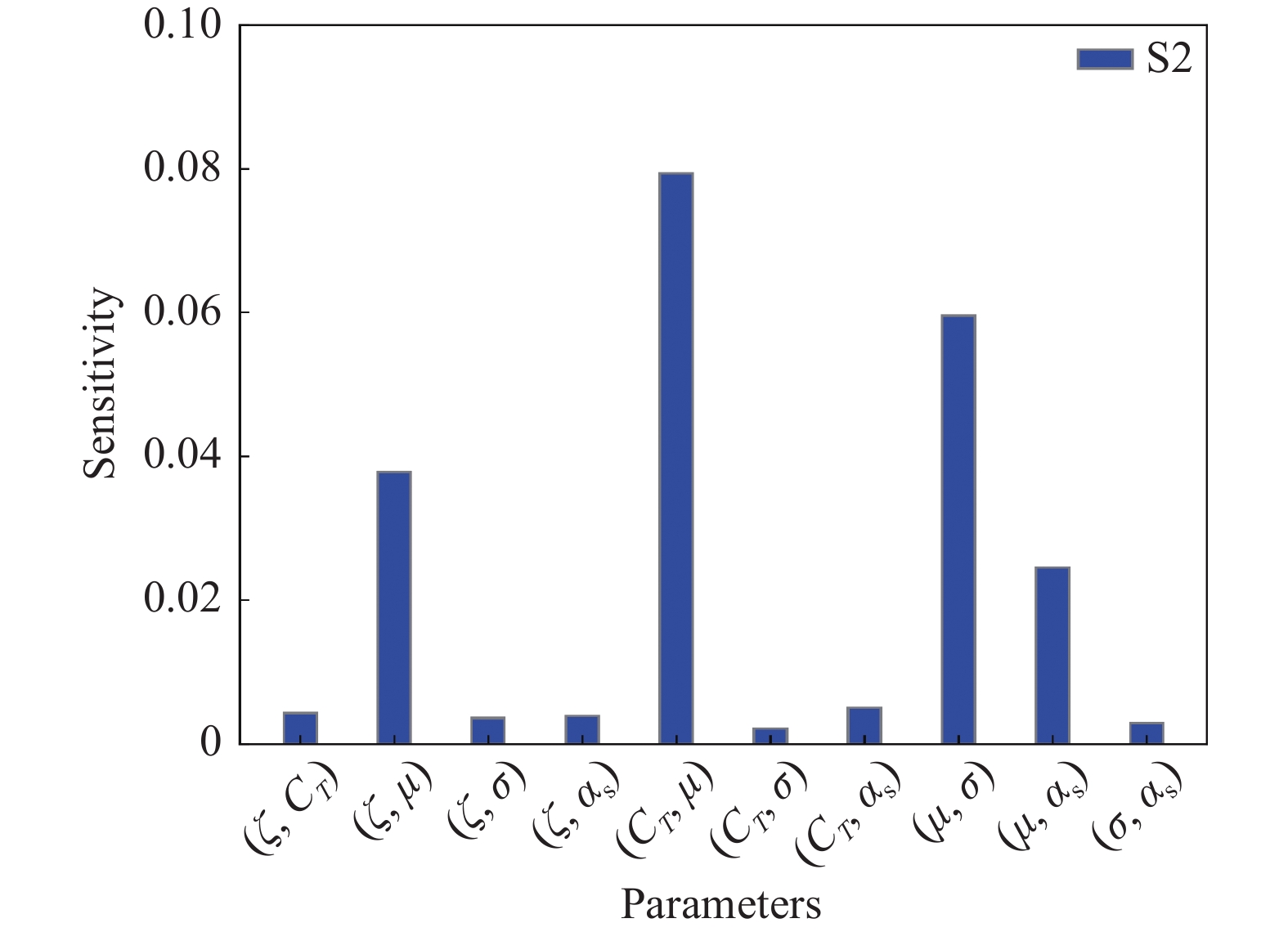
采用Sobol序列法在参数取值空间采样，共24576个样本点。图18为各影响参数的一阶灵敏度和总灵敏度，图19为各影响参数的二阶灵敏度。一阶灵敏度S1表示一个变量单独变化对输出结果的影响；总灵敏度ST不但反应单独参数变化时所产生的影响，还反应与其他参数交互作用产生的影响；二阶灵敏度S2表示两个变量同时变化对输出结果的影响。从图18可以看出：μ的一阶灵敏度达0.678，总灵敏度达0.894，是最灵敏的参数，可见其对修正角大小起决定性作用。从图19可以看出：虽然C_T和μ之间、σ和μ之间有较强的交互作用，导致C_T和σ总灵敏度相较于一阶灵敏度有较大增长，但仍小于μ的总灵敏度，利用此特点可以在特定试验状态下对旋翼模型尺度选择进行优化。比如，由于洞壁干扰对前进比最敏感，且大前进比时洞壁干扰较小，所以在开展旋翼大前进比状态气动特性研究时，可以适当增加旋翼模型尺度，进而可在风洞尺寸一定的情况下提升旋翼模型试验雷诺数模拟能力。

图 18 各影响参数的一阶灵敏度和总灵敏度直方图

Figure 18. Histogram of the first-order and total sensitivity of each influence parameter

下载: 全尺寸图片幻灯片

图 19 各影响参数的二阶灵敏度直方图

Figure 19. Histogram of the second-order sensitivity ofeach influence parameter

下载: 全尺寸图片幻灯片

5. 结　论

本文基于Heyson方法构建了旋翼洞壁干扰修正方法并验证，基于此方法分析了洞壁干扰参数影响机理，计算了各参数对洞壁干扰的灵敏度。具体结论为：

1）桨毂中心越靠近风洞中心，洞壁干扰相对越小，桨毂中心升高和降低都不能减小洞壁干扰。

2）闭口风洞和开口风洞洞壁干扰分别表现为诱导上洗和诱导下洗，且开口洞壁干扰量大于闭口。

3）洞壁干扰对前进比最为敏感，拉力系数和旋翼模型尺度为次要影响参数。

4）开展大前进比旋翼特性研究时，可适当增大模型尺度以提升试验雷诺数。

本文基于经典洞壁干扰修正方法开展洞壁干扰参数灵敏度分析，并指出为进一步提高洞壁干扰修正及灵敏度分析准度，可开展旋翼洞壁干扰创新方法研究，并发展复杂旋翼飞行器洞壁干扰修正模型。

图 18 各影响参数的一阶灵敏度和总灵敏度直方图

Figure 18. Histogram of the first-order and total sensitivity of each influence parameter

下载: 全尺寸图片幻灯片

图 1 不同风洞形式映像系统

Figure 1. Image systems of different wind tunnel configurations

下载: 全尺寸图片幻灯片

图 2 旋翼桨盘控制点分布

Figure 2. Distribution of control points on the rotor disk

下载: 全尺寸图片幻灯片

图 3 在FL-10风洞开、闭口试验段中的旋翼模型

Figure 3. Rotor model set-up in the open and closed test sections of the FL-10 wind tunnel

下载: 全尺寸图片幻灯片

图 4 开、闭口试验修正前后的主轴倾角对比

Figure 4. Comparison of the rotor main shaft tilt angles in the open and closed test sections before and after correction

下载: 全尺寸图片幻灯片

图 5 不同前进比下功率系数随主轴倾角的变化

Figure 5. The variations of the power coefficient with the shaft tilt angle under different advance ratios

下载: 全尺寸图片幻灯片

图 6 开、闭口试验修正前后的功率系数与前进比关系对比

Figure 6. Comparison of the relationship between the power coefficient and the advance ratio before and after correction in the open and closed test sections

下载: 全尺寸图片幻灯片

图 7 不同拉力系数下尾流偏斜角随前进比变化

Figure 7. The variations of the wake deflection angle with the advance ratio under different thrust coefficients

下载: 全尺寸图片幻灯片

图 8 不同拉力系数下修正角随前进比变化

Figure 8. The variations of the corrected angle with the advance ratio under different thrust coefficients

下载: 全尺寸图片幻灯片

图 9 不同拉力系数下干扰速度随前进比变化

Figure 9. The variations of the interference velocity with the advance ratio under different thrust coefficients

下载: 全尺寸图片幻灯片

图 10 不同模型尺度尾流偏斜角随前进比变化

Figure 10. The variations of the wake deflection angle with the advance ratio under different rotor model scales

下载: 全尺寸图片幻灯片

图 11 不同模型尺度修正角随前进比变化

Figure 11. The variations of the corrected angle with the advance ratio under different rotor model scales

下载: 全尺寸图片幻灯片

图 12 不同模型尺度干扰速度随前进比变化

Figure 12. The variations of the interference velocity with the advance ratio under different rotor model scales

下载: 全尺寸图片幻灯片

图 13 不同桨毂中心垂向位置下垂向干扰速度随前进比的变化

Figure 13. The variations of the vertical interference velocity with the advance ratio under different vertical locations of the hub center

下载: 全尺寸图片幻灯片

图 14 不同桨毂中心垂向位置下流向干扰速度随前进比的变化

Figure 14. The variations of the longitudinal interference velocity with the advance ratio under different vertical locations of the hub center

下载: 全尺寸图片幻灯片

图 15 不同桨毂中心垂向位置下修正角随前进比的变化

Figure 15. The variations of the corrected angle with the advance ratio under different vertical locations of the hub center

下载: 全尺寸图片幻灯片

图 16 风洞开闭口形式对干扰速度的影响（C_T = 0.005）

Figure 16. The effects of open/closed wind tunnel on the interference velocity (C_T = 0.005)

下载: 全尺寸图片幻灯片

图 17 风洞开闭口形式对修正角的影响（C_T = 0.005）

Figure 17. The effects of open/closed wind tunnel on the corrected angle (C_T = 0.005)

下载: 全尺寸图片幻灯片

图 19 各影响参数的二阶灵敏度直方图

Figure 19. Histogram of the second-order sensitivity ofeach influence parameter

下载: 全尺寸图片幻灯片

表 1 不同风洞形式p、q、s取值

Table 1 Values of p, q, s with different wind tunnelconfigurations

风洞形式	洞壁干扰因子	p	q	s
闭口	${\delta _{w,{\rm{L}}}}$	0	0	0
	${\delta _{v,{\rm{L}}}}$	0	1	0
	${\delta _{w,{\rm{D}}}}$	0	0	1
	${\delta _{v,{\rm{D}}}}$	0	1	1

开口	${\delta _{w,{\rm{L}}}}$	m	1	1
	${\delta _{v,{\rm{L}}}}$	m	0	1
	${\delta _{w,{\rm{D}}}}$	m	1	0
	${\delta _{v,{\rm{D}}}}$	m	0	0

下载: 导出CSV

表 2 风洞试验状态

Table 2 Test conditions in the wind tunnel

μ	$\alpha_{\mathrm{s}}$ /(°)	C_w	${{Ma}}_{\mathrm{T}}$
0.059	–1.6	0.005	0.641
0.096	–2.2	0.005	0.641
0.136	–2.9	0.005	0.641
0.173	–3.9	0.005	0.641
0.227	–5.7	0.005	0.641
0.273	–7.7	0.005	0.641

下载: 导出CSV

表 3 各影响参数取值范围

Table 3 Value range of each impact parameter

参数	取值范围
ζ	0.6～1.5
C_T	0.001～0.005
μ	0.04～0.30
σ	0.30～0.65
$\alpha_{\mathrm{s}}$	–10°～5°

下载: 导出CSV

参考文献(30)

[1]	GLAUERT H. The interference on the characteristics of an airfoil in a wind tunnel of rectangular section: ARC-RM-1459[R]. Great Britain Aeronautical Research Council, 1932.
[2]	HEYSON H H. Linearized theory of wind-tunnel jet-boundary corrections and ground effect for VTOL-STOL aircraft: NASA TR-R-124 [R]. NASA, 1962.
[3]	HEYSON H H. FORTRAN programs for calculating wind-tunnel boundary interference: NASA TM X-1740 [R]. NASA, 1969.
[4]	HEYSON H H. Use of superposition in digital computers to obtain wind tunnel interference factors for arbitrary configurations, with particular reference to V/STOL models: NASA TR R-302 [R]. NASA, 1969.
[5]	杨永东, 袁红刚, 黄明其, 等. CARDC的直升机气动力试验研究新进展[J]. 直升机技术, 2008(3): 129−134. doi: 10.3969/j.issn.1673-1220.2008.03.023 YANG Y D, YUAN H G, HUANG M Q, et al. Recent progresses of helicopter aerodynamic test and research at CARDC[J]. Helicopter Technique, 2008(3): 129−134(in Chinese). doi: 10.3969/j.issn.1673-1220.2008.03.023
[6]	GOULDING P W, NYKAMP C M, BARTOW B B. Developing a wall interference effects correction technique for high-lift and rotor configurations in the national full-scale aerodynamics complex[C]// 55th AIAA Aerospace Sciences Meeting, Grapevine, Texas. AIAA, 2017: AIAA 2017-0485.
[7]	GOULDING P W, NYKAMP C M, BARTOW B B. Assessing wall interference effects on a medium-sized rotor in the national full-scale aerodynamics complex[C]// 55th AIAA Aerospace Sciences Meeting, Grapevine, Texas. AIAA, 2017: AIAA 2017-0773.
[8]	KOLAEI A, BARCELOS D, BRAMESFELD G. Experimental analysis of a small‐scale rotor at various inflow angles[J]. International Journal of Aerospace Engineering, 2018(1): 2560370. doi: 10.1155/2018/2560370
[9]	BEAUMIER P, PRIEUR J, SPIEGEL P, et al. Effect of higher harmonic control on helicopter rotor blade-vortex interaction noise: Prediction and initial validation: 96N13608[R]. NASA, 1995.
[10]	LANGER H J, PETERSON R L, MAIER T H. An experimental evaluation of wind tunnel wall correction methods for helicopter performance[C]// American Helicopter Society 52nd Annual Forum, Washington, DC., 1996.
[11]	SHINODA P M. Wall interaction effects for a full-scale helicopter rotor in the NASA Ames 80- by 120-foot wind tunnel: 95N19270[R]. NASA, 1994.
[12]	何瑞恒. 直升机模型风洞试验洞壁干扰修正方法研究[D]. 南京: 南京航空航天大学, 2012. HE R H. Study on correction method of tunnel wall interference in helicopter model wind tunnel test[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012 (in Chinese).
[13]	BIAVA M, VIGEVANO L. Simulation of a complete helicopter: A CFD approach to the study of interference effects[J]. Aerospace Science and Technology, 2012, 19(1): 37−49. doi: 10.1016/j.ast.2011.08.006
[14]	BIAVA M, VIGEVANO L. Computational assessment of wind tunnel flow in closed and open section model rotor tests[J]. Journal of the American Helicopter Society, 2014, 59(1): 1−17. doi: 10.4050/jahs.59.012006
[15]	BIAVA M, VALENTINI M, VIGEVANO L. Wind tunnel corrections for isolated rotor tests[C]// 39th European Rotorcraft Forum, Moscow, Russia, 2013: 1−11.
[16]	BIAVA M, BONIFACE J, VIGEVANO L. Influence of wind-tunnel walls in helicopter aerodynamics predictions[C]// 31st European Rotorcraft Forum, Florence, Italy, 2005: 1−10.
[17]	BIAVA M, THOMOPOULOS A, VIGEVANO L. Computational assessment of flow breakdown in closed section model rotor tests[C]// 37th European Rotorcraft Forum, Gallarate, Italy, 2011: 708−717.
[18]	BOFFADOSSI M, VALENTINI M, VIGEVANO L. Shaft angle corrections for rotor tests in a closed section wind tunnel[C]// 40th European Rotorcraft Forum, 2014: 700−711.
[19]	KONING W J F. Wind tunnel interference effects on tilt rotor testing using computational fluid dynamics: ARC-E-DAA-TN27721 [R]. NASA, 2016.
[20]	GAROFANO-SOLDADO A, HEREDIA G, OLLERO A. Aerodynamic interference in confined environments with tilted propellers: wall effect and corner effect[C]//Proc of the 2021 Aerial Robotic Systems Physically Interacting with the Environment (AIRPHARO), Biograd na Moru, Croatia. IEEE, 2021: 1−8.
[21]	PETERSON R L, MAIER T, COMMAND T, et al. Correlation of wind tunnel and flight test results of a full-scale hingeless rotor[C]//Proceedings of the American Helicopter Society Aeromechanics Specialist Conference, San Francisco, CA, 1994.
[22]	TAN J F, CAI J G, BARAKOS G N, et al. Computational study on the aerodynamic interference between tandem rotors and nearby obstacles[J]. Journal of Aircraft, 2020, 57(3): 456−468. doi: 10.2514/1.c035629
[23]	QUACKENBUSH T R, WHITEHOUSE G R, YU M K. Analysis of rotor/airframe interaction in hover and near-hover flight conditions[C]//Proc of the AIAA Scitech 2019 Forum, San Diego, California. AIAA, 2019: AIAA 2019-0596.
[24]	BORGONOVO E, PLISCHKE E. Sensitivity analysis: A review of recent advances[J]. European Journal of Operational Research, 2016, 248(3): 869−887. doi: 10.1016/j.ejor.2015.06.032
[25]	宋健, 佘湖清, 李超, 等. 基于Sobol'灵敏度分析的火箭弹自力弹射多目标约束优化[J]. 推进技术, 2022, 43(12): 40−48. doi: 10.13675/j.cnki.tjjs.210833 SONG J, SHE H Q, LI C, et al. Multi-object constraint optimization of rocket self-ejection based on Sobol' sensitivity analysis[J]. Journal of Propulsion Technology, 2022, 43(12): 40−48(in Chinese). doi: 10.13675/j.cnki.tjjs.210833
[26]	田世超, 杜新, 武猛, 等. 吸气式巡航飞行器气动设计参数灵敏度分析[J]. 战术导弹技术, 2020(3): 8−15. doi: 10.16358/j.issn.1009-1300.2020.9.154 TIAN S C, DU X, WU M, et al. Sensitivity analysis of air-breathing cruise vehicle aerodynamic design parameters[J]. Tactical Missile Technology, 2020(3): 8−15(in Chinese). doi: 10.16358/j.issn.1009-1300.2020.9.154
[27]	WALKER E, EVERHART J, IYER V. Sensitivity study of the wall interference correction system (WICS) for rectangular tunnels[C]// 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. AIAA, 2001: AIAA 2001-159.
[28]	WALKER E, EVERHART J, IYER V. Parameter sensitivity study of the wall interference correction system (WICS)[C]// 19th AIAA Applied Aerodynamics Conference, Anaheim, CA, USA. AIAA, 2001: AIAA 2001−2421.
[29]	TAI M, HWANG H, JEONG S, et al. Feasibility study of data-driven wall interference correction framework for subsonic wind tunnel[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2024, 254: 105923. doi: 10.1016/j.jweia.2024.105923
[30]	SOBOL I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathematics and Computers in Simulation, 2001, 55(1-3): 271−280. doi: 10.1016/S0378-4754(00)00270-6

施引文献

资源附件(0)

图(19) / 表(3)

计量

文章访问数: 32
HTML全文浏览量: 1
PDF下载量: 17
被引次数: 0

0. 引　言
1. Heyson洞壁干扰修正方法
2. 旋翼洞壁干扰计算方法验证
2.1 风洞和模型
2.2 试验内容及方法
3. 旋翼洞壁干扰参数影响分析
3.1 拉力系数的影响
3.2 旋翼模型尺度的影响
3.3 桨毂中心垂向位置的影响
3.4 风洞开闭口的影响
4. 旋翼洞壁干扰参数灵敏度分析
4.1 Sobol灵敏度分析方法
4.2 旋翼洞壁干扰灵敏度分析
5. 结　论

0. 引　言
1. Heyson洞壁干扰修正方法
2. 旋翼洞壁干扰计算方法验证
2.1 风洞和模型
2.2 试验内容及方法
3. 旋翼洞壁干扰参数影响分析
3.1 拉力系数的影响
3.2 旋翼模型尺度的影响
3.3 桨毂中心垂向位置的影响
3.4 风洞开闭口的影响
4. 旋翼洞壁干扰参数灵敏度分析
4.1 Sobol灵敏度分析方法
4.2 旋翼洞壁干扰灵敏度分析
5. 结　论

参考文献(30)

施引文献

资源附件(0)

旋翼风洞试验洞壁干扰参数影响及敏感性分析

通讯作者: 刘向楠（1987—），男，内蒙古赤峰人，高级工程师，研究方向：飞行器风洞试验技术. E-mail：liuxiangnan200851@163.com

计量

出版历程

Analysis of impact and sensitivity of wall interference parameters in wind tunnel test of rotors

0. 引 言

1. Heyson洞壁干扰修正方法

2. 旋翼洞壁干扰计算方法验证

2.1 风洞和模型

2.2 试验内容及方法

3. 旋翼洞壁干扰参数影响分析

3.1 拉力系数的影响

3.2 旋翼模型尺度的影响

3.3 桨毂中心垂向位置的影响

3.4 风洞开闭口的影响

4. 旋翼洞壁干扰参数灵敏度分析

4.1 Sobol灵敏度分析方法

4.2 旋翼洞壁干扰灵敏度分析

5. 结 论

计量

出版历程

目录

0. 引 言

1. Heyson洞壁干扰修正方法

2. 旋翼洞壁干扰计算方法验证

2.1 风洞和模型

2.2 试验内容及方法

3. 旋翼洞壁干扰参数影响分析

3.1 拉力系数的影响

3.2 旋翼模型尺度的影响

3.3 桨毂中心垂向位置的影响

3.4 风洞开闭口的影响

4. 旋翼洞壁干扰参数灵敏度分析

4.1 Sobol灵敏度分析方法

4.2 旋翼洞壁干扰灵敏度分析

5. 结 论

通讯作者:
刘向楠（1987—），男，内蒙古赤峰人，高级工程师，研究方向：飞行器风洞试验技术. E-mail：liuxiangnan200851@163.com

0. 引　言

5. 结　论

0. 引　言

5. 结　论