Study on the linear instability of asymmetric streamwise vortices over a high-speed lifting body
-
摘要:
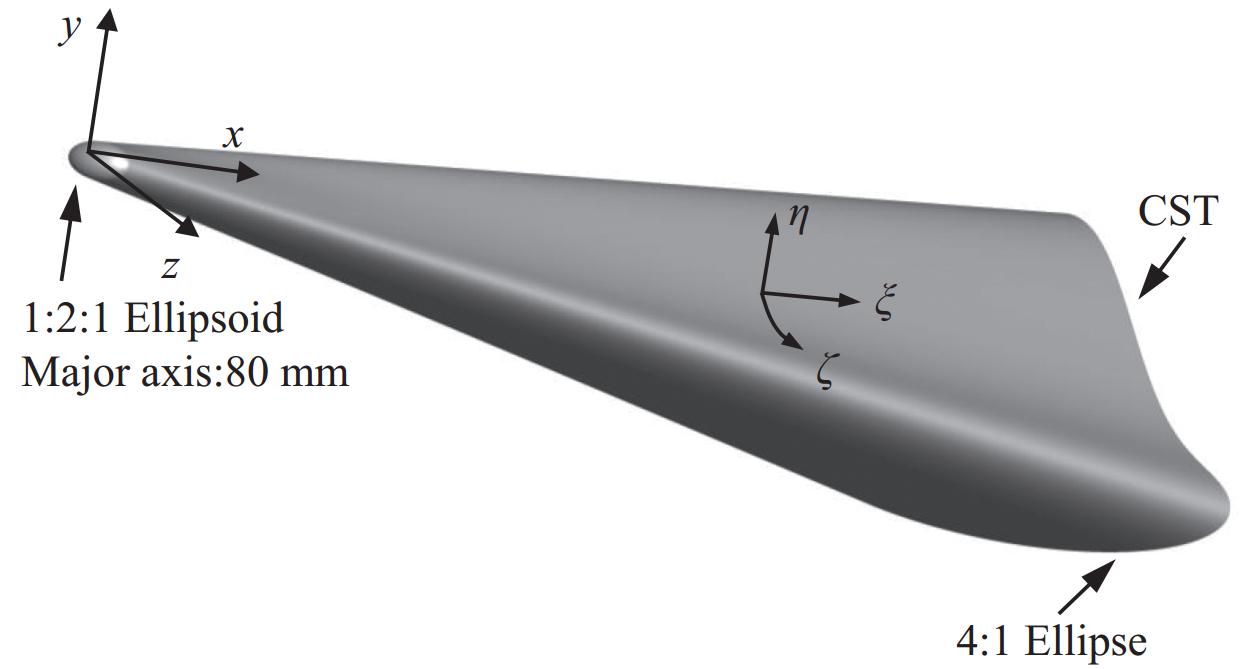
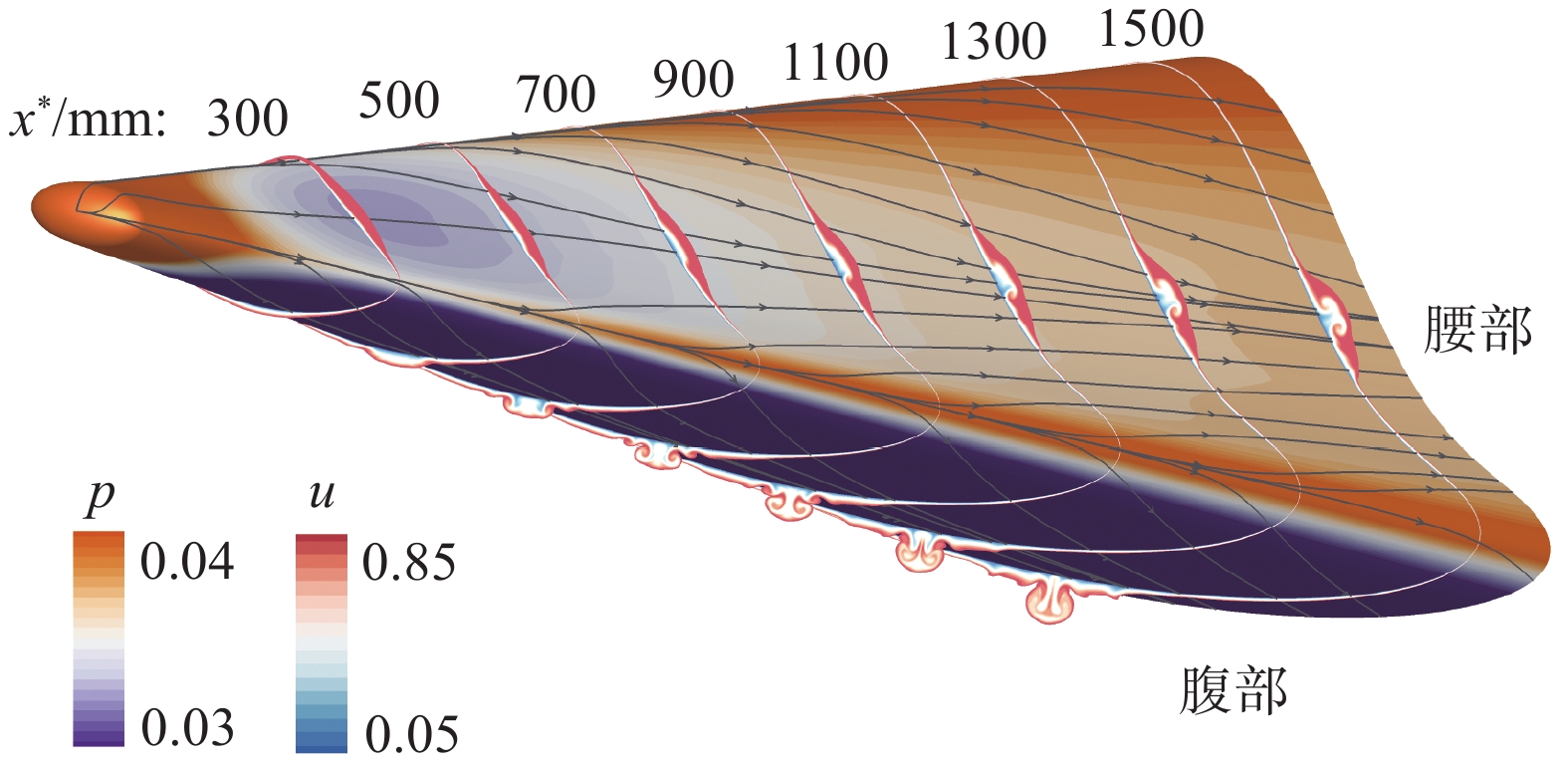
高速飞行器实际飞行时存在非对称流动，为加深对非对称三维流场结构失稳机制的认识，采用二维全局稳定性分析方法对高速转捩研究飞行器（HyTRV）腰部非对称流向涡结构的稳定性特征进行了研究。模型长度为
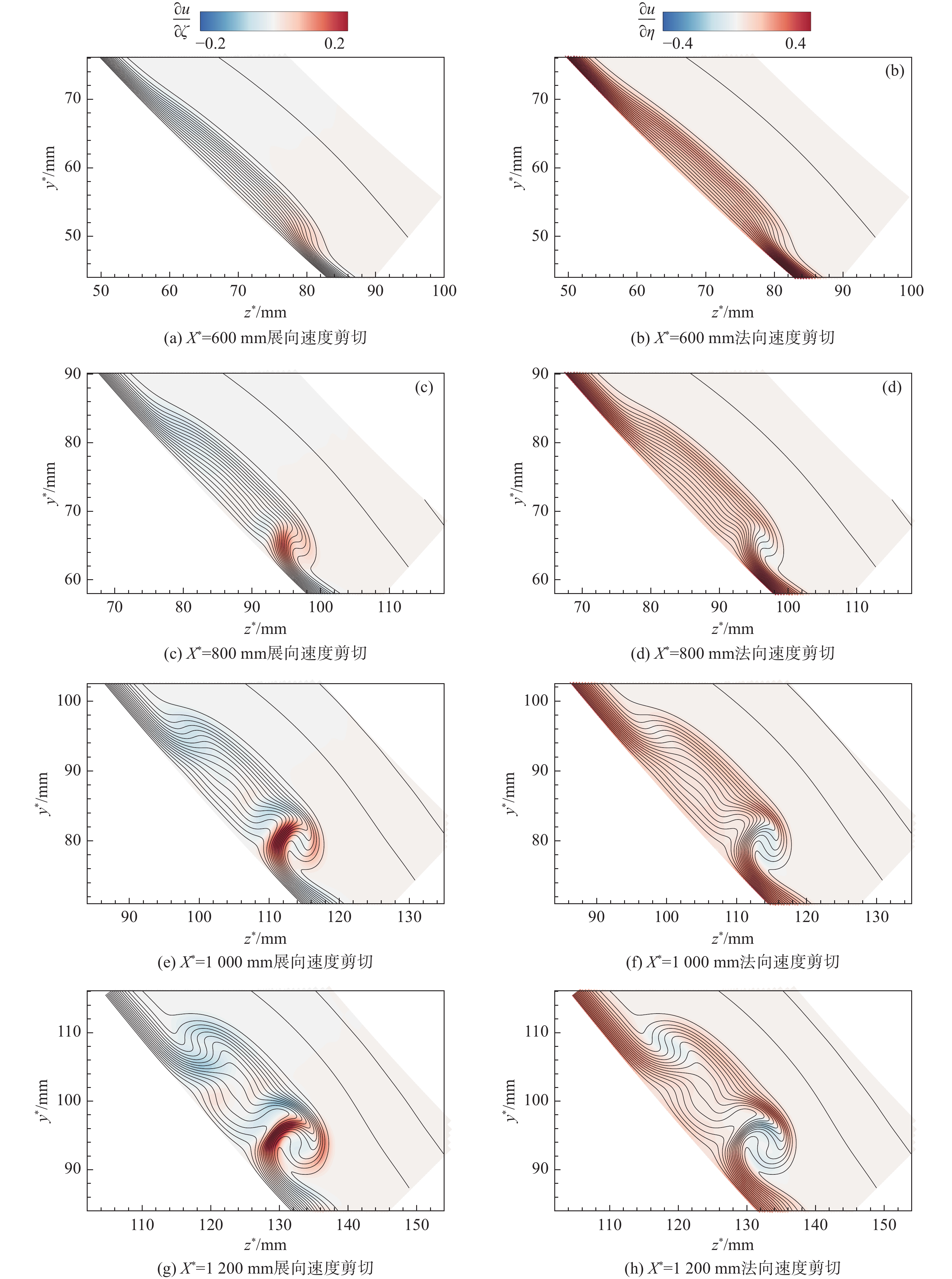
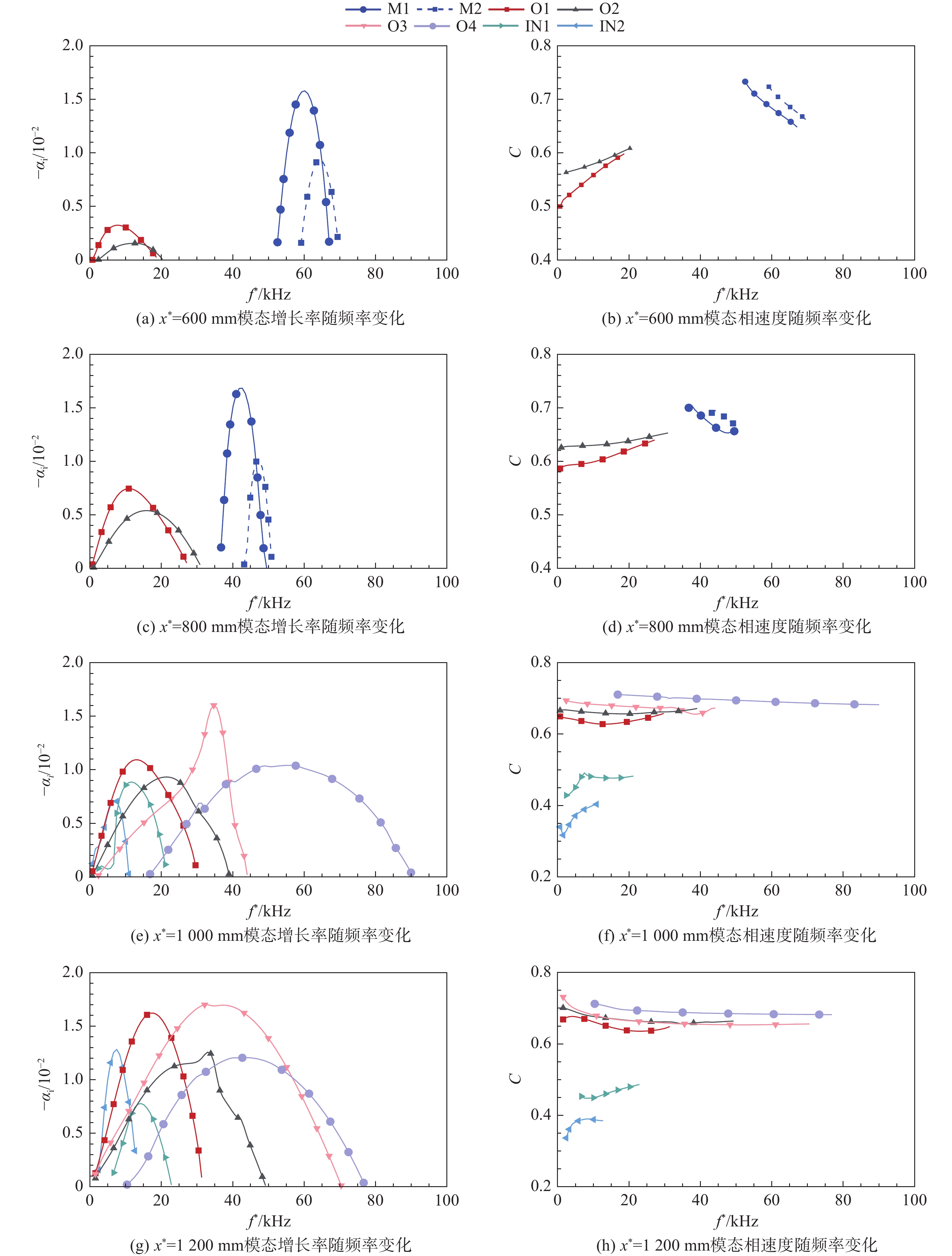
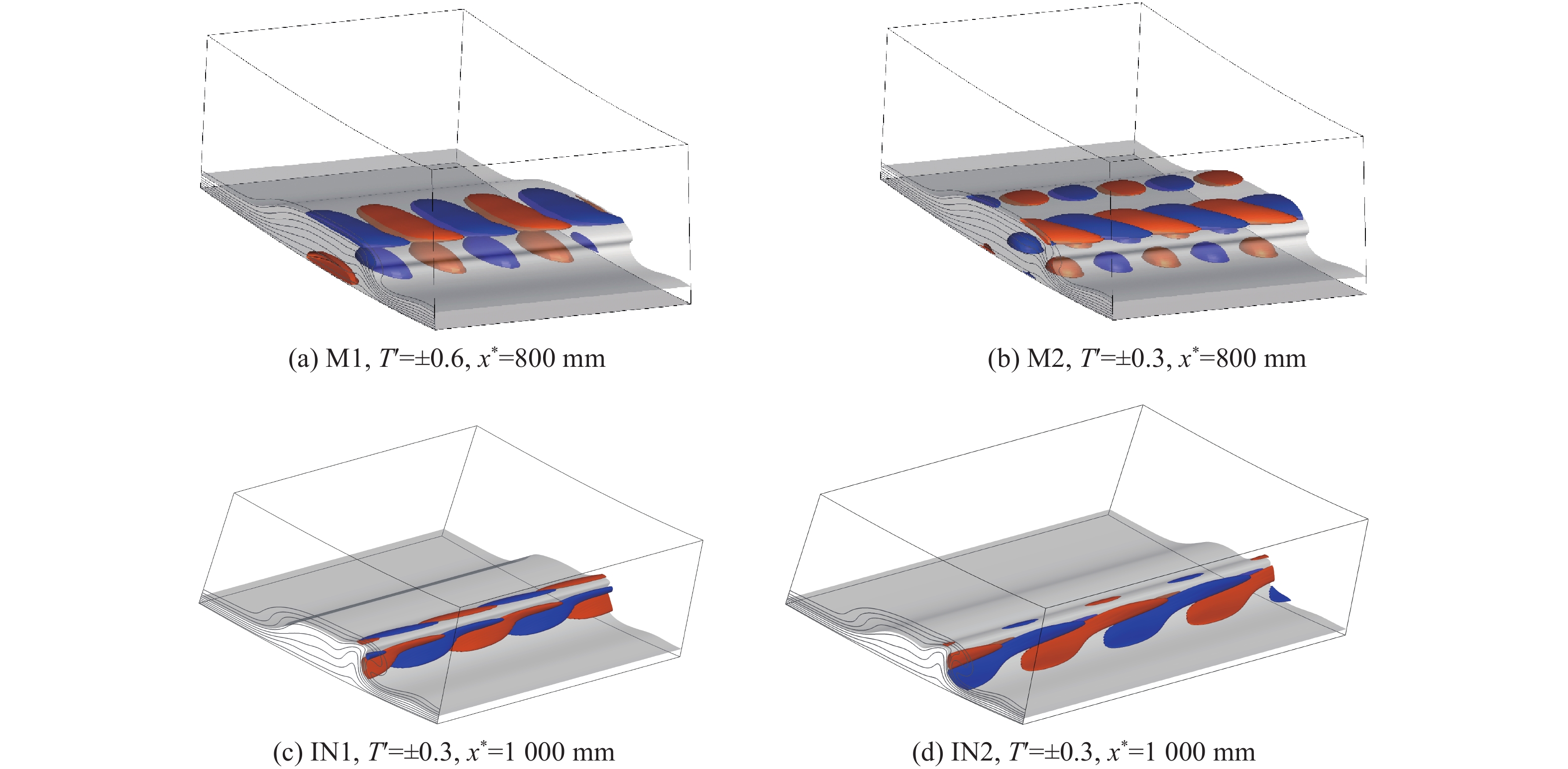
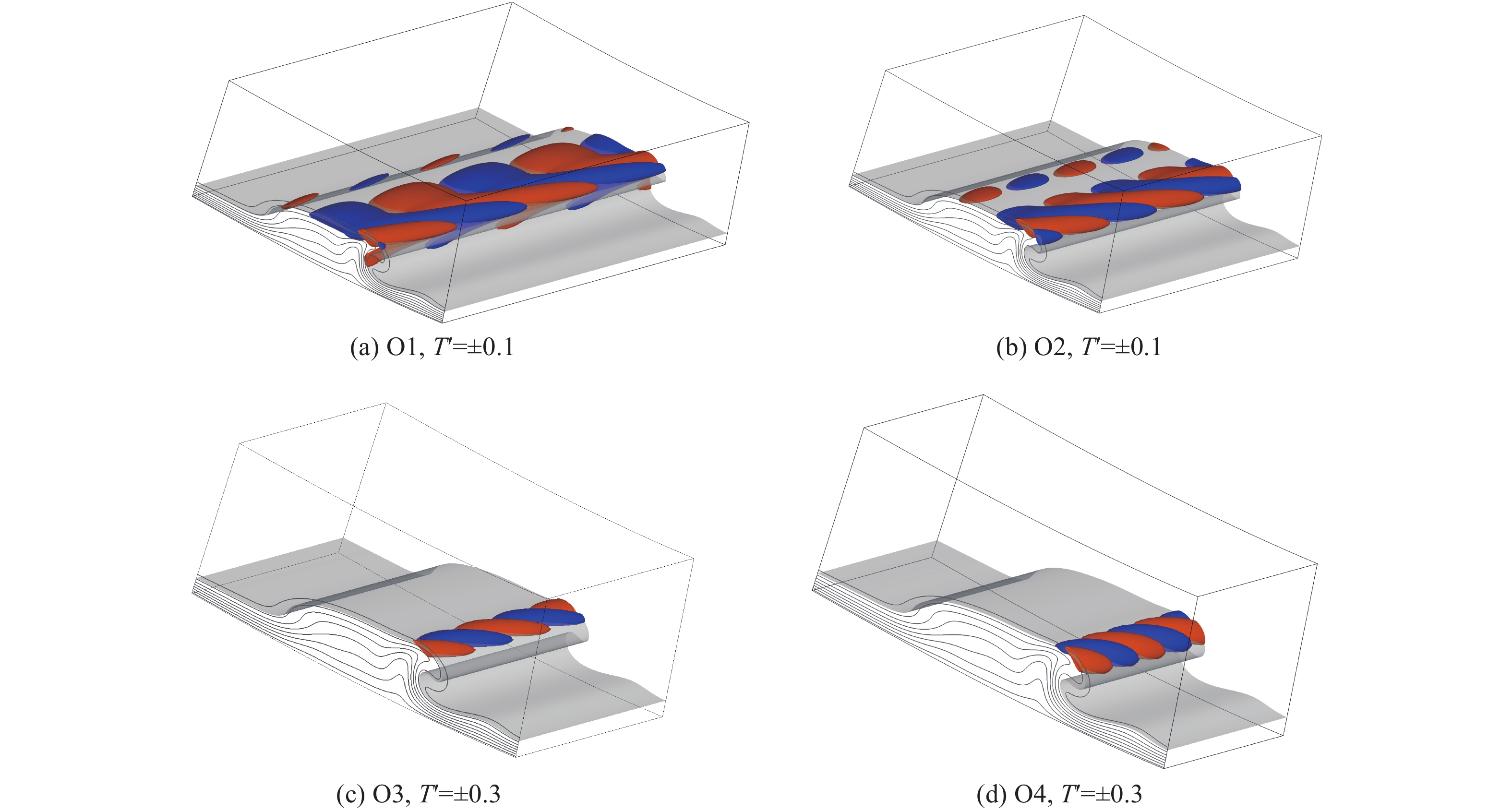
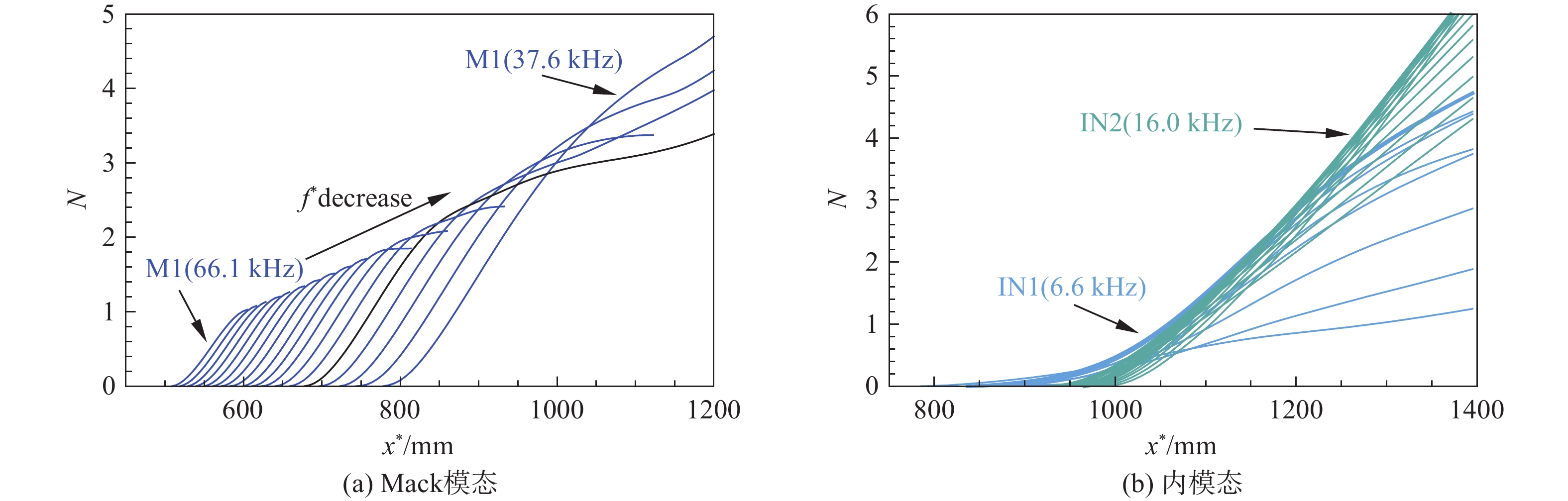
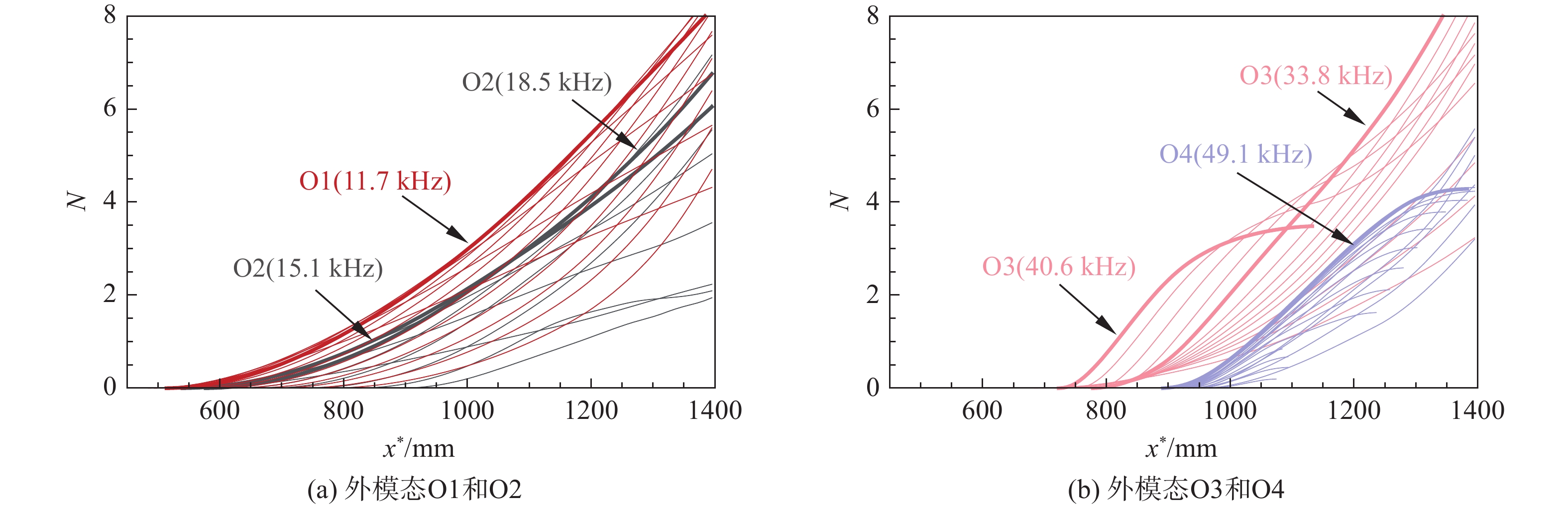
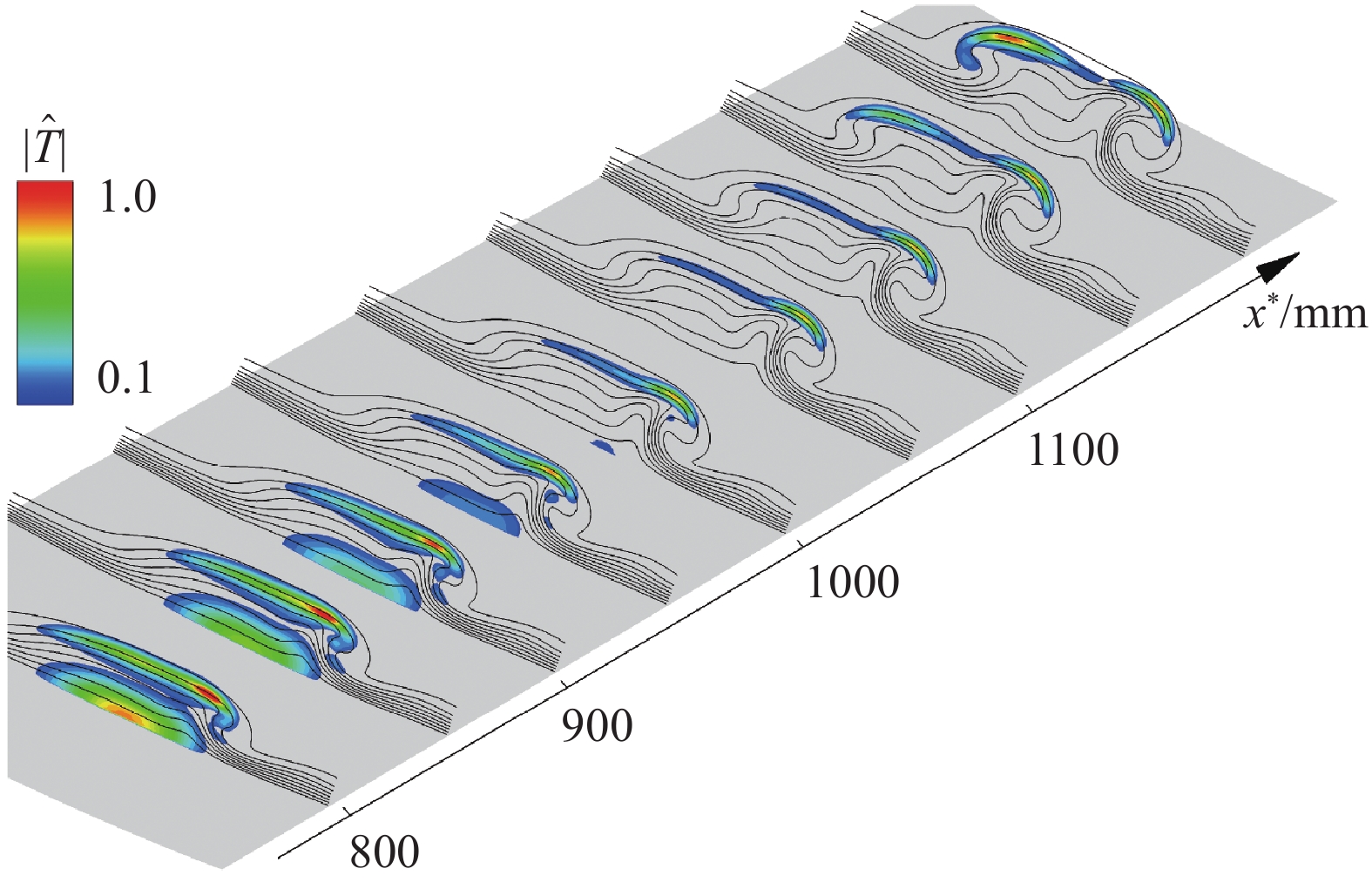
1600 mm，攻角为0º，来流马赫数为6，单位雷诺数为1.0 × 107/m，静温为79 K。采用等温壁面（300 K）条件，通过高阶精度有限差分方法直接求解N-S方程获得层流基本流场。计算结果表明：升力体上表面顶部及下表面长轴处的低速流体向腰部汇聚，形成非对称流向涡，其中靠近下表面一侧的涡卷曲程度更强。稳定性分析结果表明，升力体腰部非对称流向涡的不稳定模态主要有内模态、外模态和Mack模态，内模态主要由展向速度剪切主导，外模态主要由法向速度剪切主导。不同于传统对称流向涡的是，非对称流向涡的扰动形函数主要分布在流向涡卷曲更强的一侧。基于全局稳定性分析的eN方法求解不稳定模态的N值发现：上游Mack模态N值较大，可能在噪声环境下引起转捩；下游外模态N值较大，可能在静声环境下引起转捩。Abstract:The two-dimensional global stability analysis method (BiGlobal) was employed to investigate the instability characteristics of asymmetric streamwise vortex structures at the waist of a hypersonic transition research vehicle (HyTRV), with parameters set as model length 1 600 mm, 0° angle of attack, freestream Mach number 6, unit Reynolds number 1.0×107/m, and static temperature 79 K. The laminar base flow field was obtained through direct numerical simulation by a high-order finite difference method under an isothermal wall condition (300 K). The results indicate that low-velocity fluids near the top of the upper surface and along the long axis of the lower surface converge at the waist, forming streamwise vortices. The pressure gradient disparity between the two sides leads to asymmetric development of these vortices, with the one on the lower side exhibiting more pronounced curling. Stability analysis reveals that the unstable modes of asymmetric streamwise vortices at the lifting body's waist can be categorized into inner modes, outer modes, and Mack modes, aligning with previous research findings. The inner modes are primarily influenced by spanwise velocity shear, whereas the outer modes are predominantly affected by normal velocity shear. The disturbance shape functions are primarily distributed on the side where the streamwise vortex exhibits stronger curling, which is different from the traditional symmetrical streamwise vortex. Utilizing the eN method based on global stability analysis, it is concluded that the N factor of the Mack mode is higher in the upstream region. This suggests that the Mack mode is more likely to initiate transition in a noisy environment. Conversely, the N factor of the outer mode is more pronounced in the downstream region, indicating a higher potential for transition in a quiet environment.
-
Keywords:
- HyTRV /
- lifting body /
- global stability analysis /
- asymmetry streamwise vortex /
- eN
-
![]()
图 4 升力体表面速度云图及壁面极限流线
Figure 4. Velocity contours and wall extremity streamlines of HyTRV
![]()
图 2 不同网格下的流向涡结构对比（流向速度u = 0.05, 0.15, 0.25, …, 0.85）
Figure 2. Comparison of streamwise vortex structure (streamwise velocity) under different grids (u = 0.05, 0.15, 0.25, …, 0.85)
![]()
图 3 稳定性分析网格无关性验证（x*=
1000 mm）Figure 3. Grid independence verification for BiGlobal stability analysis results (x* =
1000 mm)![]()
图 5 x* = 600、800、
1000 、1200 mm典型站位的流向速度等值线（u = 0.05, 0.10, 0.15, …, 0.95）及速度剪切云图Figure 5. Streamwise velocity contours (u = 0.05, 0.10, 0.15, …, 0.95) and velocity shear at selected positions x* = 600, 800,
1000 ,1200 mm![]()
图 6 x* = 600、800、
1000 、1200 mm典型站位的模态增长率和模态相速度随频率变化特征Figure 6. The main unstable modes growth rates and the phase velocities at selected positions x* = 600, 800,
1000 ,1200 mm![]()
图 7 不稳定模态（M1，M2，IN1，IN2）的三维重构（u = 0.05, 0.15, 0.25, …, 0.85）
Figure 7. 3D reconstruction of unstable modes M1, M2, IN1, IN2 (u = 0.05, 0.15, 0.25, …, 0.85)
![]()
图 8 x* = 1000 mm处的不稳定模态（O1，O2，O3，O4）的三维重构（u = 0.05, 0.15, 0.25, …, 0.85）
Figure 8. 3D reconstruction of unstable modes O1, O2, O3, O4 at x* =
1000 mm (u = 0.05, 0.15, 0.25, …, 0.85)![]()
图 9 Mack模态和内模态的N值曲线
Figure 9. N-factors curves of unstable modes: (a) Mack modes, (b) Inner modes
![]()
图 10 外模态O1、O2、O3、O4的N值曲线
Figure 10. N-factors curves of unstable modes: (a) Outer modes O1 and O2, (b) Outer modes O3 and O4
![]()
图 11 不稳定模态在最不稳定频率下的N值曲线
Figure 11. N-factors of unstable modes at their most unstable frequencies
![]()
图 12 频率为39.3 kHz的M1模态在不同站位处的温度扰动形函数
Figure 12. Temperature disturbance shape functions along x* for M1 mode with frequency of 39.3 kHz
-
[1] 陈坚强, 涂国华, 张毅锋, 等 . 高超声速边界层转捩研究现状与发展趋势[J]. 空气动力学学报,2017 ,35 (3 ):311 −337 . doi: 10.7638/kqdlxxb-2017.0030CHEN J Q, TU G H, ZHANG Y F, et al . Hypersnonic boundary layer transition: What we know, where shall we go[J]. Acta Aerodynamica Sinica,2017 ,35 (3 ):311 −337 (in Chinese). doi: 10.7638/kqdlxxb-2017.0030[2] 徐国武, 李锋, 龚安龙, 等 . 非对称转捩对横向偏离稳定的影响[J]. 宇航学报,2015 ,36 (9 ):995 −1001 . doi: 10.3873/j.issn.1000-1328.2015.09.003XU G W, LI F, GONG A L, et al . Effect of asymmetric transition on lateral departure stability[J]. Journal of Astronautics,2015 ,36 (9 ):995 −1001 (in Chinese). doi: 10.3873/j.issn.1000-1328.2015.09.003[3] MACK L M. Special course on stability and transition of laminar flow [M]. AGARD, 1984.
[4] LI X H, ZHANG B, CHEN K, et al . The effects of a smooth hump on the modal linear evolution of streamwise vortices over a yawed cone at Mach 6 from direct numerical simulations[J]. Physics of Fluids,2024 ,36 (1 ):014125 . doi: 10.1063/5.0184861[5] ZHAO L, ZHOU W Q, LI X L, et al . Prediction of transition locations in regions of the minor axis of hypersonic elliptic cones using the BiGlobal-eN method[J]. Advances in Applied Mathematics and Mechanics,2024 ,16 (4 ):805 −832 . doi: 10.4208/aamm.oa-2022-0183[6] PAREDES P, SCHOLTEN A, CHOUDHARI M M, et al . Modal instabilities over blunted cones at angle of attack in hypersonic flow[J]. Journal of Spacecraft and Rockets,2023 ,60 (4 ):1188 −1200 . doi: 10.2514/1.a35590[7] TU G H, CHEN J Q, YUAN X X, et al . Progress in flight tests of hypersonic boundary layer transition[J]. Acta Mechanica Sinica,2021 ,37 (11 ):1589 −1609 . doi: 10.1007/s10409-021-01153-4[8] 陈曦, 陈坚强, 董思卫, 等 . 高超声速6°迎角圆锥边界层背风流向涡稳定性分析[J]. 空气动力学学报,2020 ,38 (2 ):299 −307 . doi: 10.7638/kqdlxxb-2020.0038CHEN X, CHEN J Q, DONG S W, et al . Stability analyses of leeward streamwise vortices for a hypersonic yawed cone at 6 degree angle of attack[J]. Acta Aerodynamica Sinica,2020 ,38 (2 ):299 −307 (in Chinese). doi: 10.7638/kqdlxxb-2020.0038[9] LI X H, CHEN J Q, HUANG Z F, et al . Stability analysis and transition prediction of streamwise vortices over a yawed cone at Mach 6[J]. Physics of Fluids,2020 ,32 (12 ):124110 . doi: 10.1063/5.0031057[10] PAREDES P, GOSSE R, THEOFILIS V, et al . Linear modal instabilities of hypersonic flow over an elliptic cone[J]. Journal of Fluid Mechanics,2016 ,804 :442 −466 . doi: 10.1017/jfm.2016.536[11] CHOUDHARI M, CHANG C L, JENTINK T, et al. Transition analysis for the HIFiRE-5 vehicle[C]// 39th AIAA Fluid Dynamics Conference, San Antonio, Texas. Reston, Virginia: AIAA, 2009.
[12] KOSTAK H E, BOWERSOX R D W . Preflight ground test analyses of the boundary layer transition (BOLT) flight geometry[J]. Journal of Spacecraft and Rockets,2021 ,58 (1 ):67 −77 . doi: 10.2514/1.a34858[13] LI F, CHOUDHARI M, PAREDES P. Transition analysis for isolated trips on BOLT-II wind-tunnel and flight configurations[C]// AIAA AVIATION 2021 FORUM, VIRTUAL EVENT. Reston, Virginia: AIAA, 2021.
[14] 陈坚强, 涂国华, 万兵兵, 等. HyTRV流场特征与边界层稳定性特征分析[J]. 航 空 学 报, 2021, 42(6): 124317. CHEN J Q, TU G H, WAN B B, et al. Characteristics of flow field andboundary-layer stability of HyTRV[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(6): 253−268 (in Chinese).
[15] THEOFILIS V . Global linear instability[J]. Annual Review of Fluid Mechanics,2011 ,43 :319 −352 . doi: 10.1146/annurev-fluid-122109-160705[16] PIERREHUMBERT R T, WISNALL S E . The two- and three-dimensional instabilities of a spatially periodic shear layer[J]. Journal of Fluid Mechanics,1982 ,114 :59 −82 . doi: 10.1017/S0022112082000044[17] LYTTLE I, REED H. Use of transition correlations for three-dimensional boundary layers within hypersonic flows[C]// Fluid Dynamics Conference, San Diego, CA, USA. Reston, Virginia: AIAA, 1995.
[18] KIMMEL R L, KLEIN M A, SCHWOERKE S N . Three-dimensional hypersonic laminar boundary-layer computations for transition experiment design[J]. Journal of Spacecraft and Rockets,1997 ,34 (4 ):409 −415 . doi: 10.2514/2.3236[19] POGGIE J, KIMMEL R L, SCHWOERKE S N . Traveling instability waves in a Mach 8 flow over an elliptic cone[J]. AIAA Journal,2000 ,38 :251 −258 . doi: 10.2514/3.14404[20] PAREDES P, THEOFILIS V . Centerline instabilities on the hypersonic international flight research experimentation HIFiRE-5 elliptic cone model[J]. Journal of Fluids and Structures,2015 ,53 :36 −49 . doi: 10.1016/j.jfluidstructs.2014.11.002[21] PAREDES P, THEOFILIS V. Spatial linear global instability analysis of the HIFiRE-5 elliptic cone model flow[C]// 43rd Fluid Dynamics Conference, San Diego, CA. Reston, Virginia: AIAA, 2013.
[22] CHOUDHARI M M, LI F, PAREDES P. Streak instabilities on HIFiRE-5 elliptic cone[C]// AIAA Scitech 2020 Forum, Orlando, FL. Reston, Virginia: AIAA, 2020.
[23] 李晓虎, 张绍龙, 刘建新, 等 . 高超声速椭圆锥短轴流向涡的二维全局稳定性分析[J]. 空气动力学学报,2018 ,36 (2 ):265 −272 . doi: 10.7638/kqdlxxb-2018.0026LI X H, ZHANG S L, LIU J X, et al . Bi-Global instability of streamwise vortices near minor-axis of hypersonic elliptic cone[J]. Acta Aerodynamica Sinica,2018 ,36 (2 ):265 −272 (in Chinese). doi: 10.7638/kqdlxxb-2018.0026[24] LI X H, YANG Q, CHEN J Q, et al . Effect of three-dimensional smooth humps on hypersonic boundary layer instability of streamwise vortices over a yawed cone[J]. Physics of Fluids,2021 ,33 (6 ):064109 . doi: 10.1063/5.0054396[25] ZHANG B, TU G H, CHEN X, et al . Effects of hump deflection angle on streamwise vortex instability over a yawed cone at Mach 6[J]. Physics of Fluids,2023 ,35 (8 ):084112 . doi: 10.1063/5.0159608[26] ZHANG L, DONG S, LIU S, et al . Stability analysis of streamwise vortices over a blunt inclined cone under a hypersonic flight condition[J]. Physics of Fluids,2022 ,34 :074107 . doi: 10.1063/5.0099952[27] CHEN X, DONG S W, TU G H, et al . Boundary layer transition and linear modal instabilities of hypersonic flow over a lifting body[J]. Journal of Fluid Mechanics,2022 ,938 :A8 . doi: 10.1017/jfm.2021.1125[28] QI H, LI X L, YU C P, et al . Direct numerical simulation of hypersonic boundary layer transition over a lifting-body model HyTRV[J]. Advances in Aerodynamics,2021 ,3 (1 ):31 . doi: 10.1186/s42774-021-00082-x[29] MEN H, LI X, LIU H . Direct numerical simulations of hypersonic boundary layer transition over a hypersonic transition research vehicle model lifting body at different angles of attack[J]. Physics of Fluids,2023 ,35 (4 ):044111 . doi: 10.1063/5.0146651[30] 陈久芬, 徐洋, 蒋万秋, 等 . 升力体外形高超声速边界层转捩红外测量实验[J]. 实验流体力学,2022 ,36 :1 −9 . doi: 10.11729/syltlx20220030CHEN J F, XU Y, JIANG W Q, et al . Infrared thermogram measurement experiment of hypersonic boundary-layer transition of a lifting body[J]. Journal of Experiments in Fluid Mechanics,2022 ,36 :1 −9 (in Chinese). doi: 10.11729/syltlx20220030[31] LIU S S, YUAN X X, LIU Z Y, et al . Design and transition characteristics of a standard model for hypersonic boundary layer transition research[J]. Acta Mechanica Sinica,2021 ,37 (11 ):1637 −1647 . doi: 10.1007/s10409-021-01136-5[32] 李晓虎. 高超声速有攻角锥流向涡的稳定性分析及转捩控制研究[D]. 天津: 天津大学, 2021. LI X H. Stability analysis and transition control of hypersonic cone vortex with angle of attack[D]. Tianjin: Tianjin University, 2021(in Chinese).
[33] SONG R J, ZHAO L, HUANG Z F . Secondary instability of stationary Görtler vortices originating from first/second Mack mode[J]. Physics of Fluids,2020 ,32 (3 ):034109 . doi: 10.1063/1.5140222[34] 张绍龙. 高超声速2: 1椭圆锥边界层的稳定性特征及扰动演化[D]. 天津: 天津大学, 2016. ZHANG S L. Stability characteristics and disturbance evolution of hypersonic 2: 1 elliptic cone boundary layer[D]. Tianjin: Tianjin University, 2016(in Chinese).
[35] 陈曦, 涂国华, 万兵兵, 等 . 基于全局稳定性理论的eN方法对有迎角锥背风流向涡转捩分析[J]. 空气动力学学报,2023 ,42 (1 ):33 −44 . doi: 10.7638/kqdlxxb-2023.0055CHEN X, TU G H, WAN B B, et al . The leeward vortex transition over hypersonic yawed cones by eN method based on global stability theory[J]. Acta Aerodynamica Sinica,2023 ,42 (1 ):33 −44 (in Chinese). doi: 10.7638/kqdlxxb-2023.0055
下载:
计量
- 文章访问数: 58
- HTML全文浏览量: 25
- PDF下载量: 23
